陶瓷体积分数对压电换能器性能影响

李 星,王丽坤,仲 超,张彦军

(北京信息科技大学 北京市传感器重点实验室，北京 100192)

0 引言

水声换能器能将电声信号进行相互转换，被广泛应用在声呐系统中。目前，为了克服目标隐身技术给探测带来的困难，提高对各种目标的探测能力，对换能器的发射功率、灵敏度等各项性能提出了更高的要求；同时，随着水下探测和水声通信的发展，不断地要求增大换能器的探测距离，也要求换能器具有更高的发射电压响应和接收灵敏度。作为水声换能器核心换能材料—压电材料，已被广泛应用于声学换能器[1-2]。1-3型压电复合材料是一种宽频带、高机电耦合系数、低密度及低声阻抗的新型压电材料，现已广泛用于各种高频水声换能器。压电复合材料中压电相材料的体积分数是影响复合材料性能的一个重要因素，许多研究人员已开展了相关的研究。Cunfu He等[3]通过仿真计算了换能器在压电材料体积分数为30%时的激励/接收性能；Vitaly Yu.等[4]研究了陶瓷体积分数对复合材料压电性能的影响，将1-3型无铅复合材料用作压电传感器、水听器；Zhou sheng等[5]对比了体积分数分别为15%和60%的压电换能器，得到体积分数为60%的压电换能器具有更高的灵敏度；孙敏[6]提出压电陶瓷体积分数为40%～60%时，制备的换能器性能较好，但未通过实验去验证；刘鹏[7]通过有限元仿真研究了压电陶瓷体积分数对1-3型压电复合换能器共振频率的影响，随着压电陶瓷体积分数的增加，换能器的前两阶共振频率增大，二者的差值随着压电陶瓷体积分数的增加而增大；轩倩倩[8]研究了高体积分数复合材料的力学性能和热物理性能。由于上述研究缺乏系统性，同时未给出压电陶瓷体积分数与复合材料换能器的发射电压响应、接收灵敏度之间的规律，为此，本文通过有限元分析和实验研究了不同压电陶瓷体积分数(vc)对1-3型压电复合材料换能器收发性能的影响。

1 压电振子的有限元分析

通过压电振子的振动分析可以预测换能器的收发性能。本文采用有限元分析软件ANSYS分析了1-3型压电复合材料振子的振动特性，用以预测换能器的收发性能。首先建立1-3型压电复合材料的实体模型，如图1所示。它由一维连通的压电小柱平行嵌于三维连通的聚合物中构成，其极化方向与压电相小柱厚度方向相同。图中a、b和t分别表示复合材料的长度、宽度和厚度，zw和fw分别表示压电柱的宽度和聚合物的宽度，故复合材料中压电陶瓷体积分数为

(1)

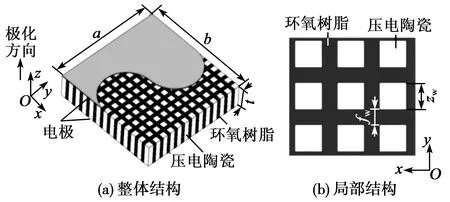
图1 1-3型压电复合材料振子结构

保持zw不变，改变fw，得到vc分别为0.1，0.2，0.3，0.4，0.5，0.7，0.9的7种1-3型压电复合材料。复合材料仿真模型的结构参数如表1所示。

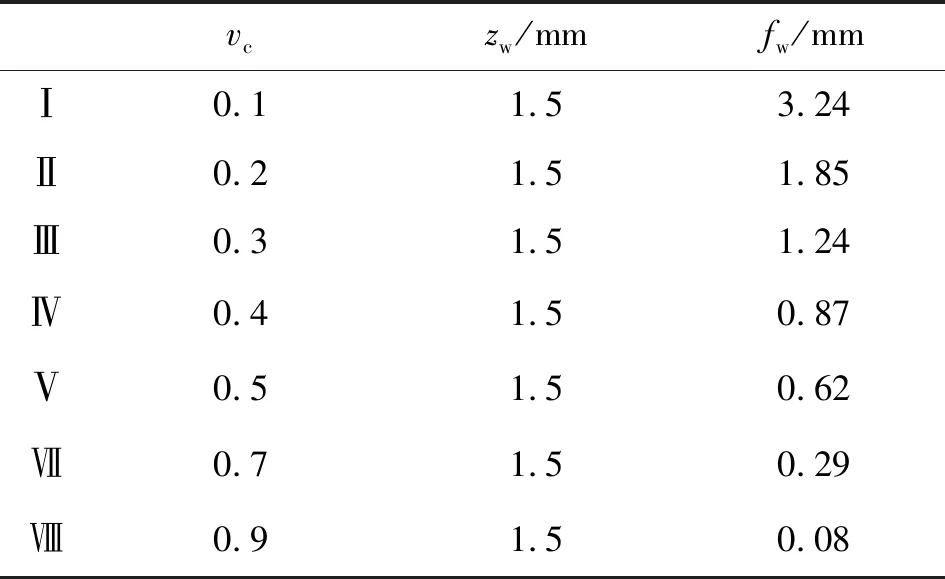
表1 7种复合材料的几何规格

由于1-3型压电复合材料的电极层很薄，建模时可忽略其影响。根据图1所示的结构，利用ANSYS软件建立压电振子的仿真模型，如图2所示。

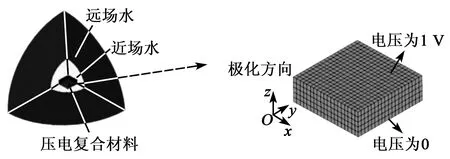
图2 1-3型复合材料压电振子的有限元模型

仿真模型中压电相材料选取PZT-5A。PZT-5A为各向异性材料，单元类型选用三维耦合场固体单元Solid5。聚合物材料为环氧树脂，单元类型为Solid45。

PZT-5A材料密度ρ=7.75×103kg/m3，其刚度矩阵：

1010(N/m2)

(2)

压电常数矩阵：

(3)

介电常数矩阵：

(4)

环氧树脂的密度、杨式模量和泊松比分别为1 050 kg/m3，3.6109N/m2，0.35。

对复合材料的上表面施加电压1 V，下表面施加电压0，扫频范围为200～450 kHz，阻尼系数为0.08。改变模型中的vc(0.1～0.9)，进行谐响应计算，利用后处理器拾取各点的声压，计算振子的发射电压响应和接收灵敏度，结果分别如图3、4所示。

图3 仿真换能器射送电压响应曲线

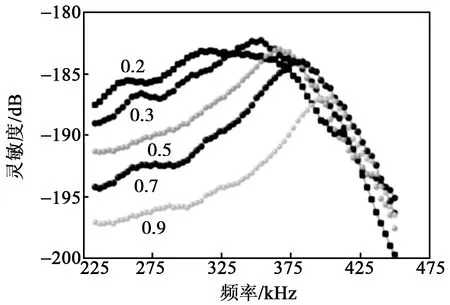
图4 仿真换能器接收灵敏度曲线

由图3可见，换能器的发射电压响应随着vc的增大而增大，当vc=0.5时，发射点电压响应趋于稳定值。由图4可见，当vc=0.2～0.5时，接收灵敏度较高；当vc>0.5时，接收灵敏度逐渐降低。

2 1-3型复合材料及其压电振子的制备

实验中压电陶瓷相选取PZT-5A ，聚合物相选取环氧树脂WSR618，其相关参数分别如表2、3所示。

表2 PZT-5A的相关参数

表3 环氧树脂WSR618的相关参数

本文采用切割填充法研制了1-3型压电复合材料，其制备流程如图5所示。首先按照仿真所选用的结构参数，利用MacroAce 切割机对压电陶瓷沿互相垂直，且都与厚度方向垂直的x，y两个方向进行切割，保留基底，得到5个尺寸均为30 mm×30 mm×7.5 mm、陶瓷柱之间缝隙分别为0.29 mm，0.44 mm，0.87 mm，1.24 mm，1.85 mm的压电陶瓷骨架。各陶瓷骨架四周用胶带粘接，将配好的环氧树脂填充在不同的压电陶瓷骨架中，放入真空箱中抽真空排除气泡，室温固化12 h；将固化好的1-3型复合材料表面进行打磨，去基底，得到厚为5 mm、vc分别为0.2，0.3，0.4，0.6，0.7的压电复合材料。清洁表面，用磁控溅射仪在复合材料表面溅射厚为2 μm的银电极，在1-3型复合材料两电极表面焊接导线，制成各压电振子。1-3压电复合材料的样品实物如图6所示。

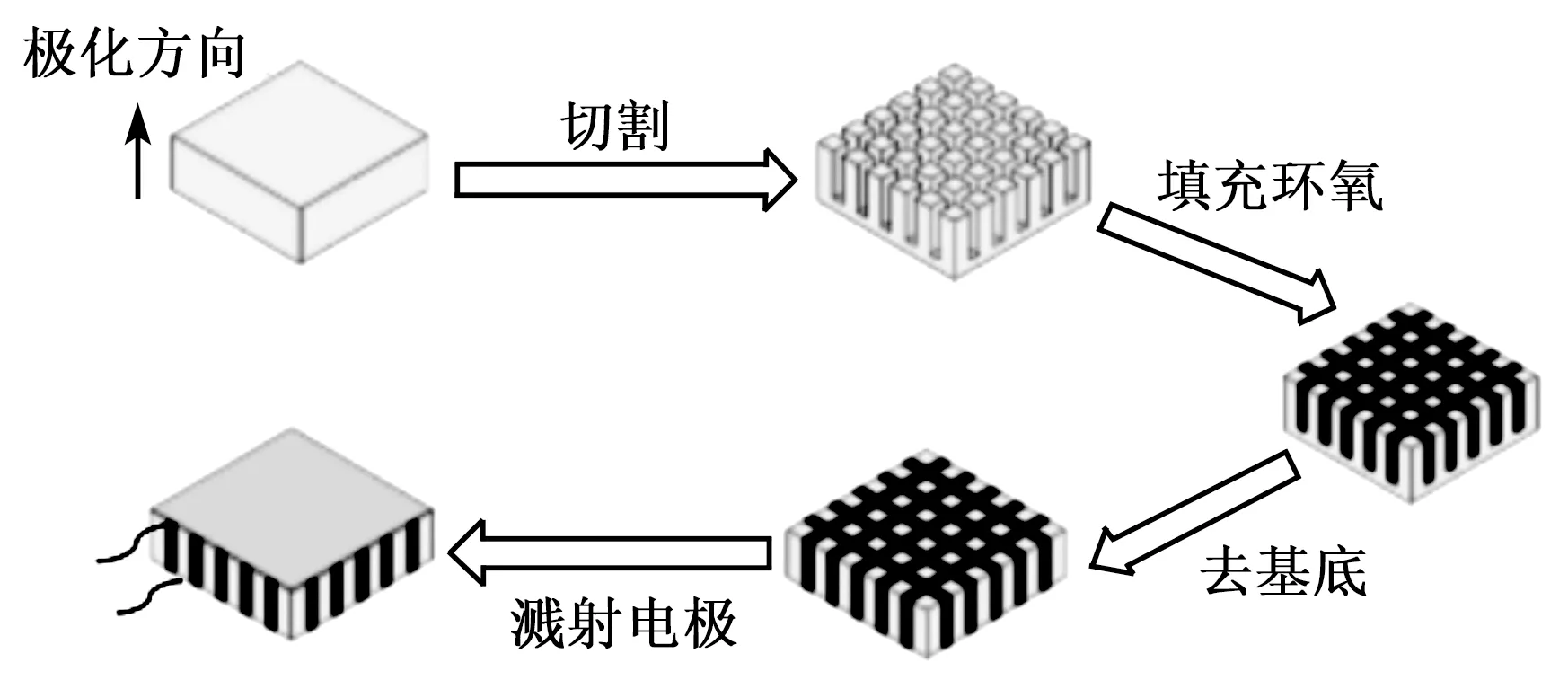
图5 1-3型复合材料及其压电振子的制备流程

图6 1-3型压电复合材料实物

3 1-3型复合材料换能器的制作

应用上述5种压电复合材料制备了水声换能器，其内部结构如图7(a)所示，包括压电复合材料、背衬、防水透声层、前盖板、电缆。其中背衬采用吸声效果较好的硬质泡沫塑料，前盖板采用铝，用环氧树脂将前盖板、背衬、压电复合材料粘接固定，然后将1-3型压电复合材料上焊接的引线连接到输出电缆上，最后将其放入灌注模具中用聚氨酯灌封。图7(b)为灌封后的换能器实物照片，换能器实际尺寸为40 mm×40 mm×25 mm。

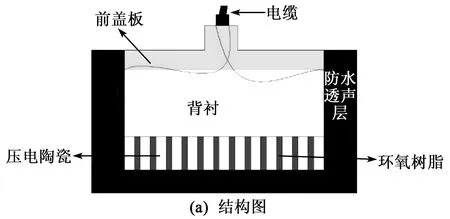
图7 1-3型压电复合材料换能器的结构

根据图7所示的换能器结构制作换能器，制作流程如图8所示。

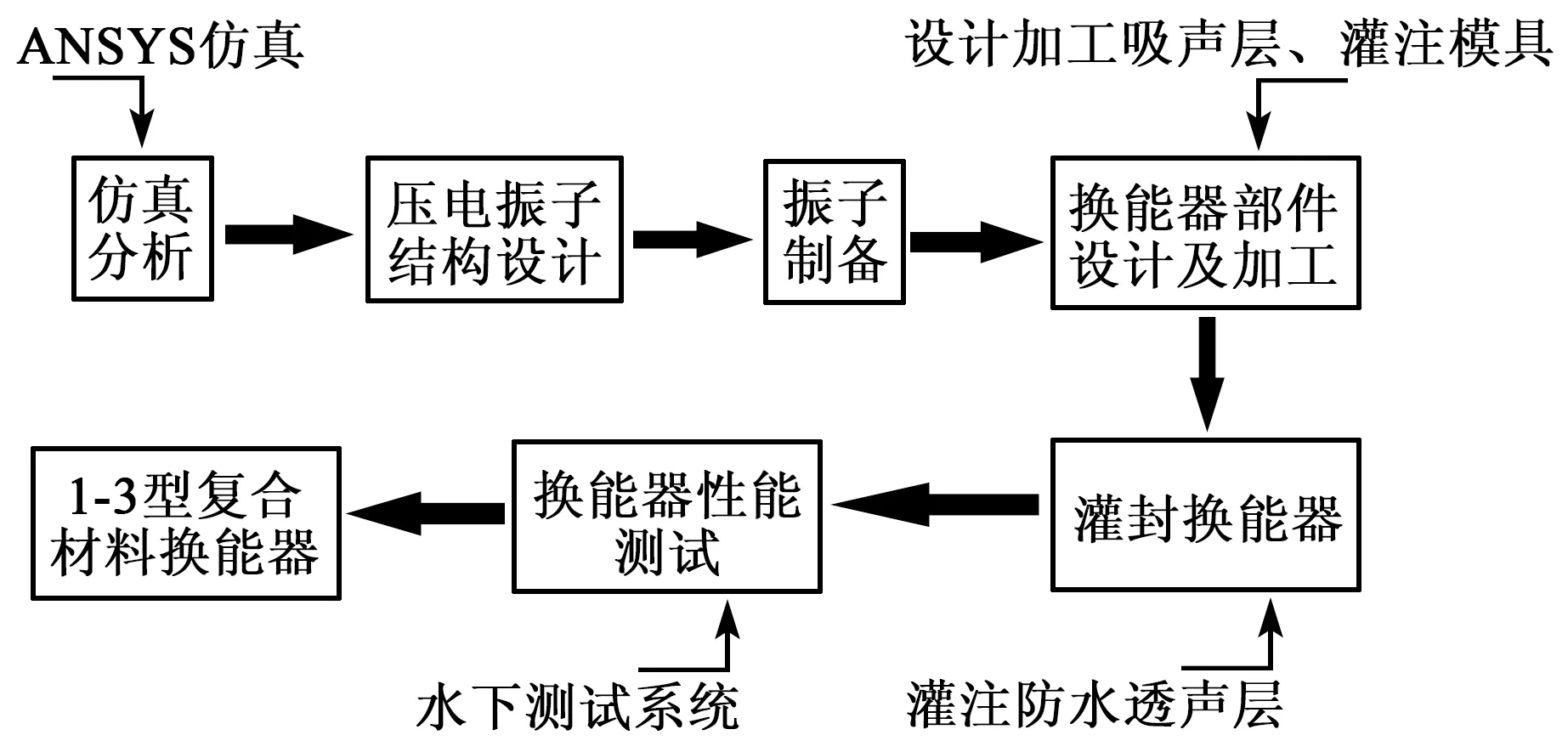
图8 换能器的制作流程

3.1 换能器部件设计

3.1.1 吸声层的设计

本文的压电振子为平面方形结构，故吸声层也设计成边长为30 mm，厚10 mm的平面方形结构，其结构及尺寸如图9所示。吸声层的材料采用硬质泡沫，用以吸收声波，避免声波反射。

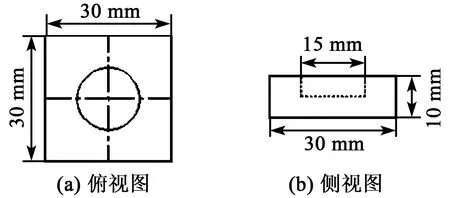
图9 吸声层结构尺寸图

3.1.2 灌注防水透声层模具的设计

为使发射面平整，灌注模具设计为方形，模具材料选用轻质铝。因为铝材料制作的模具表面光滑，能使灌注而成的换能器表面特别是发射面较平滑，换能器的发射性能可以得到有效提升。另外，铝材料的模具导热性较好，有利于聚氨酯材料的固化。模具实物由方形框和下面的底座构成，内部结构尺寸为50 mm×50 mm×40 mm(长×宽×高)，如图10所示。

图10 模具实物

3.2 换能器的制作

将外部线缆与振子各电极引出的导线连接，并将制作好的振子固定在灌注模具的底座上，然后放入模具中，底座与方形框的连接处也用硅橡胶进行密封，防止聚氨酯外溢。振子的发射面与底座垂直，并与模具的侧面平行，该侧面到振子发射面的距离即为计算所得的防水透声层的厚度。防水透声层的厚度一般为λ/4(λ为波长)。波长的计算公式为

(5)

式中：c=1 500 m/s为声波在水中的波速；f为压电振子的串联谐振频率。准备完毕后，制备聚氨酯，并对压电振子进行灌封，制备复合材料压电换能器(见图7(b))。

利用水声测试系统对5个换能器的水中性能分别进行测试。首先将换能器放入消声水池浸泡2 h，再将其安装在水下测试系统的固定位置进行测试。测得换能器的发射电压响应和接收灵敏度的曲线分别如图11、12所示。

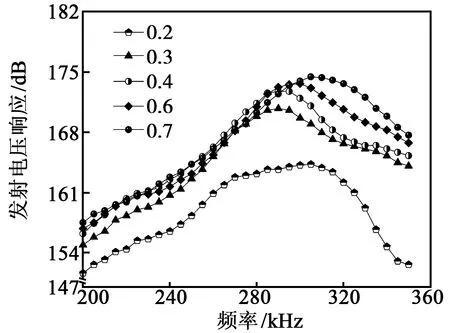
图11 实测换能器发射电压响应曲线

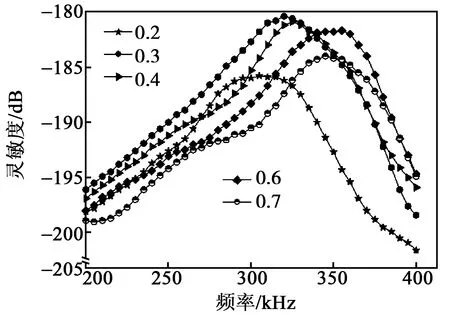
图12 实测换能器接收灵敏度曲线

由图11可见，当vc=0.2～0.4时，换能器的发射电压响应迅速增大；当vc=0.4～0.7时，发射电压响应趋于稳定值173 dB。这是由于随着vc的增大，复合材料的压电常数逐渐增大，压电效应增强，故换能器的发射电压响应逐渐增大。由图12可看出，当vc=0.2～0.4时，换能器的接收灵敏度呈增长趋势；当vc=0.4～0.7时，接收灵敏度逐渐减小，当vc≈0.4时，接收灵敏度达到-180.4 dB。这是由于vc=0.2～0.5时，机电耦合系数逐渐增大；当vc>0.5时，相对介电常数迅速增大，机电耦合系数趋于稳定值，接收灵敏度呈下降趋势。机电耦合系数和相对介电常数曲线如图13所示。

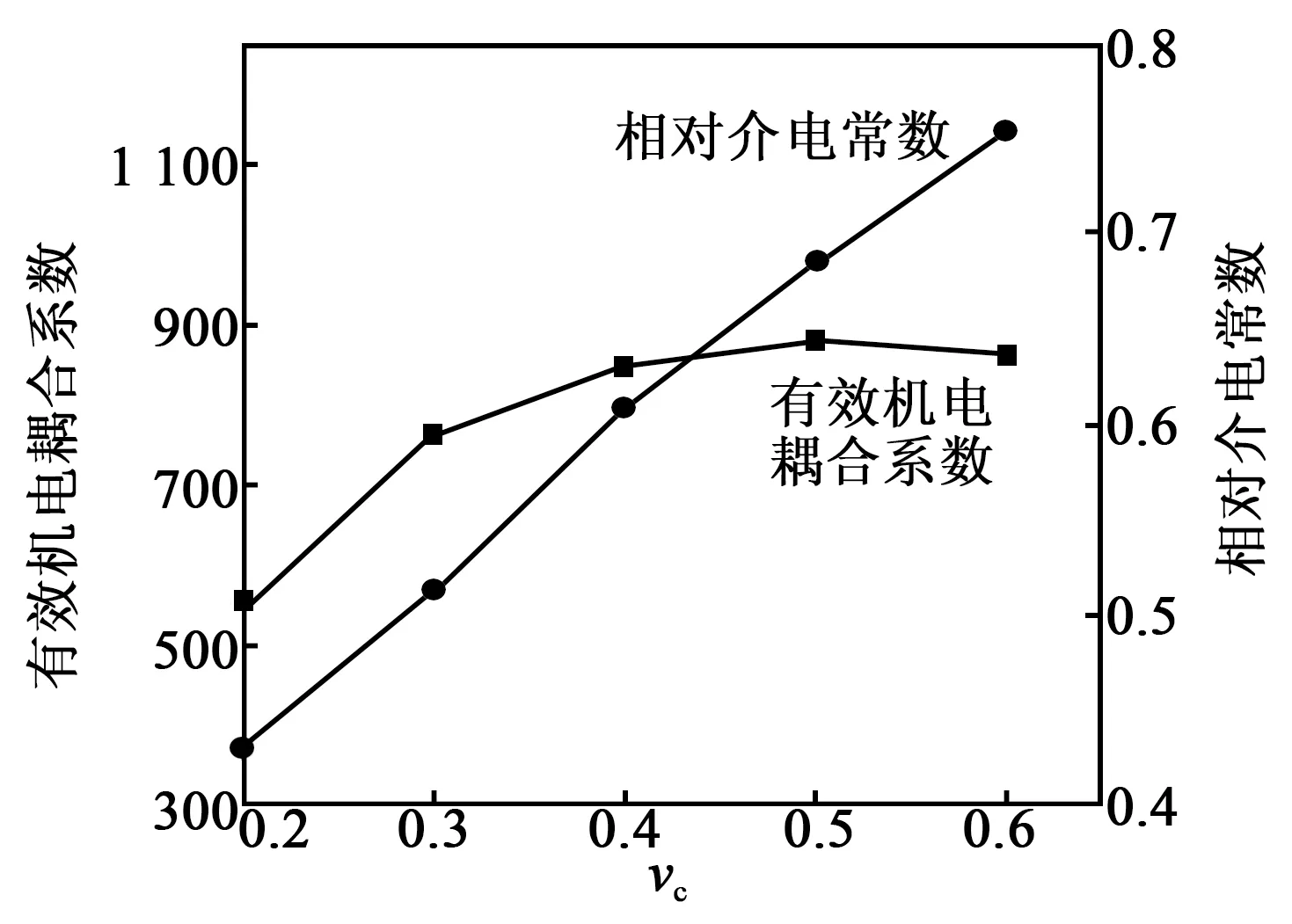
图13 机电耦合系数和相对介电常数虚线图

将第2节仿真的压电振子水中的发射电压响应和接收灵敏度与实验制作的换能器的测试结果进行对比，结果如图14所示。

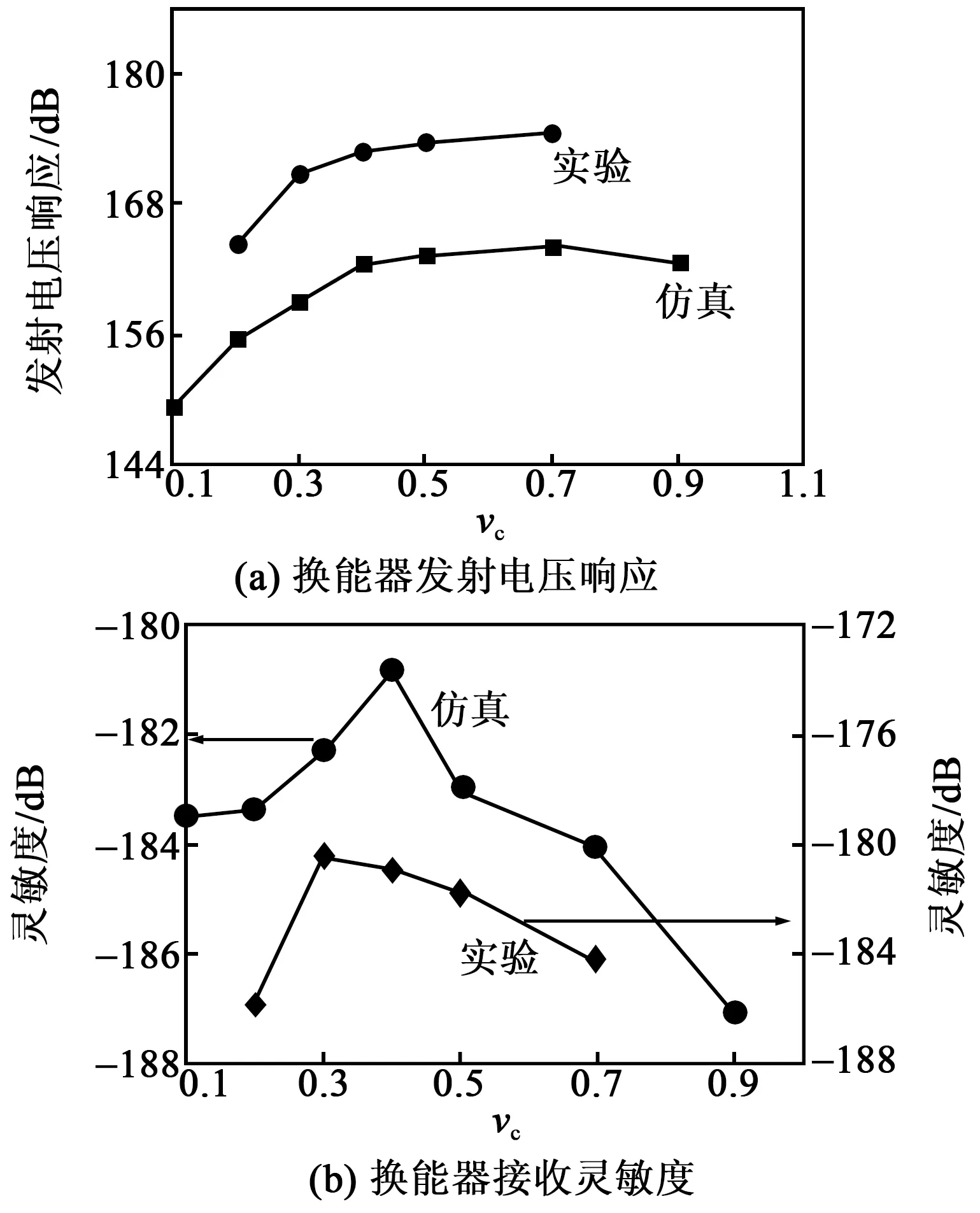
图14 实验与仿真对比图

由图14可见，实验与仿真结果的趋势基本吻合。误差原因是由于仿真中仅对复合材料压电振子模型进行计算，而非换能器整体模型，加之实验制备的复合材料的参数与仿真中的参数存在差异所致。

4 结束语

本文通过仿真和实验分析了压电陶瓷体积分数与1-3型压电复合材料压电换能器的收发性能之间的关系。实验与仿真结果变化趋势基本一致，两者结果均表明,压电换能器谐振点的发射电压响应随着陶瓷体积分数的增加而增大，当陶瓷体积分数在0.4～0.7时，发射电压响应趋于173 dB；当陶瓷体积分数为0.4时，接收灵敏度达到-180.4 dB。

综上分析，复合材料的陶瓷体积分数约为0.4时，1-3型复合材料换能器具有较高的发射电压响应和接收灵敏度，为进一步提高换能器的性能奠定了基础。