直线圆导轨的多次矫直行程预测模型研究
2019-06-25曾玺,凌鹤
曾 玺,凌 鹤
(武汉理工大学 机电工程学院,湖北 武汉 430070)
随着机械装备的高精密化,对组成高精密装备的零件精度要求逐渐提高。金属条材类零件的直线度要求也越来越高,因此国内外学者围绕矫直加工方面展开研究[1]。针对矫直理论,Tsai等[2-3]建立悬臂梁的载荷-挠度模型,推导出不同载荷下的梁弯曲曲线;Elsharkway等[4]研究了T型钢发生拉伸弯曲变形时的拉弯矫直模型;Kosel[5]分析多次纯弯曲时的回弹曲率方程。在国内,翟华等[6]推导出了台阶轴和罗拉轴的矫直行程计算模型;李骏[7]等以矫直过程的3个阶段为基础,建立了轴类零件弯曲时的载荷-挠度模型,并推导出矫直行程计算方程;周磊[8]等以特定使用环境下的T型导轨为研究对象,推导出两个方向维度上的矫直行程解析模型,解决了部分异形截面的矫直行程预测问题。在现有的矫直研究中,虽然矫直理论研究较为成熟,但仅仅重复应用单次矫直计算模型,没有考虑多次矫直过程之间的关系,使得矫直精度无法得到保证,矫直效率低下。实际上单次矫直之间的残余应力的遗传和加载应力之间的叠加关系会对矫直结果产生影响[9-11]。笔者以自主研发的数控精密自动化矫直系统为对象,以单次矫直过程应力变化为依据,以直线圆导轨为研究对象,在弹塑性弯曲的理论基础上,推导建立多次矫直行程预测迭代模型,并通过试验对多次矫直行程预测模型进行验证。
1 矫直方法及理论
选用三点反弯矫直法[12]作为压力矫直方式。压力矫直实际是一个弹塑性反弯的过程。
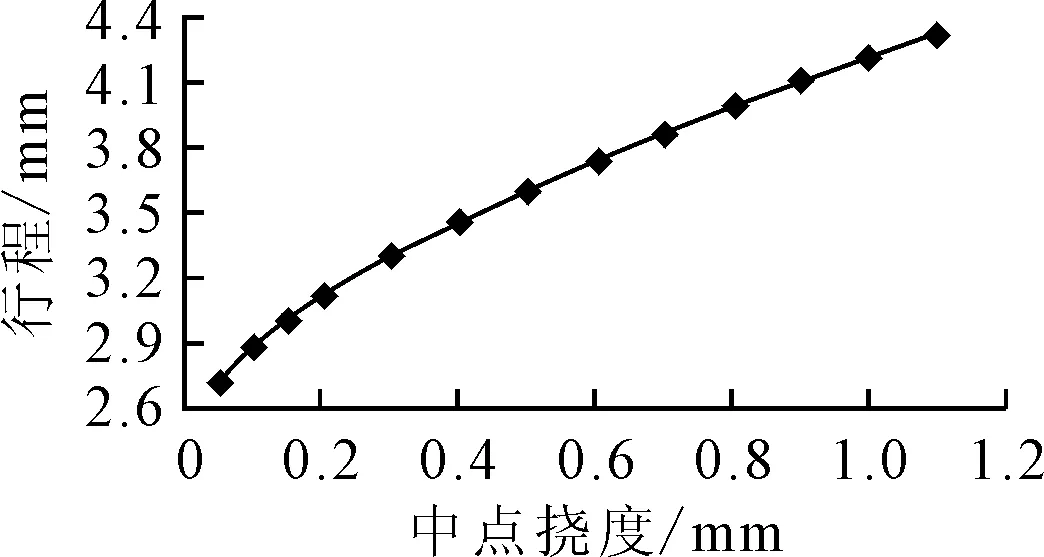
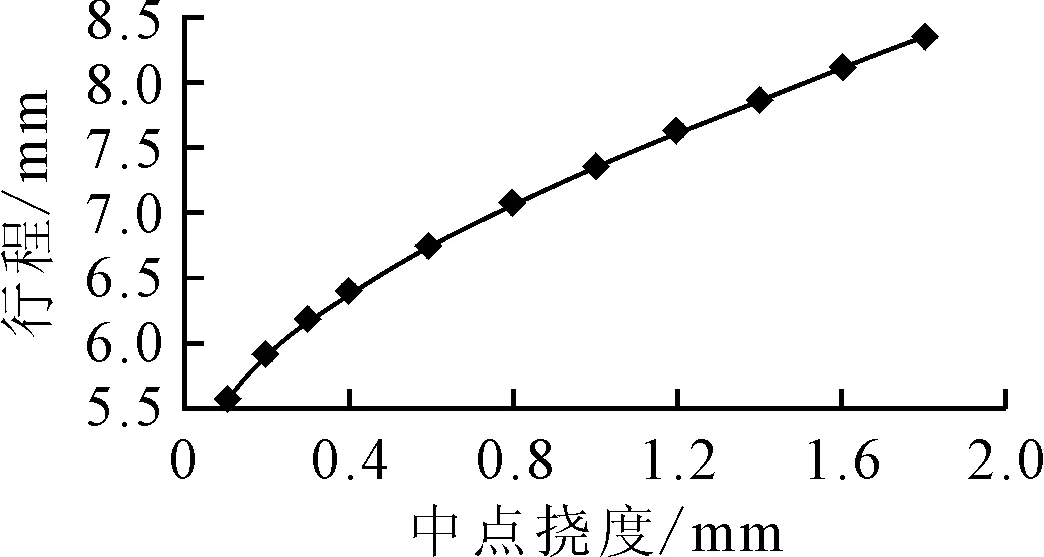
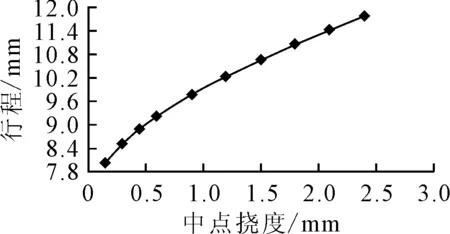
矫直时,选取最大弯曲处为加压点,并将对称的两端作为固定端,使两端简支,假设条材中点处的初始弯曲量为δ0,对加压点处施加相应的集中载荷,工件发生弹塑性变形产生反向弯曲,反弯量为δw;卸载后,条材部分发生塑性变形,剩余部分发生弹性回弹,若此时弹复量与反弯量相等,条材恰好被矫直,即单次矫直的理想状态。若单次矫直未能达到理想状态,需要多次矫直过程,此时残余挠度在直线度范围内则完成矫直,即δc=|δ0-δs| 图1 弯曲应力应变图 因此,截面上的弯矩为: 当σ=σtz/Ht,ξ=Ht/H,Mt=πR3σt/4,整理可得圆截面上的塑弯比为: 由于第一次矫直时,工件不存在残余应力和应变,其应力分布如图2所示。 图2 应力分布图 因此其截面上的矫直加载应力分布方程为: (1) 式中:σ1为第一次矫直时的加载应力;σs为材料的屈服极限;ζ1为第一次矫直时的弹区比;λ为强化系数,λ=E′/E,E为弹性模量;E′为强化模量的平均值;C1为曲率比,C1=1/ζ1。 残余应力是由于加载应力和卸载应力的差异引起的,因此残余应力为: σc=σ-σ′ (2) (3) 式中:σc1为第一次矫直卸载后的残余应力;σH1为第一次矫直的表层应力。 工件的表层发生塑性变形,导致其表层应力发生改变,表层和内部的残余应力方向不同,如图2(b)所示。 在单次矫直中,弹塑性变形阶段中的矫直行程计算过程为: 又因为F=6EI(S-δ)/L3,代入上式可得 (4) 式中:I为截面惯性矩;L为导轨长度;m为塑弯比。 在反复矫直的过程中,下压量是逐渐减小的,因此每次矫直过程中所形成的塑性区域都小于上一次,直到塑性区不存在,即弹区比为1,因此弹区比ζ2>ζ1。 根据应力叠加原理,第二次矫直时的加载应力σp2按线性规律变化,σp2=zC2σs,那么,第二次的实际弯曲应力为σ2=σc1+σp2。 若矫直后,第二次加载应力方向与第一次相反,此时,截面上应力分布函数为: (5) 在弹塑性分界处,根据函数连续性,当z=ζ2时,圆截面上的应力关系应满足: σH1z+ζ2C2σs (6) 式中:ρΣ为总弯曲曲率;ρt为极限弹性曲率,ρΣ2为二次矫直时的总弯曲曲率。 工况弯曲示意图如图3所示,根据图3可知,圆导轨在发生弯曲变形后,其横截面仍然保持为平面,且与变形后的轴线垂直[14],可以得到曲率和挠度之间的关系式: (ρ-R)2=L2+(ρ-R-δ)2 (7) 弯曲变形中工件回弹挠度与弯矩的关系为: δf=ML2/3EI (8) 图3 工件弯曲示意图 在矫直中,总挠度变化量为初始挠度δ0与反弯挠度δw之和,其中包括正反向变化,而反弯挠度等于回弹挠度,总挠度变化量即为矫直行程。将前面计算所得关系式代入可得二次矫直的行程S2为: (9) 根据上述计算两次矫直的过程,进行多次矫直迭代计算。 假设第i-1次矫直后,截面上的残余应力为σc(i-1),那么第i次矫直时的加载应力为σpi,那么截面上的实际弯曲应力为: σi=σc(i-1)+σpi (10) 其中,σpi=zCiσs。 由单次矫直和二次矫直的公式可知,在多次矫直中,分段函数里,第一段和最后一段只与弹区比有关,其余段和前一次矫直中的首项符号有关,也是前期矫直所产生影响的叠加。且在分段函数中可以观察出,以中性层为分界面,除了第一段和最后一段,其余部分均是对称分布,即上下层为相反关系。因此,可推导出通项公式。 因此,当矫直次数i≥2时,截面上的应力分布函数为: 则残余应力的表达式为: (11) 根据前面单次矫直和二次矫直的过程,可得在多次矫直中的矫直行程迭代模型为: (12) 式(12)为隐式推导公式,其精确度由前期实际迭代情况而定,并不断由迭代过程进行修正。 根据矫直行程预测模型,并代入材料的各项具体数据,利用MATLAB进行理论计算,针对不同的初始挠度计算出结果,得到不同跨矩下的挠度-矫直行程分布图,如图4~图6所示。 图4 跨距350 mm挠度-矫直行程分布图 图5 跨距500 mm挠度-矫直行程分布图 图6 跨距600 mm挠度-矫直行程分布图 采用有限单元法[15],结合弹塑性有限元分析,通过创建有限元模型,设置好模型的各项参数,针对不同挠度的导轨,依据矫直预测模型计算出矫直行程,利用Ansys Workbench对导轨进行模拟加载,并进行各项数据的求解。 设定工件直径为16 mm,弹性阶段选用Isotropic Elasticity模型,塑性阶段选择BKIN模型。选用swept方式对工件进行网格划分,约束其两端面的自由度,释放绕Z轴的转动和右端面的移动。选用点载荷的方式对导轨进行加载。整个矫直过程分为加载和卸载两个部分,在不同初始挠度的条件下,设定相应的加载参数,加载完成后随即卸载,得到不同跨矩下的挠度矫直行程分布图,如图7~图9所示。应力变化情况如图10所示。 图7 跨距350 mm挠度-矫直行程分布图 图8 跨距500 mm挠度-矫直行程分布图 图9 跨距600 mm挠度-矫直行程分布图 图10 应力变化图 由图10可知,随着矫直过程的时间增加,工件挠度减小,残余应力也逐渐减小。 矫直试验采用三点反弯矫直的方法进行,利用自主研发的精密数控矫直机进行在线矫直试验,采用搭载于矫直机的位移传感器进行在线测量加载点的挠度值。 选用直径为16 mm,长度为350、500、600 mm的圆导轨各1根,材料为45号钢,分为3个实验组。具体参数如表1所示。 表1 直线导轨参数表 将圆导轨分别标号为1、2、3,按顺序依次对3组导轨进行初始挠度的测量,并代入到多次矫直行程模型中,计算出相应的矫直行程,待到应力释放后测量导轨的残余挠度;再根据残余挠度继续进行迭代计算,再次得出矫直行程,在直线导轨上完成相应矫直步骤;重复上述过程,直至残余挠度控制在直线度要求之内。 经过3组试验,得到试验结果,如表2所示。 表2 试验数据 试验中,矫直样件采用相同材料的直线导轨,针对多次矫直行程模型进行矫直试验。对3组对比组试验结果进行分析可知,在多次矫直过程中残余挠度值趋于收敛,即直线度误差逐渐减小,说明了行程预测模型的正确性;在同样长度和截面参数相同的情况下,影响矫直次数和矫直效果的主要因素是矫直对象的初始挠度。 针对直线圆导轨的多次矫直行程预测模型,分析了直线圆导轨在多次弹塑性变形过程中,圆截面上应力变化及挠度变化的规律,推导出多次弯曲矫直时圆导轨挠度与矫直行程的迭代关系式,并进行了有限元分析。以材料为45号钢的直线圆导轨为试验对象,进行模型的理论验证和试验验证,得出以下结论: (1)直线圆导轨在经历多次弯曲矫直的过程中,其圆截面上存在叠加的加载应力与残余应力。将上一次弯曲矫直后所产生的残余应力作为预应力,得出多次矫直过程的行程预测公式; (2)通过试验验证可知,利用所推导出的行程预测模型,将直线圆导轨进行多次矫直后,得到了较好的矫直结果,更接近导轨的直线度要求,相较于单次矫直结果,证明了多次矫直行程预测模型的正确性。2 矫直行程模型建立
2.1 单次矫直行程模型
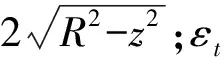

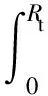
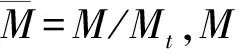
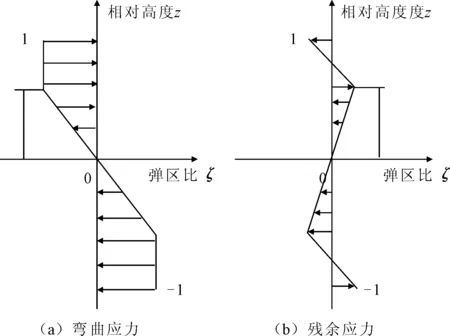
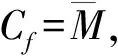
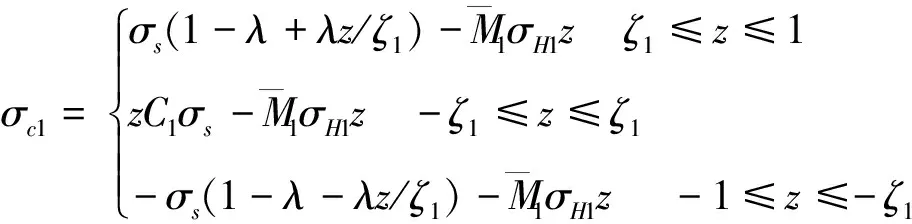
2.2 二次矫直
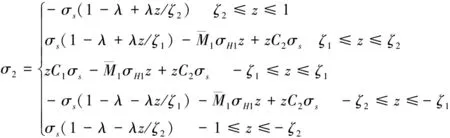
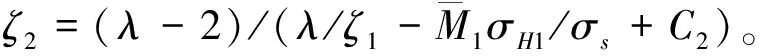
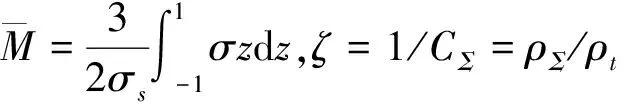

2.3 多次矫直
3 仿真与试验
3.1 理论计算
3.2 仿真结果

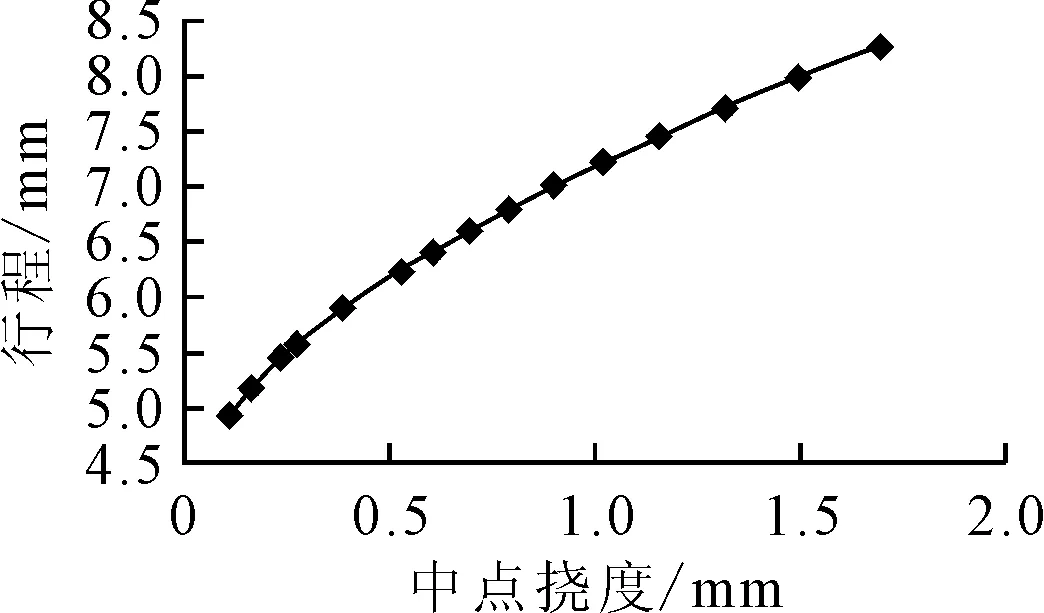
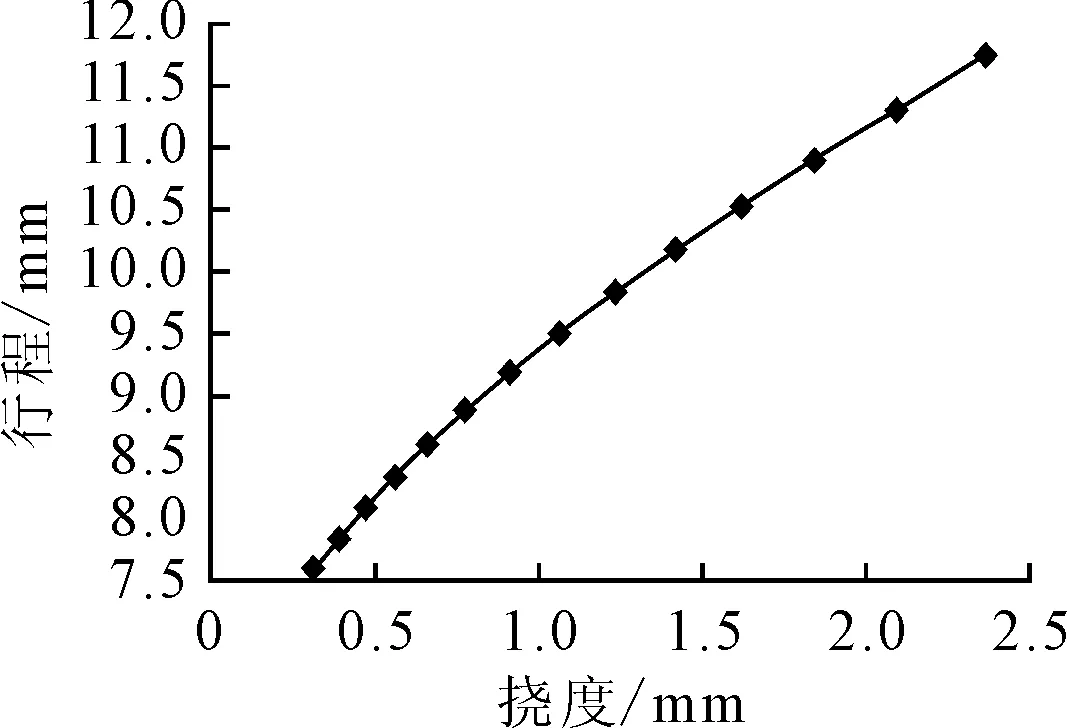
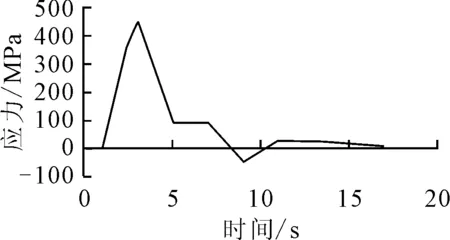
3.3 试验过程
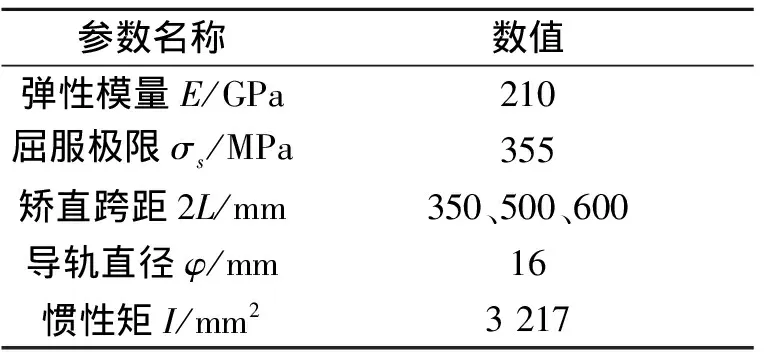
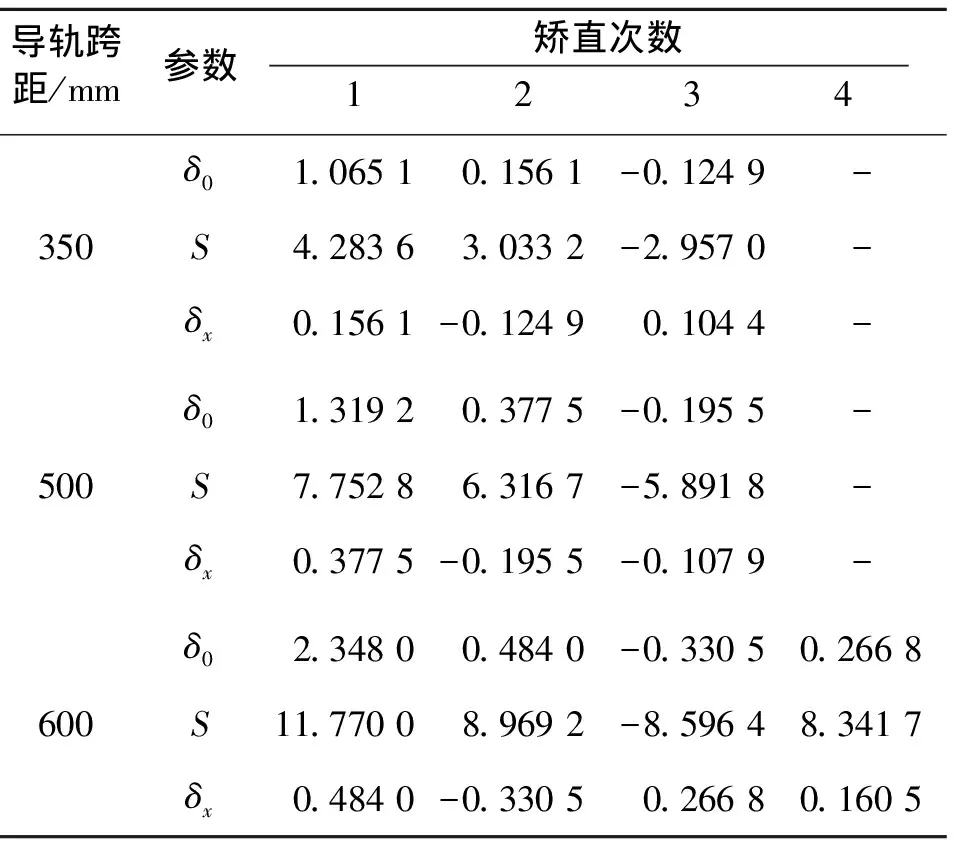
3.4 试验结果分析
4 结论
