射频接收机中自动增益控制电路建模与设计

王 帅，张 杰，张彦峰

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

在无线通信中，由于受距离远近、电磁波辐射功率大小及气象条件等各种因素影响，射频接收机接收到的射频信号功率强度动态范围较大。为了保证接收机输出信号强度和信号质量，接收机需要AGC电路[1-2]。

在实际电路应用中，一般要求AGC电路的增益调整时间恒定，与接收到的信号功率大小无关，与设置的稳定输出功率值无关。同时，时分通信体制要求射频接收机具有较小的AGC稳定时间，而QPSK等信号调制体制要求射频接收机具有较大的AGC稳定时间[3-5]。因此，AGC电路增益调整时间的长短十分关键。

1 AGC环路分析

射频接收机兼容QPSK和时分体制，要求该接收机AGC稳定时间(AGC时间常数是稳定到63.2%所需时间，AGC稳定时间一般是几倍的时间常数)在35～40 μs，传统的设计方法是根据经验值进行初值电装，再根据测试结果不断修正再测试，拓扑结构不合适则需要重新投板再加工，缺乏准确的理论设计和仿真设计。

典型的AGC电路原理框图如图1所示，一般由可变增益放大器(VGA)、检波器、比较电路和环路滤波电路组成[6-7]。检波电压经过与基准电压的比较和环路滤波，产生的控制电压调整可变增益放大器增益，使输出信号电平在较小的范围内波动。

图1 AGC电路原理框图

AGC电路的优点是具有优秀的线性特性且电路实现不需要大动态范围的检波器；缺点是存在一定的不稳定性，即为了保持稳定性限定了最大的环路滤波带宽，限定的最大环路滤波带宽限制了最小的AGC电路时间常数。Vout和Vin分别是输入输出信号的幅度，G(Vc)是受电压Vc控制的可变增益放大器增益[8]，则:

Vout=Vin·G(Vc)。

(1)

y(t)=x(t)+ln(G(Vc))。

(2)

图2 自动增益控制环路模型

可变增益放大器的增益控制电压为：

(3)

对式(2)两边求导，并把式(3)代入，得到:

(4)

假如L(s)和比较电路用图3所示电路来实现，本文称其为RC比较环路滤波电路。

图3 RC比较环路滤波电路

根据图3可以推导出：

(5)

结合式(3)～式(5)得到：

(6)

(7)

时间常数为：

(8)

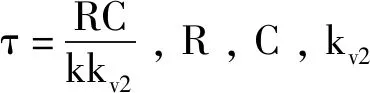
G(Vc)=k1ekVc，

(9)

式中，k1为常数，所以要求可变增益放大器的增益与控制电压成指数关系，即增益的对数跟控制电压成线性关系，可以实现AGC时间常数恒定的要求[10-11]。

2 AGC电路建模

根据上节论述得到了AGC电路恒定时间常数的要求，但仍然缺少复杂AGC电路时间常数的详细公式，没有解决特定AGC时间常数的设计难题。本文对实际射频接收机AGC电路进行建模，模型如图4所示。

该模型不同于图2的模型，图2的模型是基于电压进行建模运算，虽然进行了对数转换，但仍然不够直观。图4的模型直接采用实际接收机接收功率进行建模运算[12-14]，该模型的Pin，Pout分别代表AGC电路的输入功率和输出功率，量值为dBm；GdB(Vc)表示可变增益放大器的增益与控制电压的对数关系，表达式为GdB(Vc)=kg·Vc，kg是可变增益放大器对数增益与控制电压的线性斜率，单位为dB/V,该可变增益放大器的特性符合上节的AGC电路恒定时间常数的限定要求。D(Pout)表征检波电压与输出功率成对数关系，表达式为D(Pout)=kd·Pout，kd是检波器电压与输出功率的线性斜率，单位为V/dBm。H(s)和C(s)表征AGC电路中比较和环路滤波电路的实际数学建模。因此得到式(10)～式(13)。

图4 射频接收机AGC电路模型

(10)

Vc=H(s)Vdec+C(s)Vref，

(11)

Pout=Pin+kg(kdH(s)Pout+C(s)Vref)，

(12)

(13)

(14)

(15)

根据式(13)可知，Pout为Pin和Vref经过各自闭环传递函数线性叠加的结果，即式(14)～式(15)。对于一个实际AGC电路，Vref为固定值，根据上一节知道，图4配置模型的AGC时间常数与Vref无关。因此对于图4模型的AGC时间常数只需要分析式(14)，而式(15)影响最后的收敛稳定值。

(16)

根据式(14)得到Pout1的闭环传递函数为：

(17)

图4类型的AGC电路时间常数为式(18)，与式(8)相吻合。

(18)

根据式(18)可知图4类型的AGC电路时间常数与该电路的电容C容值、电阻R阻值成正比，与可变增益放大器增益斜率和检波斜率成反比。

当一个AGC电路可变增益放大器和检波芯片已经确定，则影响AGC时间常数的主要因素就是比较环路滤波电路。下面针对另外2种射频接收机常用的AGC电路进行AGC时间常数公式推导，图5是一种较为常用的比较环路滤波电路(本文称为常用一阶比较环路滤波电路)，对该电路采用本文论述的方法进行分析，得到闭环传递函数式(19)，该拓扑结构的时间常数公式为式(20)，根据公式知道AGC电路的时间常数与电容容值成正比，与R1和R2阻值正相关，与可变增益放大器增益斜率和检波斜率成反相关。

图5 常用一阶比较环路滤波电路

(19)

(20)

(21)

(22)

(23)

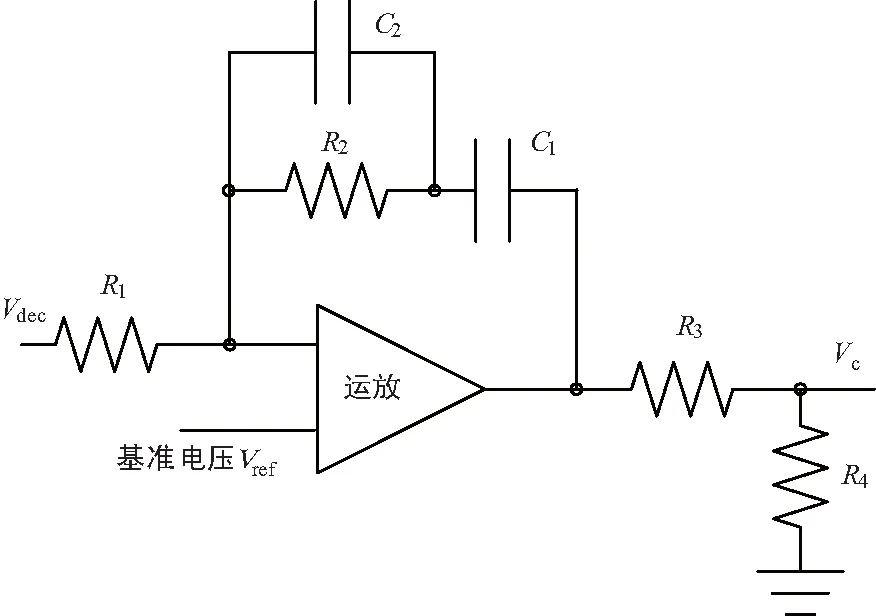
图6 常用二阶比较环路滤波电路

3 仿真验证和电路验证

上节对射频接收机的AGC电路进行了具体建模，对3种常见的比较环路滤波电路进行了AGC时间常数公式推导，得到了具体的表达式。本节采用电子设计软件进行建模仿真，仿真结果与上节的公式结论进行对比验证，对常用二阶比较环路滤波电路进行加工制作，测试其AGC稳定时间。

采用Keysight公司的Advanced Design System(ADS)软件对接收机的AGC电路进行建模仿真，仿真原理图如图7所示，该仿真针对的是RC比较环路滤波电路[15]。模型中采用两级可变增益放大器来保证AGC电路的动态范围，增益斜率为100 dB/V，检波器的检波斜率为0.05 V/dB,在原理图中对AMP6的VoltSlope参数进行了合适设置使其匹配实际检波器斜率[16-18]。因此kg=100 dB/V，kd=0.05 V/dB，R=40 kΩ，C=100 nF，根据式(18)计算得到时间常数为0.8 ms(稳定到63.2%)，假设稳定到86.5%为整个AGC电路的稳定时间，那么稳定时间为2倍时间常数，即为1.6 ms。ADS仿真结果如图8所示，根据仿真数据分析得到向下恢复时间常数为0.809 ms，稳定时间为1.617 ms；向上恢复时间常数为0.807 ms，稳定时间为1.616 ms;与模型公式理论计算结果吻合很好。

图7 ADS软件下AGC电路仿真原理图

对图5模型(常用一阶比较环路滤波电路)进行ADS软件仿真，可变增益放大器参数和检波器参数同图7一致，其他参数为R1=39 kΩ，R2=30 kΩ，C=100 nF；图6模型(常用二阶比较环路滤波电路)相应参数为R1=10 kΩ，R2=10 kΩ，R3=39 kΩ，R4=10 kΩ，C1=1 nF，C2=16 pF。按照式(20)可以计算出常用一阶比较环路滤波电路模型在该参数下的时间常数为3.78 ms；而采用ADS软件对其进行仿真得到下降恢复时间常数为3.82 ms，上升恢复时间常数为3.74 ms。按照式(23)计算出常用二阶比较环路滤波电路模型在该参数下无阻尼自然振荡角频率为790 570 rad/s,阻尼系数为7.97。因为阻尼系数大于1，该拓扑为过阻尼，极点

闭环极点p2比p1距虚轴远得多，故忽略p2对输出的影响，把二阶系统近似作为一阶系统来处理，因此，时间常数计算为τ3=-1/p1=20 μs；采用ADS软件对其电路结构进行仿真，得到下降恢复时间常数为19 μs，上升恢复时间常数为19 μs。3种电路结构模型理论计算和ADS软件仿真结果对比如表1所示。

表1 AGC时间常数理论计算和ADS仿真对比

拓扑类型理论计算时间常数ADS仿真下降恢复时间常数ADS仿真上升恢复时间常数图3拓扑(RC比较环路滤波电路)0.800ms0.809ms0.807ms图5拓扑(常用一阶比较环路滤波电路)3.780ms3.820ms3.740ms图6拓扑(常用二阶比较环路滤波电路)20.00μs19.00μs19.00μs

该射频接收机实际要求AGC稳定时间为35～40 μs，采用常用二阶比较环路滤波电路的拓扑结构和举例的各个电阻和电容参数进行实际电路制作，图9为加工电装后的实际电路，该电路的AGC时间常数理论计算为20 μs，ADS仿真结果为19 μs，各自达到稳定时间(86.5%稳定)分别为40,38 μs。实际测试结果如图10所示，AGC稳定时间为36.8 μs，与理论计算和软件仿真结果吻合良好，满足实际系统要求。

图9 接收机中的AGC电路

图10 示波器测试结果

4 结束语

本文对射频接收机中自动增益控制电路进行了建模分析，得到了稳定时间常数的电路条件。在此基础上提出了射频接收机中自动增益控制电路的物理模型，对于3种常见自动增益控制电路进行了时间常数公式推导和ADS电子设计软件仿真验证，而且进行了实际射频接收机电路制作和测试，理论计算结果、软件仿真结果和实际电路测试结果吻合良好，证明了模型的准确性和软件仿真的可行性。对于特定AGC时间常数的自动增益控制电路设计，采用本文的公式和方法可以准确计算出该AGC电路的时间常数，利用ADS电子设计软件继续对电路参数进行仿真优化直到满足系统需求的AGC时间，节约了后期大量的调试时间，本文的设计方法对AGC电路设计有很好的理论指导作用。