非圆形隧洞收敛-约束特征曲线的数值求解方法
2019-06-24周辉郑俊张传庆胡大伟高阳杨凡杰
周辉 郑俊 张传庆 胡大伟 高阳 杨凡杰
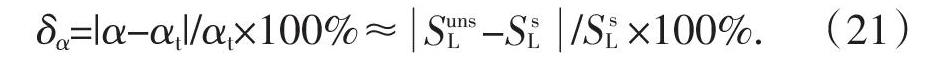
摘 要:利用应力释放法原理,在收敛-约束解析法基础上,提出了适合任意断面隧洞的收敛-约束特征曲线数值求解方法,通过与收敛-约束解析法对比验证该方法的有效性,并与常用的数值方法进行对比,最后对收敛-约束特征曲线数值求解方法的计算误差进行分析.研究结果表明:收敛-约束特征曲线数值求解方法适合非圆形隧洞,由于通过施加节点支撑反力实现应力释放,该方法同样适合应力状态复杂的隧洞;以滇中引水工程为例,将收敛-约束特征曲线数值求解方法与收敛-约束解析法的计算结果进行对比,验证了收敛-约束特征曲线数值求解方法的有效性;收敛-约束特征曲线数值求解方法计算结果存在一定的误差,其整体相对误差小于10%.收敛-约束特征曲线数值求解方法的适用性更加广泛,可为隧洞工程的初期支护优化设计及安全性评价提供参考,具有一定的工程应用价值.
关键词:收敛-约束法;隧洞;应力释放法;围岩特征曲线;不平衡力;应力分布
中图分类号:TV6 文献标志码:A
Abstract: By using the principle of stress release method, a numerical solution method of convergence-confinement characteristic curve was proposed for tunnels with various cross-sections based on the convergence-confinement analysis method. The validity of the proposed method was verified by comparison with the convergence-confinement analytical method, and compared with the usual numerical methods. Finally, the calculation error of the numerical solution method for convergence-confinement characteristic curve was analyzed. The results show that the numerical solution method of convergence-confinement characteristic curve is suitable for non-circular tunnel, and due to the stress release achieved by applying support reaction to nodes, the method is also suitable for the tunnel with complicated stress condition. Taking the Dianzhong diversion project as an example,the numerical solution method of convergence-confinement curve was compared with the calculation results of the convergence-confinement analytical method, and the validity of the numerical solution method of convergence-confinement curve was verified. Despite some error in the result of the numerical solution method of convergence-confinement curve, the overall relative error is less than 10%. The application of the numerical solution method for convergence-confinement characteristic curve is more extensive,which can provide reference for the optimization design of primary support and safety evaluation of tunnel engineering, and the numerical solution method has a certain value of engineering application.
Key words: convergence-confinement method;tunnel;stress release method;ground reaction curve;unbalanced force;stress distribution
近年來,大型引水工程在我国各缺水地区大量建设,发展迅速,如南水北调工程、引滦入津工程、引黄入晋工程、引大入秦工程、引黄济青工程、牛栏江-滇池补水工程和滇中引水工程等.引水工程线路长,沿线地质条件复杂多变,其中,深埋引水/输水隧洞常常是这类工程的关键控制性工程,其在安全施工和健康运行的保障中所面临的围岩稳定性控制难题日益突出,如何合理评价围岩与支护结构相互作用关系以及进行隧洞支护优化设计是工程界一直关心的问题[1].收敛-约束法是工程中评价围岩与支护结构相互作用关系以及进行隧洞支护优化设计的常用方法之一,其思想由Fenner提出.目前已成为国际通用的隧洞支护设计方法.Oreste等[2]提出了一种用收敛-约束法进行圆形断面隧洞锚杆支护设计的新方法.Torres等[3]基于Hoek-Brown强度准则并利用收敛-约束法进行隧道支护设计.Cui等[4]利用虚拟支护力并结合收敛-约束法进行圆形隧洞支护设计.张常光等[5-7]探讨了收敛-约束法中的空间效应方法以及围岩塑性区变形特性对隧道收敛约束法的影响规律.苏永华等[8]基于收敛-约束法原理建立了地下结构稳定性定量评价方法.Vlachopoulos等[9]利用改进的围岩纵向特性曲线进行隧道收敛约束法分析.以上都是对静水应力作用下圆形隧洞所进行的收敛-约束法研究,而实际工程中隧洞的断面形式多样,圆形断面只是一种较为常见的断面形式,且实际地应力分布复杂多变,对于非圆形断面或非静水应力状态,收敛-约束解析法并不适用.因此,如何进行复杂断面隧洞的支护评价更加具有工程实际意义.针对收敛-约束法在非圆形隧洞中的应用,已有国内外专家学者进行探索,对于非圆形隧洞主要通过数值方法进行解决,目前常用的数值方法有两种.其中一种是利用数值方法得出非圆形隧洞断面上不同点的围岩特征曲线,然后利用收敛-约束法对隧洞不同位置进行单独分析.Nicieza等[10]在圆形断面径向位移的基础上增加断面形状函数,并利用有限差分法对断面形状函数进行拟合.孙闯等[11]、扈世民[12]和陈峰宾等[13]利用收敛-约束法分析隧洞断面不同位置的围岩稳定性和支护安全性.这些都只是对围岩一些特征点进行单独分析,并且采用同一支护特征曲线,并未考虑围岩和支护结构各点之间的相互作用,由于只分析了局部特征点,无法对整体应力、变形以及稳定性进行分析评价.另外一种是利用等效方法,将非圆形断面等效成圆形断面,然后利用数值方法分析等效后的圆形隧洞.苏永华等[14-15]和张盼凤等[16]提出了隧道非规则断面等价圆算法,利用收敛-约束法构建非圆形隧洞近似围岩特征曲线,并分析研究不同等价方法的适用性.这些都是将非圆形隧洞等效成圆形隧洞进行分析,而未考虑非圆形断面形式对围岩和支护结构变形以及应力状态的影响.为此,考虑到非圆形断面上各点围岩和支护结构的变形和应力状态不同,在隧洞开挖边界上每个节点分别施加不同的虚拟节点支撑反力,并利用应力释放法进行逐级应力释放,从而建立隧洞断面面积损失比或隧洞边界法向位移与应力释放率的关系曲线,即围岩特征曲线.通过数值方法求解非圆形隧洞未支护和已支护情况下的围岩特征曲线,进而由两种情况下围岩特征曲线得出支护结构承担的荷载以及变形,从支护结构施作到平衡整个过程中均考虑了围岩与支护结构的相互作用,这种方法在收敛-约束解析法的基础上结合应力释放法,并通过数值方法实现非圆形隧洞收敛-约束特征曲线的求解,以下称为收敛-约束特征曲线数值求解方法.
1 收敛-约束法
1.1 收敛-约束法基本原理
隧洞开挖和支护示意图如图1所示.隧洞为圆形断面,初始应力为静水应力场σ0 .在t0时刻,A-A′断面离掌子面的距离为L,此时施作初期支护,隧洞径向变形为u0r,支护结构不受力.在t时刻,A-A′断面离掌子面的距离为Lt,随着A-A′断面远离掌子面,掌子面对A-A′断面的约束作用不断减小,隧洞的径向变形增加,支护结构发生弹性变形并产生支护应力pts.在tD时刻,掌子面离A-A′断面距离较远,掌子面对A-A′断面无约束作用,此时的径向变形为uDr,支护应力为pDs.
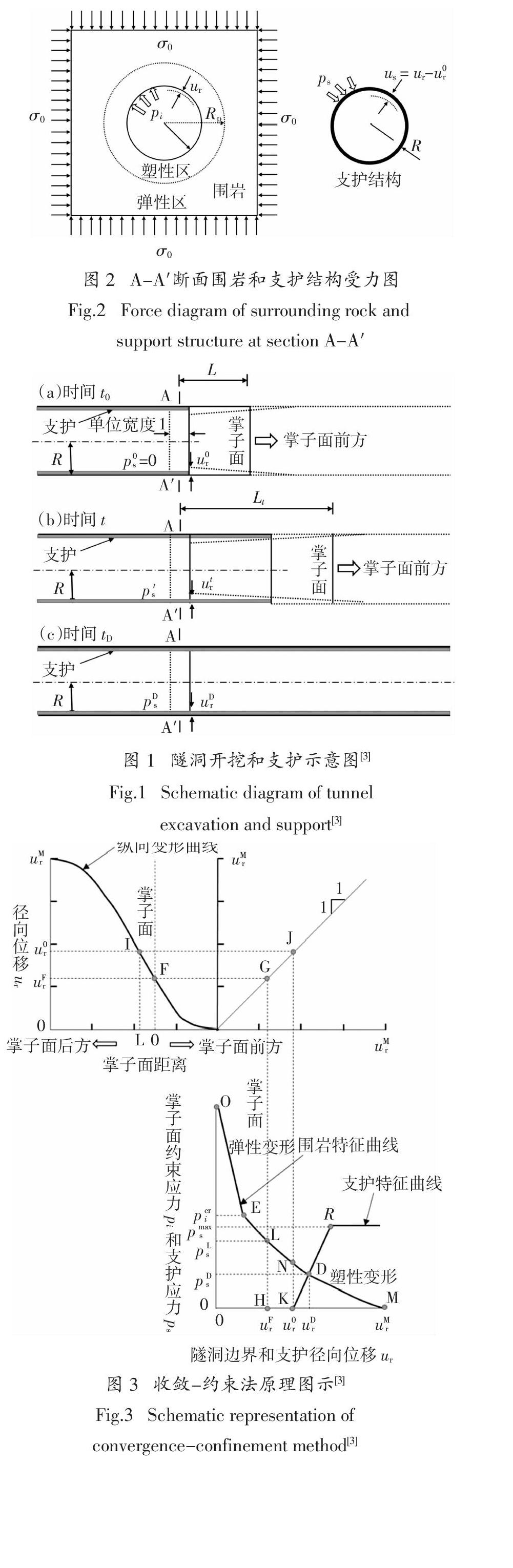
A-A′断面围岩和支护结构受力如图2所示,围岩水平和垂直应力为σ0 .隧洞开挖后,由于掌子面的约束作用,产生约束力pi,此时隧洞径向位移为ur .随着掌子面远离A-A′断面,约束力pi不断减小,当约束力减小到临界值pcri时,围岩进入塑性区,随着pi继续减小,围岩出现半径为Rp的塑性区,支护结构施作时,围岩径向位移为u0r,随着掌子面远离A-A′断面,支护结构产生的径向变形为us,同时产生支护应力为ps.
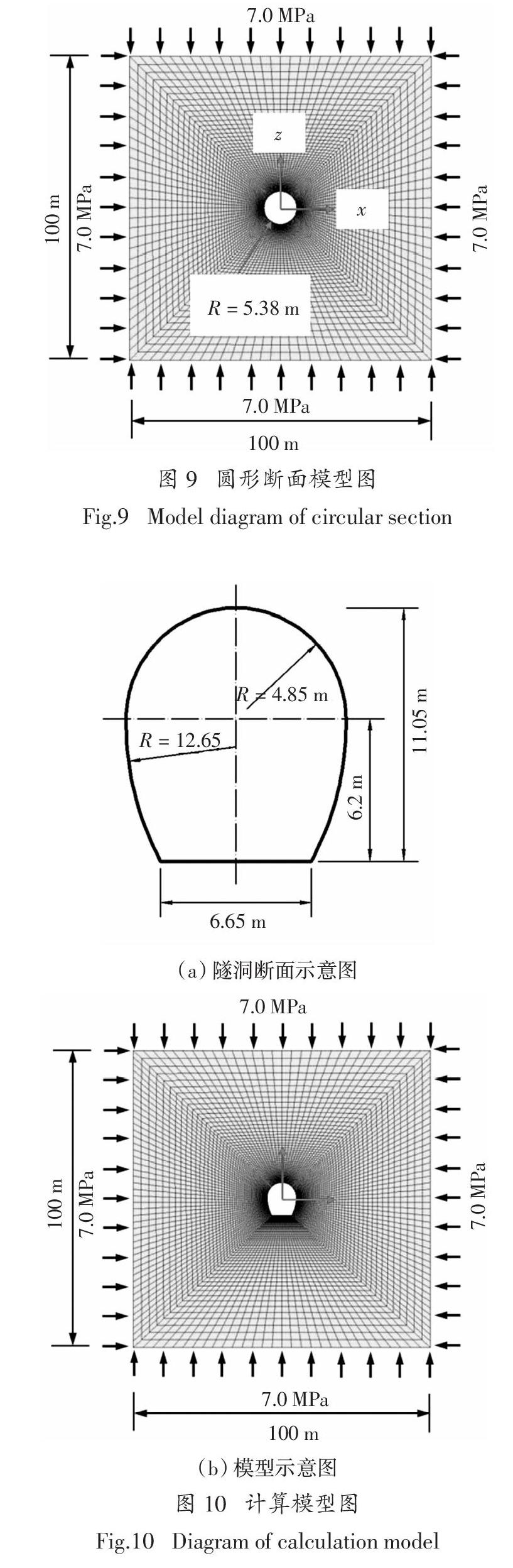
收敛-约束法基本原理如图3所示,图中3条特征曲线分别为隧洞纵向变形曲线(LDP)、围岩特征曲线(GRC)和支护特征曲线(SCC).图3左上图中纵向变形曲线(LDP)表示未支护隧洞洞壁围岩径向位移沿洞轴线的变化,坐标轴横坐标代表断面离掌子面的距离,坐标轴纵坐标代表相应断面处洞壁径向位移ur.图3右下图中围岩特征曲线(GRC)表示掌子面對断面的约束力pi与洞壁径向位移之间的关系,可以通过圆形隧洞的平面应变弹塑性解获得.
1.2 围岩和支护特征曲线解析解
1.2.1 围岩特征曲线的理想弹塑性解对于深埋圆形隧洞,假定围岩侧压力系数为1(静水应力状态),并满足均匀、连续、各向同性假定,可按无限大孔洞的求解,则其弹性收敛曲线方程为:
采用Morh-Coulomb准则,围岩弹塑性特征曲线方程为:
式中:Rp为塑性区半径,可以由式(3)计算.
以上是修正的Fenner公式,式中:ur为洞壁径向位移;R为洞室半径;σ0为围岩初始地应力;pi为约束力;E为围岩的弹性模量;c为围岩的黏聚力;v为围岩的泊松比;φ为围岩的内摩擦角.
1.2.2 支护特征曲线的确定
假定支护结构的应力-应变关系符合理想弹塑性模型,则支护特征曲线可由式(4)得到.
式中:K为支护结构刚度,其值为支护特征曲线的斜率;us为支护结构的径向位移.
对于由几种支护形式构成的组合式支护:
当组合式支护中的几种支护形式同时设置(uin,j = uin,k)时,
当组合式支护中各支护形式分别在不同的时间设置(uin,j ≠ uin,k,j ≠ k)时,
式中:Ktot为组合式支护体系的刚度;Kj为组合式支护中各单一支护的有效刚度;uin,j为组合式支护中单一支护设置时已发生的洞壁位移;u为组合支护结构的变形;Kj为组合式支护中各单一支护的刚度;uel,j为组合式支护中各单一支护达到弹性极限时的位移;Pmax,tot为组合式支护结构最大承载力;Pmax,j为组合式支护中各单一支护最大承载力;umax,tot为组合式支护结构最大允许变形值;umax,j为组合式支护中各单一支护最大允许位移值.虽然收敛约束原理能较好地解释围岩与支护结构之间的相互作用,但收敛-约束特征曲线的解析方法在未平衡时围岩和支护之间是相互独立的,且该方法存在以下局限性:1)隧洞断面为圆形;2)地层为均匀、连续、各向同性介质,初始应力场为静水压力状态;3)隧洞洞壁各点的径向位移均相同;4)难以考虑围岩自重作用的影响.对于收敛-约束法分析时存在的局限性,通过数值方法能有效地加以解决,国内外专家学者利用数值方法对上述局限性进行了一定的研究,本文在这些研究的基础上,利用数值方法并结合应力释放法原理分析隧洞围岩与支护结构的相互作用,并在整个过程中隧洞围岩和支护结构是相互接触的,两者之间相互作用和协调变形.根据收敛-约束法原理,对常用的两种数值方法进行适当的改进,提出了收敛-约束特征曲线数值求解方法.
2 收敛-约束特征曲线数值求解方法
2.1 应力释放法原理及其实现
隧洞开挖效应的数值实现方法通过两种方式实现,分别为:应力释放法和位移释放法.随着隧洞开挖以及掌子面推进,围岩应力场将发生重分布.隧洞开挖引起的应力释放主要是由于开挖的时间和空间效应.当掌子面距离某断面一定距离时,该断面应力开始发生重分布,此时未开挖围岩在该断面拟开挖边界上产生的约束应力为σd,大小等于初始应力σ0 .随着掌子面不断推进 σd不断减小,当掌子面通过该断面且有一定距离后,σd减小到σ0.则应力释放率为初始应力和拟开挖围岩对该断面开挖边界上的约束应力之差与初始应力的比值,即
隧洞开挖时应力释放宏观表现为围岩的位移释放,两者之间有十分紧密的联系,在掌子面前方一定距离处断面拟开挖边界开始发生变形,掌子面通过该断面一定距离后,洞周位移收敛,无支护开挖时洞壁所能达到的最大径向位移值为umax,隧洞开挖时某一时刻断面洞壁的径向位移值为u0,则位移释放率为某一时刻洞壁的径向位移与最终收敛位移值的比值[17],即
在模拟隧洞开挖效应时,很难直接控制隧洞洞周的位移以实现位移释放的目的,分析洞壁变形时,需要在洞壁施加虚拟的支撑反力pi,并通过逐级释放支撑反力来控制洞壁位移值,也即通过控制应力释放率间接控制位移释放率,数值分析中通过控制应力释放率模拟隧洞开挖效应也更易于实现.对于初始地应力为静水应力场的圆形断面隧洞,应力释放法模拟隧洞开挖效应的过程如图4所示,随着掌子面推进,在断面上施加虚拟支撑反力pi,pi值与应力释放率λ相关,随着掌子面推进,应力释放率 由0逐步增加到1.
有限差分原理中,应力分量为模型单元的计算参数,节点处仅有不平衡力向量,且在平衡状态下节点处的不平衡力近似为0.应力释放法的核心思想就是求得开挖前开挖边界处开挖体对围岩的支撑力(开挖掉相应单元后,支撑力随即消失),获得这一支撑力,然后控制其释放规律,达到模拟隧洞开挖的空间和时间效应.FLAC3D中开挖相应单元后,计算1步,此时得出的边界节点处的不平衡力的反力即为最大虚拟节点支撑反力.开挖前的应力场已经平衡,此时的节点速度和不平衡力均为0.开挖后,在第1步计算中应变率、应变增量及应力增量均为0,而此时的不平衡力为[18]
式中:下标i为向量分量标号;上标〈l〉为全局节点号;P 〈l〉i为施加荷载和集中力在节点〈l〉处的贡献;[[pi]]l表示拥有节点
对于初始地应力为非静水应力或断面为非圆形的隧洞,应力释放法模拟隧洞开挖效应的过程如图5所示.开挖体被开挖后,计算第1步,可以获得开挖边界上节点的不平衡力分量,开挖边界上每个节点的不平衡力合力为F ui.随着隧洞掌子面推进,在断面开挖边界节点上施加虚拟节点支撑反力F si.随着掌子面推进,应力释放率λ由0逐步增加到1,且假设在同一时刻每个节点上的应力释放率λ相同,F si随着应力释放率λ的变化而变化.
2.2 收敛-约束特征曲线数值求解方法实现
收敛-约束解析法分析时围岩和支护结构之间相互独立,仅仅通过围岩和支护特征曲线的交点确定平衡时两者之间的相互关系,并且只适合于静水应力状态的圆形隧洞,不考虑重力作用,对于应力状态和断面形状复杂的隧洞并不适用.而收敛-约束特征曲线数值求解方法在整个过程中均考虑了围岩和支护结构的相互作用关系,支护特征曲线反映了从支护施作到平衡的整个过程中支护结构的应力状态和变形,而收敛-约束解析法未考虑围岩和支护结构在整个过程中的相互作用,并且收敛-约束特征曲线数值求解方法适用于应力状态和断面形式复杂的隧洞.
图6所示为静水应力状态马蹄形断面法向位移分布图(法向位移放大10倍),可以看出,开挖边界上各点的位移并不相同.
如图6所示隧洞边界上各点法向位移不相同,为统一描述开挖面的变形情况,引入隧洞断面面积损失比的概念.隧洞开挖后围岩会向洞室内变形,造成隧洞断面面积减小,隧洞断面的面积损失比s为隧洞开挖边界线与变形后边界线围成的面积SL与隧洞断面面积SA的比值,即
收敛-约束特征曲线数值求解方法原理如图7所示,图中λ为应力释放率.由于支护结构每个部位的变形不相同,承担的荷载为非均布荷载,支护结构承担的荷载采用荷载比α表示,其值表示支护承担的荷载占开挖释放总荷载的比值.图7中纵坐标为应力释放率λ和支护承担荷载比α,而横坐标可以根据实际情况选择断面面积损失比或隧洞边界法向位移.围岩特征曲线表示围岩应力释放率与断面面积损失比或隧洞边界法向位移之间的关系曲线,曲线OSE为未支护围岩特征曲线,在整个模拟过程中,假设未施加支护结构,隧洞边界只受到虚拟节点支撑反力作用,曲线OSE′为已支护围岩特征曲线,当应力释放率在0 ~ λ0区间时,隧洞边界只受到虚拟节点支撑反力作用,此阶段的曲线与未支护围岩特征曲线重合,而应力释放率在λ0 ~ 1区间时,隧洞受到虚拟节点支撑反力和支护结构的支撑反力作用,点S为支护作用的点,根据LDP曲线确定初期支护施作时的应力释放率为 0,两条曲线的OS段重合;由于支护结构受力条件复杂,支护特征曲线不能按式(4)直接求解,收敛-约束特征曲线数值求解方法是利用已支护和未支护围岩特征曲线求解,支护特征曲线的起点S′是由初期支护架设时间决定的,由E′作横坐标垂线与曲线OSE交于点B,该点为支护特征曲线的终点,此时点B对应的纵坐标值λb为平衡时围岩分担的荷载,αb为平衡时支护结构承担的荷载比.支护荷载计算示意图如图8所示,未支护情况,围岩应力释放率为λ1,此时对应图7中的点R1,已支护情况,围岩应力释放率为λ2,此时对应图7中的点R2.
如图8所示,未支护和已支护情况下,当隧洞边界法向位移或断面面积损失比相等时,围岩边界节点上总的反力相等.如图7所示,已支护围岩特征曲线在点R2时,围岩应力释放率为λ2,而未支护围岩特征在点R1时,围岩应力释放率为λ1,已支护围岩比未支护围岩的应力释放率要高(λ2 - λ1).如图8所示,未支护情况下,隧洞开挖边界只受到虚拟节点支撑反力作用,将虚拟节点支撑反力拆分为F 2i和F 12i两部分.已支护情况下,隧洞边界上受到支护结构支撑作用,将支护结构独立出来,此时隧洞开挖边界受到的反力分为虚拟节点支撑反力F 2i和支护反力F SLi两部分.当两种情况下隧洞开挖边界每个节点上的位移相等时,认为开挖边界上每个节点受到的总反力相等,即F 2i + F 12i = F 2i + F SLi,从而得出F SLi = F 12i,进而得出支护结构承担的荷载比αR = λ2 -λ1.而这两种情况下隧洞边界上每个节点位移并非完全相等,此时很难保证每个节点上F SLi = F 12i,利用统一的荷载比αR表示每个节点的荷载比会产生一定误差,具体分析过程如下.
式中:[[Ai]]l表示拥有节点i的所有开挖边界的面积对节点i的贡献之和; 为节点i在开挖面上所占的有效面積;R为节点i处的等效半径;uunsi 为未支护时,节点i的位移;usi为已支护时,节点i的位移;F ui 为节点i的最大不平衡节点力;F si 为节点i的虚拟支撑反力(施加在隧洞洞周边界点上);λi1为未支护时,节点i的应力释放率;F SLi 为支护结构对节点i的支撑反力;λi2为已支护时,节点i的应力释放率;αi为节点i处支护结构承担的荷载比;ξ表示与本构模型相关的参数,对于弹性变形阶段或弹性本构模型其值为1.
当其中某一个节点j(j = 1,i)未支护和已支护时的位移相等,即uunsj = usj 时,对于同一个节点ξ相同,由式(16)~(19)可知αj = λj2 - λj1,由于假设同一时刻不同节点的应力释放率相等,也即节点j上的支护结构承担的荷载比α = λ2 - λ1.若其他节点k(k =1,i且k ≠ j)上的支护结构承担的荷载比也为α= λ2 - λ1,则此时节点k未支护和已支护时的位移相等,即uunsk = usk .而实际上节点k(k = 1,i且k ≠ j)上的支护结构承担的荷载比αk与节点j上的支护结构承担的荷载比α不相等,存在一定的误差;当节点k上支护结构承担的荷载比αk取α时,节点k的位移为uk = uunsk ,而当节点k上支护结构承担的荷载比αk为真实值αt时,节点k的位移为uk = usk ,则可利用节点位移相对误差表示支护结构承当的荷载比相对误差,即
式(20)是利用某一节点位移相对误差表示支护结构承担的荷载比α的相对误差,而每个节点的位移相对误差值不相等,为等效表示所有节点支护荷载比α的相对误差,也可利用隧洞边界变形后断面面积损失比相对误差表示支护结构承担的荷载比α的相对误差,即
3 工程实例
为验证收敛-约束特征曲线数值求解方法的有效性,本文以滇中引水工程为背景,利用收敛-约束特征曲线数值求解方法和收敛-约束解析法进行圆形隧洞(与马蹄形断面面积相等,半径为5.38 m)支护研究,并对数值解与解析解进行对比.通过与解析解对比验证收敛-约束特征曲线数值求解方法的有效性,利用收敛-约束特征曲线数值求解方法分析马蹄形隧洞,并与常用的两种数值方法进行对比研究,最后分析收敛-约束特征曲线数值求解方法的计算误差.
3.1 工程概况以及模拟过程
滇中引水工程中万家-罗茨段隧洞埋深一般为200 ~ 400 m,最大埋深640 m.隧洞穿越地层以“滇中红层”的泥岩、泥质粉砂岩、粉砂岩、泥灰岩及砂岩等为主,在线路末段部分出露有下元古界昆阳群泥质板岩、粉砂质板岩等变质岩和震旦系白云岩、白云质灰岩等碳酸盐岩.引水隧洞断面为马蹄形,如图10(a)所示,验证收敛-约束特征曲线数值求解方法有效性时采用与马蹄形隧洞断面等面积的圆形隧洞,隧洞断面模型图如图9所示.在验证收敛-约束特征曲线数值求解方法有效性基础上,利用该方法分析马蹄形隧洞,数值计算模型如图10(b)所示,并与常用的2种数值方法进行对比.常用的数值方法分析思路:方法1,在马蹄形隧洞边界上施加均布支护阻力pi,其值由7 MPa逐步减小到0,同时对隧洞开挖边界上的6个点进行位移监测,从而得出监测点1~6的位移随支护阻力变化的曲线,即围岩特征曲线.方法2,利用面积等效法,将马蹄形隧洞等效为半径为5.38 m的圆形隧洞,通过上述方法得出围岩特征曲线.这两种方法的支护特征曲线均按式(4)得到,最后利用数值法得到的围岩特征曲线和解析法得到的支护特征曲线进行非圆形隧洞支护设计.收敛-约束特征曲线数值求解方法分析思路:通过开挖瞬间获得隧洞开挖边界节点上的最大不平衡力
逐步增加应力释放率λ的值获得隧洞边界位移与不同应力释放率之间的关系曲线,即围岩特征曲线.收敛-约束特征曲线数值求解方法得到两种围岩特征曲线,分别为:未支护围岩特征曲线和已支护围岩特征曲线.在隧洞整个开挖过程中,假设不施加任何支护结构,隧洞开挖边界只受到虚拟节点支撑反力作用,通过上述方法获得隧洞边界位移与不同应力释放率之间的关系曲线,即未支护围岩特征曲线;在隧洞开挖过程中施加支护结构,当应力释放率为λ0时,支护结构发挥作用,此时隧洞开挖边界受到虚拟节点支撑反力和支护反力作用,通过相同的方法获得已支护围岩特征曲线,根据已支护围岩特征曲线与未支护围岩特征曲线之间的差得到支护特征曲线,如图7所示.为保证结果的可比性,初始地应力均为静水应力状态,值为7.0 MPa.初期支护模拟时,不考虑钢筋网的影响,喷射混凝土作为实体单元考虑,不单独考虑钢支撑,而是把它的影响结合到喷射混凝土中,将钢支撑和喷射混凝土等效成一个整体,并采用实体单元模拟,系统锚杆采用FLAC3D中的锚索结构单元.挂网喷混凝土、锚杆以及钢支撑等工序在施工过程中存在一定的先后顺序,在实际中发挥作用的时间先后也不同,本文未研究不同支护工序发挥作用的时机对隧洞支护设计的影响,在进行分析时,假设支护体系中各工序同时发挥作用.围岩采用摩尔-库仑本构模型进行分析,喷射混凝土以及钢支撑与喷射混凝土的等效体采用弹性本构模型进行分析.
3.2 围岩与支护参数
不同围岩级别对应的岩体力学参数建议取值如表1所示,不同围岩级别对应的初期支护类型如表2所示,将钢支撑和喷射混凝土等效成一个整体,并采用等效参数进行模拟,支护结构参数如表3所示.
3.3 收敛-约束特征曲线数值求解方法验证
收敛-约束特征曲线数值求解方法与解析法对比结果如图11所示,未支护围岩特征曲线(数值法)与围岩特征曲线(解析法)几乎重合,在弹性阶段,这两条曲线完全重合.随着支护阻力不断减小和应力释放率不断增加,两条曲线逐渐分开,数值法与解析法得出的支护特征曲线几乎重合或平行.
對收敛-约束特征曲线数值求解方法与解析法计算结果进行对比分析,并分析数值结果与解析结果的相对误差,分别如表4和表5所示.Ⅲ级围岩的围岩和支护结构最大位移相对误差最小,Ⅴ级围岩的围岩最大位移相对误差最大,为6.21%,Ⅳ级围岩的支护结构最大位移相对误差最大,为9.87%.Ⅲ~Ⅴ级围岩的支护结构承担荷载相对误差均较小,其中Ⅲ级围岩最大,为6.14%,Ⅴ级围岩最小,为1.16%.收敛-约束数值方法与解析法结果的相对误差较小,验证了收敛-约束数值方法的有效性.
3.4 计算结果对比分析
利用常用的数值方法和收敛-约束特征曲线数值求解方法进行马蹄形隧洞(图10(a))支护设计,对比分析结果如图12~图14所示,图中标明了马蹄形隧洞开挖边界上的监测点位置,断面等效法和收敛-约束数值法均取拱顶为研究对象.收敛-约束特征曲线数值求解方法中未支护围岩特征曲线、已支护围岩特征曲线和支护特征曲线均通过数值方法获得,而常用的数值方法中,围岩特征曲线通过数值方法获得,支护特征曲线通过解析法获得.收敛-约束特征曲线数值求解方法是通过在隧洞开挖边界节点上施加虚拟节点支撑反力,常用的数值方法是通过在隧洞开挖边界上施加均布荷载,在围岩应力状态复杂情况下,常用的数值方法很难模拟,而收敛-约束特征曲线数值求解方法是在边界节点上施加虚拟节点支撑反力,每个节点上力的大小和方向相互独立,对于复杂的应力状态也适用.
Ⅲ级围岩对比结果如图12所示,根据收敛-约束特征曲线数值求解方法结果,支护结构位移为4.14 mm,支护承担的荷载比为12.06%,等效荷载值约为7 MPa×12.06%=0.84 MPa;根据断面等效法结果,支护结构位移为4.88 mm,等效支护荷载为0.68 MPa;而马蹄形隧洞6个监测点的围岩特征曲线均不相同,根据不同监测点得到的支护结构位移和变形不一样,其中支护结构最大位移为5.85 mm,最大支护荷载为0.81 MPa,支护结构最小位移为3.62 mm,最小支护荷载为0.50 MPa.
Ⅳ级围岩对比结果如图13所示,根据收敛-约束特征曲线数值求解方法结果,支护结构位移为5.61 mm,支护承担的荷载比为19.82%,等效荷载值约为7 MPa × 19.82% = 1.39 MPa;根据断面等效法结果,支护结构位移为7.44 mm,等效支护荷载为1.35 MPa;而马蹄形隧洞6个监测点的围岩特征曲线均不相同,根据不同监测点得到的支护结构位移和变形不一样,其中支护结构最大位移为8.37 mm,最大支护荷载为1.48 MPa,最大荷载已经接近支护结构最大能承担的荷载值,支护结构最小位移为5.74 mm,最小支护荷载为1.04 MPa.
Ⅴ级围岩对比结果如图14所示,根据收敛-约束特征曲线数值求解方法结果,支护结构位移为0.90 mm,支护承担的荷载比为7.41%,等效荷载值约为7 MPa × 7.41% = 0.52 MPa;根据断面等效法结果,支护结构位移为2.17 mm,等效支护荷载为0.59 MPa;而马蹄形隧洞6个监测点的围岩特征曲线均不相同,根据不同监测点得到的支护结构位移和变形不一样,其中支护结构最大位移为3.37 mm,最大支护荷载为0.75 MPa,最大荷载已经接近支护结构最大能承担的荷载值,支护结构最小位移为2.37 mm,最小支护荷载为0.47 MPa.
常用数值方法中,直接采用马蹄形隧洞进行模拟,由于隧洞开挖边界上每个点的位移和支护结构承担的荷载不同,很难通过某一点的支护状态反映马蹄形隧洞支护情况,而断面等效法,由于隧洞断面形态发生改变,支护结构的形状和受到的应力状态与马蹄形隧洞不一致.常用数值方法中,隧洞开挖边界上施加均布荷载,当围岩应力状态较复杂时,施加均布荷载不合适,模拟过程中,围岩特征曲线和支护特征曲线是分开得到的,而支护结构施作后,围岩与支护结构相互作用,最后处于平衡状态,该方法只能考虑处于平衡状态时,支护结构的变形和承担的荷载.而收敛-约束特征曲线数值求解方法模拟过程中,虚拟支撑反力是施加在隧洞开挖边界节点上,每个节点上支撑反力的大小和方向可以不同,当围岩应力状态复杂时,可以通过在边界节点上施加不同的虚拟支撑反力,该方法在模拟时,支护结构施作后,围岩和支护结构接触,两者相互作用,协调变形,支护结构各点之间也会相互影响,通过该方法可以获得支护结构施作到平衡整个过程中围岩和支护结构的受力状态和变形.
3.5 误差分析
在实际工程中,隧洞开挖后一定要采取适当的支护措施,而本文中未支护情况是假设隧洞开挖过程中未施加支护作用.未支护情况下,隧洞边界只受到虚拟节点支撑反力作用,支护情况下,当支护结构发挥作用后,隧洞边界受到虚拟节点支撑反力和支护反力作用.当这两种情况下隧洞变形后边界完全重合,也即隧洞边界受到的总的反力相等,从而根据两种情况下虚拟节点支撑反力的差值得到支护反力.而收敛-约束特征曲线数值求解方法进行非圆形隧洞支护计算时,由于假设支护结构与围岩间的每个节点承担的荷载比相同,结果会产生一定的误差,相对误差可根据公式(21)和(22)计算.根据3.4节内容可知,Ⅲ级围岩收敛-约束特征曲线数值求解方法与常用的数值方法得到的支护荷载相差较大,本文以Ⅲ级围岩为例分析收敛-约束特征曲线数值求解方法计算误差.拱顶位移相等时,Ⅲ级围岩已支护和未支护情况下隧洞变形后边界线如图15所示(位移值放大100倍),由图可知两种情况下边界变形曲线基本重合,整体相差较小,拱底处位移相差较大.根据公式(21)和(22)计算收敛-约束特征曲线数值求解方法的相对误差如表6所示.随着围岩应力不断释放,支护结构承担的荷载比由0逐步增加到12.06%,断面面积损失和最大位移相对误差也随之增加,最大位移相对误差为11.03%,则其他边界点的位移相对误差均小于11.03%,面积相对误差仅为5.87%,其可代表收敛-约束特征曲线数值求解方法结果的整体相对误差水平.
4 结 论
本文提出了考虑非圆形隧洞的收斂-约束特征曲线数值求解方法,并以滇中引水工程万家-罗茨段隧洞为例,通过与收敛-约束解析法对比验证了该方法的有效性,并与常用的数值方法进行对比分析,最后对收敛-约束特征曲线数值求解方法进行误差分析.主要结论如下:
1)利用有限差分方法计算开挖瞬时隧洞边界节点上的不平衡力,然后通过对开挖边界节点施加反向不平衡力并逐步减小节点反力的大小模拟非静水压力状态的非圆形隧洞开挖时的应力释放过程.该方法能更好地模拟围岩和支护结构的相互作用关系以及不同点间的相互约束作用.
2)基于收敛约束法原理,并在收敛约束解析法基础上提出了收敛-约束特征曲线数值求解方法.该方法适合非圆形隧洞,对于初始应力为非静水压力状态同样适合,而收敛-约束解析法仅适合静水压力状态的圆形隧洞,收敛-约束特征曲线数值求解方法适用范围更广.
3)以滇中引水工程中万家-罗茨段隧洞为例,通过与收敛-约束解析法进行对比,验证了收斂-约束特征曲线数值求解方法的有效性,并与常用的数值方法进行对比,在进行非圆形隧洞支护设计时,收敛-约束特征曲线数值求解方法更合适.
4)由于收敛-约束特征曲线数值求解方法假设支护结构与围岩间的每个节点承担的荷载比相同,结果会产生一定的误差,以Ⅲ级围岩为例分析收敛-约束特征曲线数值求解方法的计算相对误差.随着围岩应力不断释放,支护结构承担的荷载比随之增加,面积损失和位移相对误差也变大,平衡后最大位移相对误差为11.03%,而面积损失相对误差仅为5.87%.
参考文献
[1] 周辉,高阳,张传庆,等. 考虑围岩衬砌相互作用的钢筋混凝土衬砌数值模拟[J]. 水利学报,2016,47(6):763-771.
ZHOU H,GAO Y,ZHANG C Q,et al. Numerical simulation of reinforced concrete lining considering the interaction with the surrounding rock[J]. Journal of Hydraulic Engineering,2016,47(6):763-771.(In Chinese)
[2] ORESTE P P,PEILA D. Radial passive rockbolting in tunnelling design with a new convergence-confinement Model[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1996,33(5):443-454.
[3] TORRES C C,FAIRHURST C. Application of the convergence-confinement method of tunnel design to rock masses that satisfy the hoek-brown failure criterion[J]. Tunnelling and Underground Space Technology,2000,15(2):187-213.
[4] CUI L,ZHENG J J,ZHANG R J,et al. A numerical procedure for the fictitious support pressure in the application of the convergence-confinement method for circular tunnel design[J]. International Journal of Rock Mechanics and Mining Sciences,2015,78:336-349.
[5] 张常光,曾开华. 收敛约束法中隧道开挖面空间效应方法比较[J]. 岩土力学,2016,37(5):1417-1424.
ZHANG C G,ZENG K H. Comparisons of spatial-effect approaches for tunnel excavation using convergence-confinement method[J]. Rock and Soil Mechanics,2016,37(5):1417-1424.(In Chinese)
[6] 张常光,赵均海,范文. 围岩塑性区变形特性对隧道收敛约束的影响[J]. 中国公路学报,2016,29(3):106-115.
ZHANG C G,ZHAO J H,FAN W. Influence of deformation characteristics of surrounding rock inplastic zone on tunnel convergence-confinement [J]. China Journal of Highway and Transport,2016, 29(3):106-115.(In Chinese)
[7] 张常光,曾开华. 等值地应力下岩质圆形隧道位移释放系数比较及应用[J]. 岩石力学与工程学报,2015,34(3):72-84.
ZHANG C G,ZENG K H. Comparisons and applications of displacement release coefficients for a circular rock tunnel subjected to isotropic geostresses [J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(3):72-84.(In Chinese)
[8] 苏永华,付雄,肖旺.围岩收敛曲线形态对地下结构稳定系数影响分析[J].湖南大学学报(自然科学版),2015,42(7):87-92.
SU Y H,FU X,XIAO W. The analysis for stability coefficient of underground structure with the shapes of ground response curves[J]. Journal of Hunan University(Natural Sciences),2015,42(7):87—92.(In Chinese)
[9] VLACHOPOULOS N,DIEDERICHS M S. Improved longitudinal displacement profiles for convergence confinement analysis of deep tunnels[J]. Rock Mechanics and Rock Engineering,2009,42(2):131—146.
[10] NICIEZA C G,ALVAREZ-VIGILB A E,MENENDEZ-DLAZC A,et al. Influence of the depth and shape of a tunnel in the application of the convergence-confinement method[J]. Tunnelling and Underground Space Technology,2008,23(1):25—37.
[11] 孫闯,张向东,李永靖. 高应力软岩巷道围岩与支护结构相互作用分析[J]. 岩土力学,2013,34(9):2601—2607.
SUN C,ZHANG X D,LI Y J. Analysis of interaction between surrounding rock and support structure in high stressed soft rock roadway[J]. Rock and Soil Mechanics,2013,34(9):2601—2607. (In Chinese)
[12] 扈世民.基于收敛-约束法地铁区间隧道初期支护安全性研究[J]. 铁道学报,2015,37(10):117—121.
HU S M. Research on safety of initial support in metro regional tunnel based on convergence-confinement method[J]. Journal of the China Railway Society,2015,37(10):117—121.(In Chinese)
[13] 陈峰宾,张顶立,扈世民,等. 基于收敛约束原理的大断面黄土隧道围岩与初支稳定性分析[J].北京交通大学学报,2011,35(4):32—36.
CHEN F B,ZHANG D L,HU S M,et al. Stability analysis of surrounding rock and supports in large-span loess tunnel using the convergence-confinement method[J]. Journal of Beijing Jiaotong University,2011,35(4):32—36.(In Chinese)
[14] 苏永华,刘少峰,王凯旋,等. 基于收敛-约束原理的地下结构稳定性分析[J]. 岩土工程学报,2014,36(11):2002—2009.
SU Y H,LIU S F,WANG K X,et al. Stability analysis of underground structures based on convergence-confinement method[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(11):2002—2009.(In Chinese)
[15] 苏永华,张盼凤,肖旺. 剪胀围岩隧道开挖响应曲线的等价圆近似法[J]. 岩土工程学报,2015,37(S1):31—35.
SU Y H,ZHANG P F,XIAO W. Equivalent circular approximation method for response curve tunnel excavation of dilatant surrounding rock[J]. Chinese Journal of Geotechnical Engineering,2015,37(S1):31—35.(In Chinese)
[16] 张盼凤,苏永华,王凯旋,等. 非圆形地下洞室地层特征曲线近似构建法[J]. 水文地质工程地质,2015,42(2):58—64.
ZHANG P F,SU Y H,WANG K X,et al. An approximate building method of ground reaction curve for non-circular underground caverns[J]. Hydrogeology & Engineering Geology,2015,42(2):58—64.(In Chinese)
[17] 苏永华,孙旺,方砚兵. 基于正交试验的隧道开挖面位移释放分析[J]. 湖南大学学报(自然科学版),2017,44(11):157—164.
SUN Y H,SUN W,FANG Y B. Analysis on displacement release of tunnel face based on orthogonal tests[J]. Journal of Hunan University(Natural Sciences),2017,44(11):157—164.(In Chinese)
[18] 张传庆,冯夏庭,周辉,等. 应力释放法在隧洞开挖模拟中若干问题的研究[J]. 岩土力学,2008,29(5):31—37.
ZHANG C Q,FENG X T,ZHOU H,et al. Study of some problems about application of stress release method to tunnel excavation simulation[J]. Rock and Soil Mechanics,2008,29(5):31—37. (In Chinese)
收稿日期:2018-05-27
基金项目:国家自然科学基金资助项目(51427803,51479193,51404240),National Natural Science Foundation of China(51427803,
51479193,51404240);国家重点基础研究发展计划(973计划)项目(2014CB046902),National Program on Key Basic Research Project of China(973 Program)(2014CB046902)
作者简介:周辉(1972—),男,山东金乡人,中国科学院武汉岩土力学研究所研究员,博士
通讯联系人,E-mail:154308390@qq.com
