OPTA细化算法在跳频信号参数估计中的应用*

王欣怡,南心蒙,李柯达,王 健,范中平

(西安现代控制技术研究所, 西安 710065)

0 引言

跳频通讯[1]因具有优良的抗干扰性而被广泛应用于军事通讯传输中,该通讯模式下常采用的跳频信号,是一种载频伴随一组随机分布的伪码进行离散跳变的非平稳信号,因其信号频率值具有多变性及不稳定性而具备较强的抗检测、抗侦察能力。因此对跳频信号进行参数估计的深入研究是十分必要的。

传统的跳频信号参数估计方法为直接采用时频图像进行的估计,其中含有的噪声及信号分布存在的宽度,会对参数估计的准确性产生较大影响。因此文中提出改进方法,即首先对采集到的跳频信号进行二维时频分析,得到信号的二维时频图像,其次通过采用形态滤波、阈值分割及 OPTA细化对信号的时频图像进行降噪与细化,优化图像效果,突出有用目标信息。

1 跳频信号模型

文中研究的跳频信号模型如式(1)所示:

(1)

式中：TH为各特定载波频率值持续周期；T0为初始跳变时刻；fm是第m个载波频率值；N为载频个数；ω(t)是均值为0的高斯白噪声。

2 跳频信号SPWVD时频分析

时间和频率是信号研究中两个不可忽略的重要指标。在各类传统分析方法中,时频分析[2]由于具备将信号的时间和频率相结合进行同步分析并能够在二维空间中将其对应关系呈现出来的优势,得到了广泛的应用。

现有常见的时频分析方法包含:WVD(维格纳分布)、PWVD(伪维格纳分布)、SPWVD(平滑伪维格纳分布)[3]、STFT(短时傅里叶变换)[4]等。由于信号的能量有限,其时宽带宽积存在下限,因此采用STFT方法对信号进行分析，无法很好权衡时间分辨率与频率分辨率。采用PWVD与WVD进行分析时,虽然分辨率有所提升,但结果存在较为严重的干扰交叉项,对信号的估计不利。相比之下采用SPWVD对信号进行分析具备高时间分辨率、频率分辨率、交叉项少的优点,因此文中采用SPWVD方法进行信号的分析。

3 跳频信号时频图像处理流程

3.1 形态学滤波去噪

接收信号中的噪声会对信号的估计产生直接影响,文中选用形态学滤波[5]对信号时频图像进行必要的去噪处理。

结构元素作为形态学滤波中的关键所在，其具体分布与尺寸直接影响着去噪效果。通常小尺寸的结构元素具有较强的分辨力,但其去噪能力较弱;大尺寸的元素具有较强的去噪能力,但对于图像边沿的提取能力相对薄弱。文中将两类结构元素相结合,采用多尺度结构元素[6]对图像进行去噪处理,优化图像效果。

基于信号分布特点及噪点分布情况,首先采用大尺度结构元素对图像进行腐蚀处理以去除噪声如图1(a);之后使用小尺度结构元素见图1(b)，对时频图像进行膨胀操作,对图像边缘部分进行识别并针对腐蚀处理后导致的图像边缘连续性遭到破坏的部分进行修复,最大限度还原出信号的有效信息成分,提升信噪比。图2为经过腐蚀膨胀后的时频图像效果对比图,其中图2(a)为原始含噪时频图像,图2(b)为处理后图像,可以看出此时大量干扰噪点已被去除。

表1为图2中两幅图像对应的PSNR(峰值信噪比)数值对照表,结果显示经过滤波后的图像PSNR值提升,图像质量优于原始图像。

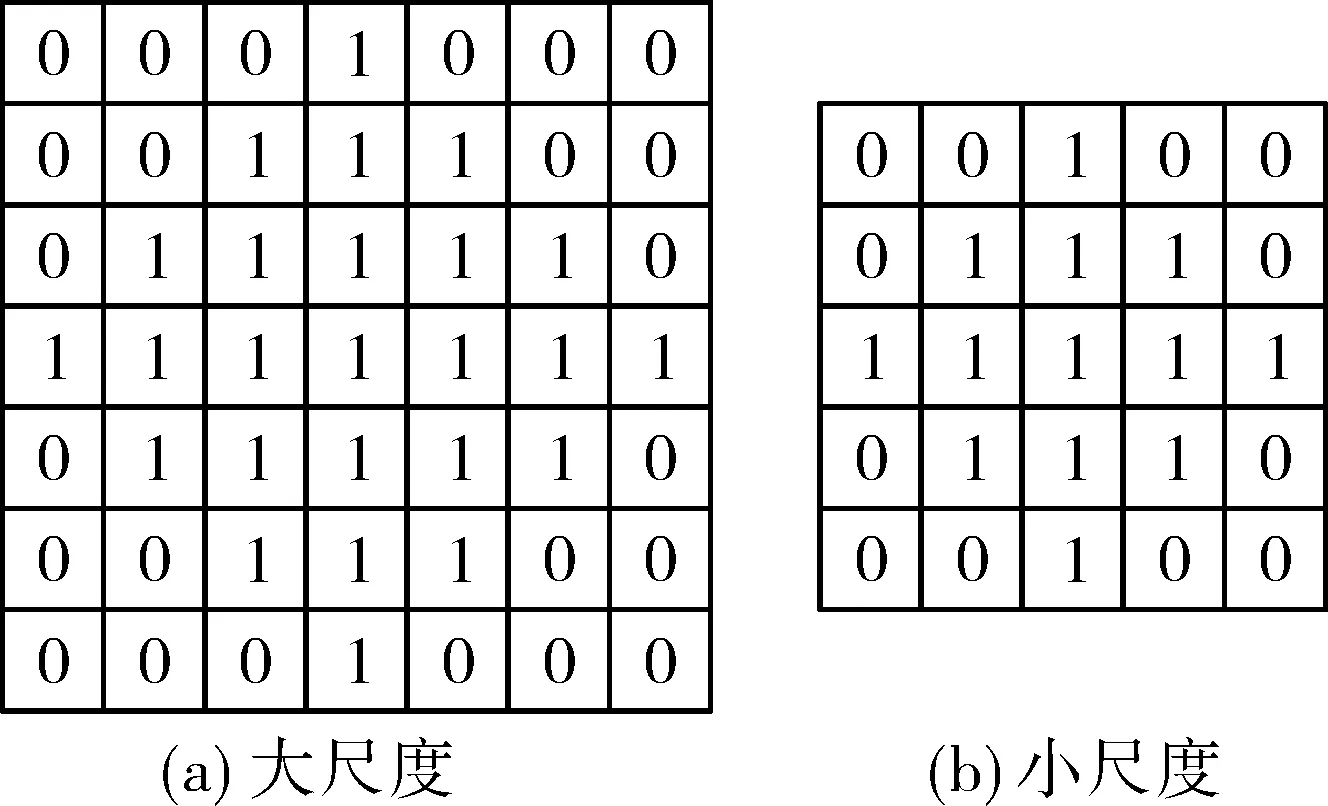
图1 结构元素

图2 示例跳频信号降噪效果图

表1 降噪效果数据对比表

3.2 阈值分割

经过去噪后的信号时频图像,为更方便的获取目标,需采用阈值分割[7]的方法对图像进行二值化。采用迭代阈值的方法,即首先求取图像中所有像素点的平均值作为初始阈值s,以此阈值将图像像素点分为目标和背景两部分,分别计算两部分像素值的均值记作s1和s2,之后以(s1+s2)/2为新阈值,对图像像素点进行再次分割,以此迭代,直至阈值不再变化为止,以最终得到的阈值为标准,对图像进行二值化。

3.3 OPTA细化算法

经过阈值分割处理后的时频分布仍存在一定宽度,若直接用来进行参数的估计会产生相应偏差,因此采用典型的迭代并行细化处理——OPTA 细化算法[8]对图像进行细化。

OPTA细化算法的关键之处在于对比模板的设计。文中在传统算法模板的基础上结合信号特点,做了一定改进,具体细化流程可以分为以下4个步骤:

1)以自上至下,从左到右的顺序依次遍历图像中各像素点,以如图3中的P点为当前像素点,选取其周围临近的10个像素点。若当前点为背景点,则跳过,否则与图4中的预处理模板进行对比,若符合模板图4(a)～图4(d)中的任意一个,则将该像素点值置0,若符合其余的4个模板,则置1。

2)将当前像素点P及周围邻近8个像素点(P1～P8)继续与图5中的消除模板进行比较,若消除模板中未找寻到与之匹配的模板,则将该点值保留,否则进入步骤3)。

3)将当前像素点及周边点与图6中的保留模板对比,若存在符合的模板,则将该点值保留,否则置0(其中1表示目标点,0表示背景点,× 代表0或1)。

4)以前三步为单独像素点处理步骤,以遍历整个图像一次为一轮迭代,反复循环执行比对,直至无像素点值可变为止,此时代表细化完成。

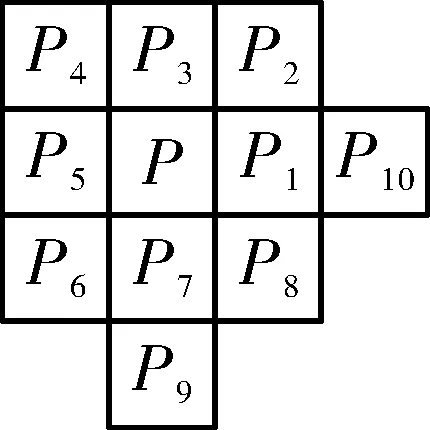
图3 结构元素

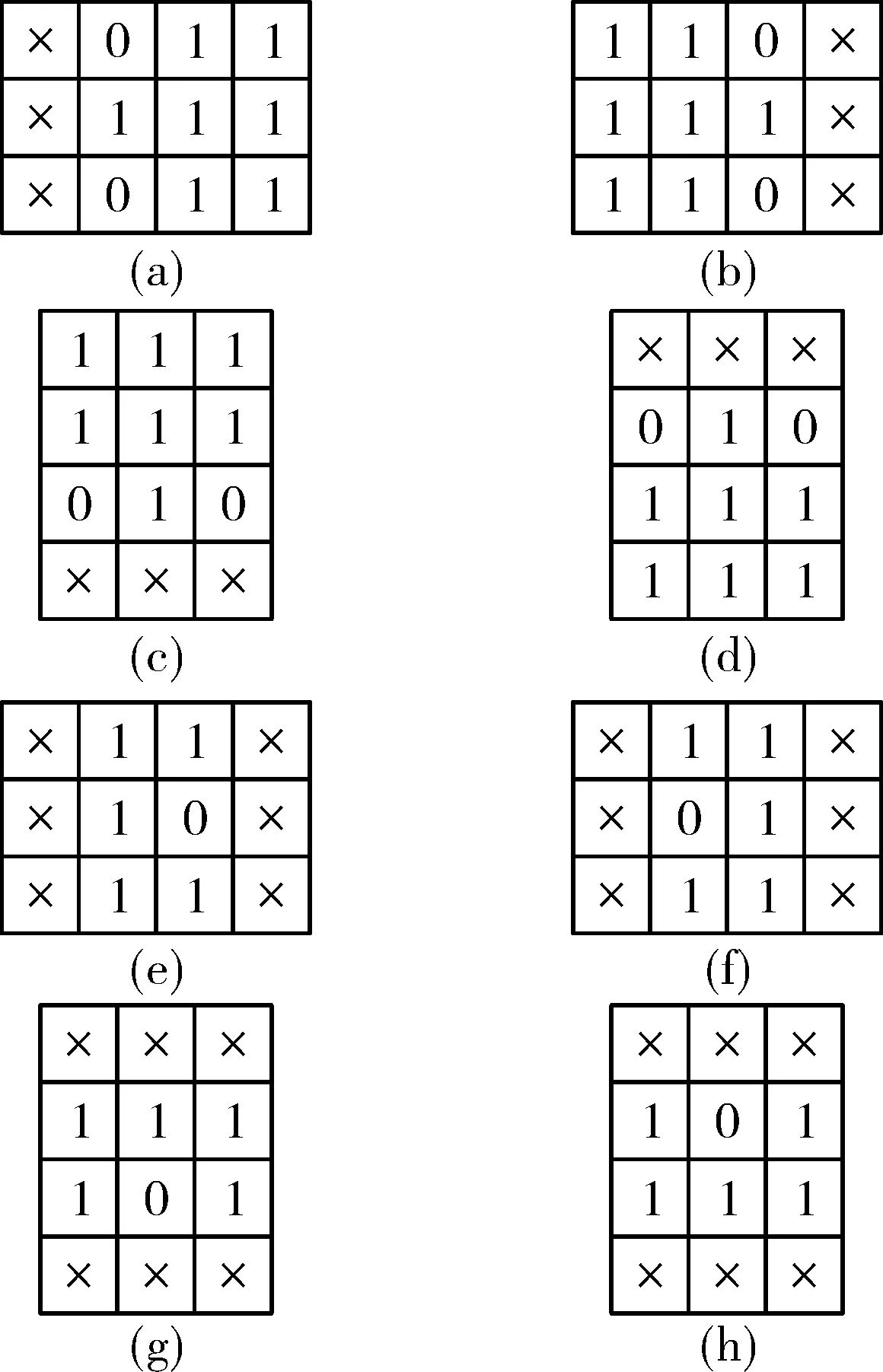
图4 预处理模板

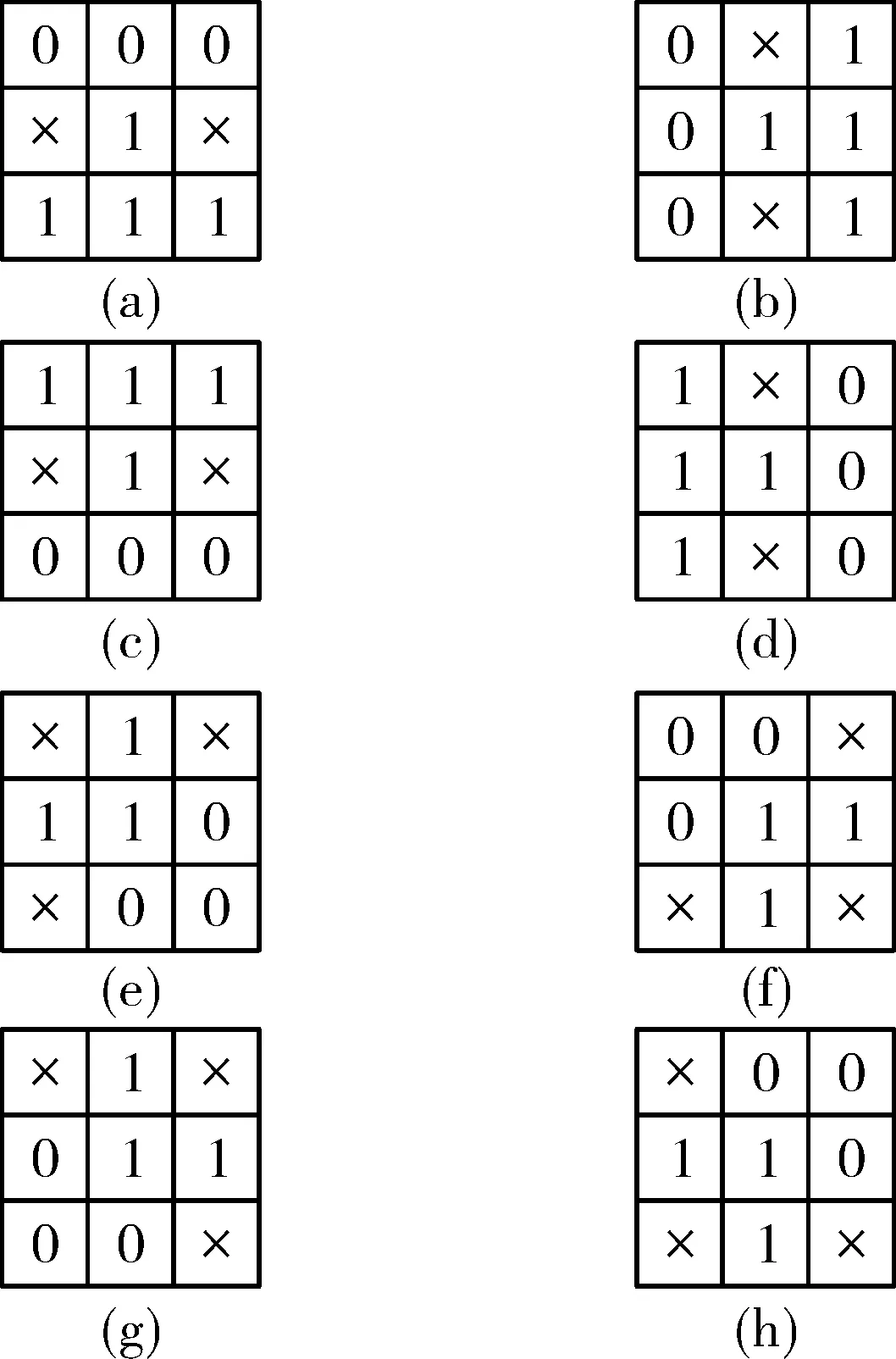
图5 消除模板

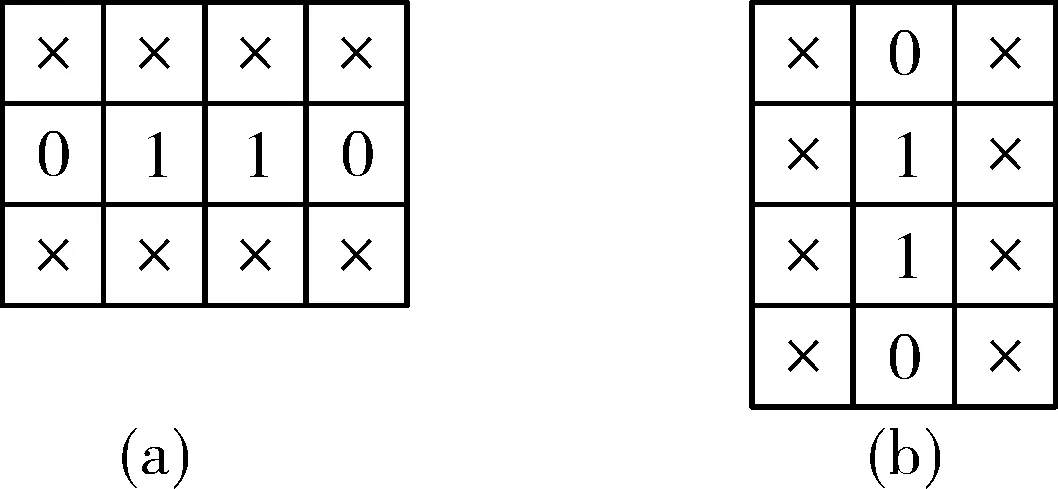
图6 保留模板

4 仿真结果及分析

选取采样频率为9 667 kHz,各跳频率分别为[400,1 000,600,1 200,1 900,1 400] ,单位为kHz,跳时为1/3 000 s,跳速为1 500 hops/s,信号带宽为2 000 kHz的跳频信号进行仿真,其中信噪比为-6 dB。

图7 仿真结果

图7中(a)为信号的初始SPWVD图像,可以看出含有大量噪点。图7(b)为去噪后的时频分布,对比初始状态,噪声去除效果较好。图7(c)为阈值分割后的时频分布,此时信号分布中各细节特性更加凸显,但时频分布较宽。图7(d)是OPTA细化处理后的结果,此时图像脊线的宽度变成近似单像素宽。

5 结论

以跳频信号为研究对象,抽取信号的SPWVD图像,并依次进行形态滤波、阈值分割以及 OPTA细化对时频图像进行优化。仿真结果表明文中方法能够对跳频信号的时频分布进行有效降噪及细化,为后续信号参数的准确估计提供有利条件。