扩展多约束最优制导律特性及其应用*

2019-06-24马婷婷刁兆师魏钰良

弹箭与制导学报 2019年6期

马婷婷,刁兆师,魏钰良,何婷

(1 北京控制工程研究所,北京 100190;2 中国兵器工业导航与控制技术研究所, 北京 100094)

0 引言

随着现代化作战任务变化和精确制导弹药技术快速发展,为更好地发挥战斗部威力,针对多约束制导律的研究具有很大实际工程价值。

针对不同应用对象,根据多种理论方法提出了多种带终端角度约束的制导律[1]。迄今研究较为深入、应用较为广泛的是基于最优控制依据不同期望指标获得不同形式的带多约束制导律。带终端角度约束制导相关理论成果于1969年在Apollo飞船月球表面垂直着陆得到应用[2],Kim和Grider于1973年较早地提出带落角约束最优制导律问题[3],自此开始该课题一直吸引着专家学者的关注,并取得许多成果。Zarchan[3]应用施瓦茨(Schwarz)不等式详细地推导了弹道成型制导律,并解析分析了角度约束和确定性误差干扰对过载指令的影响。Ben-Asher等[4]研究表明弹道成型制导律有利于降低对剩余时间估计偏差的敏感度。Ryoo等[5-6]后续研究了考虑动力学滞后的制导系统特性以及剩余飞行时间估计问题。常超、祁载康等[7]研究了系统滞后及阶次对位置脱靶量和角度脱靶量的影响。Ohlmeyer等[8]以剩余飞行时间幂函数的倒数为最优目标罚函数的权重,最早推导了广义矢量最优制导律,推广了传统弹道成型制导律。刘大卫等[9]采用施瓦茨不等式推导了广义弹道成型制导律,研究了一阶动力学滞后系统的位置和角度脱靶量特性,并给出可用过载限制的导引系数设计方法。王辉等[10-11]求解得到了由初始位置误差、方向误差、目标机动及角度约束引起的加速度指令解析解,研究了一阶动力学滞后制导系统的无量纲位置脱靶量和角度脱靶量特性。温求遒等[12]基于线性二次最优控制推导了扩展多约束制导律;通过无量纲化加速度指令变化规律分析,提出了制导初始条件设计方法及最大需用过载估计方法。张文渊等[13]推导了含一阶动力学滞后的多约束最优制导律,研究了导引头隔离度和制导参数对稳定性及制导性能的影响。

在上述文献基础上,文中进一步深入研究了扩展多约束制导律的无量纲化加速度指令特性,同时推导了相应视线角变化的解析解并分析了无量纲化视线角变化特性。最后仿真验证了相关解析结论的有效性。

1 扩展多约束最优制导律

将导弹控制系统视为理想环节,在小角度假设下导弹-目标相对运动几何关系的简化线性模型如图1所示[2],其中:at是目标常值机动加速度,ac是导弹加速度指令。

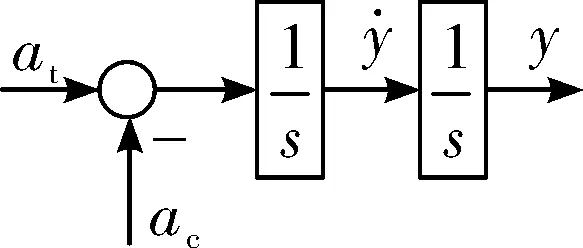
图1 制导律简化模型

将图1模型写成状态方程形式为

(1)

带终端落角约束问题可转化为终端约束最优控制问题[2],其最优目标罚函数为:

(2)

对应终端约束条件为:

其中,R(t)为正定时变权函数,其定义为:

(3)

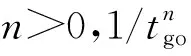
(4)

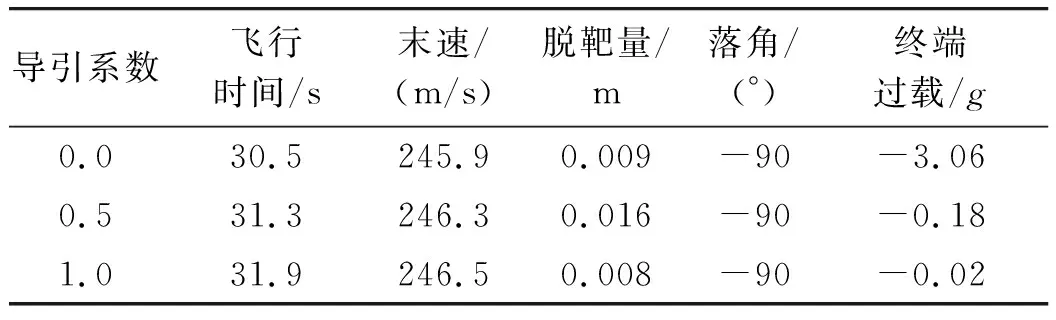
式中:Np=2(n+2),Nλ=(n+1)(n+2),Nt=(n+2)(1-n)/2。经典比例制导律经验导引系数Np取值为3～6,且最优控制器往往增益太高、带宽过高,引起系统失稳[14],因此对应n有效取值范围为n∈[0,1]。表1给出了3组典型导引系数。

表1 扩展多约束最优制导律典型导引系数

2 最优制导律特性分析

掌握不同确定性误差及约束因素下的弹道解析特性,尤其是需用过载和视线角变化趋势,将非常有助于总体方案设计和指标论证,其确定性误差包括初始位置误差、初始瞄准方向误差、目标机动3项,约束是指终端落角约束。

2.1 加速度指令变化

按照文献[2,10]中最优制导律的解析加速度指令表达式为:

(5)

令导弹初始瞄准方向角误差为β0,小角度假设下有：

(6)

根据视线角几何关系有λ=y/r=y/(vctgo),对该式求导得：

(7)

进一步整理得:

(8)

因此可知加速度指令式(5)右侧各项为误差扰动或约束的所需加速度分量,即

ac(t)=a(t)|y(0)+a(t)|β0+a(t)|λf+a(t)|at

(9)

(10)

(11)

(12)

(13)

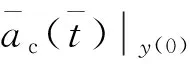
(14)

(15)

(16)

(17)

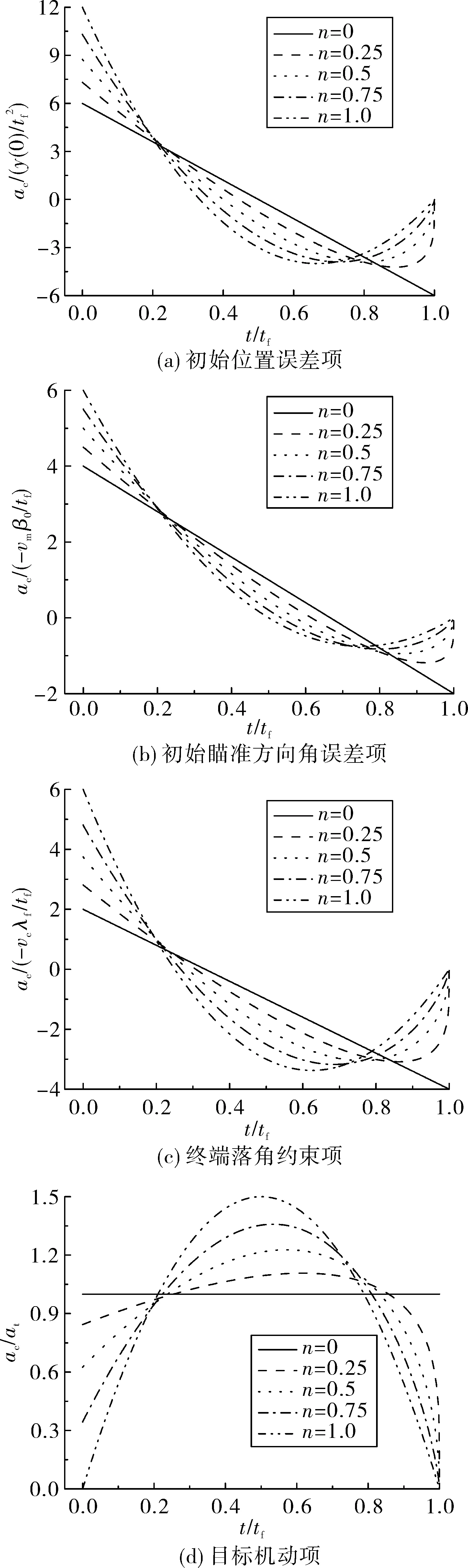
另外,由图2知对于n不同取值,无量纲化加速度曲线相交于t1(0.2tf附近)和t2(0.8tf附近)。初始位置误差、瞄准误差以及终端落角约束的无量纲化加速度变化趋势随n变化一致,当tt2,无量纲化加速度随n的增大而减小。目标机动的无量纲化加速度变化趋势与上述相反。

图2 无量纲加速度变化趋势

2.2 视线角变化

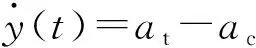
(18)

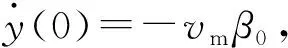
(19)

(20)

(21)

对式(19)～式(22)再次积分可得:

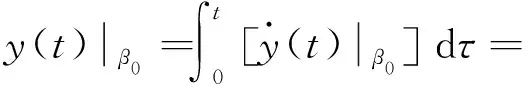
(24)

(25)

(26)

由各项引起的视线角变化表达式分别为:

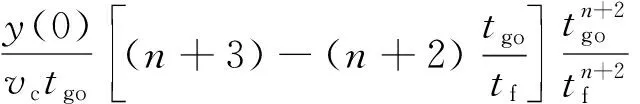
(27)

(28)

(29)

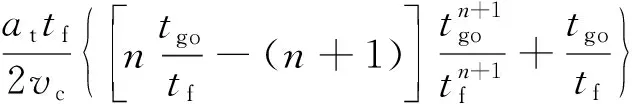
(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

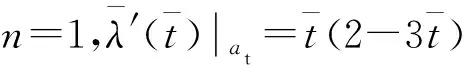
另外,由图3看出,对于初始位置误差、瞄准误差引起的无量纲化视线角变化趋势一致,随着n增大,曲线上拉，更快趋于0;终端落角约束引起的无量纲化视线角曲线随着n增大而下拉,更快趋于1;而目标机动引起的无量纲化视线角曲线随着n增大而下拉,放慢趋于0。

图3中无量纲化视线角均大于零,说明4个因素的极性将直接影响视线角变化趋势。若瞄准角误差β0与终端期望落角λf极性相反,前者引起的视线角变化趋势与后者的变化趋势一致,有利于弹道成型。因此,中制导方案设计最好要保证在转到多约束制导律时瞄准角误差β0与终端期望落角λf极性相反。若目标机动at与终端期望落角λf极性相同,前者引起的视线角变化趋势与后者的变化趋势一致,有利于弹道成型。

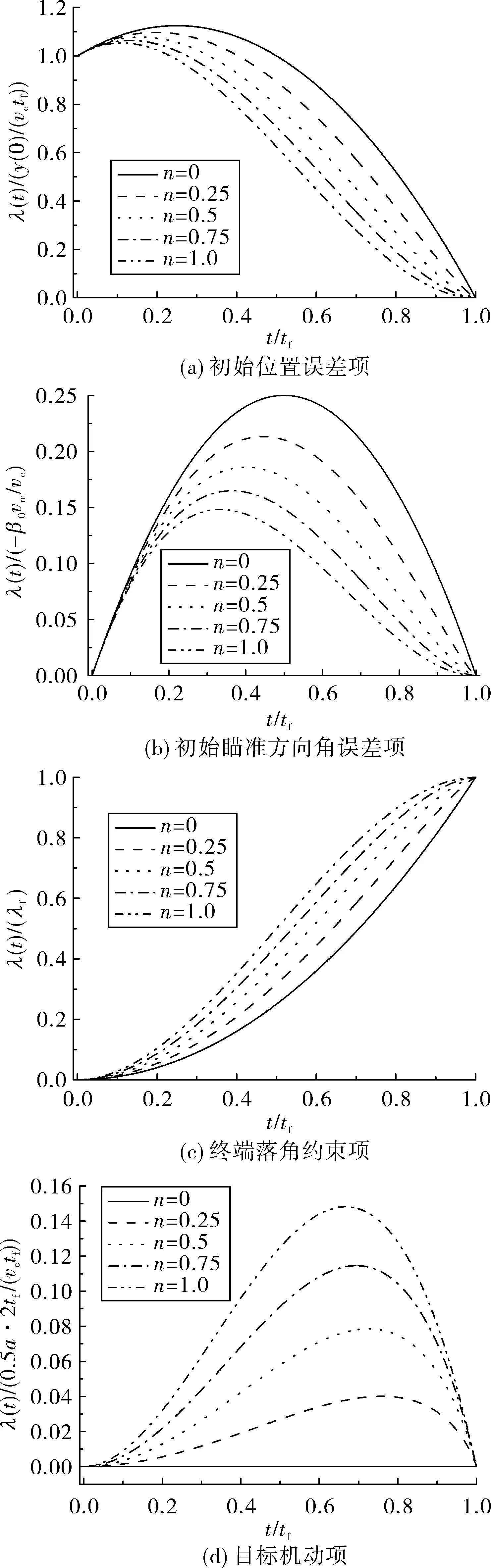
图3 无量纲视线角变化趋势

3 工程化应用准则

对于战术导弹末制导阶段，导弹-静止目标相对运动几何关系如图4。图中,r、λ、θ分别表示弹目相对距离、视线角、弹道倾角。对于打击静止目标,终端视线角λf=θf[15]。则视线角变化量为λ*f=λf-λ0,初始瞄准方向角误差量为β0=θ0-λ0。

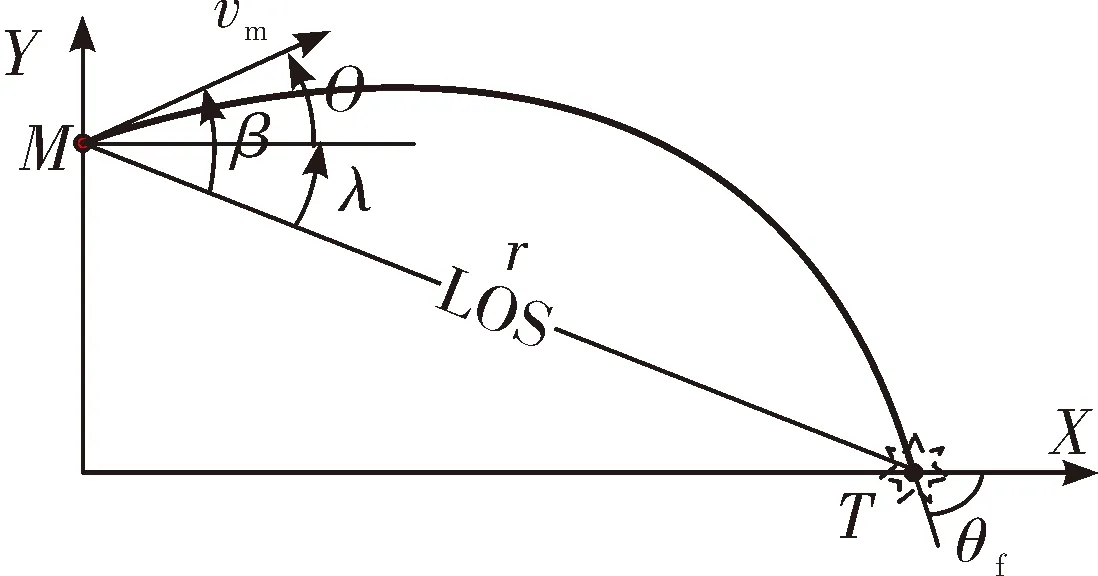
图4 弹目相对运动几何关系

由式(9)～式(13)、无量纲化加速度因子和y(0)=0得:

(39)

(40)

式中:at是由作用在导弹上的重力等效而来[2],其大小为at=gcosθ,飞行时间tf可由r/vc近似估计。

令导弹可用过载为ap,启动时刻需要满足

(41)

(42)

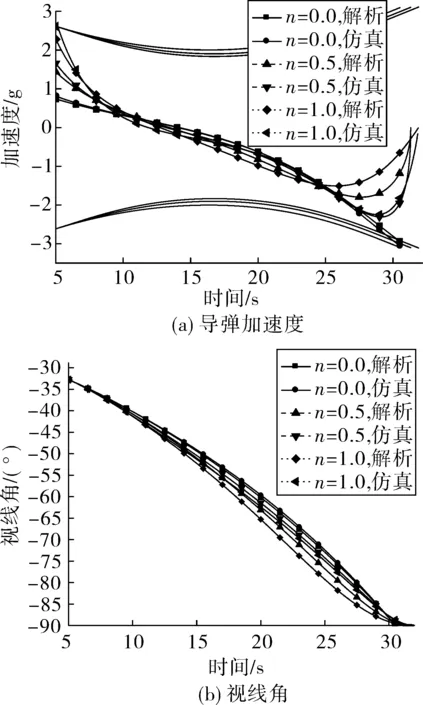
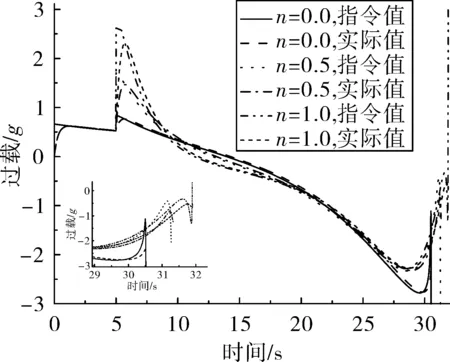
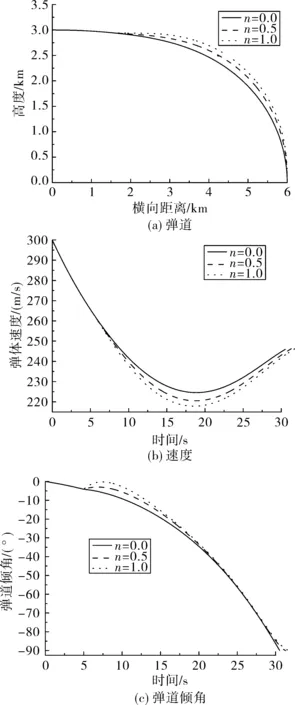
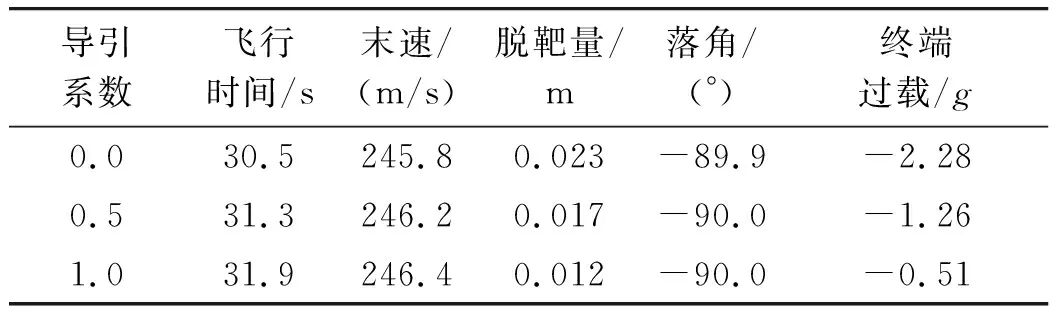
经过分析可得，当0

(43)

考虑控制系统动力学滞后,为保证位置脱靶量和终端角度要求,飞行时间tf应大于控制系统响应时间的15～16倍[10,12],即tf≥(15～16)Tm,可转化为弹目距离

r0≥vctf

(44)

(45)

以下3个要素可作为末制导设计的参考准则:

①适当的中制导来保证瞄准方向角误差和视线角变化量控制在一定范围内,保证式(41)、式(45)成立;

②选取适当大的制导时间tf满足式(44),并保证式(41)、式(45)成立,可用过载留有一定裕量;

③若期望终端加速度收敛于零,选取导引系数n>0;同时,导引系数n保证式(41)、式(45)成立。

4 数学仿真

以航空制导弹药纵向平面运动为例进行数学仿真，验证上述设计原则的有效性,该弹药无动力,经过稳定、适当中制导进入末制导段完成垂直攻击任务,初始条件及终端约束要求为:初始高度为Hm=3 km、初始速度vm=300 m/s、弹目水平距离x=6 km、水平投弹θm=0°、期望落角θf=-90°。

取表1扩展多约束最优制导律典型导引系数来进行数学仿真,其结果见表2,弹道曲线如图5。由表2知,上述典型导引系数均可达到期望脱靶量和期望落角要求,且终端速度散布很小,说明n在[0,1]上取值对终端速度影响不大;当n=0.5、n=1.0时,终端过载接近为零,与解析结论一致,有利于终端攻角收敛,避免大攻角“跳弹”发生。

另外,由图6(a)知：解析与仿真所需加速度指令变化趋势基本一致,当n=0时,加速度指令单调递减;当0

表2 理想情况仿真结果

图5 仿真曲线

考虑控制系统滞后,令控制系统响应时间Tm=0.3 s进行仿真,其结果见表3,其加速度指令与实际值见图7。从表2与表3对比可以看出，控制系统滞后对飞行时间、末速、脱靶量、落角影响不大,但对终端过载影响严重,违背攻角收敛要求;结合图7知,其原因是在滞后影响下在接近目标时加速度指令存在半震荡甚至发散现象。因此实际工程应用时必须对终端加速度指令采取必要措施,如终端加速度指令归零等。