成都地震台测震记录中干扰特征的研究
2019-06-21何思源徐文海李贵元
林 建,何思源,徐文海,李贵元
(成都地震基准台,四川 成都 611730)
0 引言
成都地震台台址所处的走石山是白垩系砾岩经风化剥蚀后形成,基岩很不完整,发育多层溶洞,部分已被风化黄土所充填。台址基岩属白垩系底部砾岩,摆墩处的基岩比较破碎。台址的优劣将直接决定台站产出数据的质量[1],破碎的台基对测震记录的影响是明显的,而干扰的增多对于测震记录的质量更是雪上加霜。文中运用希尔伯特-黄变换、小波变换、傅里叶变换对成都地震台测震记录进行分析,在分析过程中可以更加全面地了解成都地震台测震记录中干扰的特征。
1 数据截取长短对波形分析的影响
天然地震事件由于震级、震中距、发震机制的不同,地震计记录到的波形数据的长短也有所不同。为了获得地震事件的完整波形,所截取的时间长度必然也有所不同。
根据Hilbert边际谱:

可知数据截取的时间长短对于Hilbert边际谱是有影响的,而这个影响具体有多大,需要进行分析与讨论。文中选取成都地震台JCZ-1T地震计所记录的2017年8月9日20点03分发生的九寨沟地震(M3.1)作为分析实例。分别截取记录长度为150 s、250 s、300 s的波形片段,每个波形片段内均包含了九寨沟地震(M3.1),如图1所示。随后,对不同截取时间长度的波形数据进行Hilbert边际谱的求取。由图2可知,截取时间长度为150 s、250 s、300 s的Hilbert边际谱内基本形态是保持一致的,主体范围的幅值也是一致的,只是在端点附近的幅值有所差异。可见数据截取的时间长度不同仅对端点附近的幅值有所影响,对于地震事件中主要的频谱范围及幅值的大小并没有明显的影响。因此,经过上述分析,可知数据截取长短的不同并不影响对主体范围内频谱特征的判定。
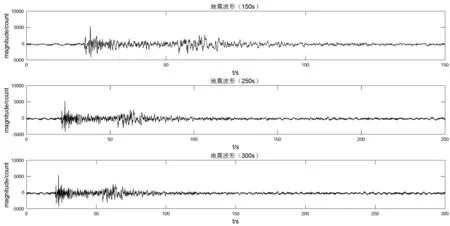
图1 不同截取时间长度的地震波形数据Fig.1 Seismic wave data of different lengths of time
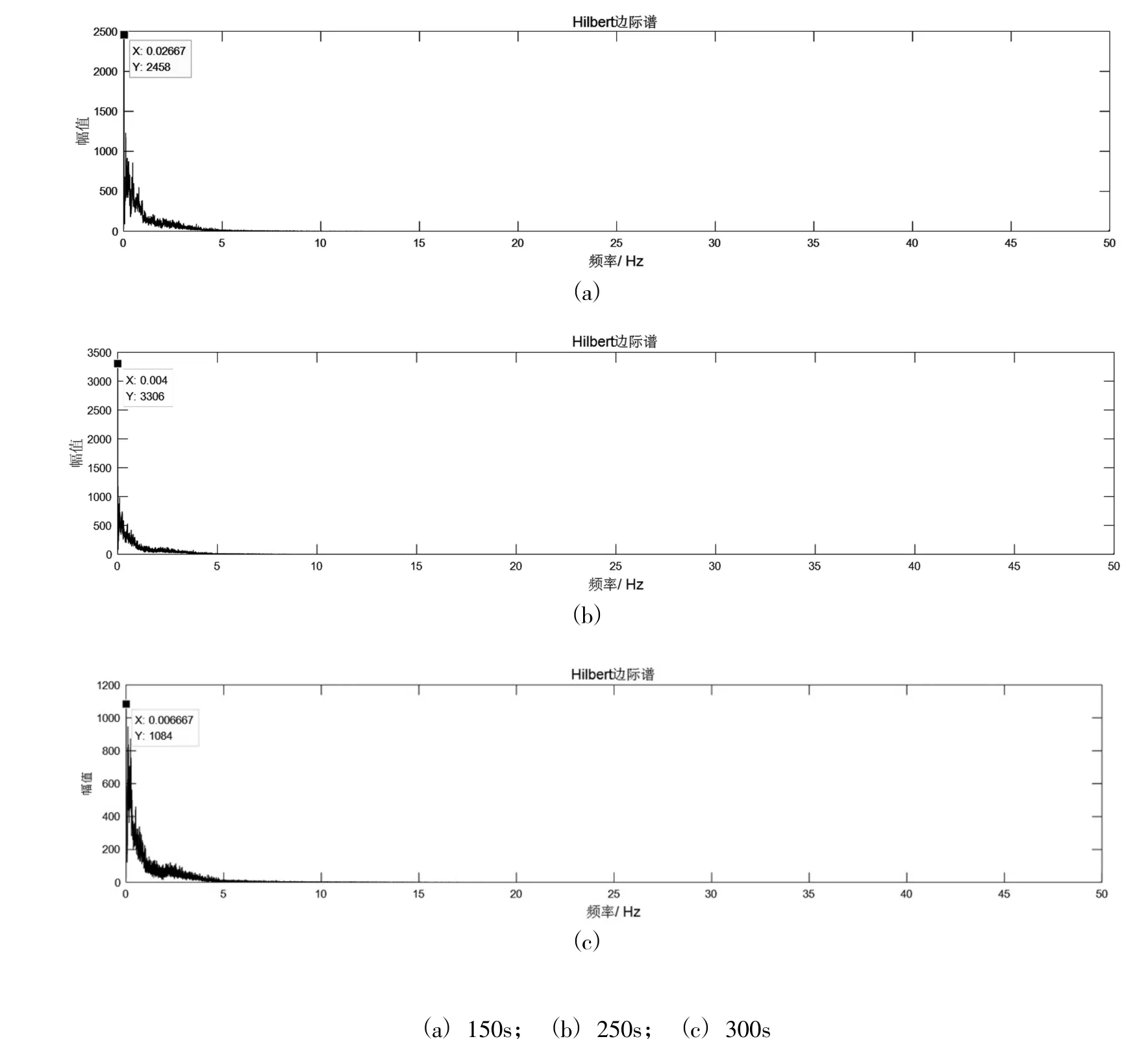
图2 不同截取时间长度的Hilbert边际谱Fig.2 Hilbert marginal spectrum of different lengths of time
2 成都地震台测震记录特征的分析
成都地震台目前使用了两套超宽频带地震计JCZ-1型和JCZ-1T型,配套的数据采集器是EDAS-24IP型。其中JCZ-1是分体装置,由一个垂向和两个水平向地震计构成,频带为20Hz~DC,JCZ-1T型是JCZ-1型的改进型,是三分量一体机,带宽为 50Hz~DC[2]。JCZ-1T 除了带宽与JCZ-1不同,其它设计基本一致。
JCZ-1与JCZ-1T地震计均具有良好的机械弹性结构,具有以下的特征[3]:
(1)低噪声;
(2)高的寄生共振频率;
(3)良好的工艺性。
仪器具有高灵敏度、低噪声特点,动态范围大于140dB。地震计采用力平衡式的负反馈系统,传递函数稳定,具有密封、磁屏蔽和高精度恒温功能的环境保护装置,有效地抑制了大气压力、外部磁场及温度变化对仪器的影响,使地震计在超低频端也能稳定工作。JCZ-1、JCZ-1T地震计也是目前少有的周期为360 s的地震计,其它台站大多为周期120 s的地震计。JCZ-1、JCZ-1T地震计记录的范围更广,记录的测震资料也更加准确、详尽,因此本文采用了JCZ-1、JCZ-1T地震计所记录的测震资料作为研究对象。
在对成都地震台JCZ-1、JCZ-1T地震计记录的测震数据的分析过程中,发现绝大多数中小震级的地震波形均受到了严重的干扰。下面用一个近震实例进行分析说明。近震选取的是2016年07月27日19时59分记录于JCZ-1T的四川平武ML2.5级地震(垂直分向)。由图3可知,波形记录受到了严重的 “波形毛刺”干扰。这些复杂的干扰使得地震的震相被淹没,难以准确地从中获得地震事件的信息。
为了分析波形数据中不同时间、不同频率地震信号强度的分布情况,我们对波形数据采用Hilbert-Huang变换和小波变换,求得Hilbert-Huang时频图和小波时频图。由图4、图5可知,信号强度从20 s附近开始增强,这和平武地震Pg波到达的时间吻合。20~60 s信号强度最为集中,这是由于这个时间区间包含了平武地震波形的信号。根据时频图可知,波形的整个频率范围是集中在0~25 Hz内,超过25 Hz后基本没有信号强度的分布。其中,信号强度在0~5Hz最为集中,5~10Hz次之,10Hz之后便逐渐减弱了。通过对地震波形进行快速傅里叶变换以及求Hilbert边际谱,得到FFT频谱图以及Hilbert边际谱。由图6、图7可知,0~5 Hz的幅值最高,5~10 Hz次之,10 Hz后幅值逐渐减小,与Hilbert-Huang时频图、小波时频图所得到的结果是一致的。
值得注意的是,FFT频谱图与Hilbert边际谱中均存在2~4 Hz高幅值的频率范围,而速度功率谱估计中(图8)同样存在2~4 Hz高幅值的频率范围。这表明2~4 Hz是一个客观存在的频率范围。
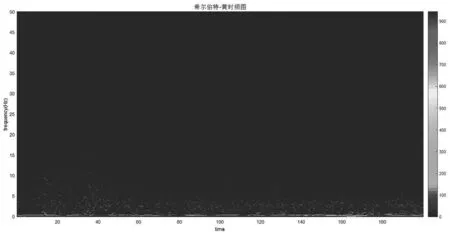
图4 Hilbert-Huang时频图Fig.4 Time-frequency diagram of HHT
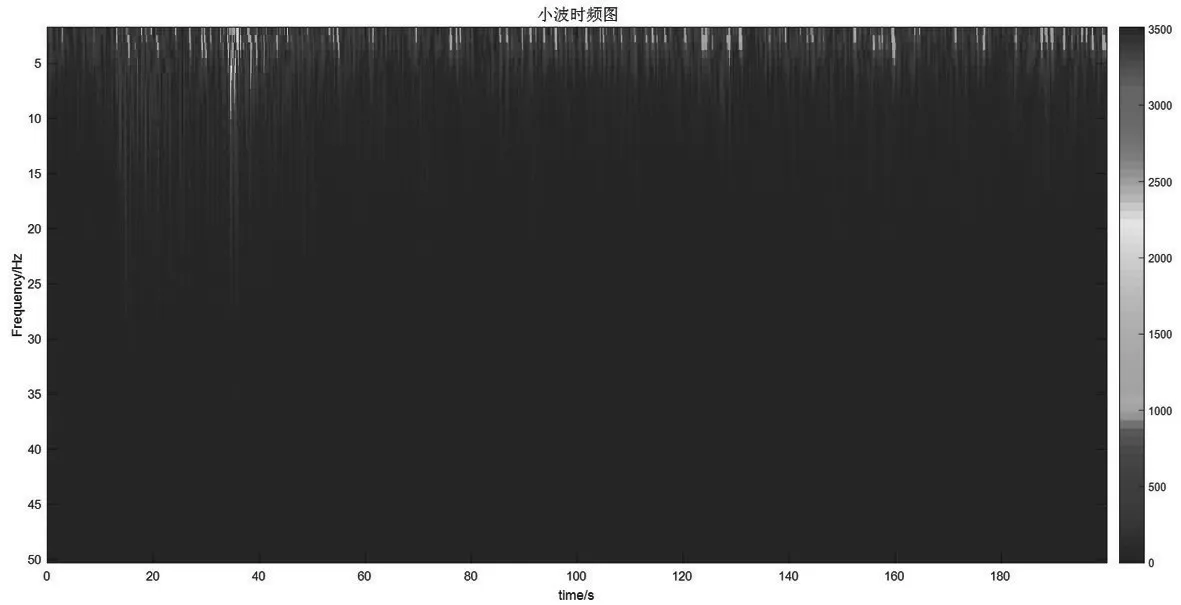
图5 小波时频图Fig.5 Time-frequency diagram of Wavelet transform
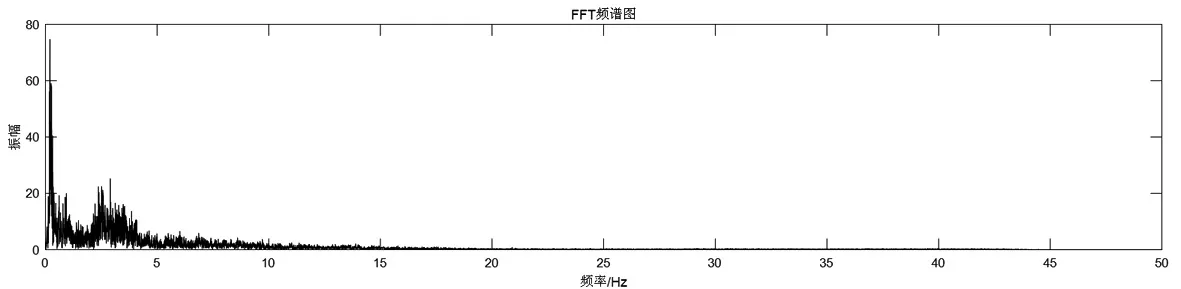
图6 FFT频谱图Fig.6 FFT spectrum
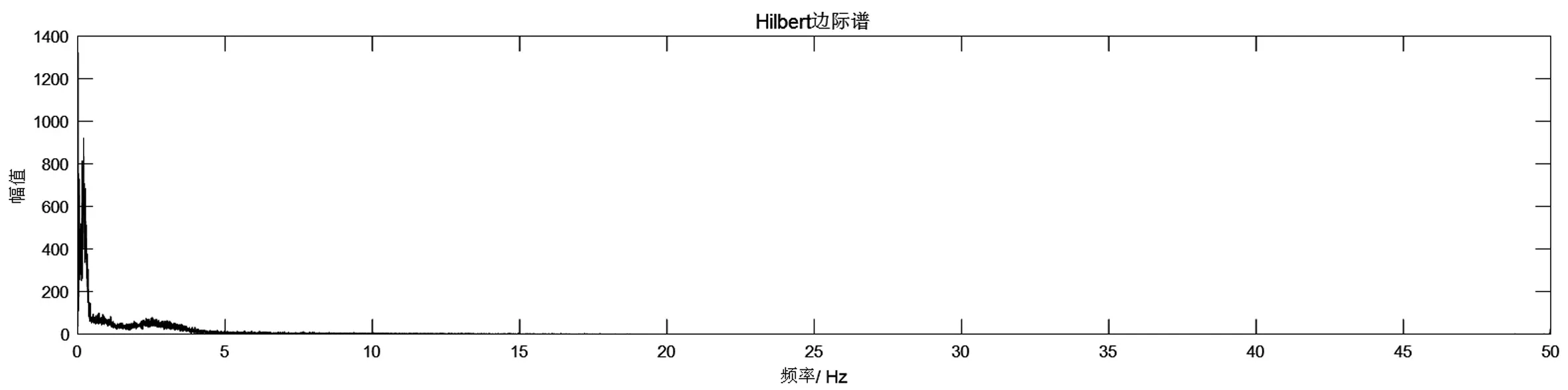
图7 Hilbert边际谱Fig.7 Hilbert marginal spectrum
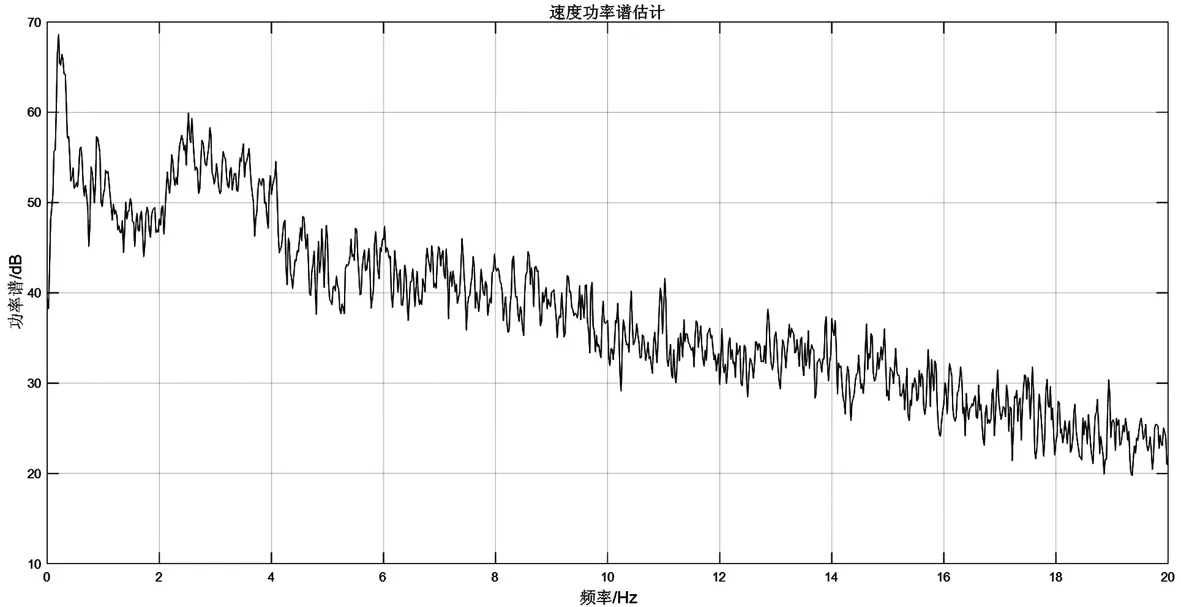
图8 速度功率谱估计Fig.8 Power spectrum of Velocity
为了对2~4 Hz的频率范围进行定义,文中通过IIR带阻滤波器分别对地震波形以及背景噪声中的2~4 Hz频率范围进行带阻滤波。由图9可知,平武地震波形中的“毛刺”干扰在滤除2~4 Hz频率范围后得到了明显的改善,而地震波形的整体形态以及振幅并没有受到影响。同时,背景噪声的波形在滤除2~4 Hz频率范围后,干扰也被明显地压制。这证明平武地震波形中存在的2~4 Hz正是原始波形中“毛刺”干扰的频率范围。
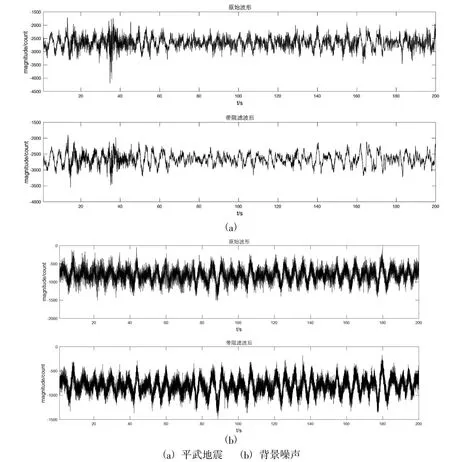
图9 滤除2~4Hz频率范围前后的地震波形Fig.9 Seismic waveform before and after 2~4Hz were filtered out
3 干扰的分布特征
首先,需要讨论的是2~4 Hz干扰频率范围在JCZ-1记录的地震波形中的存在性。文中选取了JCZ-1在2016年7月27日19时59分与JCZ-1T同一时刻记录的四川平武ML2.5级地震的波形进行对比研究。运用快速傅里叶变换分别求取FFT频谱图,并进行频谱对比(图10)。由对比结果可知:两套仪器同时记录的平武地震的波形中均存在2~4 Hz干扰。JCZ-1和JCZ-1T在10 Hz之前的频谱基本保持一致,而在10 Hz之后,JCZ-1相比JCZ-1T出现了更多的高频,从10 Hz一直持续到45 Hz。其中,25~45 Hz频率范围的幅值存在明显增大的情况。这说明JCZ-1地震计在高频端的噪声比JCZ-1T更多且幅度更大[4]。由于两台地震计是处于同一台基以及同一摆墩,因此JCZ-1出现的高频应该与仪器自身有关。两套地震计记录的同一地震的频谱内均出现了2~4 Hz干扰。
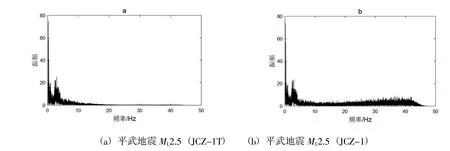
图10 JCZ-1T、JCZ-1记录的地震事件频谱图Fig.10 Seismic event spectra recorded by JCZ-1t and JCZ-1
通过上面的研究,可知JCZ-1、JCZ-1T地震计记录的地震波形均会出现2~4Hz的干扰。这里需要提出一个疑问:2~4Hz干扰频率范围是否为成都地震台测震记录中的普遍性干扰?
为了解答这个问题,本文随机选取了JCZ-1、JCZ-1T分别记录的2013—2018年40个地震事件的地震波形,对每个地震事件的波形做波形分析,并记录下分析结果。通过分析发现:选取的2013—2018年40个地震事件中27个存在明显的2~4 Hz干扰(表1)。而干扰频率是否明显与成都地震台记录的地震震中距以及震级有关:成都地震台记录的震级6级及以上的远震、震级5级上下的近震以及震级5级上下且震中距15°左右的远震并未出现明显的2~4 Hz干扰;震级5.5级及以下且震中距大于20°的远震、震级4.5级及以下的近震更容易出现明显的2~4 Hz干扰,这也符合成都台中小震级的地震受干扰明显的现况。上述研究结果表明:2~4 Hz的干扰并非少数地震的特例,是普遍存在于成都地震台中小震级的地震事件记录中的。
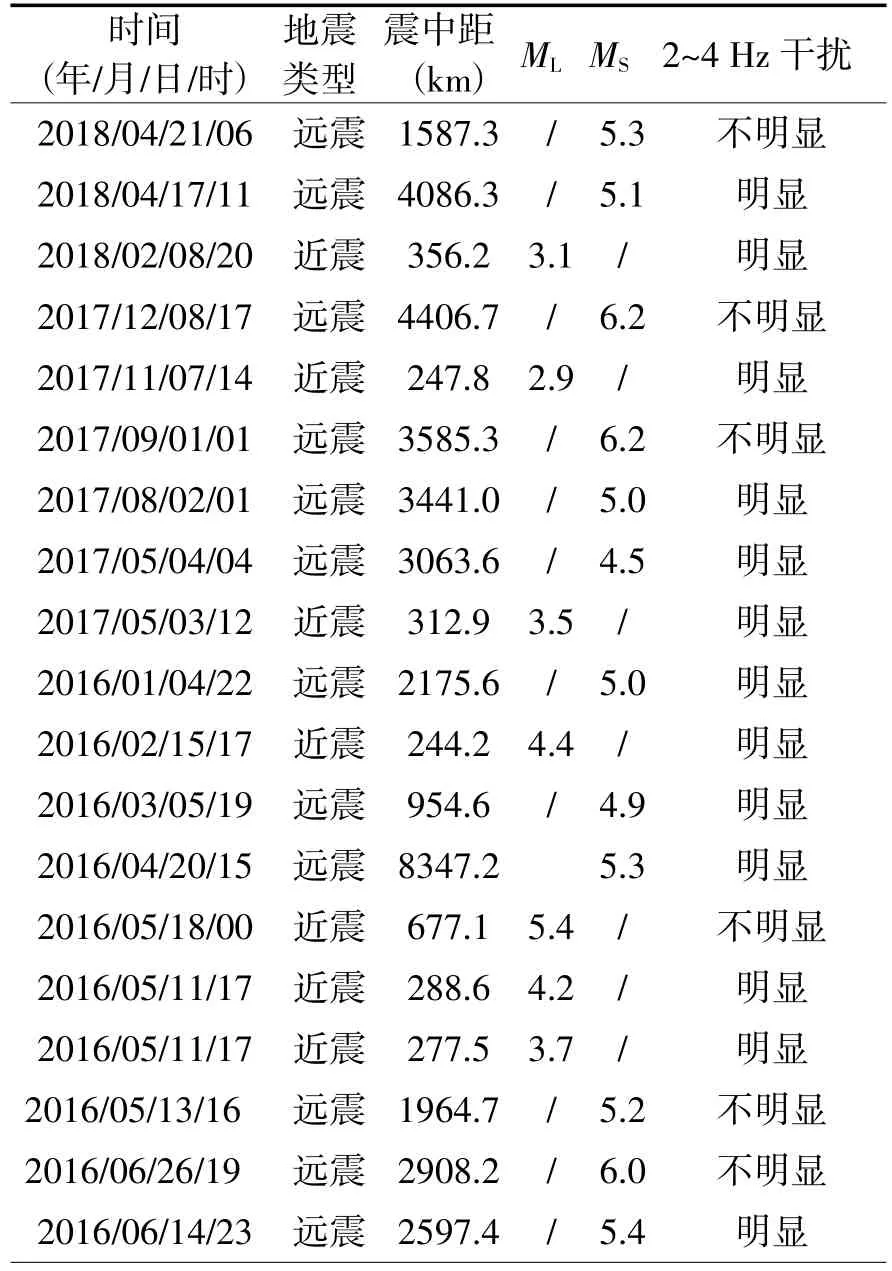
表1 地震事件受2~4 Hz干扰情况的分析结果(JCZ-1T、JCZ-1)
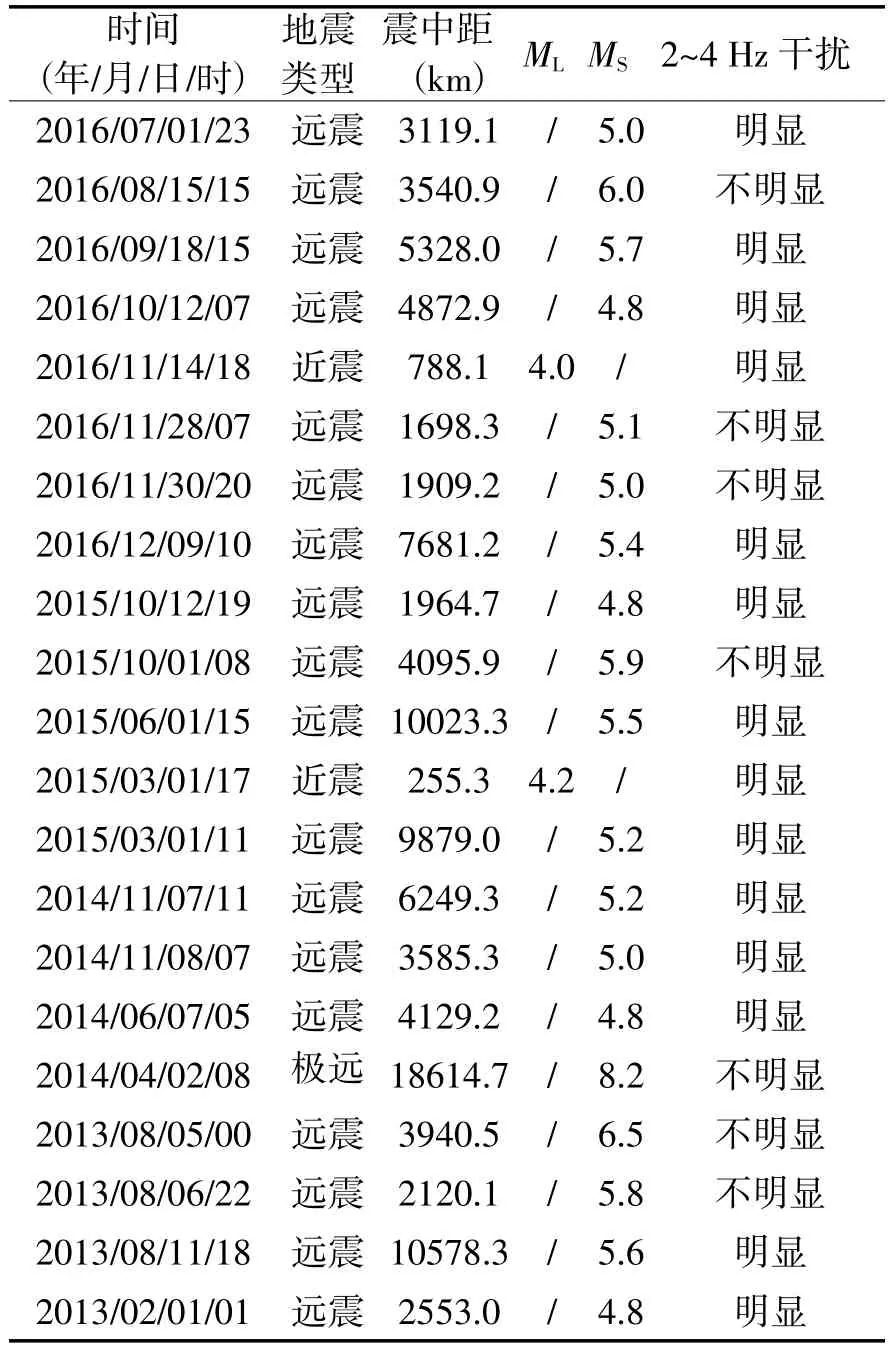
续表
4 成都地震台的仪器响应
当地震台站的地震计接收到地震波时,摆针发出振动,并将这些振动进行记录。地震计记录的地面运动记录可以表示为u(t):

其中 s(t)代表震源项,g(t)代表路径效应,i(t)代表仪器响应,*代表卷积。台站记录的地震波形记录是震源项、路径项以及仪器响应三者卷积得到的。
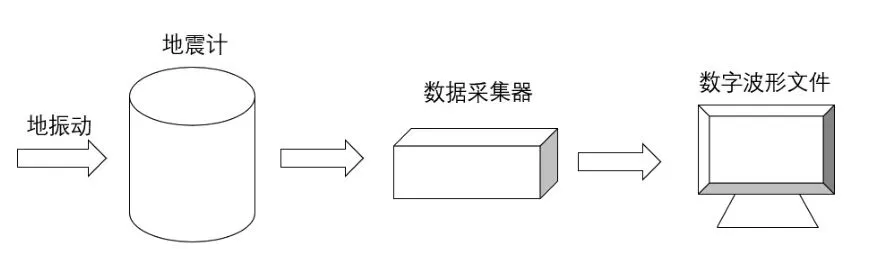
图11 地震仪系统接收和输出地振动信号的过程Fig.11 Process of receiving and sending ground vibration signal
地振动信号被地震计响应转换为电压模拟信号,电压模拟信号又输入到数字采集器进行数字采集和转换,之后输出数字地震信号给计算机进行处理、分析和存储。在这一过程中,模拟信号的响应函数用Laplace(拉氏)变换表示为:

其中,s=i2πf。频率响应可表示为:

其中,R(f)是频率的函数。在某个特定的频率 fs,有即 R(f)在频率 fs处归一化,Sd1是放大系数,R(f)又可表示为:

式中HP(S)是零极点表示的transfer函数,A0是归一化系数,即A0使得其它各频率成分信号的响应R就是标准1的相对值。
第一个阶段主要功能是将检测到的地震信号(速度)转换为电压模拟信号,并进行电压放大。因而这个阶段的输入单位是m/s,输出单位是伏特(V)。这阶段的响应函数可以表示为:

在数采中,是将电压模拟信号转化为数字信号的过程。其中有两大步骤:第一步,是将上个阶段产生的电压信号转换为离散的电压信号,输入的单位是伏特V,输出单位是counts,这个过程中,所有频段内的振幅响应是一致的,也就是只存在唯一放大系数Sd2,并可能存在一个时间延迟;第二步,对离散数据进行处理,这个过程又包含了三个小部分:离散信号滤波、数据重采样和校正滤波引入的时间延迟。也就是说,这个阶段需要考虑的就只是放大系数,归一化因子可以忽略,或可当作是1.0。同样的,新的响应函数不会参与到数据重采样以及时间校正的过程当中,虽然一般滤波器的响应函数会在Nyquist频率附近产生5%左右的震荡,但我们关心的频率是远远小于Nyquist频率的,因此可以忽略滤波器的响应函数带来的影响。整个仪器响应过程中,第一个阶段最为复杂,需要给出放大系数Sd1、归一化因子A0以及多个零极点;第二和第三个阶段只需要给出放大系数Sd2和Sd3就可以了。
仪器响应最终可表示为:
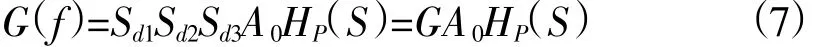
即需要仪器在第一个阶段的零极点信息、归一化因子A0以及整个仪器响应过程的放大系数,整个仪器响应过程的放大系数可看作为常数G。
了解到仪器响应特点后,我们通过RESP文件对数据进行“去仪器响应”处理,并得到地面的原始运动。再对去仪器响应后的波形做带通滤波,压制低频和高频,并与原始波形进行对比。这里我们选用的待处理数据是JCZ-1T记录的阿拉斯加地震波形数据。由图12和图13所示,去除仪器响应得到地面原始运动后,波形仍然存在2~4 Hz干扰。将去除仪器响应前后的波形做FFT频谱分析对比,得到的结果显示:2~4 Hz干扰并未与仪器响应一同去除。这说明了干扰与仪器响应无直接关联性,需要对干扰产生的原因进行更深入的探究。
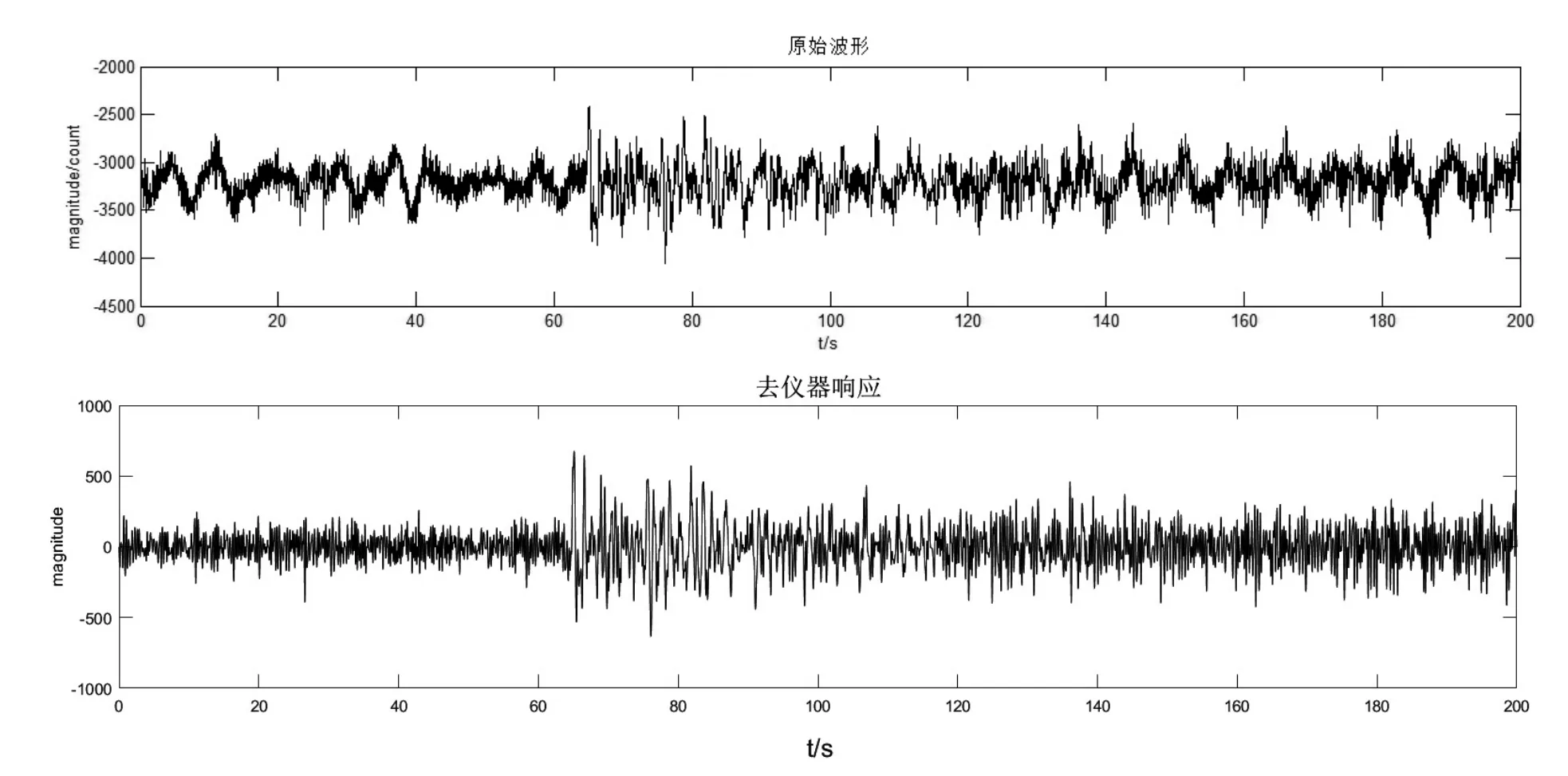
图12 去仪器响应前后波形对比Fig.12 Comparison of waveform before and after the instrument response removal
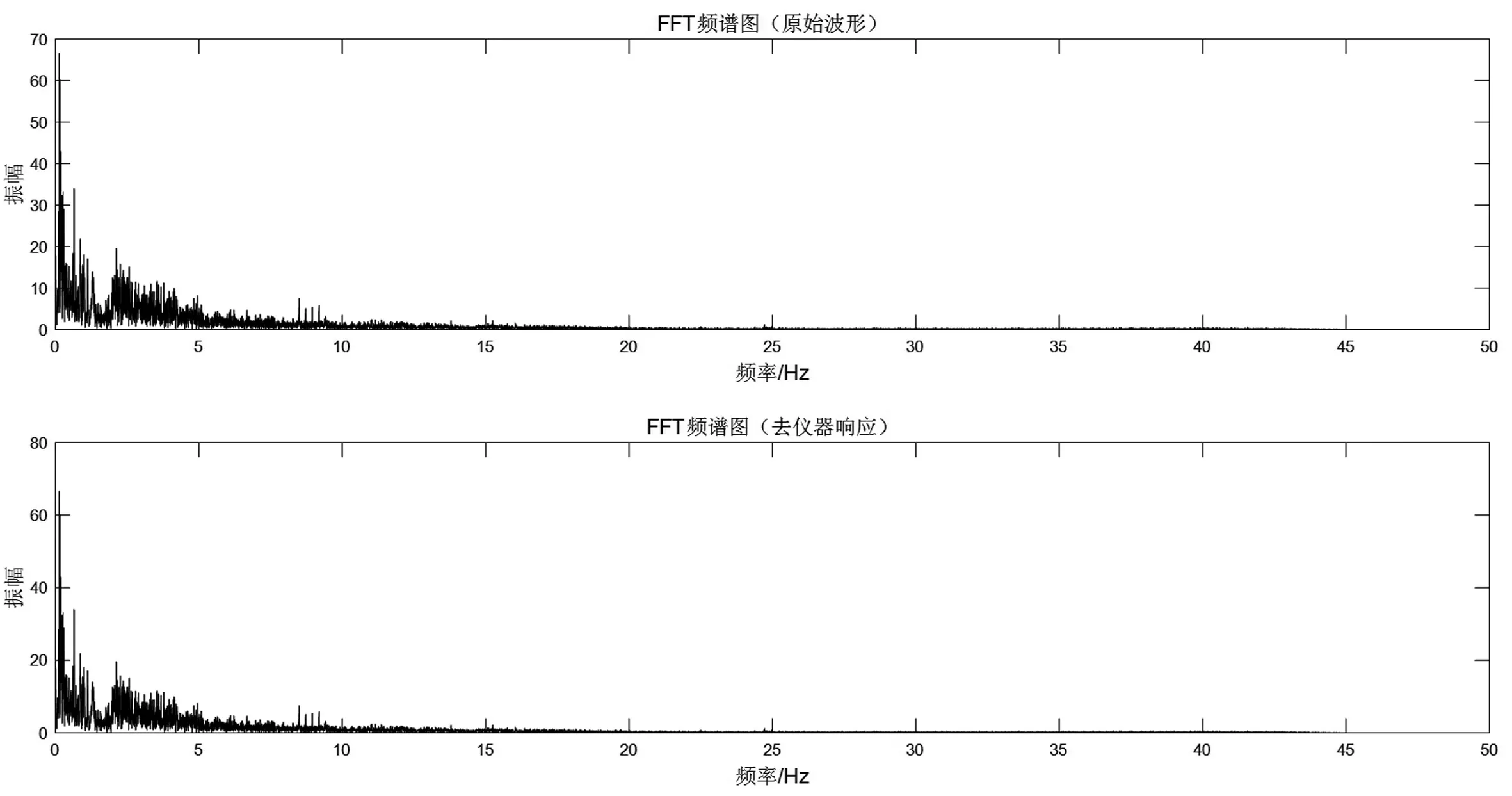
图13 去仪器响应前后频谱对比Fig.13 Comparison of waveform spectrum before and after the instrument response removal
5 结论与讨论
通过文中的研究,可以得到以下结论:
(1)2~4 Hz干扰对成都地震台测震记录的质量造成了严重的影响,在波形中的宏观表现为“波形毛刺”,已成为成都地震台测震记录中的普遍性干扰。
(2)JCZ-1地震计、JCZ-1T地震计记录的波形中均存在2~4 Hz干扰。其中,JCZ-1地震计或由于仪器自身因素,使得其在高频端的噪声比JCZ-1T更多且幅度更大。
(3)2~4 Hz干扰的分布与成都地震台记录的地震震中距以及震级有关,在震级5.5级及以下且震中距大于20°的远震、震级4.5级及以下的近震更容易出现明显的2~4 Hz干扰频率范围,即普遍存在于成都地震台中小震级的地震事件记录中。
(4)2~4 Hz干扰与仪器响应之间并无直接的相关性。
(5)干扰产生的原因还需要进一步的研究。后续将通过对成都地震台近15年的数据进行采样分析,得出干扰出现的时间范围以及干扰的演变过程,结合仪器自身的属性、台基历年背景噪声进行综合讨论。
