基于弯曲和径向疲劳试验的车轮仿真分析
2019-06-21孙跃,孙圆
孙 跃,孙 圆
1.江苏大学东海机械汽配研究院,江苏 连云港 222000;2.卓郎(江苏)纺织机械有限公司,江苏 常州 213200
车轮是汽车的一个重要的安全部件,起着承载、传递、驱动和制动的作用。汽车在行驶过程中受到外部随机动载荷影响,应力值一般低于材料的强度极限,但会发生疲劳断裂,国内外的相关研究也证实了这一点[1]。弯曲疲劳试验、径向疲劳试验和冲击试验是汽车车轮最主要的三大性能试验,我国国家标准、SAE标准等都对此作了详细的技术要求。过去通常依靠试验和经验类比的方法对车轮的疲劳寿命进行预测,但随着市场对车轮更新和需求量的日益增大,这种周期长、成本高的产品开发模式和产品外观雷同的缺点越难以满足整车企业的要求。因此在车轮研发阶段,运用CAE技术,采用有限元分析方法,预测车轮的疲劳寿命,能够有效提高设计效率、缩短研发周期。
本文基于材料的S-N曲线,根据国家标准GB/T 5334—2005《乘用车车轮性能要求和试验方法》[2]的要求,利用ANSYS Workbench软件对A356材质的铝合金车轮的弯曲疲劳试验和径向疲劳试验进行仿真分析,预测疲劳裂纹位置,估算车轮疲劳寿命。其中,弯曲疲劳仿真模拟物理试验,利用加载轴进行加载;径向疲劳仿真基于Stearns等[3]的研究成果,考虑充气压力和轮胎材料复杂性的影响,简化轮胎建模,进行等效加载。
1 车轮疲劳试验
1.1 弯曲疲劳试验
车轮弯曲疲劳试验将车轮的轮缘用夹具固定在试验台上,用螺栓将加载轴一端和车轮连接,对加载轴另一端施加一个大小恒定、方向沿周向变化的力,模拟车轮在承受一定载重后一直在转弯行驶。车轮在整个试验过程中承受弯曲载荷作用,直至车轮出现新可见裂纹,或者加载点的偏移量超过初始完全加载时偏移量的20%,则认为车轮已失效。试验原理如图1所示。

图1 弯曲疲劳试验示意图Fig.1 Schematic diagram of bending fatigue test
1.2 径向疲劳试验
车轮径向疲劳试验是对车轮承受一定载重后在平直道路上行驶情况的模拟,试验原理如图2所示。试验装置包括一转鼓、车轮安装座和液压缸。转鼓表面光滑且能恒速旋转,其宽度大于试验轮胎总宽度;车轮安装座安装在直线导轨上,在液压缸作用下能够靠近或远离转鼓,其轴线与转鼓轴线平行。试验时,液压缸沿转鼓与车轮中心连线方向且垂直于转鼓表面加载,使轮胎在摩擦力作用下紧密贴合在转鼓上,并随之旋转。标准要求车轮在试验载荷下经过一定次数的疲劳循环后,不得出现可见裂纹和明显塑性变形等破坏现象,且能继续承受载荷。

图2 径向疲劳试验示意图Fig.2 Schematic diagram of radial fatigue test
2 车轮疲劳仿真
车轮弯曲/径向疲劳仿真的一般流程如图3所示。车轮弯曲和径向疲劳仿真,是指完成车轮结构设计后,利用UG、Creo等CAD软件建立车轮的三维模型,通过有限元分析方法进行物理试验的仿真。具体地说是在Ansys Workbench等有限元软件中输入材料属性、划分网格、定义载荷和加载边界条件后,输出应力、应变等结果;对应力应变等的结果进行车轮寿命、安全系数等方面的分析,判断车轮的设计是否合理;对尚需优化的设计及时提出改进建议,从而提高设计效率。疲劳试验是一个动态过程,涉及很多非线性接触,仿真分析的难点在于如何施加载荷和设定边界条件。
3 仿真分析
3.1 三维建模和材料定义
本次仿真分析以规格为16×7 J、材质为A356的铝合金车轮为例。根据设计参数,使用Creo软件建立车轮的三维模型,为保证与物理试验相一致,气孔、倒角等细节与图纸相同。在Workbench中建立材料A356,材料属性:屈服强度为230 MPa、抗拉强度为270 MPa、弹性模量为71 GPa、泊松比为0.33[4],利用Workbench自带的网格划分模块对模型进行网格划分。导入Workbench软件的模型如图4所示。

图3 弯曲/径向疲劳试验仿真流程Fig.3 Simulation process of bending/radial fatigue test
3.2 疲劳试验的模拟
3.2.1 弯曲试验仿真
在车轮的物理试验中,主要承受连接加载轴和车轮的螺栓预紧力、转动产生的离心力和加载轴末端的试验弯矩。忽略车轮旋转过程中产生的离心力影响,预紧力F0和弯矩M可分别按公式(1)、(2)确定[2,5]。
F0=T/(K·D)
(1)
式中:T为螺栓拧紧力矩,Nm;K为拧紧力系数,取0.28;D为螺栓直径,m。
M=(μ·R+d)·Fv·S
(2)
式中:μ为摩擦系数,取0.7;R为轮胎静负荷半径,m;d为车轮的偏距,m;Fv为车轮最大额定载荷,N;S为强化试验系数,取1.6。
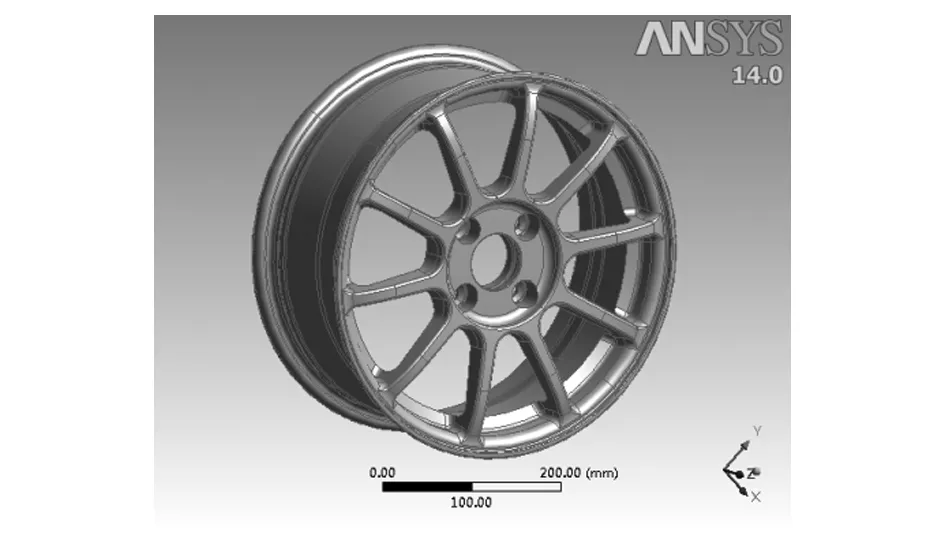
图4 车轮三维模型Fig.4 Three-dimensional model of wheel
在Workbench中,对车轮内侧轮缘处施加无摩擦约束将车轮固定,螺栓与车轮连接孔、车轮安装处与加载轴端面之间设置为接触连接,根据公式(1)求得螺栓预紧力F0为38 265 N,根据公式(2)求得弯矩M为1 824 Nm,因加载轴长L为0.8 m,根据M=FL求得加载轴末端的垂直加载力F为2 280 N。为了模拟车轮在转动过程中的受力情况,采取将车轮固定、弯矩绕车轮旋转的形式,在弯矩转动一周范围内,每10°设置一个求解步,共36个求解步。将预紧力F0和加载力F作为每一载荷步的载荷,分别求解弯矩和拧紧力矩的作用,并用静态分析方法来模拟车轮的动态性能,如图5所示。图5中F为加载力F;E为无摩擦约束;A、B、C、D是4个螺栓的预紧力,且都等于F0。

图5 载荷和边界条件加载Fig.5 Load and boundary condition loading
3.2.2 径向试验仿真

图6 径向载荷分布 Fig.6 Radial loading distribution
物理试验中,车轮主要承受来自轮胎的作用力和充气压力,而旋转离心力的影响较小,可不予考虑[6]。由于轮胎是由橡胶层、钢丝层和帘布层等组成的,其结构较为复杂,且轮胎与车轮的胎圈座处、轮胎胎面与转鼓的接触面均为非线性接触,为简化有限元模型,这里采用J.Stearns等的研究成果[3]。研究表明,轮胎与车轮胎圈座处的接触应力近似服从余弦函数分布,如图6所示。如将接触应力等效视为在车轮40°中心角范围内轮辋内外侧胎圈座上施加的余弦分布力,其径向分布力Wr、最大径向分布力W0分别如公式(3)、(4)所示。
(3)
式中:W0为最大径向分布力,Pa;θ、θ0分别为加载的偏转角及加载的最大偏转角,(°)。
(4)
式中:Fr为径向负荷,N;b、rb分别为胎圈座承载处的宽度与半径,m。
根据国标GB/T 5334—2005中的规定,径向疲劳试验的径向负荷Fr的公式如下:
Fr=Fv·K
(5)
式中:Fr为车轮最大负载,N;K为强化试验系数,这里取2.25。
在Workbench中,对车轮的中心孔、螺栓孔和车轮安装面施加无摩擦约束。为了有效模拟动态径向试验,同样采取将车轮固定、外载荷绕车轮旋转的方式,模拟车轮在转动过程中的受力情况。在车轮转动一周内,每10°设置一个求解步,共设置36个求解步,分别求解每次加载的余弦载荷,并以此来模拟车轮的转动过程,如图7所示。

图7 模拟加载示意图 Fig.7 Diagram of simulated loading
为便于加载,可利用软件的印记面功能,将车轮内、外侧胎圈座的两个承载面平均分成36份。每一载荷步对应的分布载荷可由公式(3)求出。胎压取0.45 MPa,加载在整个轮辋上,如图8所示。

图8 载荷和边界条件加载Fig.8 Load and boundary condition loading
3.3 结果分析
3.3.1 应力分析
车轮的轮辋、辐条和螺栓孔等部分在试验中处于复杂的应力状态,以Von-Mises应力状态作为分析求解的判断标准,最终通过分析得到的弯曲试验仿真和径向试验仿真结果分别如图9、图10所示。

图9 弯曲试验应力图 Fig.9 Stress diagram of bending test

图10 径向试验应力图Fig.10 Stress diagram of radial test
在弯曲试验仿真中,车轮应力集中出现在螺栓孔周围,其最大值为108.97 MPa,发生在与气门嘴相对的螺栓孔内侧面与车轮安装面相交处。分析原因,可能是因为PCD(车轮螺栓孔的节圆直径)尺寸较小,导致与车轮安装中心孔背面之间的壁厚较薄。在径向试验仿真中,车轮应力集中出现在辐条和轮辋处,最大值为77.89 MPa,发生在气门嘴旁的一根辐条与在轮辋内侧面连接根部。究其原因,可能是因为辐条的根部过度圆角较小。另外,从图10中还可以看出,胎压对径向试验的影响还是很大的。
总体上看,车轮仿真结果与其物理疲劳试验相一致,说明此有限元仿真分析有效。
3.3.2 疲劳分析
弯曲/径向疲劳破坏许用应力是在规定的循环次数下,由材料的S-N曲线计算得出。本次有限元仿真中,根据GB/T 5334—2005的要求,弯曲疲劳试验最低循环次数为1×105,径向疲劳试验最低循环次数为5×105,材料的S-N曲线由车轮生产厂家提供。
车轮在弯矩作用下的安全系数与疲劳寿命分别如图11、图12所示。由图11可知,车轮弯曲试验安全系数分布情况与应力分布情况相对应,螺栓孔附近的安全系数较低,最小值为1.65,其余部分安全系数高。安全系数大于1,表明该车轮结构是安全的。图12中的车轮疲劳寿命最低循环次数达到5.98×106,高于标准1×105次的要求。
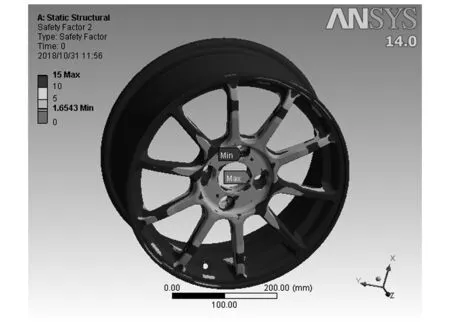
图11 弯曲试验安全系数 Fig.11 Bending test safety factor
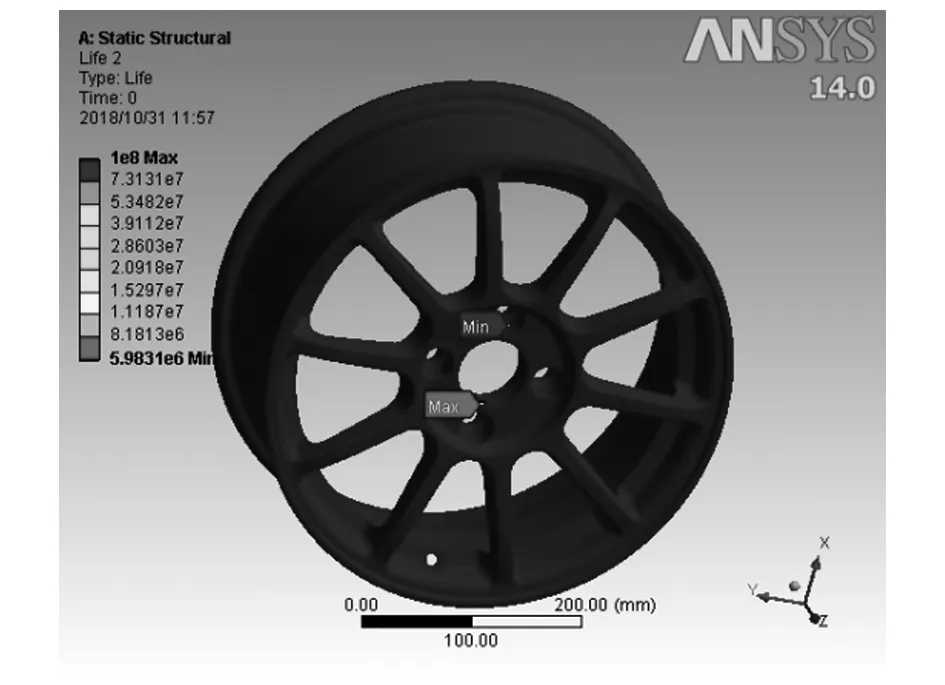
图12 弯曲试验疲劳寿命Fig.12 Bending test fatigue life
车轮径向载荷作用下的安全系数与疲劳寿命分别如图13、图14所示。由图13可知,径向载荷作用下车轮安全系数最小值为2.03,该最低值出现的位置和应力分析中最大值出现的位置相一致,都在气门嘴旁的辐条上。安全系数大于1,表明该车轮结构是安全的。图14中的疲劳寿命最低循环次数达到7.17×106,同样高于标准5×105次的要求。
结合应力分析和疲劳分析的结果,可以看出本次仿真中采用的车轮,无论是最大应力、安全系数还是疲劳寿命,都符合国家标准中车轮安全的要求,并且具有足够的冗余度。因此,在满足疲劳强度的要求下,对车轮结构还有进一步的优化空间,从而降低车轮的质量。

图13 径向试验安全系数Fig.13 Radial test safety factor

图14 径向试验疲劳寿命Fig.14 Radial test fatigue life
4 结论
基于车轮的弯曲和径向疲劳试验的要求,本文使用Creo和Ansys Workbench软件对16×7 J的车轮建立三维和有限元模型并进行仿真分析,给出了仿真流程和仿真思路;采取静态分析模拟动态分析的方式,得到应力和疲劳分析的结果。两种试验仿真中最大应力出现的位置与物理试验的位置相一致,验证了有限元方法预估车轮寿命的有效性,从而可以根据分析结果对车轮进行优化设计。由于轮胎结构的复杂性,在车轮径向试验仿真中,将轮胎传递的载荷近似加载在车轮表面,与实际情况存在一定的误差,需要后续的继续研究;另外,基于S-N曲线的疲劳分析,需要针对不同的材料,应当详细测得交变应力与循环周次之间的对应关系,才能提高疲劳分析的精度。
