基于GA-BP模型的露天矿边坡稳定性预测

臧焜岩，李梅红

(天津工业职业学院，天津 300400)

0 引 言

随着矿山开采的不断深入，开采环境逐渐恶化，越来越多的陡峭边坡形成，矿山边坡灾害发生的频次也有逐年上升的趋势。据统计数据显示，我国每年发生的山体滑坡造成近200亿元经济损失，在影响企业正常的生产经营活动的同时，对生态环境以及人民的生命财产安全也造成了严重的威胁。推动边坡防治和治理技术发展，为矿山安全生产创造良好的环境，有必要开展矿山边坡稳定性预测研究[1]。我国针对露天矿边坡稳定性的研究始于20世纪60年代，随后研究不断发展，边坡稳定性研究总结起来主要包括极限平衡和数值分析两大类，在应用于露天矿研究时，极限平衡分析不能考虑露天矿系统的随机、模糊、可变的动态变化，因此数值分析在研究露天矿稳定性预测时应用更加广泛。随着计算机科学技术的不断发展，人工智能和机器学习算法等广泛应用于露天边坡稳定性预测研究[2]。白润才等[3]在进行露天矿边坡稳定性预测时采用了BP神经网络方法，同时指出了BP神经网络具有容易陷入局部最优问题的不足；付士根[4]在进行露天矿边坡稳定性预测时使用了模糊分析理论，利用点估计法分析了露天矿边坡稳定的可靠性；王旭春等[5]采用极限平衡方法研究了岩体黏聚力、内摩擦角和容重参数等影响因素对边坡稳定性的影响，总结了边坡稳定性规律。刘文生等[6]利用灰色系统模型研究了露天矿边坡沉降变形规律，但是灰色理论对数据满足建模要求程度不高的数据精确度相对较低；周衡等[7]选取了相应遗传参数，利用基因表达式预测了边坡安全系数；姚玮等[8]针对离子型稀土原地浸矿边坡采用随机森林模型进行了稳定性预测；李秀珍等[9]建立了基于支持向量机的露天矿边坡形变位移模型，对模型参数的敏感性没有进一步研究。以上研究多是采用单一预测方法进行研究，存在一定局限性，多种方法进行耦合预测成为研究的发展趋势[10]，并取得了良好的效果，如冯东梅等[11]结合了免疫遗传算法和最小二乘法支持向量机建立了边坡稳定性预测模型，利用因子分析构建了指标体系进行边坡稳定性预测；李云等[12]采用极限平衡计算分析结合有限元分析的方法开展了边坡稳定性预测研究。本文利用遗传算法优化BP神经网络节点的权值和阈值，构建了露天矿边坡稳定性预测模型，通过实例应用表明将遗传算法与BP神经网络相结合可以提高预测精度和学习效率，为准确预测露天矿边坡稳定性提供一种新的方法。

1 GA-BP神经网络原理

作为典型的多层前馈神经网络，BP神经网络向前传递信号，向后反向传递误差。信号在向前传递过程中逐层处理，每一层的神经元信息仅对下一层的神经元信息影响，当输出层的输出不满足期望值时，误差向反向传播，通过不断调整网络结构中的权值和阈值，降低误差，使输出不断逼近期望值。与常规回归算法相比，BP神经网络在非线性映射、泛化和容错等方面具有一定的优势，但是也存在网络结构不确定、局部收敛以及初始权值和阈值非最优等缺陷，由于这些缺陷都会对预测效果产生影响，使得BP神经网络的应用受到很大程度的限制。遗传算法不采用传统的梯度下降法，仅采用适应度函数就可以寻求全局最优解，不受函数连续性和可微性限制，采用遗传算法对BP神经网络初始权值和阈值进行优化能够有效弥补缺陷，克服BP神经网络的弊端。在利用GA-BP(遗传算法优化BP神经网络)模型进行建模预测时主要分为三步：①确定BP神经网络的结构，根据研究的问题确定输入和输出参数的个数，确定遗传算法染色体的个数；②利用遗传算法优化权值和阈值，种群中单个个体包含BP神经网络的权值和阈值，计算每个个体的适应度值，随后进行选择、交叉和变异操作优化确定最优个体[13]；③模型预测，根据步骤②确定的初始权值和阈值赋值，计算得到输出预测函数，利用该网络结构对需要预测的样本输出值进行预测。

2 露天矿边坡稳定性预测GA-BP模型

2.1 输入输出变量的确定

作为一个不断变化的开放体系，露天矿边坡的稳定性受到多种因素的影响，综合起来主要包括边坡几何形态、岩土力学参数以及岩土体中水的作用等几个方面[14]。在边坡几何形态，可以用坡的高度和边坡的坡角来表征；在边坡岩土力学方面，可以用重度、黏聚力、内摩擦角等参数来表征；在岩土体中水的作用方面，可以用孔隙压力比来表征注液量变化和降雨过程。通过搜集大量的历史资料发现，边坡的稳定性与边坡的重度、黏聚力以及内摩擦角成正比。为了便于模型的训练，选取相对较容易获得的参数作为模型的输入和输出变量，其中，重度、内摩擦角、黏聚力、坡度、边坡高度和孔隙比压力6个参数作为边坡稳定性的输入参数，稳定性系数用来表征边坡稳定性作为输出参数。

2.2 预测模型建立

根据确定的输入输出变量可知，神经网络模型的输入节点数为6，输出节点数为1，隐含层节点数的确定采用的计算方法见式(1)。

(1)

式中：h为所要求的节点个数；m代表输入节点的个数；a为调节系数，一般在1～10之间。在反复学习和训练的基础上确定了隐含层数为8，建立的模型结构如图1所示。

与传统的BP神经网络不同，GA-BP神经网络模型采用遗传算法对初始权值和阈值进行优化，优化的过程包括种群初始化、适应度函数的确定以及利用选择、交叉和变异操作求取最优值。染色体长度为(n×h+m×h)+(n+m)，式中第一部分表示权值部分染色体长度，第二部分表示阈值部分染色体长度。适应度函数见式(2)。

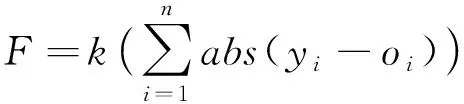
(2)

式中：n为输出的节点个数；yi为第i个样本的实际输出；oi为第i个样本的预测输出；k为系数。最后得到最优个体，对网络初始权值和阈值赋值，网络经训练后输出预测函数。在进行选择操作时采用轮盘赌法，进行实数交叉法，当满足迭代次数结束计算过程。露天矿边坡稳定性GA-BP预测模型的计算流程如图2所示。

图1 BP神经网络拓扑结构Fig.1 Topological structure of BP neural network

图2 矿边坡稳定性预测GA-BP模型计算流程Fig.2 GA-BP modelmomputing flow for prediction of mine slope stability

3 实证分析

3.1 学习样本的选取

选取国内外部分露天矿中已有的稳定边坡和失稳边坡实例共50个样本，随机选取其中的40个作为训练样本，其余10个作为训练样本，其中，安全系数大于1.2表示边坡处于稳定状态，小于1.2表示处于失稳状态。选取的训练样本数据见表1。

3.2 模型预测

反复训练后发现，在经过100次训练后，矿边坡稳定性预测模型呈现出较好的收敛性。由图3可知，该模型的适应度函数为0.5678；由图4可知，最小均方误差值为6.211×10-6，表明该计算模型具有较好的精度。

3.3 模型预测结果分析

根据前文建立的露天矿边坡稳定性预测GA-BP模型，对选取的10个测试样本集的安全系数进行预测，预测结果见表2。从表2预测结果可知，所有预测结果误差均小于6%，平均相对误差为25%，均方误差为3.5%，表明具有相当高的预测精度。

为了进一步分析GA-BP模型的预测效果，开展了与传统BP神经网络用于露天矿边坡预测性能的对比研究(表3)。结果表明，传统BP神经网络预测模型较GA-BP模型而言绝对误差、均方误差大，基于GA-BP模型更适用于露天矿边坡稳定性预测。其原因是GA优化了BP神经网络的初始权值、阈值，从而增强BP神经网络的鲁棒性。

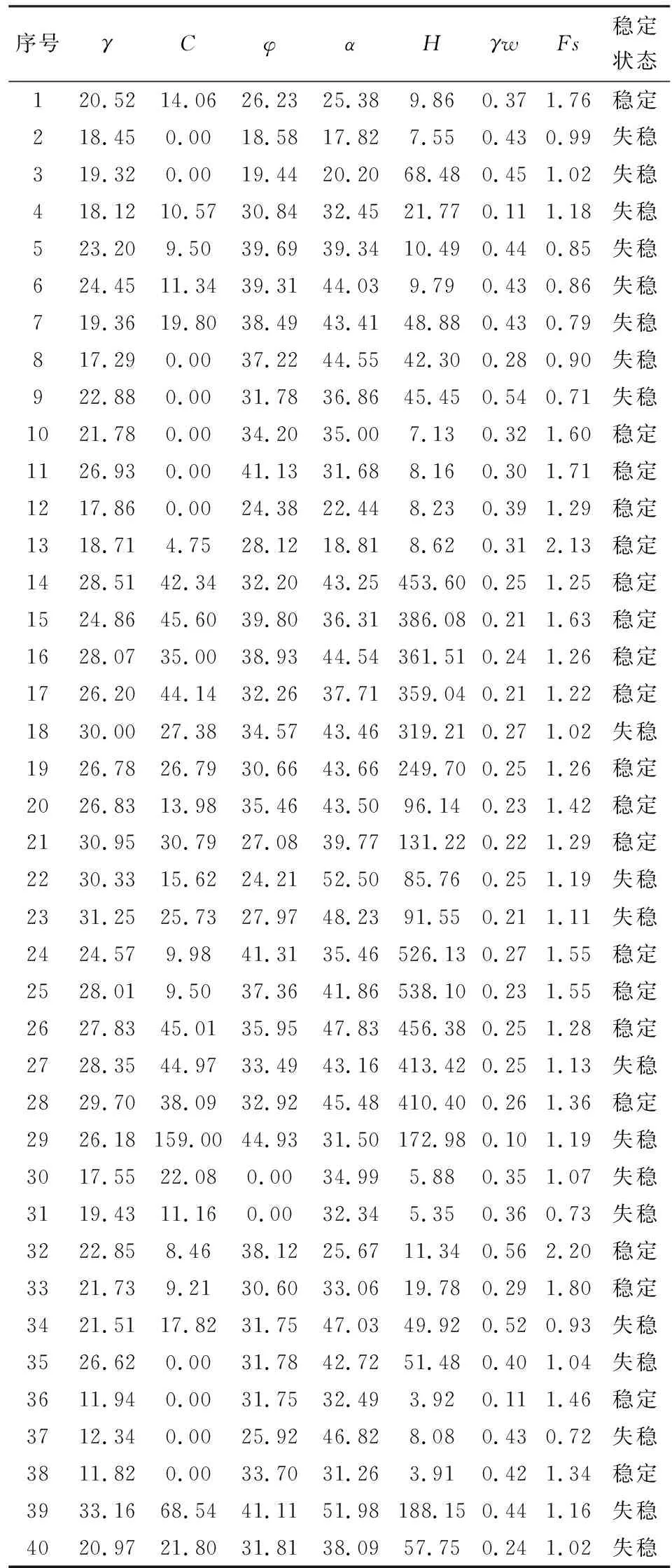
表1 边坡实例训练样本数据Table 1 Sample data of slope case training

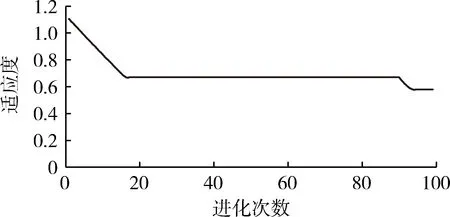
图3 适应度变化曲线Fig.3 The curves of fitness

图4 均方误差变化曲线Fig.4 Mean-square error changing curve

表2 预测模型测试结果Table 2 Predictive model test result

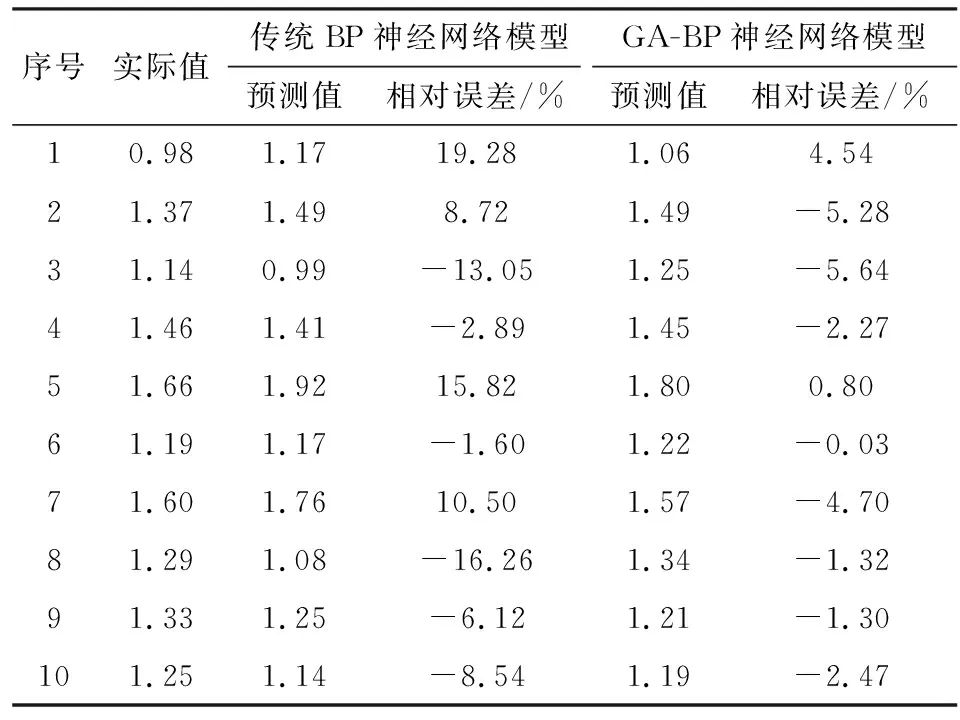
序号实际值传统BP神经网络模型GA-BP神经网络模型预测值相对误差/%预测值相对误差/%10.981.1719.281.064.5421.371.498.721.49-5.2831.140.99-13.051.25-5.6441.461.41-2.891.45-2.2751.661.9215.821.800.8061.191.17-1.601.22-0.0371.601.7610.501.57-4.7081.291.08-16.261.34-1.3291.331.25-6.121.21-1.30101.251.14-8.541.19-2.47

表3 预测结果比较Table 3 Comparison of predicted results

4 结 论

1) 本文结合遗传算法和BP神经网络建立露天矿边坡稳定性预测模型，克服了传统BP神经网络不稳定性和收敛速度慢的问题，平均相对误差和均方误差相对较低，预测精度高，为解决复杂影响因素下的露天矿边坡稳定性预测问题提供了一种新的有效办法。

2) 露天矿边坡稳定性预测GA-BP模型考虑了重度、内摩擦角、黏聚力、坡度、边坡高度和孔隙比压力等主要影响因素，所采用数据容易得到，具有很好的适用性和可靠性。