对初中长度测量中累积放大法有效数字的思考*

黄 鹏

(重庆巴蜀常春藤学校 重庆 401127)

长度测量是学生学习物理的第一次实验操作，其中累积放大法作为长度测量的特殊方法，教师一般都会给学生介绍．但是,在教学中笔者发现,对于累积放大法所得结果的有效数字位数在教师中存有争议．本文试图从测量不确定度的角度去理解累积放大法的有效数字，同时笔者发现这样也能解释高考中让教师费解的电表读数问题，可见该方法具有一定的推广价值．

1 问题的引入

【例1】(2013年河南省沁阳市和焦作市一模)将粗细均匀的金属丝在笔杆上密绕30圈，如图1所示，线圈总长度是______cm，金属丝直径是______mm.

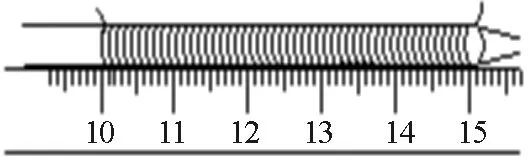
图1 例1题图

参考答案：5.00，1.7．

分析：第一空的答案大家没有异议．对于第二空，计算直径的式子为

大部分教师认可金属丝直径为1.7mm，他们认为最后结果只能准确到刻度尺的精确度1mm；少数教师认为金属丝直径应为1.67mm，因为总长度的测量是正确的，直径的数学计算也是正确的，有效数字位数应该与总长度有效数字位数一致．到底哪一种考量更加合理呢？

2 测量不确定度

2.1 不确定度的定义

测量不确定度和测量误差之间既有区别又有联系．测量误差是指测量值与真实值之间的差异．由于真实值一般不可知，因此,测量误差也不可能准确知道．由于测量误差的存在而对被测量值不能肯定的程度称为不确定度[1]．测量不确定度是用来表征被测量的真值所处量值范围的评定，是用于表征合理赋予的被测量值的分散性参数．

2.2 不确定度的分量

由于误差来源很多，测量结果的不确定度一般包含若干分量．一般我们把误差归为A,B两类不确定度分量，然后合成得出合成不确定度．A类分量是指重复测量后采用统计方法计算的不确定度，通常认为它服从正态分布规律，因此可以像计算标准偏差那样用“贝塞尔公式”计算

B类分量是指用非统计方法估算的不确定度分量，在大学物理实验中一般只考虑计量器具误差这一主要因素，用仪器的示值误差(限)ΔINS来表示测量的B类不确定度分量ΔB≈ΔINS[2]．

仪器的示值误差(限)表示在正确使用仪器的条件下，仪器示值与被测量真值之间可能产生的最大误差的绝对值，通常由制造工厂或计量部门使用更精密的仪器、量具，经过检定比较给出，一般写在仪器的标牌上或说明书中[2]．物理实验常用仪器具的示值误差(限)如表1所示.

表1 实验常用仪器具的示值误差(限)

2.3 合成不确定度

2.4 不确定度的有效数字

按照国际通用的《测量不确定度表示指南》(GUM)和国家质量技术监督局发布的《测量不确定度评定与表示》(JJF1059.1-2012)的规定，在测量结果的最终表述中，不确定度的数值最多为两位有效数字，测量结果的取位应该与测量不确定度的末位对齐[3]．对于何时取一位、何时取两位，大学物理实验教材和相关文献中通常是这样规定的：首位数字为1和2时，测量结果不确定度的有效数字可以取两位，当不确定度首位数字是3或3以上时，可以保留一位有效数字[1,2,4]．因此,有时需要对测量结果的不确定度进行修约，《测量不确定度评定与表示》(JJF1059.1-2012)给出了两种修约方法，一般采用的是“四舍六入，五凑偶”；其二是“宁大勿小”的原则，即只要测量结果不确定度的末位后还有数值就一律进上去，不管这个数多大．

3 应用不确定度判定有效数字位数

3.1 累积放大法中的应用

初中长度测量中的累积放大法是由于被测物太小和测量仪器精度太低，无法直接测出被测物的长度，而将被测物累积放大进行测量的方法．它要求累积的被测物必须相同，累积过程中的操作方法也必须正确，避免引入新的误差．比如，用刻度尺测量金属丝直径时，金属丝的粗细必须均匀，也必须紧密排列．

3.2 高中电表读数中的应用

【例2】(2014年高考理综全国Ⅰ卷23题第2问)实验得到的部分数据如表2所示，其中电阻R=3.0Ω时电流表的示数如图2所示，读出数据，完成下表．答：①______，②______．

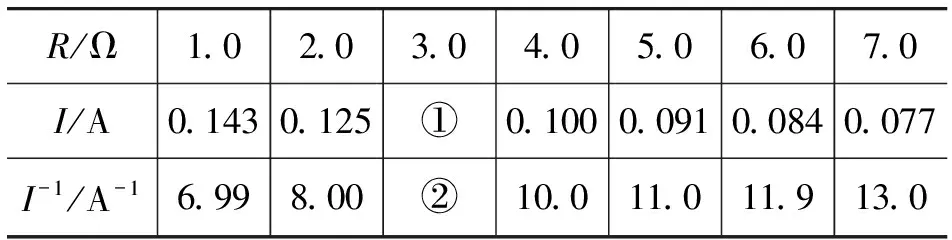
表2 部分实验数据表

参考答案：0.110，9.09．

图2 例2题图

分析:中学阶段电表一般为2.5级，则该电流表的读数不确定度为Δ≈ΔINS=200mA×2.5%=5mA，因此，读数结果应该与安培的千分位对齐，记为0.110A是合理的．关于电表读数问题的更多例子，可参阅文献[5,6]，此处不再赘述．

4 建议

《义务教育物理课程标准(2011年版)》要求学生会使用简单仪器进行实验，会正确记录实验数据．刻度尺的读数是中考的考察重点．对长度测量中累积放大法有效数字的位数，有教师要求学生“计算结果与原刻度尺精确度必须一致”，也有教师从数学的角度要求“计算结果与总长度有效数字位数一致”，正是这两种不同的要求导致了解答例1时的争议，因此，笔者建议告诉学生累积放大法将测量误差进行了平均，相当于提高了刻度尺的精确度，可以将计算结果保留到精确度提高后的下一位，这样既能够让结果更具科学性，也在学生理解的能力范围之内．以此与同仁们商榷，希望能够与同仁们达成共识，避免类似争议．

虽然中学阶段不要求学生掌握仪器的示值误差(限)ΔINS，也不要求作测量误差估计，更不要求计算测量不确定度；但是，作为教师应该清楚科学的测量结果如何表示，这样教师才能引导学生用更科学的方式表示测量结果，才能在教学中做到深入浅出、厚积薄发．