Matlab GUI在大学物理实验中的应用

王潇曼

(深圳市光明区爱华小学 广东 深圳 518107)

谢翠婷 丁格曼

(华南师范大学物理与电信工程学院 广东 广州 510006)

在高校物理实验领域，信息技术和实验有机结合形成的虚拟仿真实验室已成为物理实验创新的热门研究课题.测量共轴通电线圈轴线上的磁感应强度是比较典型的基础物理实验研究，但因课时、器材等限制，难以在基本实验的基础上进行拓展和深入探究.而霍尔效应实验中变温情况下的实验数据量大，传统使用Excel处理的过程较为繁琐.

Matlab强大的数据处理、可视化功能及人机交互式界面设计，能在一定程度上克服物理实验实践的限制，起到相辅相成的作用.本文将展示利用Matlab GUI仿真模拟共轴通电线圈实验，制作可反复操作的霍尔效应实验数据处理界面的实例，体现Matlab GUI在促进物理实验教学及学习方面的有效性和便利性.

1 共轴通电线圈实验的仿真演示

作为典型的基础物理实验，共轴通电线圈实验有助于学生学习和掌握弱磁场的测量方法[1].

如图1所示，共轴通电线圈是由两个半径为R的共轴圆形线圈组成，相距为2L，通有同向电流I.以两线圈轴线的中点为原点O，建立坐标系，P为轴线上一点.

两线圈对P点的磁感应强度分别为[2]

(1)

(2)

其中

则合成的磁感应强度大小为

B=B1+B2

(3)

方向沿z轴方向.

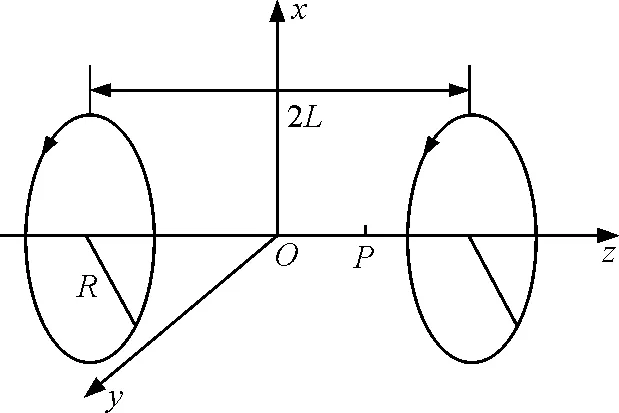
图1 共轴通电线圈实验示意图

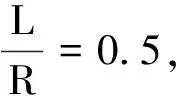
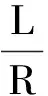
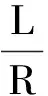
图2是仿真得到的共轴通电线圈轴线上磁感应强度合成曲线图.

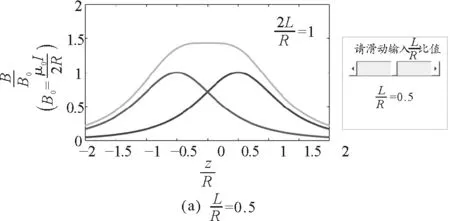
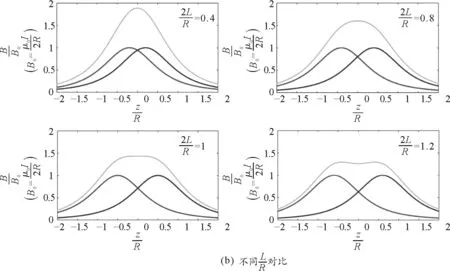
图2 共轴通电线圈轴线上磁感应强度合成曲线图

实验室一般只测量共轴通电线圈轴线上的磁感应强度，而轴平面上的磁感应强度的变化却未有探究.利用Matlab GUI也可方便地仿真演示出共轴通电线圈轴平面上的磁感应强度.

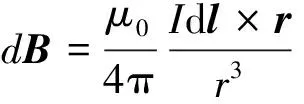
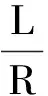
slider的callback程序中主要添加了以下代码[3].

Nx=101;Nz=101;R=1;%设定观测点网格数，环半径

val=get(handles.slider1,′value′); %获取控件slider1的数值

L=val;sval=num2str(val);

set(handles.text2,′String′,sval); %将获取的数值在控件text2中显示

axes(handles.axes1);

x=linspace(-R,R,Nx);z=linspace(-2,2,Nz); %设定观测点范围及数组

Nh=100;T0=linspace(0,2*pi,Nh+1); %环电流及环的圆周角分段

T1=T0(1∶Nh);

yb=R*sin(T1);xb=R*cos(T1); %设置环各段向量的起点坐标yb，xb

T2=T0(2∶Nh+1);

ye=R*sin(T2);xe=R*cos(T2); %设置环各段向量的終点坐标ye，xe

dlz=0;dly=ye-yb;dlx=xe-xb; %计算环各段向量的dl的三个长度向量

z1=-L;z2=L; %左环及右环各段环向量的z坐标

y1=(ye+yb)/2;y2=(ye+yb)/2;

x1=(xe+xb)/2;x2=(xe+xb)/2; %计算环各段向量中点的三个坐标分量

for i=1∶Nx %循环计算各网格点的B(x,z)值

for j=1∶Nz

rx1=x(i)-x1;ry1=0-y1;rz1=z(j)-z1; %观测点在y=0平面上

r13=sqrt(rx1.^2+ry1.^2+rz1.^2).^3;

rx2=x(i)-x2;ry2=0-y2;rz2=z(j)-z2;

r23=sqrt(rx2.^2+ry2.^2+rz2.^2).^3;

dl×r_x1=dly.*rz1-dlz.*ry1; %计算dl×r的x和z的分量

dl×r_z1=dlx.*ry1-dly.*rx1;

dl×r_x2=dly.*rz2-dlz.*ry2;

dl×r_z2=dlx.*ry2-dly.*rx2;

Bz(i,j)=sum(dl×r_z1./r13)+sum(dl×r_z2./r23); %各环产生的磁场分量

相加

Bx(i,j)=sum(dl×r_x1./r13)+sum(dl×r_x2./r23);

end

end

B=sqrt(Bx.^2+Bz.^2)./(2*pi); %计算各环产生的磁感应响度的模

拉动滑动条，实验结果随之变化，如图3所示.

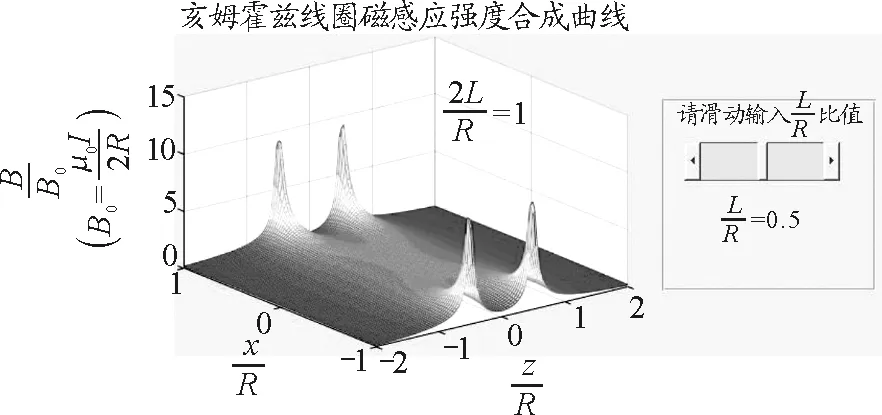
图3 共轴通电线圈轴平面磁感应强度合成曲面图

总之，利用Matlab GUI对共轴通电线圈进行仿真，通过对控件的合理选用，使得实验参数随时可变，能更快捷、直观、实时看到实验结果的变化，方便研究者进行比较研究；同时,从对轴线上的磁感应强度的研究拓展到轴平面，使实验过程更深入全面，加深学生对共轴通电线圈实验的理解，从而提高学生对实验探究的兴趣和积极性.

2 霍尔效应实验数据的优化处理

霍尔效应实验是指对通电的导体或半导体施加一磁场与电流方向互相垂直，则在垂直于电流和磁场方向上出现一横向电势差的现象[1].霍尔效应中，半导体材料的导电机制主要取决于所处的温度.当处于低温时，以杂质电离为主；在高温时，以本征激发为主.因此，半导体的变温曲线分为3个区：高温的本征导电区，低温的杂质电离区和两者之间的饱和电离区.

在高温本征导电区，霍尔系数R与温度T的关系近似为

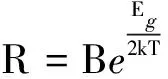
因此禁带宽度Eg为

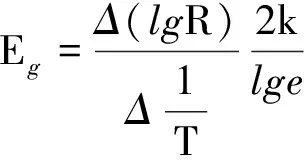
(4)

在低温杂质电离区，有

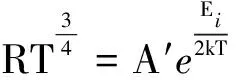
因此杂质电离能Ei为

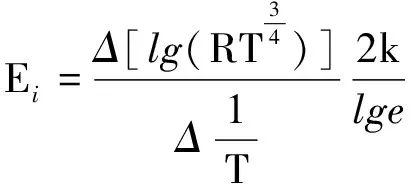
(5)

出自吴先球、熊予莹主编的《近代物理实验教程》的物理实验“霍尔效应”得到的实验数据是100多组温度T对应4个不同的霍尔电压V1,V2,V3,V4，处理数据时需要代入公式

霍尔系数表达式

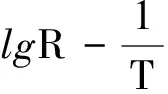
大学物理实验中数据处理环节不可避免.新时代的学生要学会选择合适的辅助工具和手段处理复杂、量多的数据.变温霍尔效应不同温度下对应的不同的霍尔电压，数据可达100多组.传统地用Excel处理这些数据，要多次插入函数，画不同的曲线，过程繁琐复杂.利用Matlab GUI制作一个可多次操作的数据处理界面，能有效提高计算效率.

霍尔效应的数据处理界面布置如图4所示.

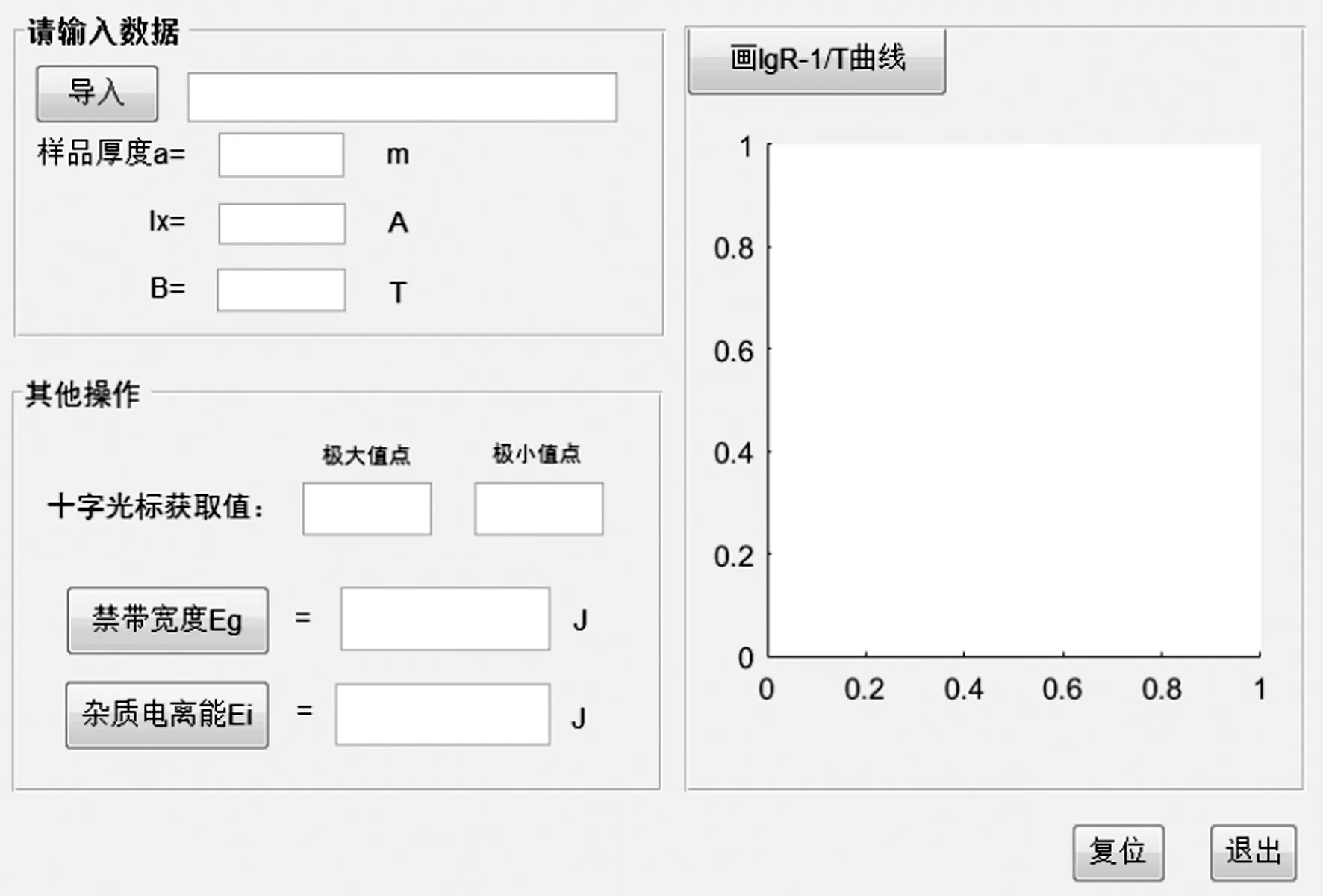
图4 霍尔效应实验数据处理的GUI布局

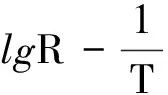
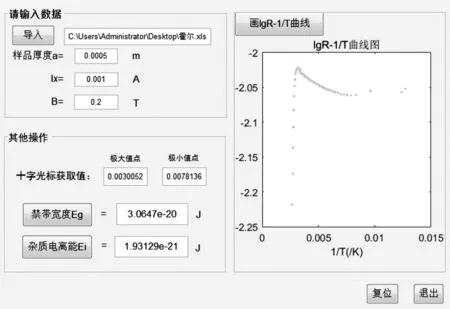
图5 霍尔效应实验数据处理结果

3 结束语

将Matlab GUI与大学物理实验有机结合，充分发挥Matlab GUI强大的计算、图形处理和人机交互功能，可使教学过程更加生动形象，达到事半功倍的效果.另外，它不受实验仪器和场地的限制，能让物理的学习更生动有趣，简洁高效，有助于学生理解实验原理、总结实验规律，提高学生学习物理的兴趣和对实验的探究热情[4，5].