基于斜帐篷映射的混沌加密置乱算法研究

李红梅，徐 凌

(1.安徽新华学院，安徽合肥 230088；2.中国科学技术大学，安徽合肥 230000)

1 混沌理论与斜帐篷映射

斜帐篷映射是一种根据X的范围来确定结果的分段性函数，具体可表示：

(1)

其中，X∈[0,1]是系统的初始条件，μ∈(0,1)是其控制参数。

图1是由Matlab软件得出的斜帐篷映射的分岔图，横轴表示控制参数μ，0<μ<1，纵轴表示X，0≤X≤1。利用C++软件编写程序，对斜帐篷映射得到的随机值的分布情况进行分析，表1是迭代30000次的结果，可以看出各区域中随机值的个数及所占百分比比较平均，斜帐篷映射产生的随机值的分布是比较均匀的。

2 加密方案设计

2.1 加密过程

图像处理中常用的灰度图像由一组像素组成，在处理过程中可以将组成图像的所有像素看成是一个向量组P，其值Pi是图像中像素的集合，Pi=(xi,yi,valuei)，其中，valuei是该像素的灰度值，xi和yi是像素的横坐标和纵坐标。加密过程中主要是先用相关映射函数生成的随机值序列作为参数对原图中像素进行置换，采用位置置换或者比特置换的方案均可。斜帐篷映射产生的混沌序列的分布更平均，因此本文实验中采用该映射函数生成相应的混沌序列对组成图像的像素进行处理，最终生成加密图。

图1 斜帐篷映射分岔图

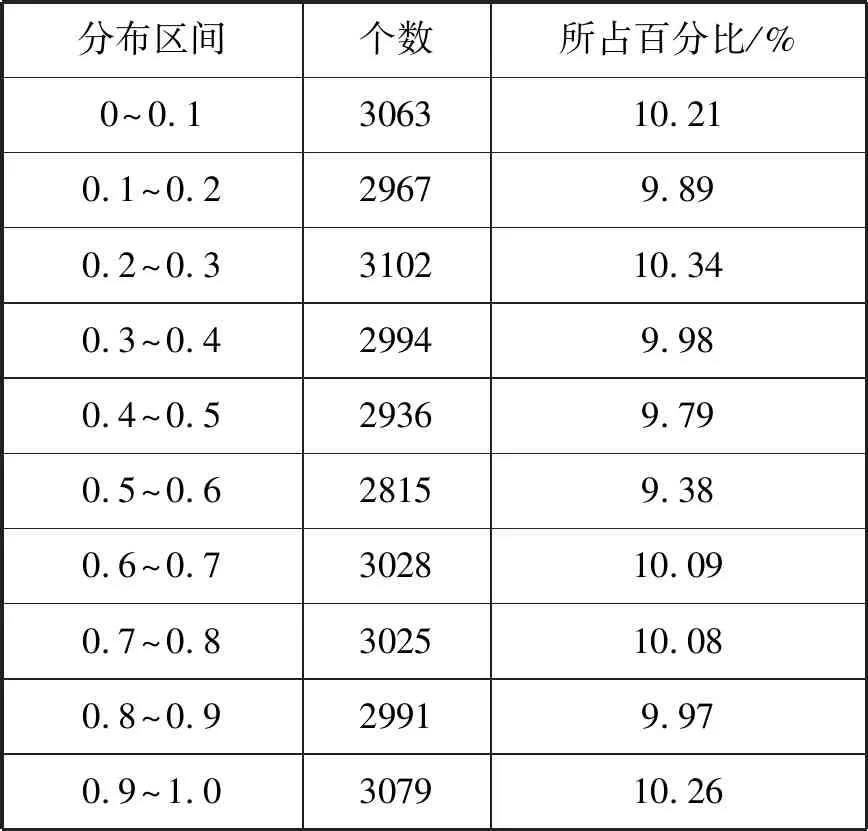
表1 斜帐篷映射随机分布图

在图像信息中，每个像素均由8位二进制数组成，每位二进制数因其所处位置不同会表示不同量的信息，如数1在第1位时表示的是1，而在第8位时则表示128，在i位置所表示像素信息所占的比率P(i)可以通过公式(2)进行计算。

(2)

由表2可知，低4位包含的信息量不到6%，而高4位占有图像总信息的94.125%，可见图像的高位比低位更为重要。因此在采用混沌映射的结果作为系数对图像信息进行置换时，为减少执行时间，可将低4位作为一个整体，而高4位占有的信息量较大，需要将每位进行独立的处理。

表2 不同位置的像素信息百分比

在加密阶段，首先通过斜帐篷映射产生混沌序列，将该结果作为Arnold映射的参数，通过改变原图像中像素元素的位置或数值来对图像进行置乱处理，该映射是混沌置乱系统中比较常用的方法之一，其定义如公式(3)所示，将像素位置(x,y)转换为(x1,y1),p和q为该映射函数的参数。

(3)

位平面置换操作算法的具体设计流程如图2所示，其中，pi和qi是每一轮Arnold映射的参数，其值是通过设置斜帐篷映射初值μ=0.998，xn=0.012345678和xn=0.087865765433212时，再结合公式(4)可计算得到(pi,qi)的值；结合置换过程的次数ni可完成加密过程，本文中将ni设置为1。

(4)

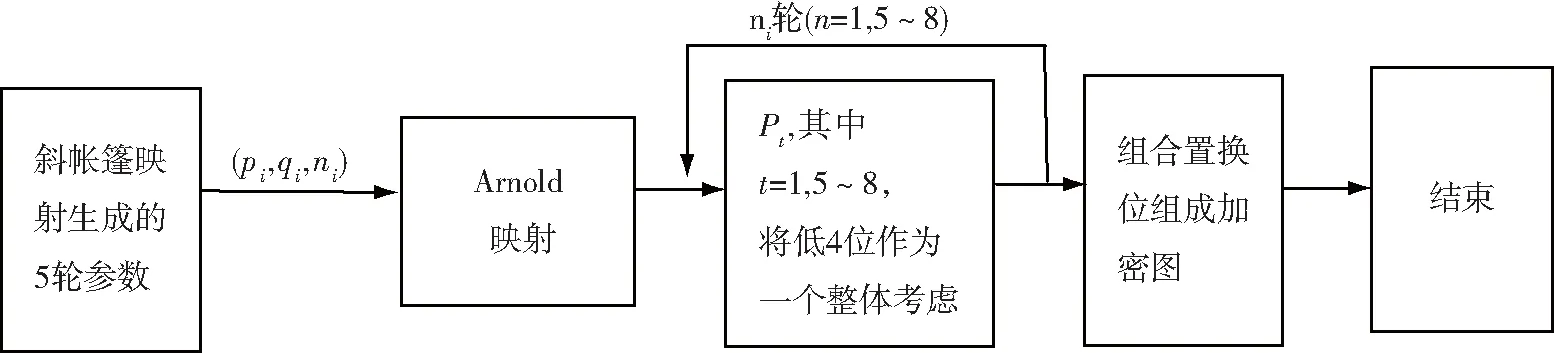
图2 位平面置换操作

2.2 算法结果分析

运行本文算法可得到如图3所示的结论，通过计算可知原图与解密图像素差异数为0，因此该加密方案具有无损加密的特性。

图3 算法结果图

3 加密评估与测试

3.1 信息熵测试

为了描述图像中所包含的信息量大小，C E Shannon提出了信息熵的概念，若图像有n种灰度值mi，i=0,1,2,…,n-1，P(mi)是各个灰度出现的概率，通过公式(5)计算得到信息熵H(m)，其信息熵越大，表示其灰度分布越一致，对于理想的随机图像，其信息熵等于8，加密后的图其信息熵应尽量接近于8。

(5)

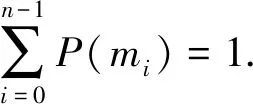
通过计算可知，原图信息熵为7.568279，加密图信息熵为7.997271，其值已经非常接近理想值8。

3.2 直方图分析

从图4可看出，加密图的直方图的分布比较均匀，与原图差别较大。直方图的分布可用方差来衡量，方差可用来表示直方图与其平均值之间的分散程度，其值越小表示其分布越均匀，可通过公式(6)进行计算，原图直方图的方差为5668.834，加密图直方图的方差为167.7309，可见加密图像素的分布与原图相比更加均匀。

(6)

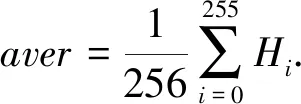
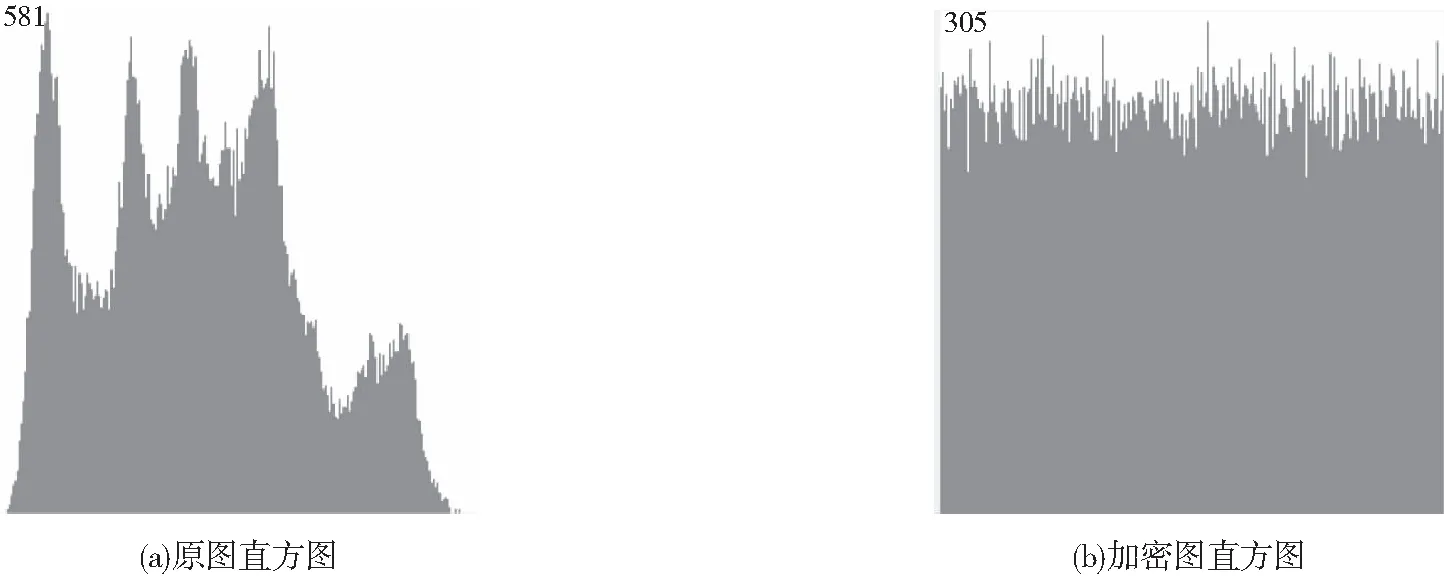
图4 直方图图示

3.3 相邻像素的相关性分析

为讨论像素间的相关性，随机选择垂直、水平和对角三个角度通过图示来进行分析，从图5可以看出加密图中相邻像素间并无明显相关性。

图5 相关性图示

4 结语

综上所述，首先对斜帐篷映射的特性及其所产生的混沌序列进行分析，发现该映射所产生的随机值的分布更加均匀，则Arnold映射使用该斜帐篷映射的结果作为参数来改变图像中像素的值和位置。通过对其加密前后的信息熵、直方图和相邻像素的相关性进行分析可知该算法具有较好的性能，加密效果很理想，具有实际应用价值。