基于高维随机矩阵的异常用电行为识别方法

王鹏，刘长江，刘攸坚，韦景康，邱凌，吴远超，李自怀

(1.广东电网有限责任公司佛山供电局，广东 佛山 528000；2.武汉新电电气股份有限公司，湖北 武汉 430073)

计量装置故障和窃电等异常用电行为会造成电网的非技术性损失[1-2]，给电力企业造成经济损失。传统的用电异常识别主要依靠电力稽查人员定期巡检，强调人工管理[3]，需投入大量的人力、财力和物力，且不能达到预期效果。随着智能电表的普及和电力系统信息化程度的高速发展，电力企业存储了海量的用户侧电量数据[4-5]，通过充分挖掘电力大数据的潜在价值，及时识别用户异常用电行为，减少经济损失，对智能电网的发展有着重要意义[6-8]。

国内外学者在利用电力大数据分析用户异常用电行为识别方面进行了相关研究[9]。文献[10]和[11]利用聚类算法分析每类用户的用电负荷特征，得到特征曲线，以负荷曲线和特征曲线的偏离度判断用户行为是否异常；文献[12]基于密度的聚类技术分析用户行为，给出不同簇的异常程度量化值，进而得到用户异常得分排序；文献[13]以负荷骤降为特征，基于皮尔森相关系数法、贝叶斯网络和决策树检测非技术性损失；文献[14]基于无监督学习方法，通过主成分分析对特征量降维，利用网格处理优化离群算法计算用户离群程度，设定阈值找出异常用户；文献[15]利用用电信息采集平台数据，基于距离的离群点算法建立模型，识别欠压法和欠流法窃电用户；文献[16]利用BP神经网络建立了反窃电模型。另外，还有学者利用时间序列分析[17]、Storm滑动窗口算法[18]和粒子群算法[19]等进行在线监测数据异常方面的研究。上述研究在用户异常用电行为识别方面取得了一定成果，但在算法的精确度、鲁棒性、可靠性及效率等方面还有待改进和提高。

本文基于高维随机矩阵理论建立用户异常用电行为识别模型，首先选取用户相关运行参数建立高维随机矩阵及其协方差矩阵；然后构建协方差矩阵特征值的谱分析函数，利用M-P定律和单环定律分析特征值分布情况，判断用户用电行为是否异常；最后利用平均谱半径变化曲线波动情况定位用户异常用电时间区段，并通过实例分析，验证该方法具有更高的精确度、运算效率和可靠性。

1 高维随机矩阵理论

高维随机矩阵是一个维度为n×p的矩阵，如果它的元素均为随机变量，则称该矩阵是随机矩阵，将n和p趋于无穷、比值趋于常数的随机矩阵称为高维随机矩阵。本节介绍有关高维随机矩阵的基本概念及本文所用的重要定理，作为异常用电行为识别方法的理论依据。

1.1 基本概念

高维样本的经验谱分析是判断数据是否异常的主要方法，即通过分析样本协方差矩阵的经验谱分布函数的性质来判断异常。

令随机矩阵Xn=(xij)m×k，其随机变量xij可以取复值，且相互独立并满足期望为0、方差为1的独立同分布，则样本的协方差矩阵

(1)

(2)

其中x*表示x的共轭转置。对任意p×p且特征根只为实数的矩阵，记其特征根为λ1≤λ2≤…≤λp，定义矩阵的经验谱分布函数

(3)

其中I为示性函数。

一般地，经验谱分布函数的极限称为极限谱分布函数[20]，通常极限谱分布函数是非随机的。

1.2 高维随机矩阵定律

1.2.1 M-P定律

1967年，Marchenko和Pastur首次证明了独立同分布随机矩阵的协方差矩阵的特征值分布，在维数趋于无穷时，渐近收敛到一个特定的函数，这就是M-P定律[21]。M-P定律近似描述了行数与列数不同的随机矩阵奇异值的特征情况，当矩阵Xn=(xij)m×k的所有元素为独立同分布的复随机变量，当m/k=c→Y∈(0,)，Y为常数时，Xn满足M-P定律，即

(4)

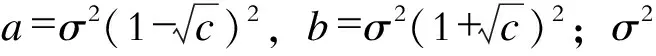
1.2.2 单环定律

假设随机矩阵Xn=(xij)m×k可以分解为可分解为Xn=PTQ，其中P和Q为k阶Haar酉矩阵，T为对角阵，对角线元素是Xn的奇异值。当满足一定条件时，矩阵Xn的极限谱分布由其奇异值的概率测度确定，极限谱分布依概率收敛到函数

(5)

式中：c为Xn的行列比；λz为Xn的任一特征值。当所研究的系统稳定时，Xn的特征值在复平面上分布在一个内环半径为(1-c)k/2、外环半径为1的圆环上。当m,k→，且行列比m/k=c∈(0,1]时，谱分布函数的特征值在复平面上的内径大小由随机矩阵Xn的行数列数确定[22-24]。

2 用户异常用电行为识别方法

高维随机矩阵理论的大数据融合结构灵活多变，矩阵元素可以是确定数据，也可是符合某特定分布的随机数。高维随机矩阵的建立原则是通过调整行和列中的数据得到最优行列比。

电网运行中产生很多用电数据，计量自动化系统可以实时监控并存储各用户的电流、电压、有功功率、无功功率以及功率因数等信息[22]。当系统正常运行时，这些参数以时间序列的形式存储在系统中，且平稳波动；当电网用户存在异常用电行为时，这些参数的数据将出现突变点，波形中出现尖峰。结合高维随机矩阵理论和用电信息采集平台的参数特征，用户异常用电行为识别方法建模步骤如下：

a)根据异常用电用户识别的目的和大数据来源，选取某些节点上某些种类的电网状态变量的量测数据来构建高维随机矩阵，并调整行列比，以达到最合适的比值；

b)求解构建矩阵的协方差矩阵；

c)求解协方差矩阵的特征值，得出特征谱分布及谱密度函数，并根据M-P定律和单环定律等理论分析其分布情况，判别用电情况。

2.1 用户用电行为的高维随机矩阵表示

对于电网中的w条线路或w个量测设备，每一条线路或每个量测设备为一个观测点，则共有w个观测点，每个观测点在t时间区段均可得到用电参数的一个T行1列时间序列向量xi,i=1,2,…,w；则所有观测点采集到的用电参数的时间序列向量构成一个w×T的时间序列矩阵，即

(6)

(7)

当数据采样频率不同，将矩阵所有元素进行标准化处理，目的是去量纲化和数值归一化，使各指标具有可比性。

2.2 基于高维随机矩阵的异常用电用户识别方法

当线路存在异常用电用户时，高维随机矩阵的协方差矩阵特征值分布将会偏离M-P定律，可以通过偏离程度判别异常用户。同时，单环定律的内径和外径大小与异常数据无关，是一个唯一确定的值。当存在异常数据时，随机矩阵的特征值将会有部分落在圆环外侧，可用通过特征值谱分布分析来识别异常用户数据。基于高维随机矩阵的用户异常用电行为识别步骤如图1所示，具体步骤如下：

步骤1，从计量自动化系统采集某台区不同线路某时间区段内各线路的总有功功率或其他各用户的用电数据(包括电压、电流、有功功率、无功功率、功率因数等)；

步骤2，选取该台区不同线路的日用电量构建高维随机矩阵，并求取其复数域的等效矩阵；

步骤3，通过该矩阵的特征谱分布及谱密度函数判断各线路用电情况；

步骤4，判断为异常的线路，进一步选取该线路上各用户的用电数据构建高维随机矩阵，并通过圆环定律及平均谱半径精确定位异常用户和异常时间区段并输出识别结果。

3 实例分析

基于上述提出的高维随机理论建模与异常用户识别方法，本文选取某电网公司某台区的线路进行判别，该台区供电网络拓扑结构如图2所示。该台区有a、b两条分支线路，共12个节点，节点1为电源节点，其余节点均为用户节点。本节将首先对该台区分支线路a、b进行分析，判断各分支线路的用电情况；然后根据判别结果对于存在用电异常的线路进一步选取该线路上的用户进行分析，精确定位异常用户及该用户异常用电的时间区段。

3.1 异常线路确定

从计量自动化系统获取线路a和b于2015年1月至2016年7月的日用电总量数据，构成维度分别为5 810×1和8 715×1的时间序列矩阵。2个矩阵经式(7)变化并归一化处理后变为维度分别为10×581和15×581的高维随机矩阵；2个矩阵的谱分布特性如图3和图4所示。

表1 用户用电行为高维随机矩阵Tab.1 High dimensional random matrix for user’s electricity consumption behavior

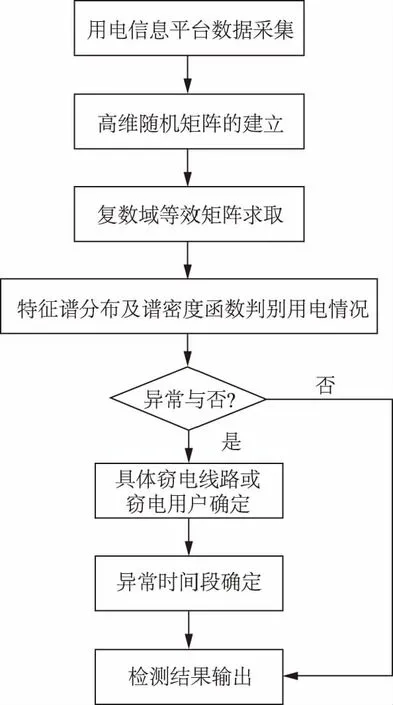
图1 基于高维随机矩阵的用户异常用电行为识别步骤Fig.1 Recognition steps aboutabnormal electricity consumption behavior based on high dimensional random matrix

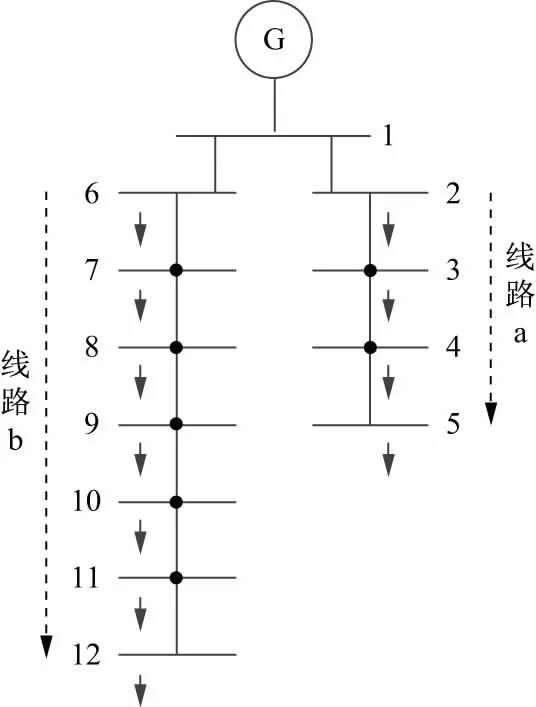
图2 某台区供电网络拓扑结构Fig.2 Power supply network topology of a certain area grid

基于大数据理论，当系统正常运行无异常情况发生时，日用电总量数据矩阵的协方差特征值集中分布于圆环内，且特征值谱半径平均值介于内外环半径之间；当存在异常时，协方差矩阵的特征值集中分布在内圆环心，且特征值谱半径平均值小于内环半径。所以对比图3中的(a)和(b)可知，线路a存在用电异常用户。

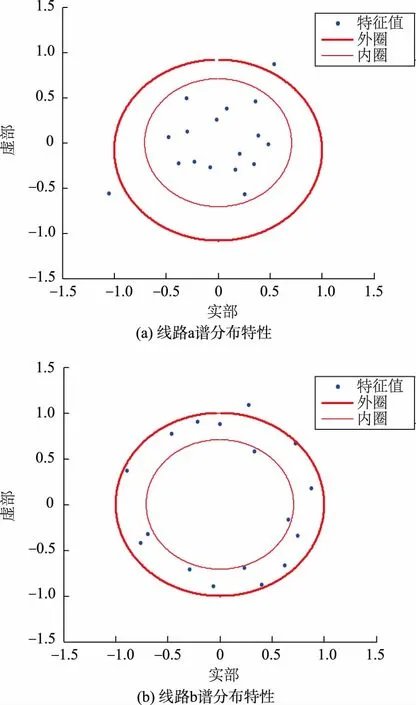
图3 两条线路协方差矩阵特征值谱分布Fig.3 Spectral distribution of eigenvalues of covariance matrix of two lines

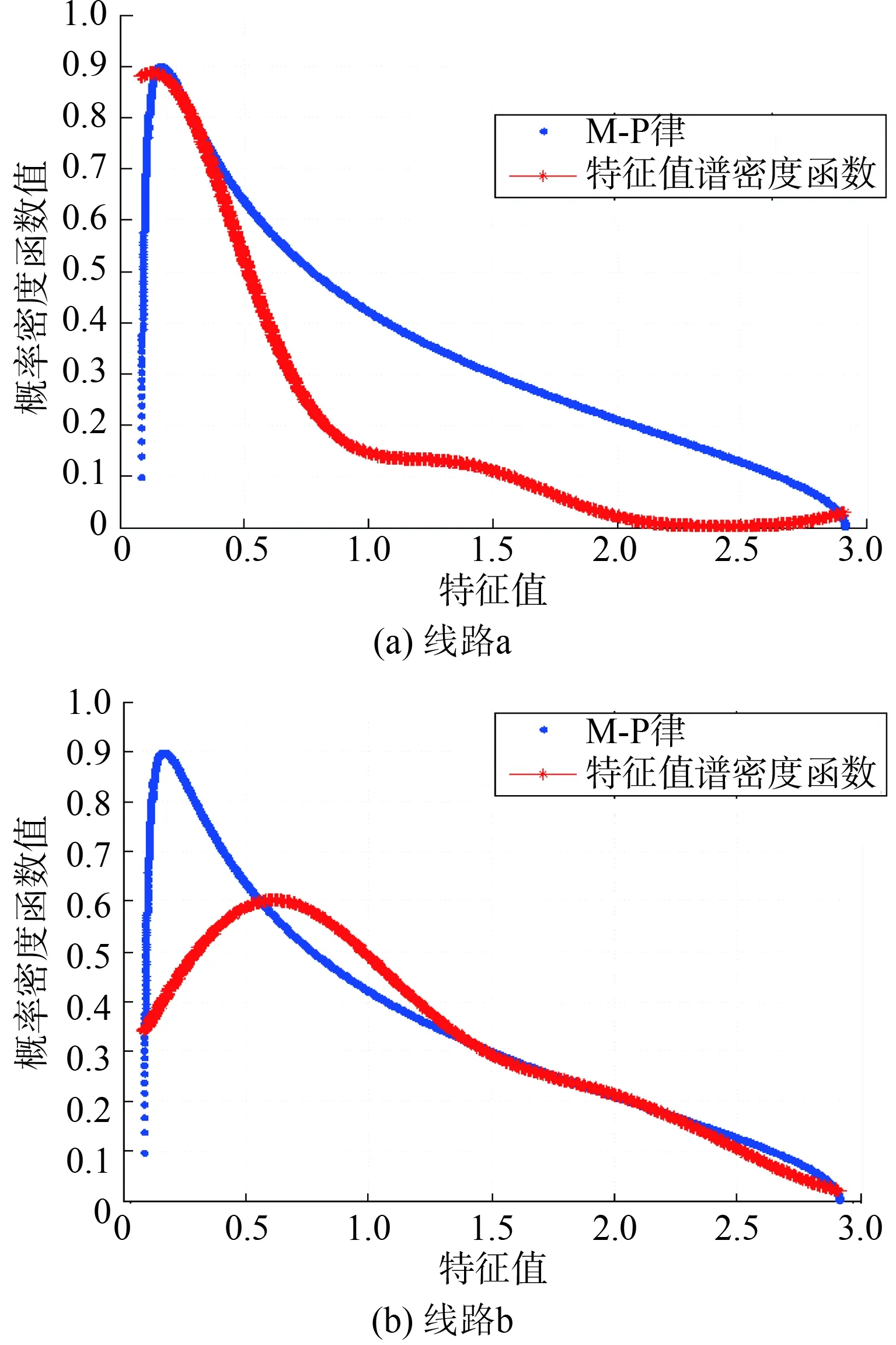
图4 两条线路谱密度函数与M-P律Fig.4 Spectral density functions and M-P’s laws of two lines

基于大数据理论，当系统正常运行无异常发生时，矩阵的特征值谱密度函数遵循M-P定律；当存在异常时，由于构成矩阵的数据出现异常，不再满足独立同分布，故矩阵的特征值谱密度函数偏离M-P定律，由图4(a)和(b)谱密度函数与M-P定律的重合度知，线路a存在异常用电用户。

3.2 异常用户确定

线路a下共有专用变压器用户4户，根据第3.1节的分析，进一步分析线路a的4户用户。从计量自动化系统获取同时间段内每户用户的15 min有功功率数据，构建高维随机矩阵，其原矩阵维数和经式(7)变化后的矩阵维数及行列比见表2。4个高维随机矩阵协方差矩阵的特征值谱分布如图5所示，谱密度函数与M-P定律的偏移情况如图6所示。

表2 线路a各用户高维随机矩阵维度Tab.2 Dimensions ofhigh dimensional random matrix of users of line a

由图5可知，线路a中A机械制造厂、C涂料有限公司、D塑料胶制品有限公司的协方差矩阵特征值的平均谱半径基本都分布于圆环内，但B铝业有限公司的协方差矩阵特征值的平均谱半径小于内径，存在异常用电的重大嫌疑。进一步研究B铝业有限公司的谱密度函数(图6)，该用户的谱密度函数与标准M-P定律的重合率为65.8%，重合率较低。综合单环定律和M-P定律可以判断，B铝业有限公司存在异常用电情况。

3.3 异常时间区段确定

高维随机理论中，当电网正常运行、无扰动发生时，全网日用电总量协方差矩阵的特征值平均谱半径在整个观测时间区段内变化平稳，即使有波动，也是由于正常用电负荷微小波动所致。当异常发生后，协方差矩阵的特征值谱半径分别在谱半径曲线上有两个显著的突变点，分别对应异常的起止时间，总时长为两突变点之间的时间区段。

图7为线路b整条线路2015年1月至2016年7月期间总日用电量平均谱半径波动曲线，图8(a)为线路a整条线路2015年1月至2016年7月期间总日用电量平均谱半径波动曲线，图8(b)为线路a中B铝业有限公司2015年1月至2016年7月期间日用电量平均谱半径波动曲线。

图5 线路a中4个用户协方差矩阵特征值谱分布Fig.5 Spectral distribution of eigenvalues of four users’ covariance matrices of line a

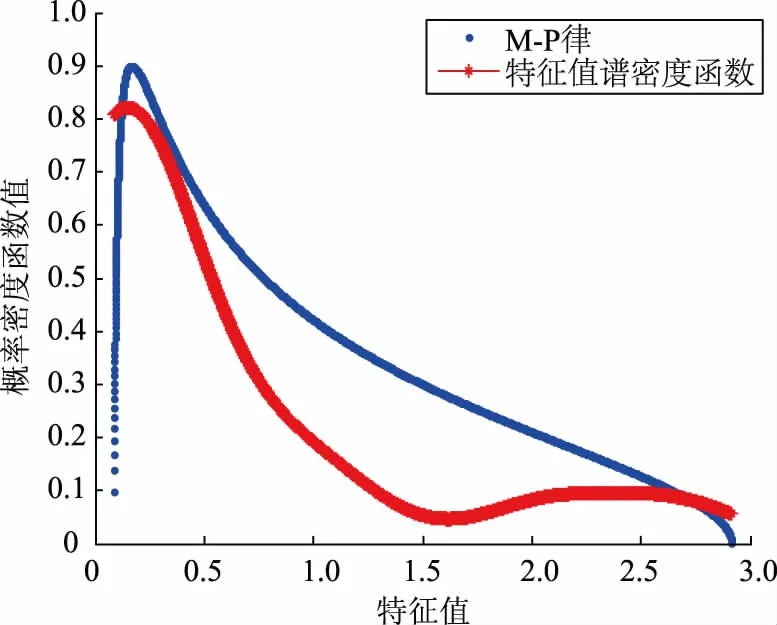
图6 B铝业有限公司谱密度函数Fig.6 Spectral density functions of B aluminum limited company

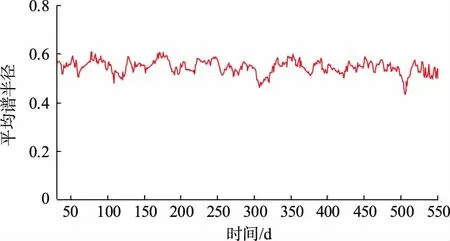
图7 线路b总日用电量平均谱半径Fig.7 Mean spectral radius of daily total electricity consumption of line b

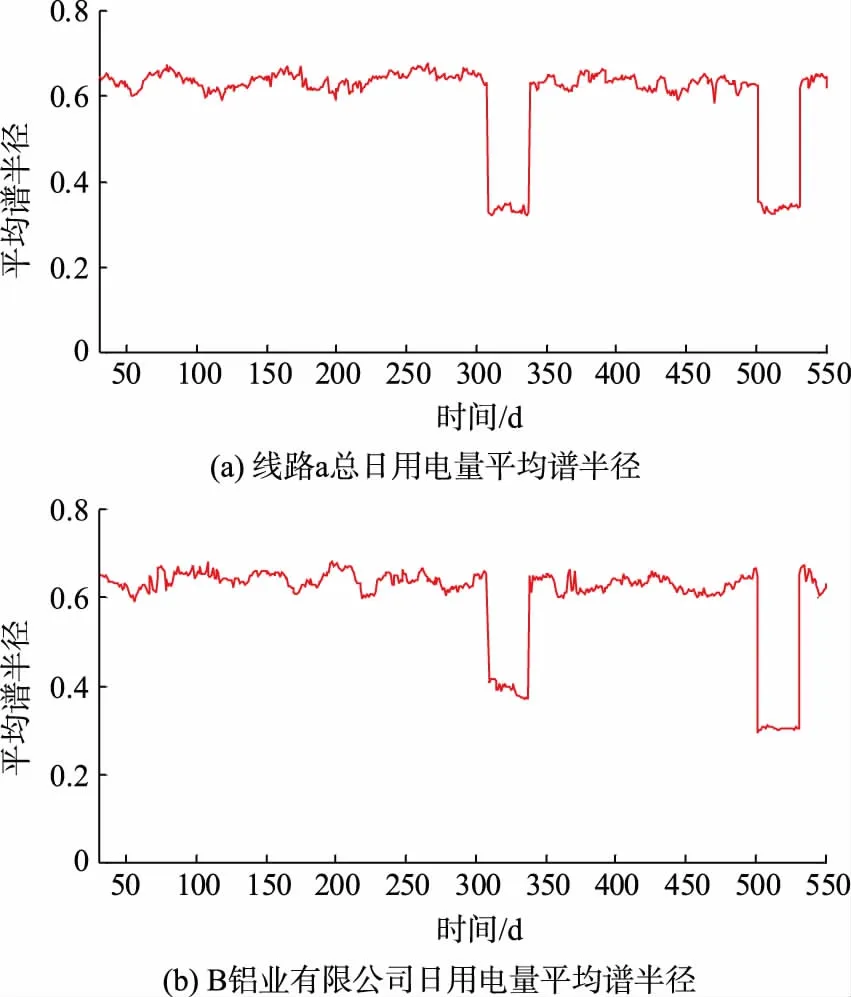
图8 线路a及用户平均谱半径Fig.8 Mean spectral radius of line a and users

对比图7和图8可知，线路b在研究时间区段内平均谱半径曲线仅水平方向呈微小波动，结合高维随机矩阵理论，线路b在2015年1月至2016年7月不存在异常。而线路a存在2个突出的突变点，不再是水平方向的微小波动，数据存在异常。如图8所示，线路a总日用电量的平均谱半径和异常用电用户日用电量平均谱半径均显示，异常起止时间分别为2015年11月至2016年5月，异常时间区段为7个月。经电力部门的实践考察与实际异常时间区段基本吻合。

用电信息采集平台采集的数据构成的高维随机矩阵的平均谱半径的变化规律可以反映系统的运行状态，并且判断出具体的异常用电时间，便于电力部门进行下一步的工作。

4 结论

本文选取电力大数据建立高维随机矩阵，提出一种基于高维随机矩阵理论的用电异常行为识别方法，实现了对用户异常用电行为的精确和可靠识别，主要做法如下：

a)计算高维随机矩阵的协方差矩阵和谱密度函数，分析特征值在复平面上的分布特性，基于M-P定律和单环定律实现对用电行为异常的精确识别。

b)基于高维随机矩阵理论，研究正常用电条件下的协方差矩阵平均谱半径波动的平稳性；通过分析用户实际平均谱半径的波动特性以及波动突变区间，确定用户异常用电的时间区段。

c)通过对某电网台区历史异常用电用户进行实例分析，验证本文所提方法能准确定位用电异常发生的线路，锁定异常用电用户，进而确定用户异常用电的时间区段。

本文所提方法能充分挖掘相关电力大数据的价值，相比传统方法，更具时效性、精确性和可靠性，具有实际工程应用价值和推广价值。