基于图论的麻灰纱混纺均匀度定量评价

石丽莉，饶樊莉

(成都纺织高等专科学校，四川 成都611731)

0 引言

目前，纺织领域评价麻灰纱质量的优劣主要集中在成纱的工艺流程研究、纤维成分、纤维杂质分析等方面，主要的评价指标有纱线断裂强度、条干均匀度、棉结数量、纱疵等等。 但是对于麻灰纱混纺均匀度、混纺稳定性的定量评价鲜有研究。 因而，利用图像进行麻灰纱混纺均匀度研究成为有意义的研究内容。

使用高倍电子显微镜拍摄出纱线横切面图像，再利用图像进行麻灰纱混纺均匀度的研究本质上是利用计算机将图像转换为数字矩阵建立模型进行测算和评价。 这种方法在其他邻域和行业已有大量的相似研究。 如：针对喷灌均匀度问题克里斯琴森(Christiansen)提出了均匀系数模型[1]，针对城市公园绿地空间分布均匀度的问题高祥伟[2]等通过网格化进行了探讨，都业宏[3]等利用径向均匀性理论讨论霰弹弹着点分布均匀性的问题，何振娟[4]等利用分形理论讨论复合材料中颗粒分布均匀性的问题，等等。 由于研究对象的不同、图像的差别、理论和技术等多方面的原因，虽然众多学者在其研究领域均取得了一定的研究成果，但还没有一个公认的对二维图像颗粒均匀度定量评价的最优标准和分析方法。

本文研究利用图论的最小生成树理论，通过颗粒间理想距离的定义，建立了基于图论的麻灰纱混纺均匀度定量评价模型。 该方法应用到麻灰纱横切面图像的黑纤维分布均匀度讨论中，取得了满意的效果。

1 二维平面中颗粒间理想距离的定义

罗传文在文献[5]中对平面点集的均匀度进行了定义。 假设在一个长方形内有a × b ＝n 个均匀分布的点，点与最邻近点之间的距离均为s，称这样的格局称为二维完全均匀格局，如图1。

图1 完全均匀格局

根据二维完全均匀格局的定义，下面给出了颗粒间理想距离的定义。

定义1 所谓理想距离，就是在有限平面矩形范围内，点与最邻近点的距离均相等，且满足点的数量n 与理想距离的平方d2的乘积n × d2恰好等于该矩形面积S，即S ＝n × d2也即

定义2 在有限平面矩形范围内，点与最邻近点的距离均为零，即点全部聚集收拢为一点，称为完全聚集。

2 最小生成树的基本概念

图论起源于18 世纪欧拉(Euler)对七桥问题的抽象和论证，是运筹学的分支。 它广泛地应用于实际生活、生产和科学研究中，有很多问题可以用图论的理论和方法来解决。 近年来，图论在图像处理方面的研究常见于对图像分割算法的应用，如参考文献[6-7]等等。 但是，将图论运用在颗粒均匀度分析上少有研究文献，成为一个值得探讨的新的研究方法。

给定一个有权无向连通图G ＝(V，E，w) ，其中V 代表图中点的集合， E 代表连接节点的边的集合，连接u，v 两点的边均赋予权值为w(u，v) 。 由图生成的连通且不含圈的无向图称为生成树。 显然，一个有n 个节点的树，其树枝(边)的数量为n- 1。

假设T ＝{t1，t2，···，tk} 为图G 的所有生成树的集合。 无向连通图G ＝(V，E) 的最小生成树就是满足联结所有顶点的边的权值和最小(即时的子图T，此时T 无回路且连接所有的顶点，所以它必须是棵树。 最小生成树即最小权重生成树，其算法在很多邻域都有着重要应用。

最小生成树算法主要有Kruskal(克鲁斯卡尔)算法和Prim(普里姆)算法。 其中，Kruskal 算法步骤为：

(1)选择边e1，使得w(e1) 尽可能小；

(3)当第(2)步不能继续执行时，则停止。

不论选取哪种算法，当起始顶点不同或有两条相同最小权值的边可选择时，构造的最小生成树不一定唯一。 但若给定算法，则唯一。 同时，最小生成树的边的权值总和是唯一的。

3 麻灰纱纤维均匀度定量评价模型

如果将二维平面内的点看成是图的顶点，点的连线看成图的边，点与点之间的距离视为边的权，点的分布均匀度问题就转化为图论的最小生成树问题。

根据最小生成树理论，在二维完全均匀格局中，最小生成树的总边长唯一确定，且等于(n - 1)× d。 对于麻灰纱纤维图像来说，平面上分布的黑纤维点之间的最小生成树构成纤维颗粒间“最紧”支撑。 在研究区域内，当被测纤维数量一定，其树的边权大小决定纤维分布的松紧关系。 模拟在同一区域内取三幅数量相同的点图，呈不同疏密程度，经过最小生成树计算，对比如图：

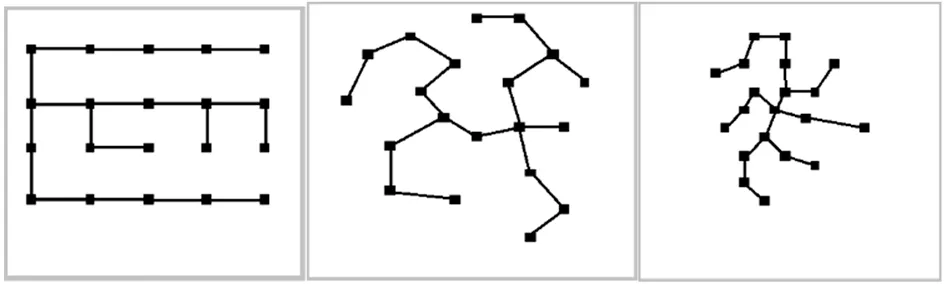
图2 最小生成树图

由此，给出判断纤维分布均匀度定量评价模型：

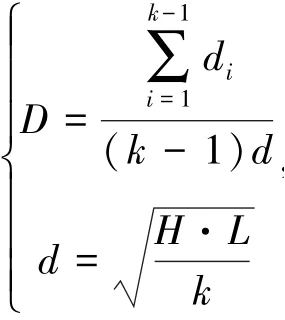
其中di指构成该图最小生成树的边权，d 指满足完全均匀格局时的最小生成树的边权，H，L 分别指观测区域的高度和宽度，k 为纤维数量。 模型通过计算图像中纤维的最小生成树权总和与完全均匀格局下最小生成树权总和之比，定量评价纤维分布的聚集和分散状态。

显然，当点满足二维完全均匀格局时， D ＝1(如图3)；当满足完全聚集时，D ＝0。

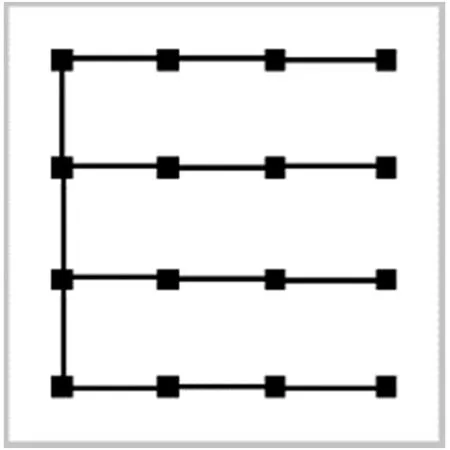
图3 完全均匀格局下的最小生成树图

图3 的模拟点图，经公式(1)计算， D 值分别为：D1＝0.8944，D2＝0.7105，D3＝0.4638。 计算结果与图像的均匀分布状态完全一致。

模型说明：

(1) D 值越趋近于0，说明分布越密集，D 值越趋近于1，说明分布越均匀。

(2)一般情况下，研究的点应在该点的理想区域内。 如果点的分布超出理想区域，且分布较均匀，D 值有可能大于1，此时点向外均匀发散。 如图4，黑色边框为理想区域，灰色边框为观测区域。图4 计算得出D ＝1.25。

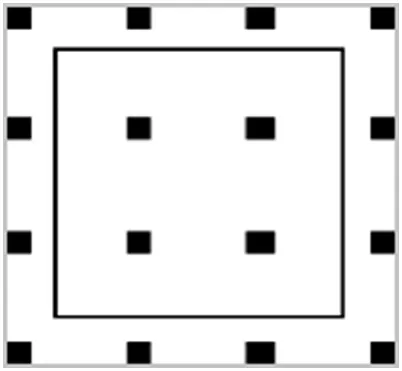
图4 超出理想区域的分布

4 实例讨论

实例研究选取放大倍率为1000 的麻灰纱纤维切片，模型的计算采用Matlab 编程运算实现，通过计算结果进行对比，对麻灰纱纤维的分布均匀度进行定量评价。

4.1 麻灰纱图像的均匀度定量比较

选取四幅不同的麻灰纱纤维切片图，利用图像分割技术和网格化对黑纤维计数和定位对比如图5。

图5 麻灰纱纤维切片图及黑纤维定位图

从左至右D 值和纤维数量n 依次为：

表1 D 值和纤维数量n

通过D 值对比可以明显看出，图中“1”的均匀度最好，且黑纤维数量最多。 “4”的均匀度最差，黑纤维数量最少。

4.2 不同批次麻灰纱均匀度定量比较

实验选取A、B、C 三个批次不同的麻灰纱切片样本，参考文献[8]的评价方法，通过三个方面进行麻灰纱定量评价。 样本如下图：

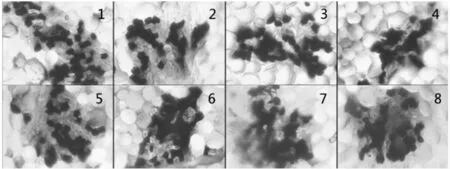
图6 A 批次样本

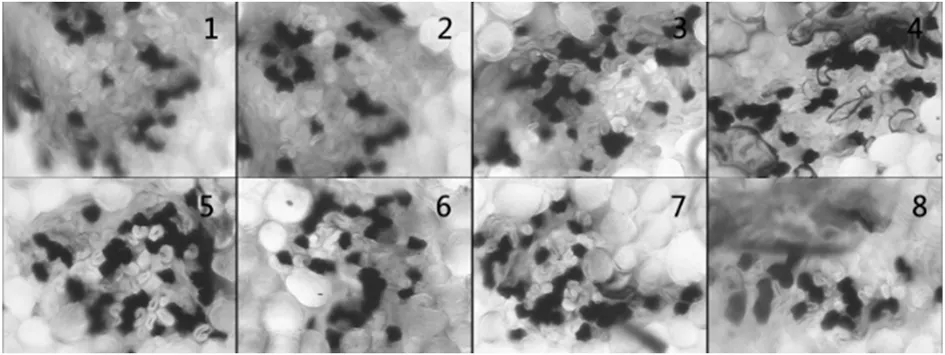
图7 B 批次样本

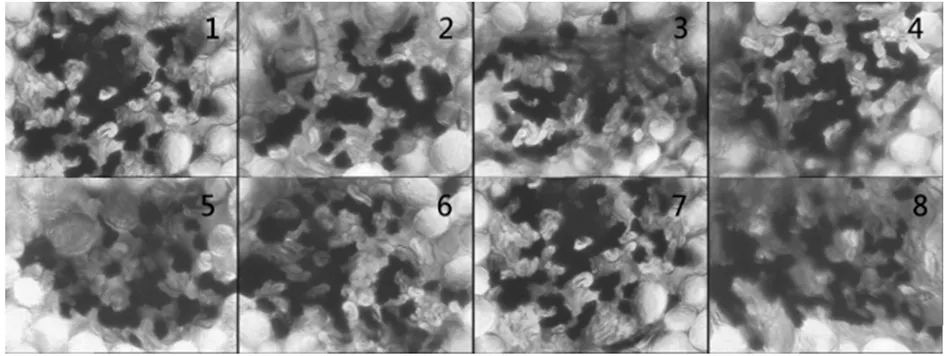
图8 C 批次样本

4.2.1 整体均匀度

对于不同批次的麻灰纱整体均匀度定量评价，可以对每个批次样本D 值线性拟合，拟合直线的相对位置说明其整体均匀度的优劣。

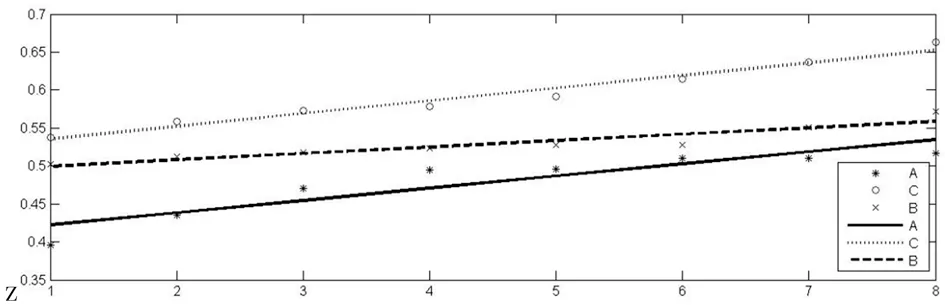
图9 三批次样本拟合曲线

三组样本按D 值线性拟合结果为：

样本A：y ＝0.01606x ＋0.4063

样本B：y ＝0.008444x ＋0.4911

样本C：y ＝0.01672x ＋0.5189

由图9，整体均匀度从高到低依次为：C＞B＞A。

4.2.2 均匀分布的稳定性

拟合直线的斜率代表每组纱线样本均匀度变化的快慢。 拟合斜率越小，表示某批次或工艺的纱线越均匀越稳定性。 因此，三组样本的均匀分布的稳定性从高到低依次为：B＞A＞C。 其中样本A 与C的稳定值非常接近，用人工检测无法准确判断。

4.2.3 黑纤维所占比例的稳定性

不同批次的麻灰纱黑色棉纤维在切片样本中所占比例的稳定性，可以用样本黑纤维数量的标准偏差来评价：

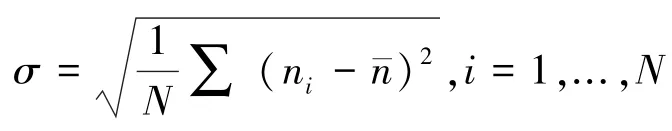
N 为每个批次的样本数量，ni为每个样本黑纤维数量，n-为该批次样本黑纤维数量均值。

再对标准偏差作无量纲化处理：

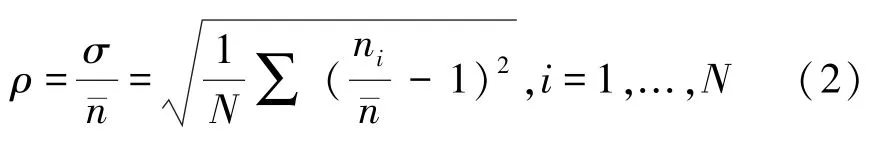
ρ 值可用于判断某批次样本黑纤维所占的比例的稳定性，ρ 值越小说明黑纤维所占的比例越稳定性。

通过对三组样本ρ 值的计算，比较如下：

C( ρ ＝0.1256) ＜A( ρ ＝0.1522) ＜B( ρ ＝0.2359)

数据说明样本C 的黑纤维所占比例最稳定，其后依次是A、B。

实验对三个批次的样本在整体均匀度、均匀分布的稳定性、黑纤维所占比例的稳定性三个方面的进行了测算，定量分析比较了结果。 同时，对于每个批次样本的综合性评价，可以根据实际需要对每个方面赋予权重，得出综合定量评价。

5 结论

基于图论的最小生成树原理建立的麻灰纱均匀度定量检测模型，通过对样本的D 值计算和ρ 值计算，可以完成单个样本均匀度定量评价、样本组的整体均匀度、均匀分布的稳定性、黑纤维所占比例的稳定性的定量评价，实现了麻灰纱均匀度定量检测。 检测利用MATLAB 实现了全程自动检测计算。 在样本、参数一致的条件下具有计算结果稳定、计算速度快、评价量化明确，无人为因素干扰等等的优点。 经过实验验证，该模型以及基于模型的评价方法能较好地实现对麻灰纱均匀度的定量评价，一种新颖且有效的评价模型。