电偶腐蚀下非稳态扩散瞬时静电场分析
2019-06-19王向军张建春徐庆林
王向军,张建春,徐庆林
(海军工程大学 电气工程学院, 湖北 武汉 430033)
处于海水中的舰船会因金属的不同材质而发生电偶腐蚀产生腐蚀电流,在海水中产生腐蚀电位和腐蚀静电场、轴频电场[1-5]。电解质流动状态一定时,金属接触电解液发生电化学反应后,电流达到稳态前,物质的传递首先经历一段时间的非稳态扩散过程[6-7],最终达到稳态。由于海水中的氧含量相对较高,在非稳态过程中会产生较强的腐蚀电流密度,这个过程在分析静电场特性时是不能忽视的,并且在电解质流动的情况下电极会不断接触新鲜氧气产生浓差极化,这可能会导致金属的电偶腐蚀始终处于非稳态过程。
此外,在实际测量过程中,海水实际流动状态对船体的冲击及与海水的实际接触面积是不断变化的,从而导致电化学腐蚀的稳态扩散不断被破坏,测量到的始终是非稳态扩散情况下的静电场。因此,分析腐蚀电场的非稳态扩散时间能够为进一步研究舰船静电场特性提供新的理论基础。
1 非稳态扩散数学模型
由于腐蚀发生在固液界面上,所谓静止的电解质主要针对电极表面而言,包括全部溶液处于静止状态,或在流动的溶液中电极周围表面层中的对流传质速度可忽略的情况。当静止的溶液中存在大量的反应粒子时,反应粒子向电极表面的传质方式主要以扩散为主。金属板处于静止溶液中的模型如图1所示。
粒子在金属板表面的扩散过程满足斐克第二定律:
(1)
式中:ci为i粒子在溶液中的浓度,Di为i粒子的扩散系数,x为距离金属板表面的径向距离。
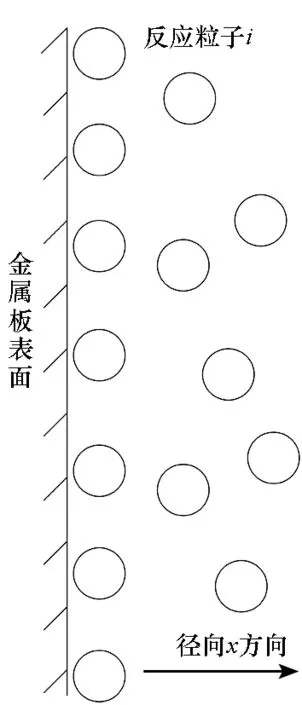
图1 电极表面非稳态扩散Fig.1 Non-steady-state diffusion on plate
1.1 求解条件的设定
分析非稳态扩散过程时,得到各处i粒子浓度随时间的变化ci(x,t)。根据斐克第二定律并设置边界条件便可得出ci(x,t)。其边界条件及初始条件[7]为:
1)粒子扩散系数Di=常数,即扩散系数不随扩散粒子的浓度变化。
2)腐蚀反应开始前的粒子浓度均匀分布在溶液中,即初始条件为ci(x,0)=c0,c0为溶液中i粒子的初始浓度。
3)开始反应后,溶液中i粒子的浓度不发生浓度极化,为了区分反应前后溶液中i粒子的浓度,假设此时溶液中的浓度为cs,则此时的边界条件可设定为ci(∞,t)=cs。
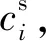
1.2 电偶电极表面电流密度推导
为了得到电流密度的解析解,应对i粒子在垂直于金属表面x方向上的浓度分布进行求导。求解非稳态时的浓度分布时,从斐克第二定律出发,应用拉普拉斯变换即可求出[8]。对式(1)两边进行拉普拉斯变换得:
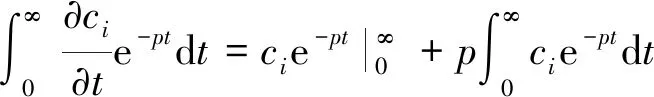
(2)
(3)
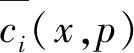
将初始条件2)代入式(2),并将式(1)以象函数替换得:
(4)
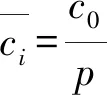
(5)
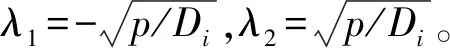
对边界条件进行拉普拉斯变换得:
(6)
i粒子的浓度象函数可由式(5)、式(6)得到。
(7)
对式(7)进行拉普拉斯逆变换可得:
(8)
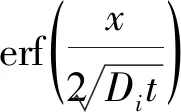
当i粒子在金属表面完全反应时,令扩散系数Di=10-5cm2/s,不同时间下金属表面层中反应粒子浓度极化的发展如图2所示。
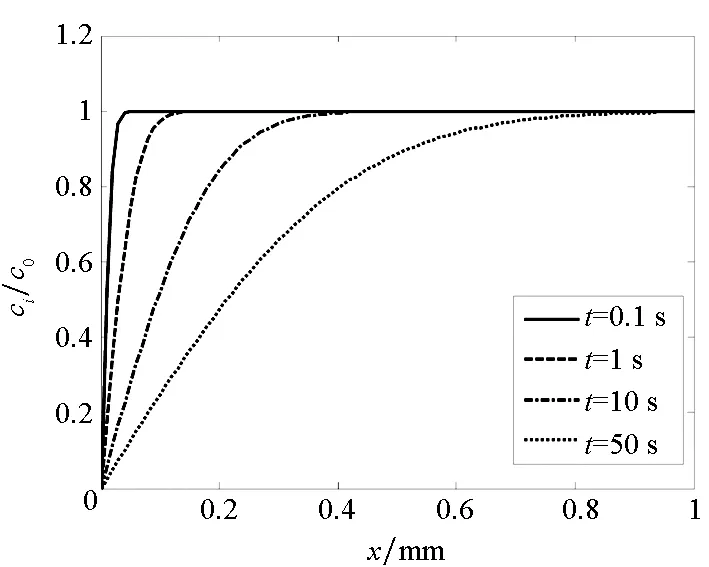
图2 反应粒子浓度分布Fig.2 Distribution of i concentration
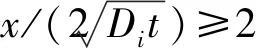
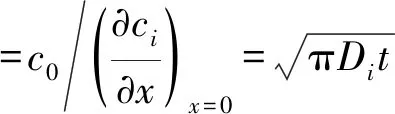
(9)
根据式(8)和图2还可以看出,任意一点的ci值都是随着时间的增加而不断减小的,从而致使浓差极化的扩散层厚度逐渐增加,经过一段反应时间后电极表面的氧浓度逐渐趋于0,在金属表面附近的溶液中氧的浓度梯度达到最大值,此时扩散层的厚度不再随着氧的浓度变化而变化。
由热力学中的法拉第定律可知,非稳态扩散下的瞬间电流密度为:
(10)
式中:νi为i粒子的反应数,n为反应过程中电子的转移数,F为法拉第常数。电流密度随时间的变化曲线如图3所示。
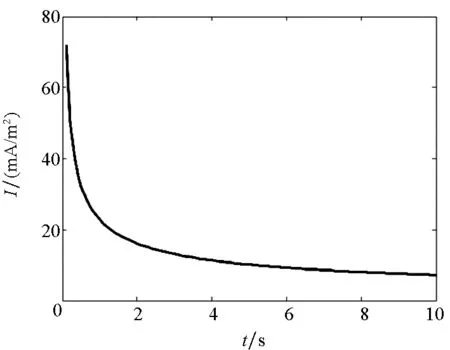
图3 电流密度随时间的变化Fig.3 Change of current density over time
由图3可知,在2 s前电流密度随时间的增加迅速减小,在4 s后电流密度逐渐趋于稳态,随时间的变化不是很大。这主要是由于i粒子在浓度极化过程中离子的瞬时有效扩散厚度逐渐增加,离子到达反应电极表面的难度增加,从而会抑制反应的进行使电流密度减小。
根据式(10)可知,在平面电极上不可能建立稳态电流。但一般情况下,液相与固相之间的传质总是存在对流现象,因此只在扩散作用下导致的传质过程一般不会延续太长时间,一旦瞬时有效扩散层厚度δ有与对流作用下产生的扩散层有效厚度近似或相等时,电极表面的传质过程逐渐转为稳态[7]。
1.3 电极板电流密度“有效长度”
在电解质溶液中,当不同电极电位的金属相互接触时,电位较低的金属会充当阳极发生氧化反应,而电位较高的金属为阴极发生还原反应[9]。当电偶对处于NaCl溶液中时,阴极的还原反应主要与电解质溶液中的氧发生反应,此时电偶对在达到稳态电位之前产生的腐蚀电流是由氧的扩散所决定的,其瞬时电流密度可由式(10)表示。
由于电解质溶液吸附在电极表面时产生溶液电阻,腐蚀电流能够传导的距离会受到该电阻的限制,将电流产生到减小为零的距离称为“有效距离”[10-11]。发生反应的电极材质及导电性能的差异,导致在不同电极表面上的“有效长度”也有所不同。假设在阴极表面产生腐蚀电流的有效长度为l1,阳极为l2。为了验证由于扩散传质在溶液中产生的电流密度及扩散层有效厚度的正确性,并排除对流传质对理论推导结果的影响,发生电偶腐蚀原理如图4所示,其中阳极水平放置,阴极垂直放置。
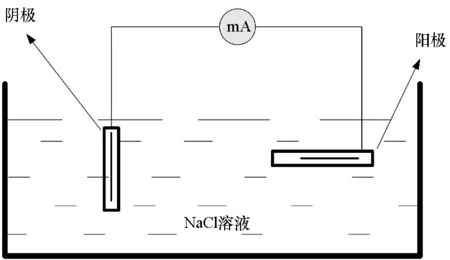
图4 电偶腐蚀原理Fig.4 Principle of galvanic corrosion
2 静电场分布求导
为了得到由于电偶腐蚀下电流密度在电解质溶液中任意位置产生的电极电位及静电场,将相同规格的金属板表面产生的腐蚀电流等效为电流线进行建模。根据图4电偶腐蚀的原理图中金属板放置位置的不同,分别将阳极等效为垂直电流元,阴极等效为水平电流元,建立如图5所示数学模型。
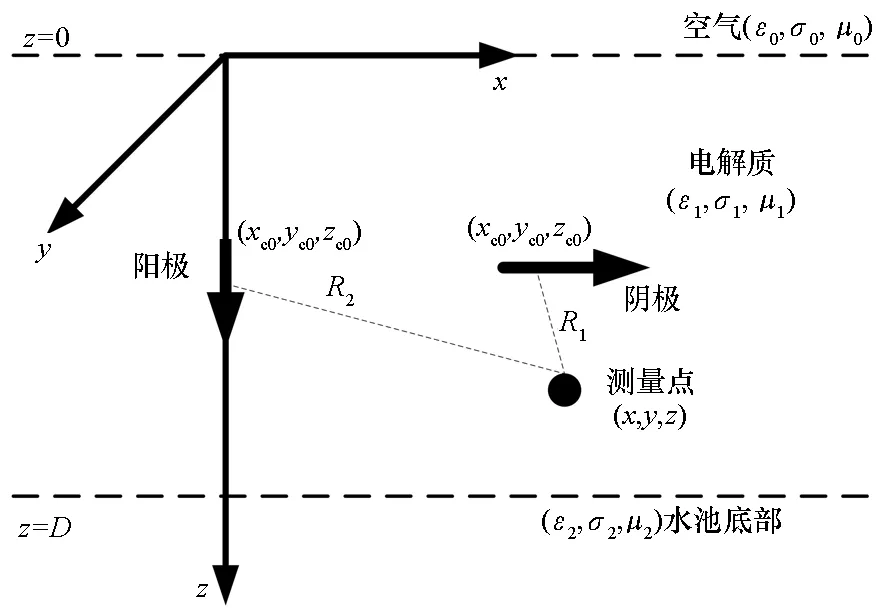
图5 电偶腐蚀电流线模型Fig.5 Current model of galvanic corrosion
在图5中,假设电解质溶液的深度为D,并将阳极、阴极的有效电流密度长度分别设定为l2、l1。为了得到电流密度在电介质中任意位置产生的电极电位及静电场,采用电流元在三层介质的海水中产生的电位解析表达式[12-14],在电解质溶液中任意位置处产生的电位为两个电流线的叠加。
从而可推导出该模型在电解质任意位置处产生的电位为:
φ(x,y,z)=
(11)
其中:η=(σ1-σ2)/(σ1+σ2),σ1为海水中的电导率,σ2为海床电导率;Ia、Ic分别为阳极和阴极的瞬时电流密度,由于在发生电偶腐蚀时,两电极以导线连接且面积相等,因此两电极在反应时产生的电流密度相等,即Ia=Ic=I。
r1βk=(x-xβ0)i+(y-yβ0)j+(z-2kD+zβ0)k
r2βk=(x-xβ0)i+(y-yβ0)j+(z-2kD-zβ0)k
r1βm=(x-xβ0)i+(y-yβ0)j+(z+2mD-zβ0)k
r2βm=(x-xβ0)i+(y-yβ0)j+(z+2mD+zβ0)k
其中:β代表阴极和阳极下标a、c。
根据电磁场相关理论可知,介质中任意点位置处的电场强度分量等于该点的电位梯度的负数。则在电解质中产生的静电场三分量为:
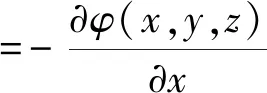
(12)
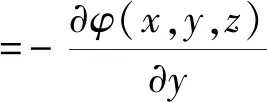
(13)
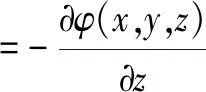
(14)
3 算例分析
为了便于实验验证,以钢板和铜板作为研究对象,将其置于电导率为4 S/m电解质溶液中,金属板位于电解质深0.5 m处,铁板在电解质中发生阳极反应Fe→Fe2++2e-,铜板发生阴极反应4e-+O2+H2O→4OH-。假设电解质中的氧的饱和浓度为6×10-6mol/L,氧的传递系数DO2≈0.043 57 cm2/s。测量点在(0,0,1)处产生的电位及电场分布如图6所示。
在非稳态过程中,由于电极表面发生腐蚀所需要的氧的浓度会随着时间的变化而变化,整个体系中产生的腐蚀电流密度会受到阴极表面氧的还原速度的控制。在该反应步骤的控制下,电解质中固定点位置处的电场分量及电位分布随时间的变化曲线如图6所示。同时在电解质中产生的电场及电位的分布是由电偶腐蚀电流产生的,当电流密度发生变化时,其电场及电位也会发生变化。
腐蚀电偶对处于非稳态扩散过程时,电场分布及电位分布均随着时间的变化而减小,最终会达到一个稳定值。根据电化学中的介绍,当在非稳态扩散过程中达到稳定值后,电偶对的腐蚀反应将会进入与时间无关的稳态扩散过程,使腐蚀电偶对的电位最终达到一个稳定电位。根据图6可知,电场分量及电位均在7 s左右逐渐趋于稳定。
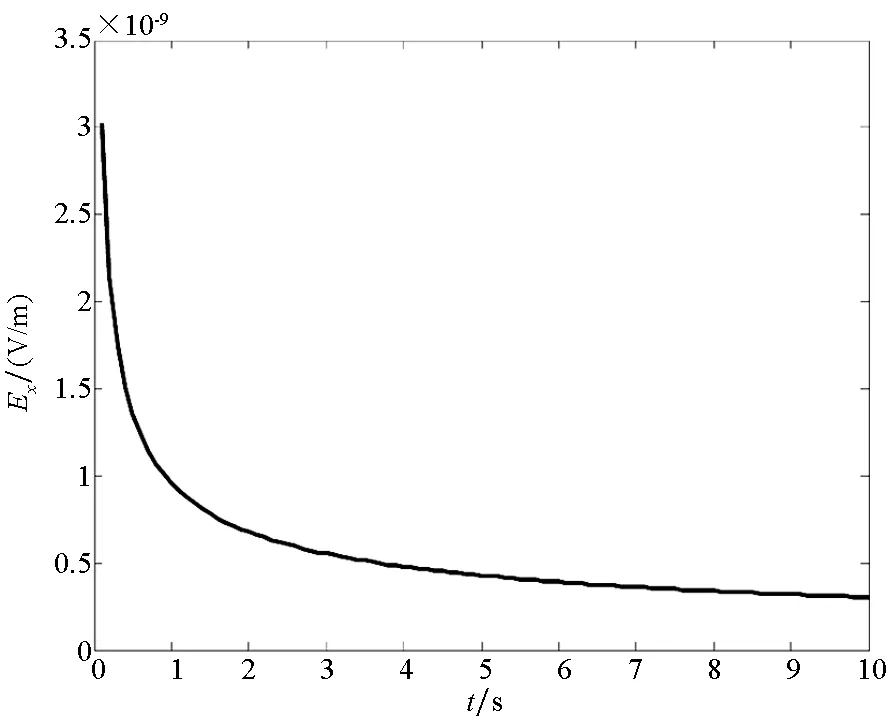
(a) 电场Ex分量(a) Electric field of Ex
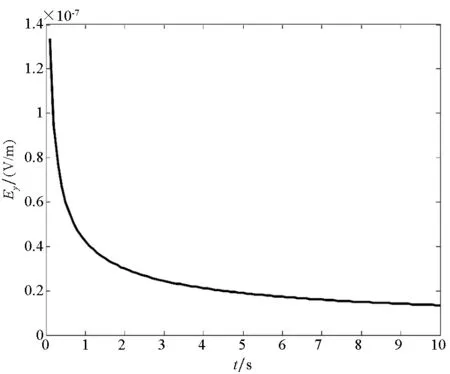
(b) 电场Ey分量(b) Electric field of Ey
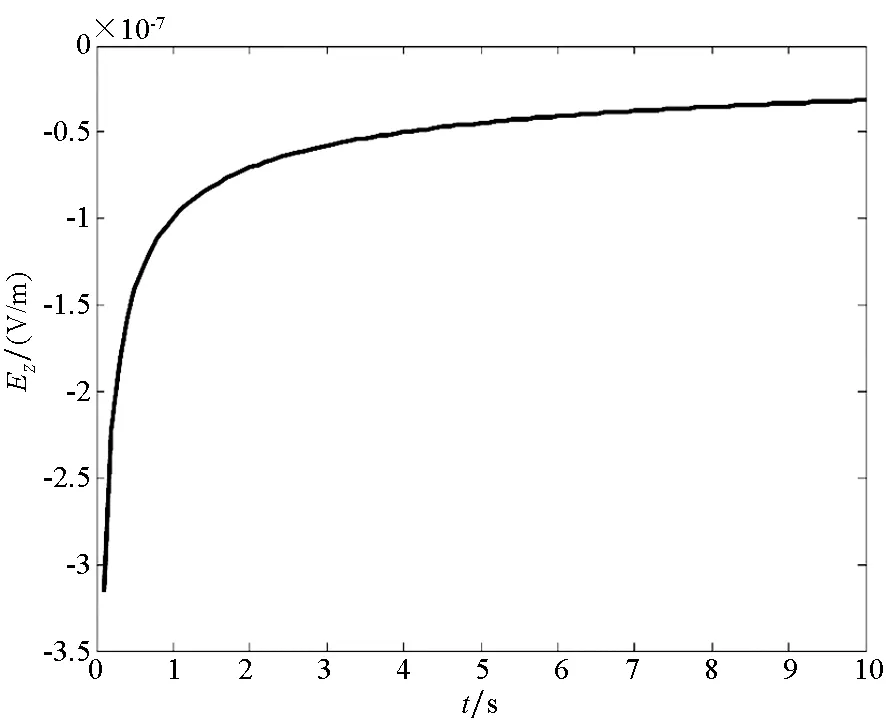
(c) 电场Ez分量(c) Electric field of Ez
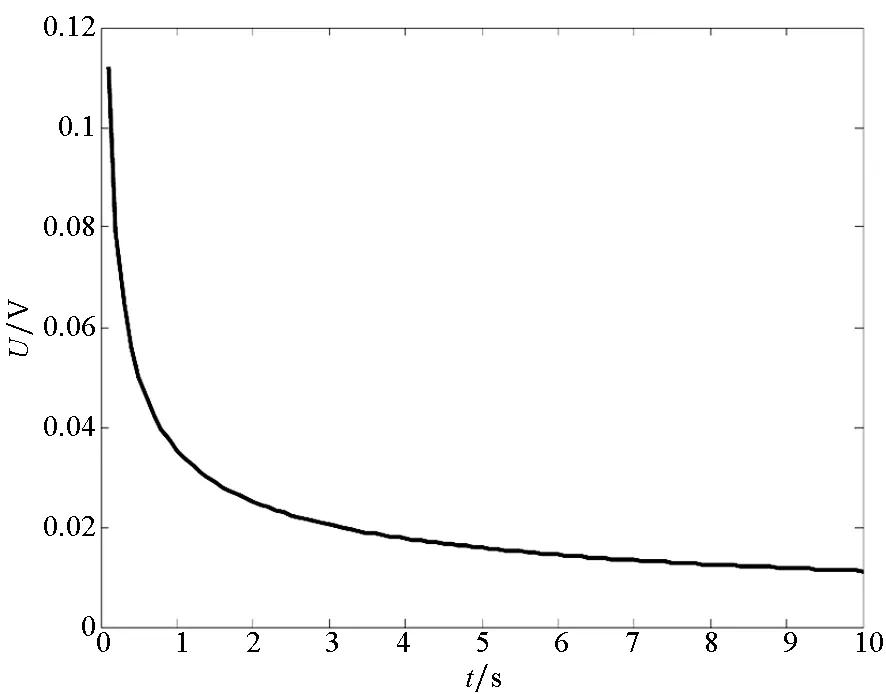
(d) 电位分布(d) Distribution of potential图6 非稳态扩散过程电场分量及电位分布Fig.6 Electrical field and potential distribution in unsteady diffusion process
当前对电场的实验测量主要以测量电场模值为研究对象,为了更好地观察电场在非稳态过程中的变化趋势,给出如图7所示的电场模值随时间的变化图。由图7可知,随着时间的变化,电场模幅值随着时间的变化而减小,最终达到一个稳定值,其原因与上面介绍的原因相同。
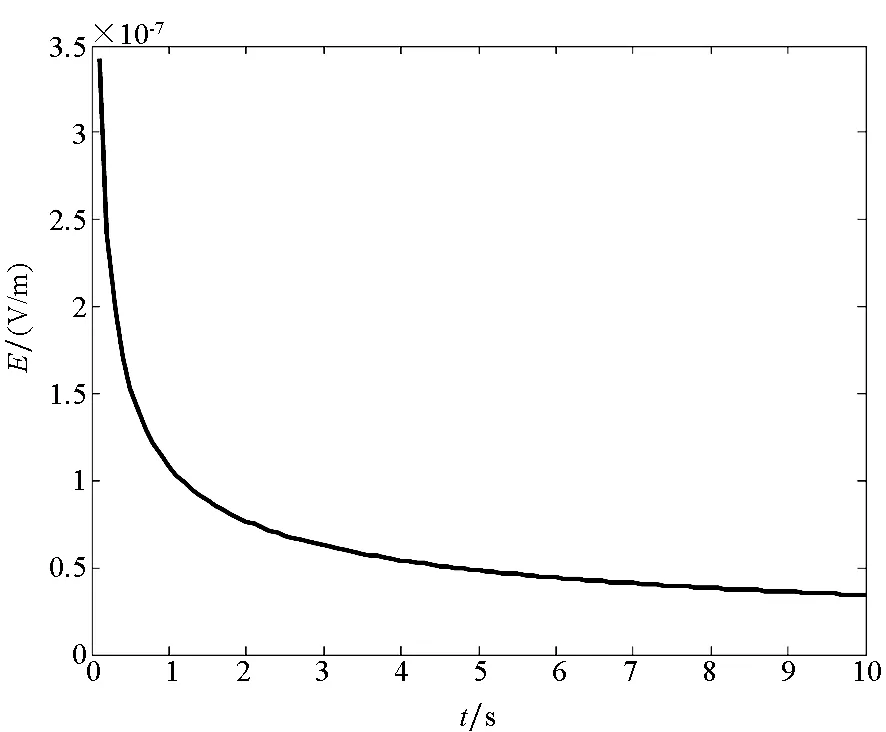
图7 非稳态过程下的电场模值分布Fig.7 Electric field values in non-steady-state
4 仿真结果与实验对比
在规格为10 m×5 m×1 m的水池中分别水平和垂直放置规格为0.3 m×0.2 m×0.02 m且除底面外其余表面涂有绝缘漆的由武汉钢铁生产的型号为AH32的铁板及型号为GB1176的铜板作为研究对象。两块金属板与电解质溶液的有效接触面积均为0.3 m×0.2 m。在水池中配制电导率为4 S/m的NaCl溶液,金属板之间以导线连接,接触处防水性良好。两金属板之间的极距约为2 m,电场传感器置于水池底部,距离两金属板的垂直距离均为0.3 m,放置位置如图8所示。
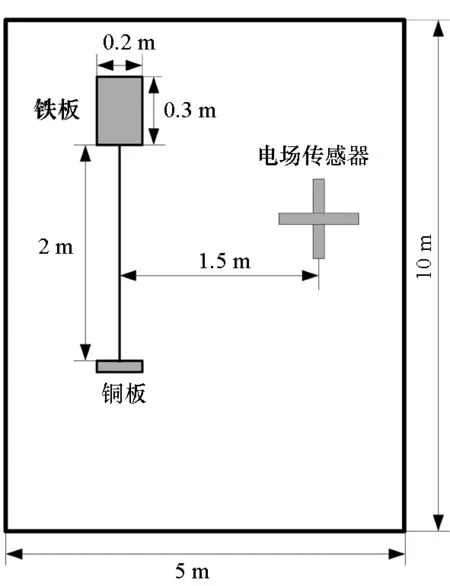
图8 实验设施位置及尺寸分布图Fig.8 Location and size distribution of experimental facility
当金属板放入电解质溶液中时,对其电场及电位分布进行测量,实验结果与仿真结果对比如图9所示。
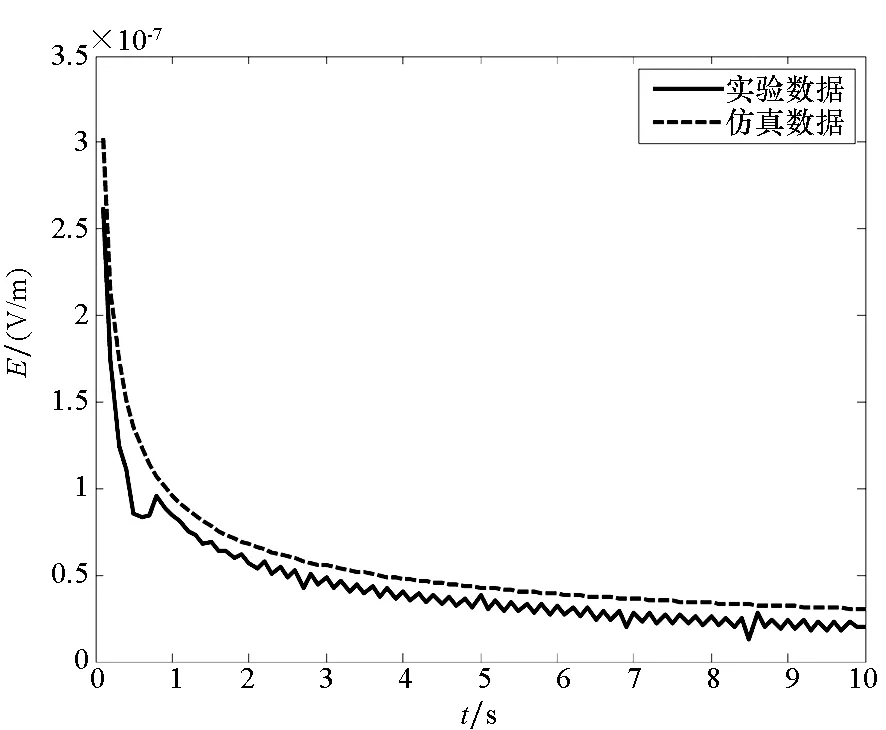
(a) 电场模值实验与仿真对比(a) Electric field comparison
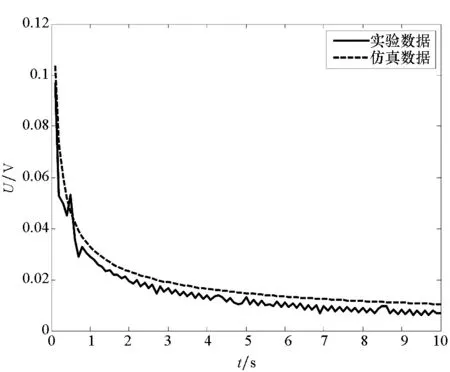
(b) 电位实验与仿真对比(b) Potential comparison图9 实验与仿真结果对比Fig.9 Comparison between experiment and simulation
由于水池处于封闭的室内环境,为了减小实验误差,使实验环境与仿真环境近似,实验前,对水池中的溶液通入氧气,使溶液中的氧含量达到饱和。实验过程中,保持实验测量装置处于开启状态,当金属板放置于溶液中时对实验数据进行采样分析。在实际测量数据中由于外界环境及溶液波动会对实验数据产生干扰,为了得到较为准确的实验结果,对实验数据进行了低通滤波处理。
由图9可以看出,不同的金属板在电解质溶液中得到的电位分布与电场模值的曲线走势基本一致,在1 s之前实验结果出现奇异值,这主要是由实验传感器精度造成的,传感器在采样频率固定的情况下不能对衰减较快的电场幅值进行采样,最终会导致奇异值的出现。而在2 s后电场幅值及电位不会发生较大衰减情况并达到稳态,进入稳态腐蚀过程。这主要是由于裸露金属与溶液接触时,电化学反应较为剧烈,电解质中的氧能够充分与铜接触发生反应,产生的腐蚀电位及电场模值较大。经过一段时间的反应后,在金属板附近产生的反应产物的浓度增加,同时在铁板表面形成一层含有Fe(OH)2的氧化膜,阻止铁原子的阴极还原反应。此时氧在铜表面得到的电子主要来源于Fe2+的氧化反应,使Fe2+氧化成Fe3+,使其在铁表面形成固态产物Fe(OH)3,保护铁的进一步腐蚀,从而使电化学体系下的反应速度下降。
5 结论
在电化学反应的基础上,对非稳态扩散过程下每个金属板上的腐蚀电流密度进行求解,并通过电流密度运用较为成熟的电流元方法推导出电解质中的腐蚀电位及静电场随时间的分布情况。仿真结果及实验结果表明:金属在电偶腐蚀非稳态扩散传质过程中产生的腐蚀电位及静电场会随着时间的增加而减小,非稳态过程持续的时间很小。
