干扰及机动条件下的比例导引智能调控策略

徐 洋，方洋旺，伍友利，杨鹏飞，张丹旭

(1 .空军工程大学 航空工程学院， 陕西 西安 710038； 2. 军事科学院 评估论证研究中心， 北京 100091)

随着电子科技的发展，信息化背景下的现代战争环境逐渐趋于复杂化、作战目标及干扰样式逐渐呈现多样化。为适应未来空战的发展需求，提高复杂环境下的精确打击能力是制导武器研制重要的攻坚方向，而精确制导技术就是其中的关键所在[1]。

精确制导技术，即导弹利用自身导引头或其他外部设备探测到的目标信息，通过某种导引规律计算出合适的制导指令并作用于飞行器控制系统，从而改变导弹飞行轨迹，实现对目标的精确跟踪和有效打击的一种技术。其中，比例导引(Proportional Navigation, PN)应用最为广泛，但其对于机动目标及红外干扰情况的打击性能不足。由此，学者们也不断提出它的改进版，其中一类就是利用神经网络对其进行修正。这类方法可分为在线补偿和离线训练-在线预测。

针对在线补偿的方法，文献[2]通过构建一个专门的在线神经网络结构用来分析闭环制导律，修正PN制导指令。文献[3]基于最小化脱靶量准则，利用径向基函数(Radial Basis Function，RBF)网络在线实时调整比例系数，进而产生最优加速度指令。仿真结果表明该方法可明显减小脱靶量。为提高算法整体效率，文献[4]提出了一种基于粒子群优化(Particle Swarm Optimization, PSO)算法的多模PN。它通过利用一定的控制规则，实时切换PN和PSO算法求解导弹加速度。虽然上述方法都取得了不错的效果，但神经网络的实时训练问题属于复杂问题，时效性更是难以保证。而在线寻优算法更是无法满足制导系统对时效性的要求。

针对离线训练-在线预测法，文献[5]设计了一种基于广义回归神经网络的动态最优制导律用以追踪机动目标。通过利用遗传算法离线搜寻最优发射时机，然后在线依据弹目相对态势信息选择发射时机。在此基础上，文献[6]设计了一种带有前置误差角补偿项的PN，利用微分进化策略在线预测补偿项中的系数。上述方法的实效性明显优于在线修正方法，虽然其存在预测偏差问题，但通过增加样本数量及引入避免过拟合的方法，可获得较好的预测效果。

1 弹目红外对抗模型

笛卡尔坐标系下，导弹、目标的三维质点模型及相对运动关系如图1所示。

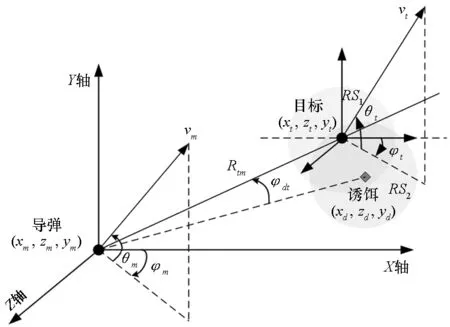
图1 三维导弹-目标相对几何关系Fig.1 3-D missile-target engagement geometry

导弹及目标的运动方程分别为

(1)

(2)

(3)

(4)

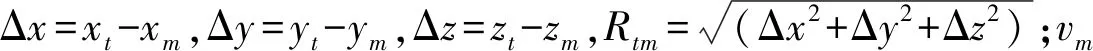
本文利用文献[7]中单线组(Single Line Group，SLG)谱带模型以及文献[8]中的计算流体力学(Computational Fluid Dynamics,CFD)方法分别离线计算目标及诱饵的辐射强度，然后在线通过差值获取。

1.1 目标机动模型

本文主要采用如下三种机动样式：水平面正弦机动；纵向平面急转弯机动；纵向平面开关机动，对应的加速度形式为：

ayt=n·g·sin(wt)

(5)

apt=n·g

(6)

apt=n·g·sign{sin[w(t-t1)]}

(7)

式中，n=9表示目标最大可承受过载；1/t1为开关切换频率；w为目标机动频率。设Rd为告警距离。当Rtm=Rd时，目标机动并投掷诱饵以摆脱载机的锁定。此过程中载机即可利用观测数据解算出与干扰相关的一些信息，如诱饵投掷间隔及目标机动样式。

1.2 诱饵干扰模型

诱饵运动模型只考虑空气阻力和重力，具体形式可参考文献[9]。而在实际干扰模型中，诱饵投掷参数很多，如单次投掷数量、投掷组数、组间间隔、投掷时机以及投掷方向。然而，考虑到战场下诱饵使用方式及仿真分析的可行性，本文假设诱饵以单枚单组方式投掷，共投掷10枚，投掷方向为垂直于飞机纵轴向上，投掷时机选为目标机动时刻，并选择投掷间隔及投掷速度作为分析变量，其变化区间分别为[0.1 s，1 s]及[25 m/s，40 m/s]。

1.3 导引头抗干扰模型

对于机动目标，导弹可通过选用适当的导引律缓解因过载限制而导致的跟丢问题；而对于红外诱饵的干扰，导引头则需要利用抗干扰算法识别目标。为此，本文采用基于遮盖效应的识别模型[10]。

首先定义遮盖效应：辐射源的红外辐射范围彼此覆盖，即RSi∩RSj≠∅。当目标与诱饵间发生遮盖效应或φdt<φ0时，其中φ0表示导引头的角分辨率，导引头因无法识别目标会跟踪辐射源的等效能量质心。当目标与诱饵分离后，导引头利用识别算法对目标加以识别。此处为避免复杂的信号处理流程，故对识别算法进行了如下简化：当Rtm>5 km，导引头处于点源跟踪阶段，此时导引头正确识别概率近似为80%；当Rtm<5 km，导引头处于成像跟踪阶段，此时正确识别概率近似为95%。经与实测数据的比较，该简化模型的识别精度与实际情况的误差小于15%。

2 优化算法及网络框架

2.1 QPSO算法

为了确定不同干扰样式下的最优比例系数及发射距离，本文采用量子粒子群优化(Quantum Particle Swarm Optimization, QPSO)算法[11]。该方法克服了PSO容易陷入局部最优解以及搜索范围受速度大小限制的局限，采用量子δ势阱的束缚态建立粒子位置更新模型，如式(8)～(11)所示，QPSO只有位置更新没有速度更新，进化方程更简单且参数控制更少，更有利于复杂环境下的快速控制。

(8)

Li(k)=2α|c(k)-xi(k)|

(9)

Pi(k)=φi(k)pi(k)+[1-φi(k)]g(k)

(10)

xi(k+1)=Pi(k)±Li(k)/2·ln[1/ui(k)]

(11)

式中：k为当前迭代次数；M为粒子种群规模；xi(k)为第i个粒子的当前位置；pi(k)和g(k)分别表示粒子个体最优和种群全局最优位置；c(k)为第k代粒子群的平均最优位置；Pi(k)和Li(k)表示粒子局部吸引子位置和粒子聚集态的特征长度；ui(k)和φi(k)均为[0,1]区间上均匀分布的随机数，当ui(k)小于0.5时，式(11)取“+”号，否则为“-”号；α为扩张-收缩因子。

针对适应度函数的选取问题，因评估制导律性能的指标不唯一，本文在综合考虑导弹飞行时间和脱靶量指标基础上，以权重法将多目标优化问题转化为单目标优化问题。为了约束制导精度，针对脱靶量指标增加指数型惩罚函数，适应度函数具体形式为：

(12)

其中：wt和wd是用以调整对两个指标偏好程度的权重系数，考虑到两个指标取值范围的不同，令wd=0.02，wt=0.03；ft表示导弹的飞行时间；Md为导弹脱靶量；Rk为导弹的有效杀伤半径，取10 m；λ是惩罚因子，取0.05。

由文献[12]知，通过调整比例系数可以影响导弹的飞行时间。而在诱饵干扰环境下，导弹每一时刻状态都会对识别出目标的时机产生影响，进而影响脱靶量。同时，发射距离又正相关于导弹的飞行时间。故选取比例系数和发射距离作为搜寻最小适应度值的决策变量。

干扰样式[M,INd,vd,αm,φm]中M∈{1,2,3}对应式(5)、式(6)及式(7)的机动样式，INd表示投掷间隔，vd为诱饵投掷速度，αm及θm分别为载机发射导弹时在水平面及俯仰面内的进入角，定义正后方尾追态势的水平进入角为零，沿0°轴顺时针旋转为正方向；下视攻击时垂直进入角为负，其示意图如图2所示。

图2 进入角示意图Fig.2 Schematic diagram of the approach angle

针对上述干扰样式，搜索最优比例系数和发射距离的步骤如算法1所示。

2.2 基于RBF网络的训练方法

由于诱饵干扰情况下导弹与辐射源之间相对态势复杂，难以根据传统理论给出抗干扰制导律的解析表达式。RBF网络可逼近任意非线性函数，且结构简单、训练效率高。考虑到系统对实效性的要求，本文引入RBF网络框架对PNG的最优比例系数及导弹发射距离进行预测。

算法1 QPSO算法搜索最优调控参数步骤

本文中RBF网络由3层网络组成，结构如图3所示。

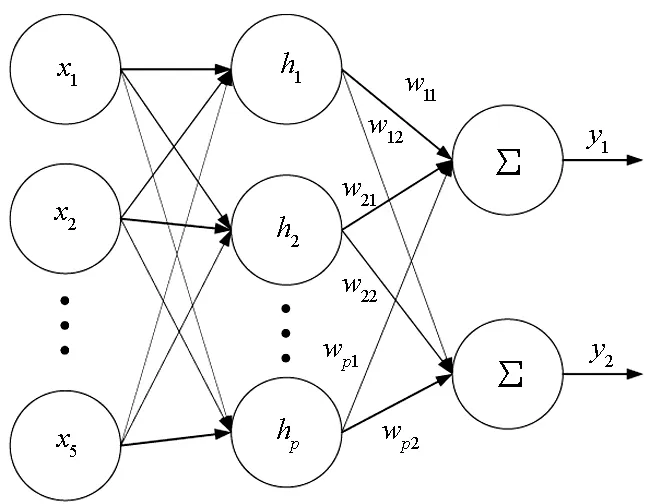
图3 RBF网络结构图Fig.3 Flow chart of RBF network

其中，x=[x1,…,x5]T为归一化输入向量，网络隐含层输出h=[h1,…,hp]T，其中p为隐含层的节点数，hj是隐含层第j个神经元的输出，表达式为：

(13)

其中

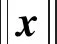
RBF网络的权值为：

RBF网络的输出y=[Kmopt,Rlopt]T为：

(14)

网络的逼近误差指标函数为：

(15)

其中，y为输出的期望值。

之后，采用带动量的梯度下降算法更新t时刻的参数向量wt、ct及bt。

(16)

(17)

(18)

式中，η为学习速率，α为动量因子。

3 RBF网络下的PNG智能调控策略

3.1 数据预处理

因输入、输入特征单位各不相同，故需先将数据进行归一化处理。同时，为保证训练数据的有效性，需对有效弹道做如下约束。

2)目标和导弹在飞行过程中应满足以下限制：

• 弹目飞行高度范围为[1 km,20 km]；

• 导弹主动段最大过载为60g，被动段最大过载40g；目标机动最大过载为9g；

• 导弹视线角速度最大为π/2 rad/s。

3.2 RBF网络初始化

为提高RBF网络训练效率，本文结合K-means与K最近邻(K Nearest Neighbors, KNN)算法对高斯核函数初始参数进行设置，流程如图4所示。

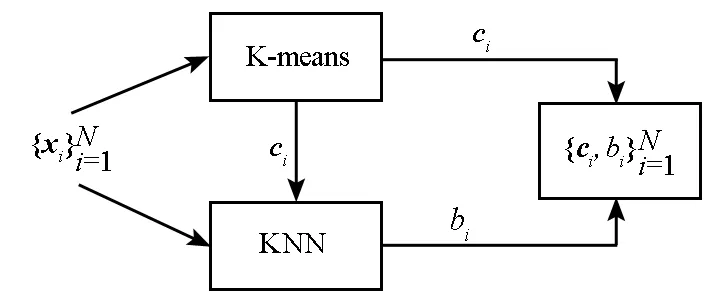
图4 高斯核函数初始参数设置流程Fig.4 Flow chart for setting Gaussian kernel function

初始化过程可分为如下两步：

1)K-means初始化中心向量。设两个数据间的欧氏距离为：

(19)

式中，xi,d表示数据xi的第d个特征值。

定义第q个高斯簇中心为Cq，其中q为小于p的整数，更新方式如下：

(20)

其中，Cq表示第q个高斯簇，|Cq|表示第q个高斯簇中数据对象的个数，Cq为含有n个特征的向量。在迭代过程中更新高斯簇及其中心，并根据如下误差函数判断是否终止。

(21)

当ΔJ<δ时，迭代终止。 此时上述所得高斯簇中心即为初始化的中心向量。

2)KNN初始化宽度。 宽度bj的初始化可利用式(20)的结果并结合KNN规则，其计算方法为

(22)

对于网络的初始权值w均为[0,1]之间的随机值。

3.3 在线输入特征获取

在线预测时需获取目标机动及诱饵干扰信息，但上述变量均需要在发射导弹之前就已确定。为了估计上述两个特征，本文基于载机平台提出如下估计方案。

1)目标机动样式估计。在目标与载机近距离格斗过程中，目标为躲避被对方雷达锁定，会投掷诱饵弹进行干扰，同时采取相应的规避机动以摆脱对方的跟踪。此时可基于交互多模型利用卡尔曼滤波方法对目标的加速度持续估计[13]，通过观测时间窗内加速度的变化值，与机动库中的机动样式进行比对以判断目标的机动方式。

2)诱饵投掷间隔估计。诱饵燃烧后会引起能量辐射强度的骤变，而该变化信息可通过红外探测器观测得到。为此，本文采用滑窗法估计诱饵投掷间隔。

(23)

利用两步滑窗法求解的投掷间隔为：

(24)

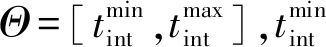
3)诱饵投掷速度估计。对于诱饵速度信息同样可通过建立红外诱饵的跟踪模型进行估计。又因诱饵在投掷后近乎做抛物线运动，故系统模型可选用简单的匀加速模型。因滤波过程中噪声的存在，本文假设诱饵投掷速度的估计误差服从均值为5 m/s，方差为50 (m/s)2的高斯分布。

3.4 RBF网络智能调控策略

RBF网络调控PNG方法的流程如图5所示。

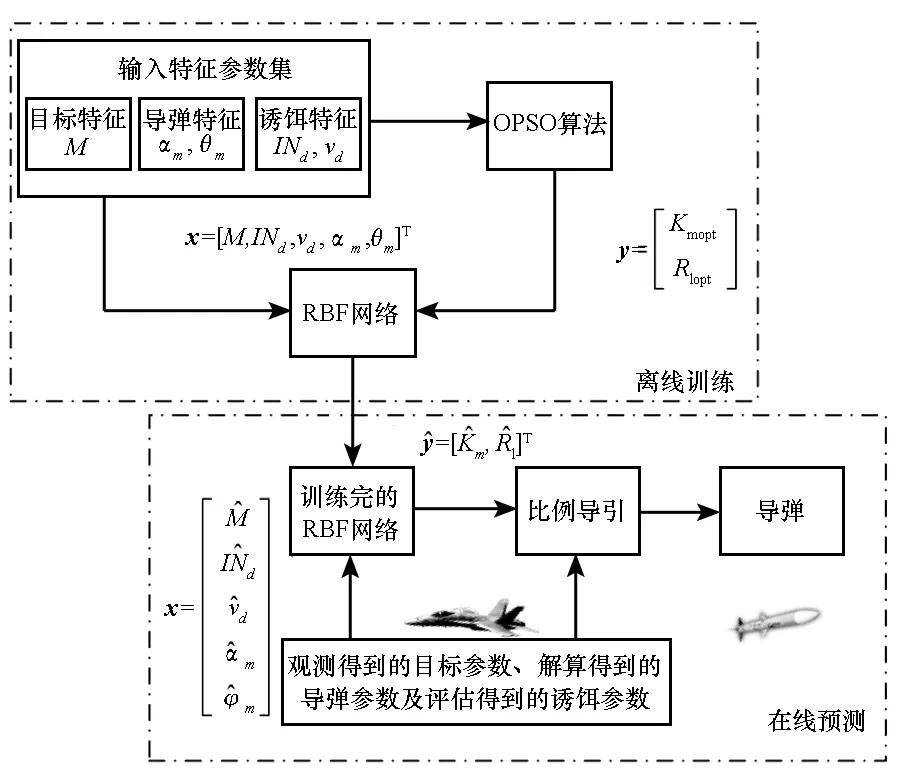
图5 RBF网络调控流程Fig.5 Regulation process of the RBF network

由图5可知，其主要分为如下两部分。

1)离线训练RBF网络。

• 获取干扰样式：针对目标的机动样式、诱饵投掷间隔、投掷速度及载机进入角进行采样并相互组合。

• 计算最优决策变量：根据式(12)，利用QPSO算法在搜索域内搜寻最优粒子，其搜索过程如表2所示。

• 数据预处理：将训练数据归一化，可选用MATLAB中的zscore函数。

• 训练网络：将训练数据输入RBF网络进行有监督训练，直至精度满足要求。

其中，为了保证训练数据的覆盖性，本文主要采用遍历变量法获得。其中目标机动样式有三种；投掷间隔范围为[0.1 s,1 s]，采样间隔0.1 s，共10种情况；诱饵投掷速度范围为[25 m/s,40 m/s]，采样间隔1 m/s，共16种情况；载机水平进入角范围为[0°,360°]，采样间隔10°，共37种情况；载机垂直进入角范围为[-90°,90°]，采样间隔5°，共37种情况。随机组合上述干扰变量则有657 120种干扰样式。然后，按照7 ∶2 ∶1比例分配到训练集、验证集和测试集进行训练。图6为RBF网络的学习曲线。

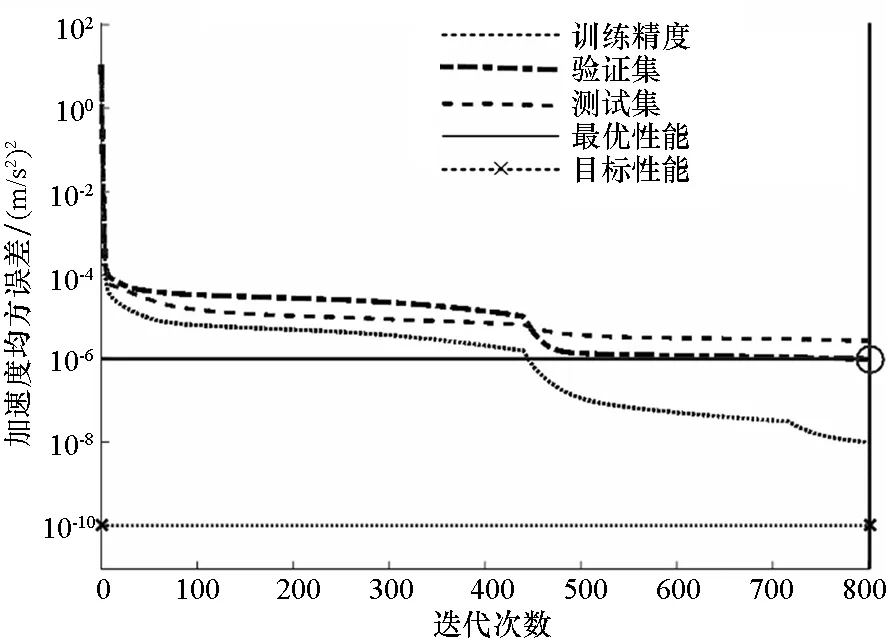
图6 学习性能曲线Fig.6 Learning performance curve

由图6知，网络在训练集上的精度可达到10-10，虽然测试集上性能稍差，但精度仍达到10-4，由此说明了该网络具有较好的泛化能力。

2)RBF网络在线预测。

• 估计当前干扰样式：按照3.3节方法估计干扰信息并实时解算载机进入角；

• 数据预处理：将原始数据转化为网络所需格式；

• 估计输出特征：输入处理后数据至训练好的RBF网络，获得预测输出值；

• 数据预处理：将输出数据转化为标准输出量。

由上述两步即可获得最优比例系数及发射时机。

4 仿真分析

分别选取两个典型对抗场景进行仿真分析，并将结果与扩展比例导引(Augmented Proportional Navigation，APN)及自适应滑膜导引律(Adaptive Slide Mode Guidance，ASMG)[14]进行比较。其中APN和ASMG导引律对应的公式分别为：

(25)

(26)

仿真初始条件：目标坐标为(30 km,5 km,6 km)，航向为(0 rad,0 rad)，初始速度为250 m/s；载机速度为400 m/s；RBF网络节点数分别为(6,200,2)。

4.1 尾后下半球攻击

该干扰样式下的参数为：目标机动样式为纵向平面急转弯机动，诱饵投掷速度为35 m/s，速度估计值分别为25 m/s、35 m/s及40 m/s，投掷间隔为1 s，载机水平进入角为π/12 rad，垂直进入角为π/60 rad。

表1为各导引律的性能对比。

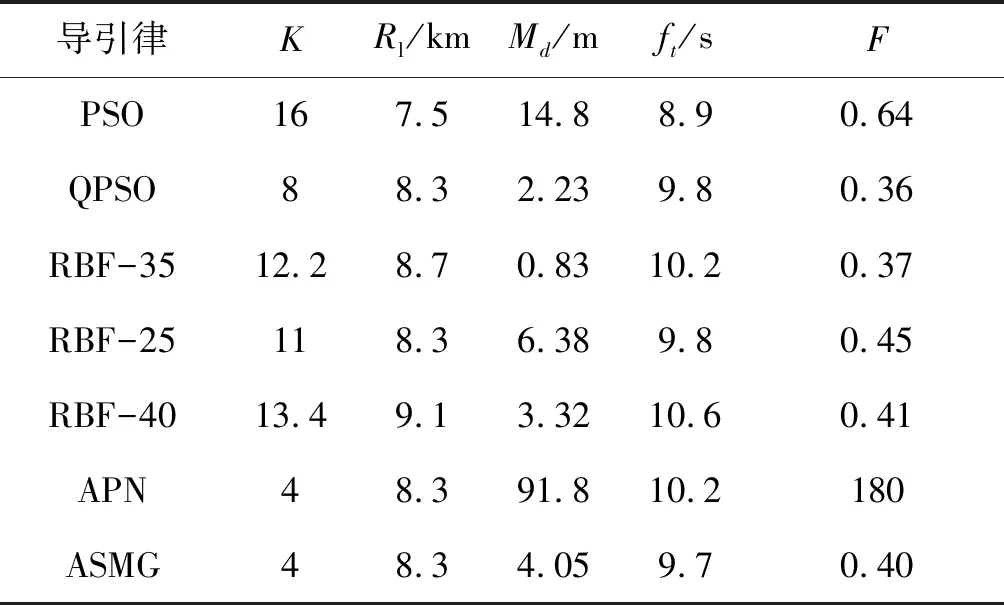
表1 尾后攻击态势下各导引律参数及性能

由表1中适应度值可以看出，QPSO及RBF网络在脱靶量指标及总体性能指标上都要优于PSO。当对投掷速度估计存在偏差时，其最终性能也与无偏差情况下性能相近，这说明该网络对于投掷速度特征并不十分敏感，也因此降低了估计误差的影响。同时，对比RBF网络与ASMG可知：当速度估计准确时，RBF网络性能要优于ASMG；当速度估计存在偏差时，其性能也近似于ASMG。

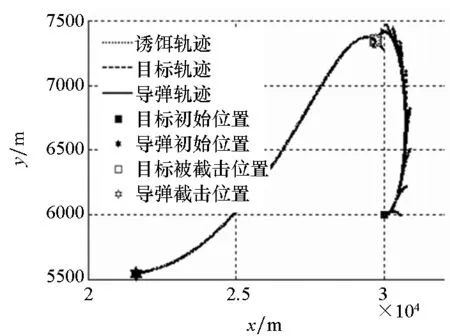
因智能寻优算法的时效性无法满足现实作战要求，下面只分析RBF网络、APN及ASMG导引律性能，其轨迹如图7所示。

图7中由于目标机动方向与诱饵投掷方向相同，导致诱饵轨迹脱离并不明显，而从寻优搜索结果中可以看出，导弹发射时的参数设置差别并不十分明显，导致各子图中导弹及目标轨迹基本重合。同时，RBF网络调控的弹道曲线与ASMG的弹道曲线最为接近，弹道都较为平缓，而APN的弹道起伏较大，易造成较大的脱靶量。

(a) RBF-35制导律轨迹(a) RBF-35 guidance law trajectory

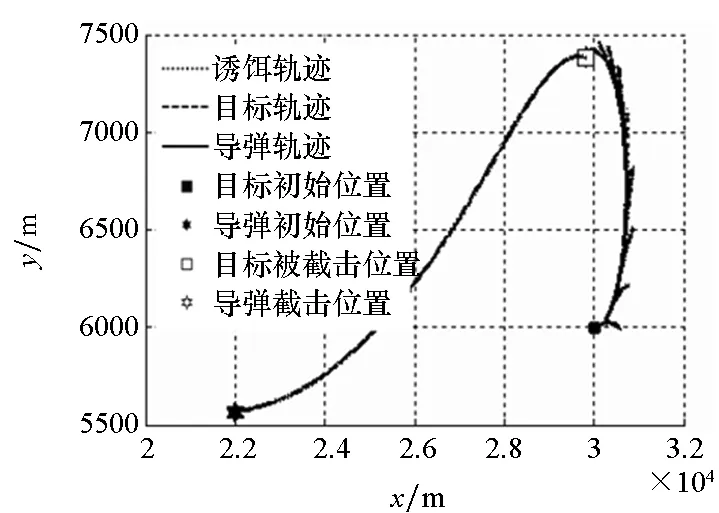
(b) RBF-25制导律轨迹(b) RBF-25 guidance law trajectory

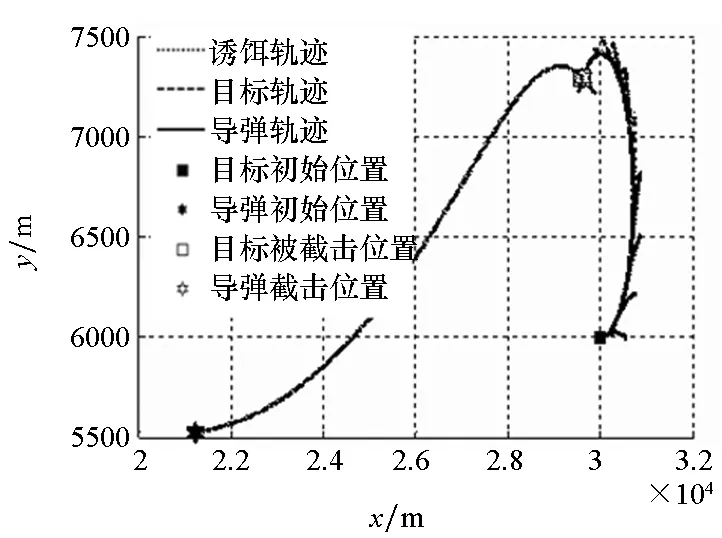
(c) RBF-40制导律轨迹(c) RBF-40 guidance law trajectory

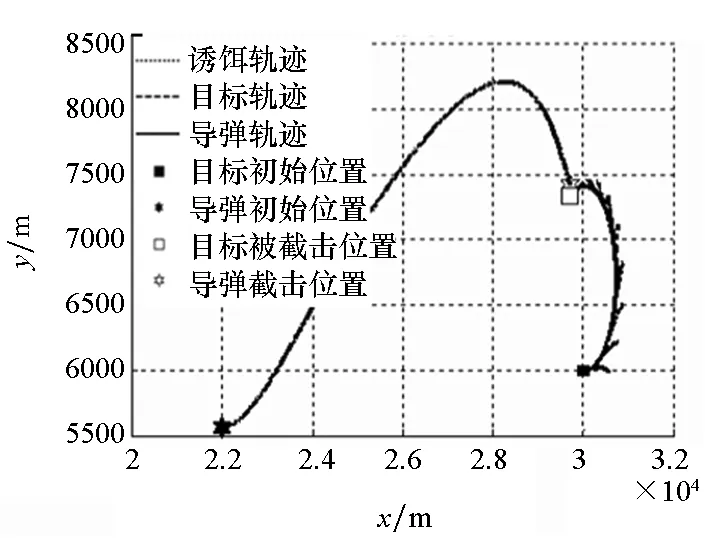
(d) APN制导律轨迹(d) APN guidance law trajectory

(e) ASMG制导律轨迹(e) ASMG guidance law trajectory图7 尾后攻击态势下的弹道轨迹Fig.7 Ballistic trajectories in the tail-on situation

采用上述导引律的过载曲线如图8所示。

图8中过载发生跳变是因为诱饵在该时刻被识别而导弹急需转向所致。其中，ASMG的过载跳变幅度最为剧烈，这不利于导引头的稳定跟踪。由图可知，投掷速度分别为35 m/s、25 m/s和40 m/s时RBF网络制导律的过载变化曲线趋势一致且较接近，打击过程中过载变化幅度较之另两种导引律要更加平缓，这非常有利于导弹节省能量进行末段打击，而APN在不断接近目标的过程中过载逐渐变大，最后甚至达到了可用过载的极限值，这非常不利于打击，由表1也可知其脱靶量最大。

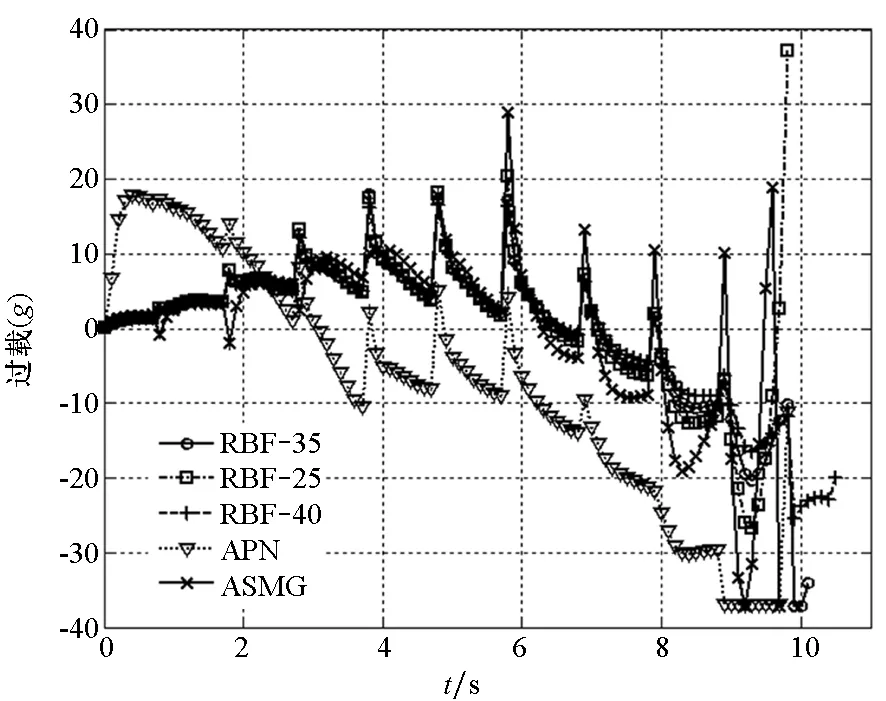
图8 尾后攻击态势下过载变化曲线Fig.8 Overload curves in the tail-on situation

4.2 迎头上半球攻击

该场景下参数设置为：载机垂直进入角为-π/60 rad，水平进入角为11π/12 rad；目标采取水平面正弦机动，诱饵投掷间隔为0.3 s，投掷速度为30 m/s，估计的速度分别为20 m/s、30 m/s、40 m/s。

该态势下的各导引律性能如表2所示。

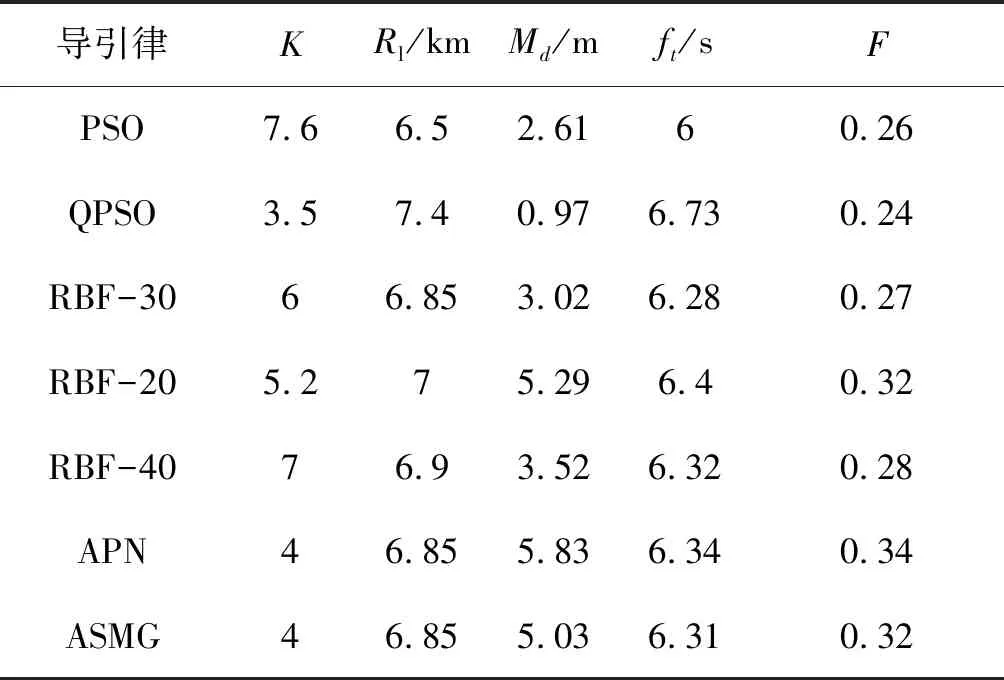
表2 迎头攻击下各导引律参数设置情况及性能

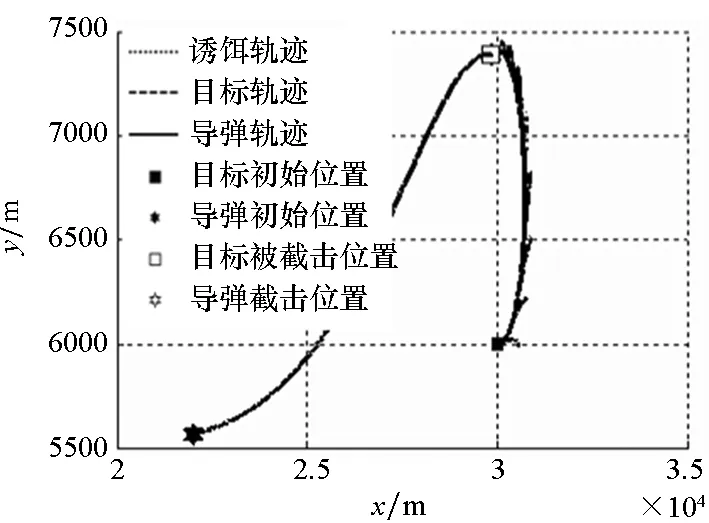
由表2可知，QPSO算法搜索到的最优决策变量获得了最小的适应度值，PSO算法的精度次之。RBF网络的性能虽然稍逊色于上述寻优算法，但在脱靶量指标及总体性能指标上都要优于APN及ASMG。对应的弹道曲线如图9所示。

图9中诱饵投掷间隔要小于图7中的场景，诱饵轨迹更加密集，并且由表2可知，各制导律下的导弹发射参数设置十分接近，这就使得各子图中导弹及目标轨迹重合度较高。同时，RBF网络与ASMG的弹道明显要比APN的平滑，这也导致APN的脱靶量在三者之中最大。

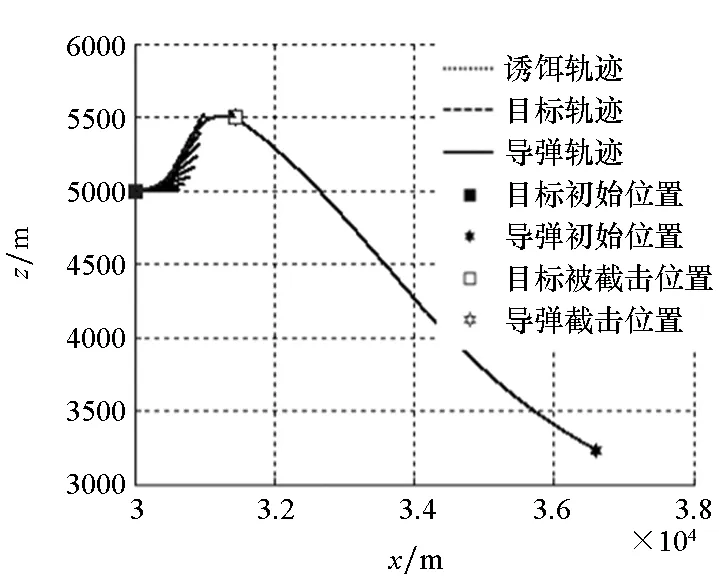
(a) RBF-30制导律轨迹(a) RBF-30 guidance law trajectory

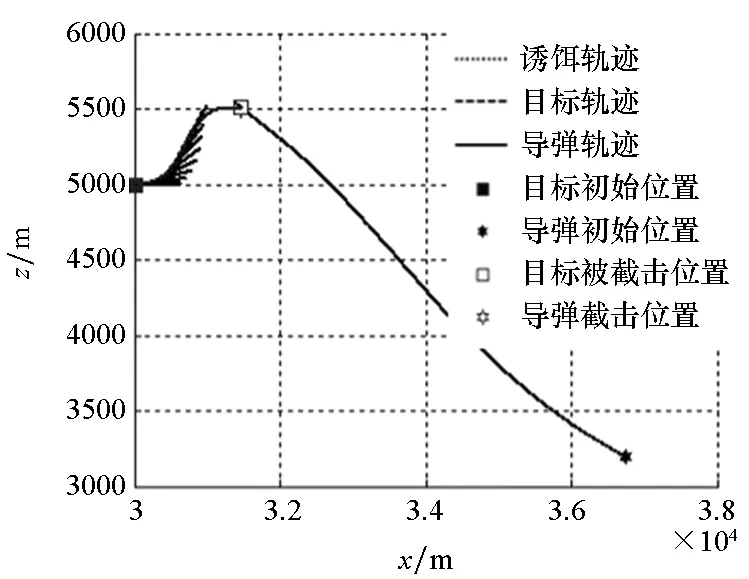
(b) RBF-20制导律轨迹(b) RBF-20 guidance law trajectory

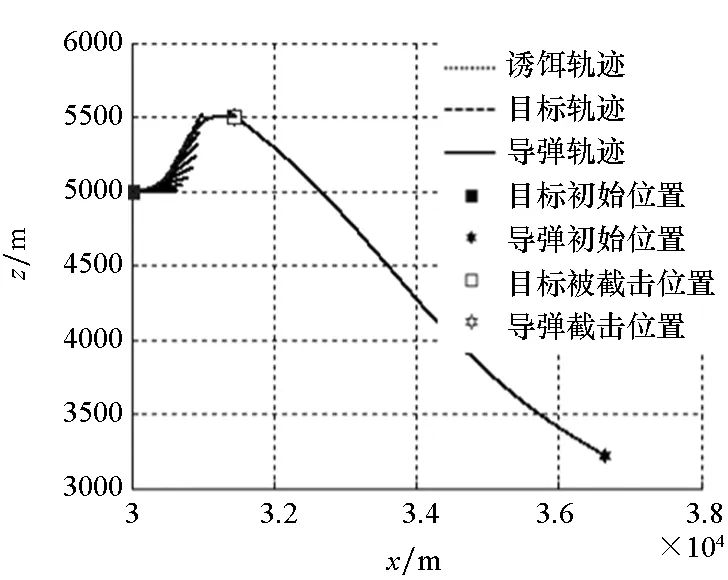
(c) RBF-40制导律轨迹(c) RBF-40 guidance law trajectory

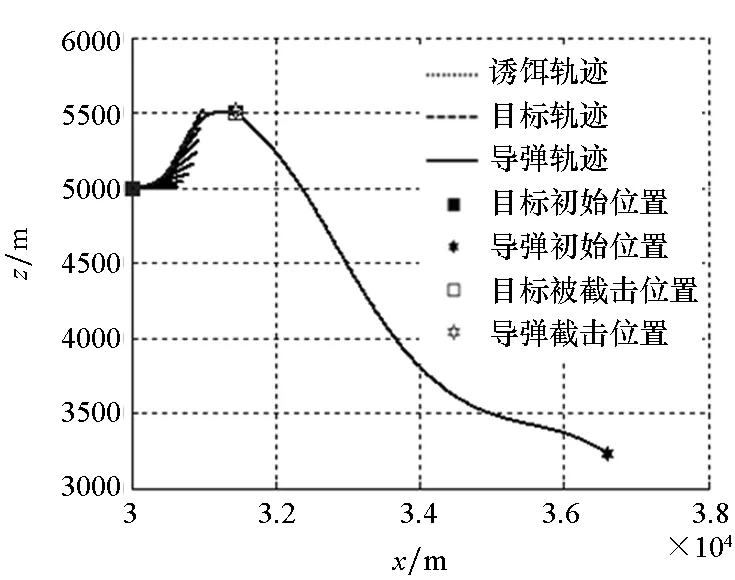
(d) APN制导律轨迹(d) APN guidance law trajectory

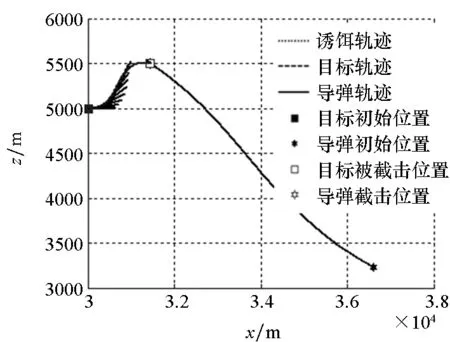
(e) ASMG制导律轨迹(e) ASMG guidance law trajectory图9 迎头攻击态势下的弹道轨迹Fig.9 Ballistic trajectories in the head-on situation

过载曲线的变化情况如图10所示。

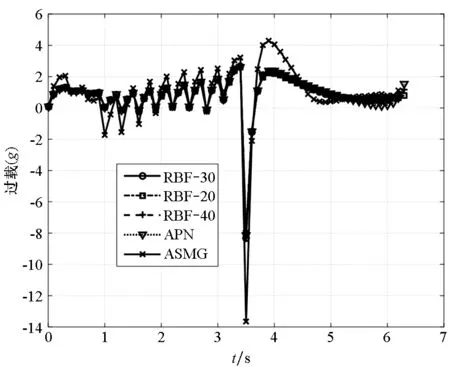
图10 迎头攻击态势下过载变化曲线Fig.10 Overload curves in the head-on situation

由图10知，ASMG过载曲线抖动得最为剧烈，而当投掷速度分别为30 m/s、20 m/s以及40 m/s，RBF网络制导律过载曲线的变化趋势十分接近且过程中起伏较小，在制导末段时过载也能够趋向较小值，这也保证了导弹的打击精度。APN的过载曲线与RBF网络的较为接近。

通过在上述典型攻击态势下对比RBF网络调控下的PN、PSO、QPSO、APN以及ASMG导引律性能，不难得出以下结论：

1)速度估计值的偏差会影响RBF网络的调控性能，使得脱靶量变大。

2)RBF网络调控方案对于投掷速度特征并不十分敏感。首先，在不同估计值下获得的最优决策变量较为接近，这也保证了当速度估计值存在偏差时总体性能仍能较好。其次，不同速度估计值下的弹道特性极为相近，但脱靶量指标仍受估计误差的影响。

3)当速度估计值不存在偏差时，RBF网络调控下的PN性能要优于ASMG；当估计值存在上述设定的偏差时，其总体性能近似于ASMG，但过载曲线更加平稳。

5 结论

仿真结果表明，基于RBF网络调控策略的PN在总体性能上不差于ASMG，且过载变化更加稳定。需要强调的是，本文所建立的RBF网络是基于文中所提的三种机动场景下，如检测出目标的机动方式不在机动库中，则可将攻击方式调整为常规的打击方式——锁定即发射导弹。这主要是由于当测试样本不在总体样本范围内时，RBF网络无法满足预测精度要求。