超图约束和改进归一化互相关方法相结合的图像配准算法
2019-06-19朱明,姚强,唐俊,张艳
朱 明,姚 强,唐 俊,张 艳
(1. 安徽大学 电子信息工程学院, 安徽 合肥 230601; 2. 偏振光成像探测技术安徽省重点实验室, 安徽 合肥 230031)
图像配准是对不同时间、不同视角、不同来源的两幅或多幅图像进行空间几何变换,使得各个图像中相同场景在几何上对准的过程。图像配准是图像处理一个重要的基础问题,是诸多应用,如目标跟踪检测、目标识别、对地观测、安全监控、智能交通、医学成像等的先决条件[1]。
图像配准方法基本上可以分为基于区域和基于特征两大类。基于区域的配准方法是直接利用像素点的灰度值来确定待配准图像之间的几何变换关系,这类方法充分利用了图像所包含的信息,不需要提取图像的特征,而是直接利用其灰度信息,因此能提高估计的精度和鲁棒性,但由于需要计算匹配点周围区域点的灰度信息,因此存在计算量大、速度较慢等问题。基于特征的配准方法是目前应用最为广泛的方法,其优点是能够将对整个图像的分析转化为对特征的分析,极大地减小了运算量,并且对灰度变化、图像变形和遮挡等都有较好的适应能力[2-6]。Pei等[7]将图像进行分割形成包含不同数量角点的局部区块,对密集角点区域进行筛选,提高了图像配准的效率和精度。Kang等[8]提出了结合互信息和角点检测的图像配准算法,该方法利用互信息作为特征点粗匹配的相似准则,然后采用随机抽样一致性(RANdom SAmple Consensus, RANSAC)算法消除误匹配进行配准。文献[9]提出了一种基于最近邻图结构的图形变换(Graph Transformation Matching, GTM)配准算法,该算法使用最近邻约束策略构造待配准特征的局部邻近结构作为特征描述方法来剔除错误匹配对,但可能会因为相同邻域结构的错误匹配点的存在,而无法完全剔除错误匹配点对。文献[10]对RANSAC算法进行了改进,提出了一种改进样本一致性(Fast Sample Consensus, FSC)配准算法,该算法利用不同均方根误差获得不同正确匹配率的样本子集,从高正确率的样本子集中得到全局变换模型剔除低正确率的样本子集中的错误匹配进行配准,它与RANSAC算法一样都过于依赖随机样本的选择。文献[11]提出了一种特征点对齐度准则,并基于该准则进行图像配准,该方法首先提取特征点的角度信息,然后计算特征点对之间的对齐度,从而得到最终的匹配对进行配准,这样不仅计算量大,而且出格点的存在会影响该方法的配准精度。
为提高图像配准的精度和配准方法的适应能力,本文提出了超图约束和改进归一化互相关方法相结合的图像配准算法。
1 初始匹配
1.1 Hessian-Affine特征
Hessian-Affine特征检测算子是Mikolajczyk等在文献[12-13]中提出和完善的。Hessian-Affine特征检测算子是基于图像上某点的Hessian矩阵进行兴趣点计算,选择在多尺度下Hessian矩阵行列式具有局部最大的兴趣点。在每个独立的尺度下,得到一系列对旋转、尺度、平移、亮度改变稳定的点,然后运用多尺度迭代算法进行空间定位和筛选尺度、仿射不变特征。该算子相对其他仿射不变算子而言,可以检测出更多特征区域且具有较高的准确性[14],因此可以有效解决图像配准中局部畸变等难题。
1.2 改进的NCC匹配算法
归一化互相关(Normalized Cross Correlation NCC)匹配方法通过比较两幅匹配图像在特征点上的归一化互相关系数来衡量匹配的程度,最大相关系数对应最佳匹配。在得到的特征点集合中,以每个特征点为中心,取一个(2N+1)×(2N+1)大小的相关窗,设参考图像I中第i个特征点和输入图像(待配准图像)J中第j个特征点对应的窗口像素的灰度值分别是I(x,y)和J(x,y),通过式(1)归一化互相关函数计算两个特征点之间的NCC值进行特征点匹配。NCC的值域为[-1,1],NCC为-1时,表示两个相关窗口不相似;NCC为1时,则表示两个窗口完全相同。
(1)
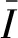
设由HNCC算法得到的I和J的s个特征点分别为v1,v2,v3,…,vs和u1,u2,u3,…,us,通过双向匹配策略可以较大程度地提高匹配正确率,但仍会存在一部分误匹配点,接下来仍需要剔除剩余错误匹配并在剩余的匹配点对中求解变换矩阵。
2 超图匹配理论
若任意一条边均连接两个以上的点,则称为超图,如果每条边均连接k(k≥3)个点,则称该超图为k一致超图。相对于一般图来说,超图能很好地描述数据点间的多维关联信息[15-16]。
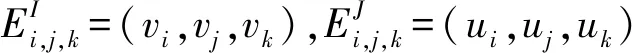
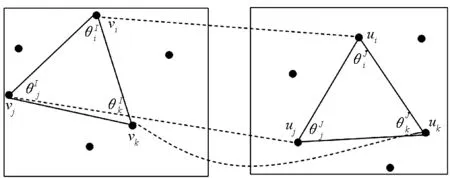
图1 相似度计算模型Fig.1 Similarity calculation model
Hi,j,k=
(2)
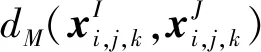
(3)
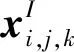
3 基于超图约束的图像配准算法
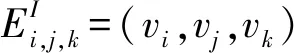
Score(t)=Score(t)+Hi,j,k,t={(vi,ui),(vj,uj),(vk,uk)}
(4)
其中,σs∈(0,1),t表示当前三角结构下的3个匹配对。
如果两对三角结构中的3个匹配对都正确,那么这两对三角结构的相似度较大,相应的各个匹配对的分数值就有较大的增幅;如果三角结构中存在错误匹配,那么得到的相似度值较小或者为0,匹配对的分数值增加较小。在比较完所有的三角结构之后,得到的正确匹配对的分数值会高于错误匹配对的分数值。
所以,根据Score(x)的值按从大到小的顺序对s对特征点对排序,得到s对匹配对集合:C={c1,c2,…,cs},其中ci=(vi,ui)为第i个匹配对,且Score(ci)≥Score(ci+1)。选取集合C中前4个特征点对初始化正确匹配对集合C′={c1,c2,c3,c4}并求解图像变换矩阵,然后逐步判断集合C中剩余的匹配点对,并更新正确匹配对集合C′和变换矩阵T,具体步骤如下:
步骤1:对参考图像I和待配准图像J中的s对特征点对,根据Score(x)值从大到小排序,得到s对匹配对集合:C={c1,c2,…,cs}。
步骤2:用集合C的前k个匹配对初始化正确匹配对集合C′,初始化k=4。
步骤3:检验集合C中第k+1个匹配对,根据正确匹配对集合C′求变换矩阵T,对集合C中在待配准图像J的第k+1个特征点做变换,得到待检验点在参考图像I上的坐标,利用均方根误差选择是否剔除此匹配点对,如果所得均方根误差小于容错误差,则加入集合C′,并更新k=k+1。
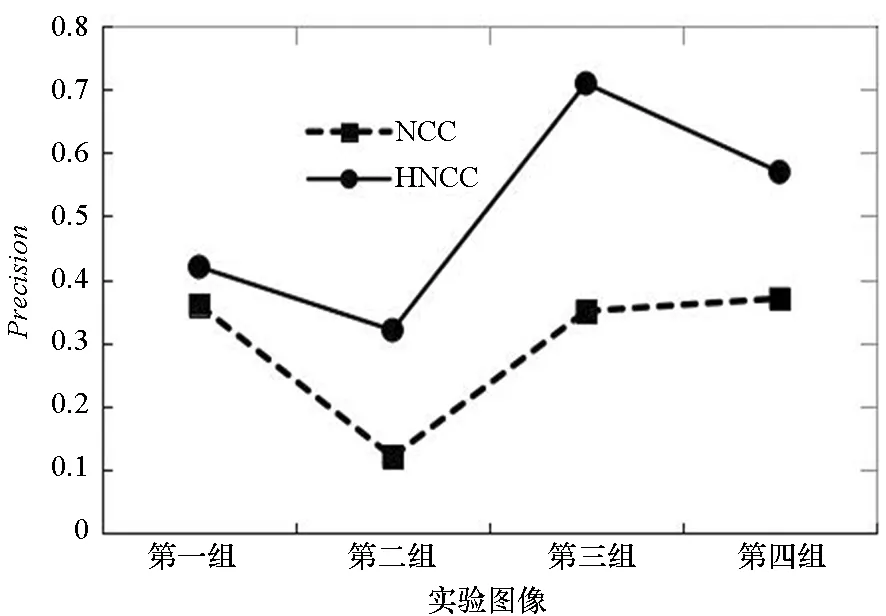
步骤4:判断是否检验完集合C中剩余的s-k个匹配对,若k 步骤5:通过双线性插值对待配准图像进行重采样,最终实现配准。 实验图像共有4组,如图2所示,左边为参考图像,右边为待配准图像,第一组图2(a)和第二组图2(b)是来自Mikolajczyk测试数据集的“wall”和“graf”,两组均为不同视角下的旋转和尺度变换图像,并且包含不同形式的重复纹理。第三组图2(c)是不同视点拍摄的同一地点的遥感图像,第四组图2(d)是两幅尺寸不同而且存在较大角度差异的遥感图像。 (a) 第一组“wall”图像(a) The first set of “wall” images (b) 第二组“graf”图像(b) The second set of “graf” images (c) 第三组遥感图像(c) The third set of remote sensing image (d) 第四组遥感图像(d) The fourth set of remote sensing image图2 实验图像Fig.2 Experimental images 在初始匹配中,NCC归一化互相关匹配和改进得到的HNCC匹配方法在四组实验图像上的匹配效果用Precision作为评价指标。该指标直观反映出匹配方法的有效性,Precision定义如下: Precision=Nc/(Nc+Nf) (5) 其中,Nc是指正确匹配对的数目,Nf是指错误匹配对的数目。Precision值越大,则匹配效果越好。 在四组图像提取的特征点中,随机选择部分特征点作为NCC与HNCC算法的匹配特征点,两种方法关于Precision的实验对比结果如图3所示。 图3 NCC和HNCC算法关于Precision的性能对比Fig.3 Comparison of NCC and HNCC algorithms on precision performance 配准算法的一个性能评价指标采用均方根误差(Root Mean Square Error, RMSE),其值越小表明配准效果越好。均方根误差是各个误差平方和的平均值的开方,计算公式为: (6) 对图像配准精度的另一个指标采用归一化互信息(Normalized Messure of mutual Information, NMI),它是一个重要的全局指标,由Studholme等[17]提出,其值越大则表明图像配准的效果越好,其中NMI的最大值为2。 为了验证文中配准算法的有效性,使用图3中HNCC算法的匹配结果作为初始匹配的输出,将本文配准算法与RANSAC算法剔除误匹配算法、GTM算法、FSC算法进行比较,其中对于求解图像变换矩阵的方法均采用最小二乘法,变换模型选择射影变换(projection transform)模型。上述几种算法重复100次在均方根误差上的平均值取得的对比结果和在NMI上的平均值对比结果如表1所示。 由图3知,改进得到的HNCC算法在四组图像中的匹配准确率均高于NCC方法,因此HNCC算法匹配性能最好。由表1可知,在相同的初始匹配情况下,本文算法能够在几种算法的对比中取得最低的均方根误差和最高的NMI值。在实验中,虽然HNCC算法极大地提高了初始匹配正确率,但由于在初始匹配中使用的特征点是从提取的特征点集合中随机选取一部分得到的,所以在各组图像上得到的初始匹配对中错误匹配所占的比例会比较高,尤其是在第二组实验图像中,图像形变较大,正确匹配对所占的比例非常低,正确率仅为0.32。在这种情况下,RANSAC、GTM和FSC方法配准失败,而本文算法不仅能成功配准,而且效果较好。实验中导致配准失败的原因是无法全部剔除错误的匹配,而本文算法则可以完全剔除错误的匹配。图4为四组图像在本文算法下的匹配和配准结果。 表1 几种算法配准精度对比 注:“-”代表配准失败。 (a) 第一组图像匹配及配准结果(a) Results of matching and registration results of the first set of image (b) 第二组图像匹配及配准结果(b) Results of matching and registration results of the second set of image (c) 第三组图像匹配及配准结果(c) Results of matching and registration results of the third set of image (d) 第四组图像匹配及配准结果(d) Results of matching and registration results of the fourth set of image图4 本文算法在实验图像上的匹配和配准结果Fig.4 Results of matching and registration of the algorithm in the experimental image 针对各场景中的图像配准问题,提出了超图约束和改进归一化互相关方法相结合的HNCC算法。实验结果表明,HNCC算法有较好的匹配效果,配准方法具有较高的配准精度和适应能力,且对于形变较大的图像也有很好的配准效果。4 实验及结果分析




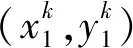




5 结论
