基于系统动力学的物流服务供应链信息共享模型构建

周娴娴 赵宏霞

中图分类号：F252   文献标识码：A

内容摘要：传统供应链上企业物流业务外包产生的第三方物流、第四方物流促进了物流服务供应链的形成。已有研究表明，物流服务供应链上亦存在牛鞭效应，文章在此基础上研究了信息共享对物流服务供应链牛鞭效应的协调作用，并运用系统动力学的方法分别构建了物流服务供应链基准模型和信息共享模型，并对其进行了仿真对比分析。结果表明，信息共享模型下物流服务供应链上牛鞭效应得到有效缓解。

关键词：物流服务供应链   信息共享   牛鞭效应   系统动力学

引言及文献综述

我国发展已进入“十三五”中后期，服务业已跃居成为国民经济第一大产业，服务业成为了我国经济增长的新引擎。由此，学术界逐渐将目光转向服务供应链。物流服务供应链作为服务供应链中的典型，受到学者们的极大关注。Goran Persson（2001）和Heigeviru從物流服务的复杂性和资产专用性角度，将物流服务商分为物流服务集成商、先进的物流网络商、专业化物流服务商和基本物流服务操作商;田宇（2002）建立了较为完善的物流服务供应链结构模式，即以集成商和供应商、集成商和制造企业为主体的链式结构;崔爱平（2009）等首次为物流服务供应链做出了较为详尽的定义;宋志刚（2015）等提出，应重视客户在物流服务供应链中的地位和作用，要将物流服务供应链的研究视角从保障能力供应向满足客户需求转变;Don Won Cho（2012）等构建了衡量服务供应链管理绩效的框架体系;赵海峰（2017）等考虑采购资金约束条件下针对三种采购方式的物流服务能力的采购决策，并构建了采购模型;桂寿平（2010）等指出，物流服务供应链中存在牛鞭效应，且处于下游的集成商通过契约的形式将需求变动的危机转嫁给上游的功能型物流服务供应商。

系统动力学自创立以来，在半个多世纪内得到广泛传播，现已在宏观领域、项目管理领域、学习型组织领域、物流与供应链领域、公司战略领域等广泛应用。Wangphanich，Pilada（2007）建立了多产品、利用多级供应链的系统动力学模型;Li，Xu（2009）等通过建立不同等级的供应链模型，分析得出引起牛鞭效应的主要原因是可控的信息延迟和订货周期;于晓霖（2007）等构建了基于APIOBPCS采购模式和VMI的七成员供应链模型，并通过该模型研究了平滑指数、库存初始值等8个因素对牛鞭效应的影响。但上述研究大都基于产品供应链的角度研究牛鞭效应，对服务供应链上牛鞭效应的研究涉及较少。本文基于物流服务供应链的角度，运用系统动力学的方法构建了信息共享模型，以此研究物流服务供应链上牛鞭效应的协调问题，并运用Vensim PLE软件对模型进行仿真分析。

问题描述与基本假设

本文主要研究信息共享对功能型物流服务提供商（FLSP）、物流服务集成商（LSI）及企业客户组成的二级物流服务供应链（LSSC）中牛鞭效应的协调问题，其结构如图1所示。假设LSSC上只存在唯一的FLSP和唯一的LSI，并只考虑运输这一单一物流服务能力，且该LSI物流服务能力的市场占有率为30%。本文以系统动力学方法分别构建LSSC基准模型和LSSC信息共享模型，并进行仿真分析。

为方便研究，本文对模型做出做如下假设：H1：LSI面临的市场价格稳定，其需求在一定范围内随机波动;H2：LSI的所有物流服务能力均来自向FLSP采购，且采购价格一定，即不考虑不同采购方式下的不同采购价格对LSI需求的影响。

系统动力学模型的构建

（一）物流服务供应链基准模型

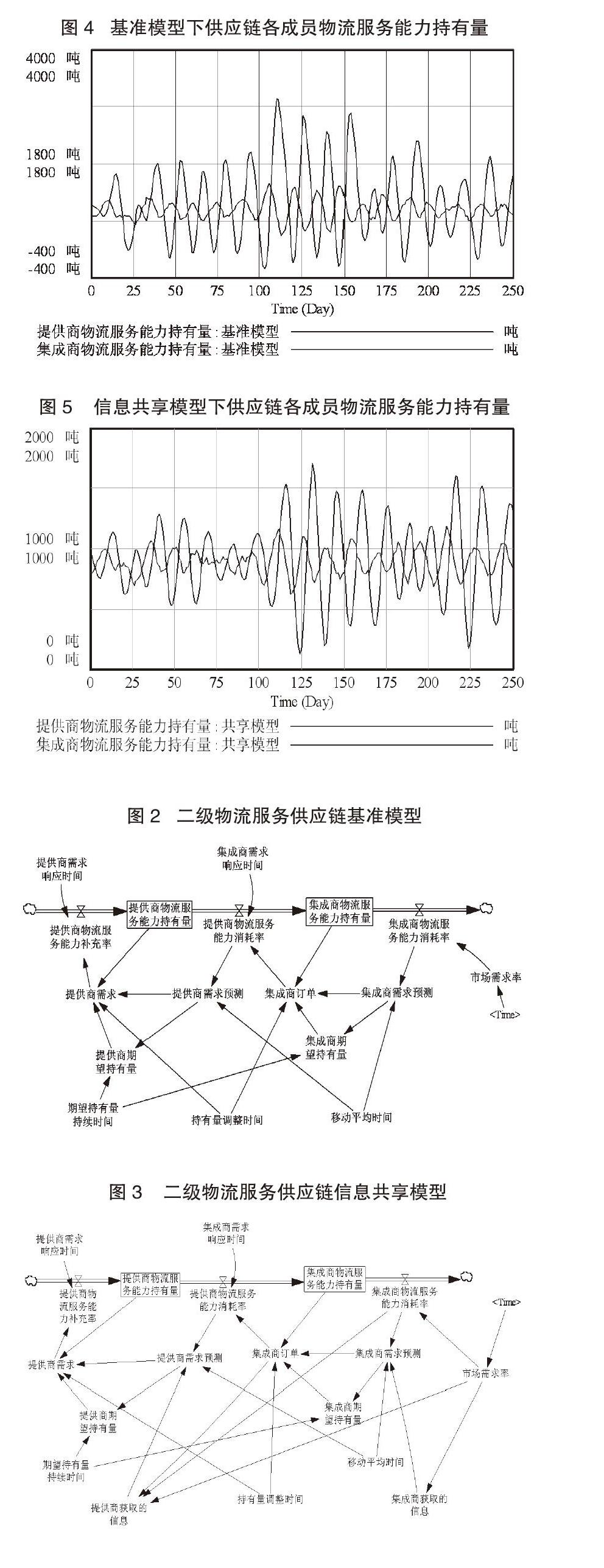
如图2所示，物流服务供应链基准模型中，FLSP子系统和LSI子系统各内部变量之间及二子系统之间变量存在复杂的因果关系链，本文通过系统动力学方程将其量化。提供商物流服务能力持有量为其物流服务能力补充率和物流服务能力消耗率的差额积累量。提供商的服务能力消耗率由集成商订单和集成商需求响应时间决定，且为FLSP提供需求预测，FLSP依据提供商需求预测、提供商期望持有量及提供商物流服务能力持有量等因素确定其需求量，进一步由提供商需求和提供商需求响应时间做出补货决策。集成商子系统有此类似因果反馈关系。不同的是，LSI面临的市场需求率在一定范围内随机波动，而集成商物流服务能力消耗率由市场需求率决定，大约占其30%。

（二）物流服务供应链信息共享模型

如图3所示，以LSSC基准模型为基础引入信息共享机制后，其提供商需求预测不再仅依赖于自身的物流服务能力消耗率，还可依据信息共享捕获的市场需求率及集成商需求率（通过集成商订单体现）知识做出更加精准的需求预测。与此同时，FLSP调整其期望持有量及订货决策，避免资源浪费或短缺。在LSI子系统中，集成商需求预测、集成商期望持有量及集成商订单均在原有基础上，依据集成商获取的市场需求率信息进行调整，做出更合理的订货决策。

参数设置及方程式说明

（一）基准模型下的方程式

市场需求率= 1000+IF THEN ELSE（Time>4， RANDOM NORMAL（-200，200，0，50，4），0）;表示市场从第5周开始，市场需求率在1000的基础上随机增加或减少，其增减幅度最大值为200，均值为0，标准差为50，初始设定的随机数为4。集成商物流服务能力消耗率= 0.3*市场需求率+RANDOM NORMAL（-50，50，0，20，2）;表示集成商物流服务能力消耗率在市场需求率的30%上下随机浮动，其增减幅度最大值为50，均值为0，标准差为20，初始设定的随机数为2。集成商需求预测=SMOOTH（集成商物流服务能力消耗率，移动平均时间）;即集成商根据自身物流服务能力消耗率采用移动平均的方法进行需求预测。集成商期望持有量=期望持有量持续时间*集成商需求预测。集成商物流服务能力持有量=INTEG（提供商物流服务能力消耗率-市场需求率，800）;表示集成商物流服务能力持有量为提供商物流服务能力消耗率与市场需求率之差的积累量，其中初始值为800。集成商订单= MAX（0，集成商需求预测+（集成商期望持有量-集成商物流服务能力持有量）/持有量调整时间）;表示集成商的订单由集成商需求预测、集成商期望持有量、集成商物流服务能力持有量及持有量调整时间决定，且当后段式值小于0时，集成商订货量为0。提供商物流服务能力消耗率=DELAY3（集成商订单，集成商需求响应时间）。提供商阶段方程式与集成商阶段相类似。

（二）方程式与参数设定

在此只列出与基准模型中相区别的部分：集成商获取的信息=0.3*市场需求率;集成商需求预测=SMOOTH（0.1*集成商物流服务能力消耗率+0.9*集成商获取的信息，移动平均时间）;表示集成商需求根据集成商物流服务能力消耗率、集成商获取的信息，采用移动平均法进行预测，其中集成商物流服务能力消耗率、集成商获取的信息二者权重为1：9;提供商获取的信息=0.5*（0.3*市场需求率）+0.3*集成商物流服务能力消耗率+0.2*集成商订单;表示提供商获取的信息由集成商的市场占有率、集成商物流服务能力消耗率和集成商订单决定，且其权重比为5：3：2;提供商需求预测=SMOOTH（0.1*提供商物流服务能力消耗率+0.9*提供商获取的信息，移动平均时间）;提供商阶段方程式与集成商阶段相类似。参数设定如表1所示。

模型仿真及分析

（一）牛鞭效应对比分析

对比图4、5可知，信息共享能有效缓解物流服务供应链中的牛鞭效应。从图4可看出，在基准模型中，提供商物流服务能力持有量波动幅度大，其最高逾2900吨，最低约至-300吨（服务能力短缺），且超过2000吨达5次之多，其牛鞭效应明显;而在信息共享模型中（如图5所示），提供商物流服务能力持有量波动幅度明显减小，其振幅最高在1500吨左右，且提供商服务能力持有量均在2000吨以下，提供商和集成商均不出现服务能力短缺情况，牛鞭效应显著改善。

（二）物流服务能力持有量对比分析

由图6、图7可以看出，在信息共享模型下，提供商和集成商的物流服务能力持有量均值均小于基准模型下二者的持有量。其中，提供商物流服务能力持有量在信息共享后波动幅度大为下降，波动周期略微延长;相较于提供商，集成商物流服务能力持有量在信息共享后波幅变化程度小，但可看出在原有基础上明显下降，波动周期略微延长

结论

传统的物流服务供应链上存在严重的牛鞭效应，但随着信息共享机制的加入，提供商和集成商的物流服务能力持有量均显著下降，供应链各成员需求更加稳定，牛鞭效应明显减弱。

信息共享机制有效地缓解了物流服务供应链中的牛鞭效应，即使在采用期权契约采购时，处于供应链上游的提供商也不再承担过高的需求变动危机，从而有利于供应链整体效益最大化。此外，本文基于系统动力学的物流服务供应链牛鞭效应协调研究，可为物流服务供应链的实践与运作提供一定的理论依据。

参考文献：

1.田宇.物流服务供应链构建中的供应商选择研究[J].物流技术，2002，23（4）

2.崔爱平， 刘伟.物流服务供应链中基于期权契约的能力协调[J].中国管理科学，2009，17（2）

3.宋志刚，赵启兰.物流服务供应链的研究——从供应到需求的视角转变[J].商业经济与管理，2015（3）

4.赵海峰，何青，Edison.考虑采购资金约束的物流服务能力采購决策[J].管理科学学报，2017， 20（5）

5.桂寿平，丁郭音，张智勇等.基于Anylogic的物流服务供应链牛鞭效应仿真分析[J].计算机应用研究，2010，27（1）

6.于晓霖，刘敬保.基于APIOBPCS模式VMI下牛鞭效应仿真研究[J].管理科学，2007，20（6）