Nonlocal effect on resonant radiation force exerted on semiconductor coupled quantum well nanostructures∗

Jin-Ke Zhang(张金珂),Ting-Ting Zhang(张婷婷),Yu-Liang Zhang(张玉亮),Guang-Hui Wang(王光辉),†,and Dong-Mei Deng(邓冬梅)

1Guangzhou Key Laboratory for Special Fiber Photonic Devices,South China Normal University,Guangzhou 510006,China

2Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices,South China Normal University,Guangzhou 510006,China

Keywords:nonlocal effect,resonant radiation force,coupled quantum well

1.Introduction

Utilizing optical force to alter the motion of micrometresized particles[1]and neutral atoms[2]could have potential applications in the manipulation of microscopic particles and of individual atom.Therefore,the optical force and optical manipulationof nano-objects have been attracting extensive interestsand have been successfully applied in various fields such as plasmonic nanoparticles,quantum dots,biology,etc.[3-11]For example,Nieto-Vesperinas et al.[5]had announced the study of the optical force on a small particle with both electric and magnetic response,and clari fied the origin and signi ficance of the electric-magnetic dipolar interaction force,which is related with the angular distribution of the extinction cross section and of scattered light.

Recently,the nonlocal optical effects in semiconductor and metal nanostructures have been drawing more and more attention.[12-20]The so-called nonlocal optical response is that the polarization at a spatial point is induced by the applied optical fields not only at the same point,but also at other positions within the extent of the relevant wave function of electrons.Therefore,when we take the nonlocal optical response into account,susceptibility tensors and dielectric permittivity would be more complex.These pioneering works of spatial nonlocality in semiconductor materials have developed into two successful research aspects:nanostructures[21]and metamaterials.[22]For instance,Mortensen[23]had found some important nonlocal effects in metamaterials and Batke et al.[24]demonstrated a strong nonlocal interaction of twodimensional(2D)magnetoplasmon resonance with harmonics of the cyclotron resonance in AlGaAs/GaAs heterostructures.Moreover,there are also a great deal of interests in nonlocal optical effects for mesoscopic systems,resulting in the development of nonlocal theory and nonlocal optical properties in plasmon and semiconductor nanostructures.[25-28]The nonlocal optical response of metal nanostructures with arbitrary shape had been investigated and the particular importance of nonlocal effects in apex structures had been indicated by McMahon et al.[20]Furthermore,Kosionis et al.[29]had also taken nonlocal effects into consideration in the research on optical effects in quantum-dot/metal-nanoparticle hybrid systems.As far as we know,the spatial nonlocal effects on optical force have not been clari fied.It is reasonable to believe that the spatial nonlocal effects may have an important influence on the optical force exerted on nanodevices.The physical motive of our paper is to demonstrate and explain the optical force exerted on a coupled semiconductor quantum well nanostructure(CQWN)from the resonant intersubband transitions for two different polarized states under spatial nonlocal effects.

This paper is organized as follows.In Section 2,a basic theoretical framework for optical force applied on a CQWN with two kinds of polarized states is presented by taking the spatial nonlocality of optical response into account.Section 3 is dedicated to the results and discussions for AlGaAs/GaAs CQWN.And finally,our conclusions are given in Section 4.

2.Theoretical framework for optical force on a CQWN with nonlocal response

In what follows,let us consider that a monochromatic plane wave with an incident angle θ and an angular frequency ω in the cases of p-and s-polarized states,is incident on a CQWN con fined in the z direction,as shown in Fig.1.In general,the Lorentz force acting on an object induced by an electromagnetic field is described as[30]

where EEE ( rrr ,t)and BBB( rrr,t)are the electric and magnetic fields,respectively.ρ( rrr,t)is the charge density,and jjj( rrr,t)is the current density.V is the volume of the force body.The charge density can be written as ρ( rrr ,t)=-∇· PPP( rrr ,t),where PPP( rrr,t)is the induced polarization intensity.

Fig.1.(a)The schematic diagrams of radiation forces acting on a CQWN con fined in the z direction,where Fxand Fzdenote the x and z components of the radiation force induced by a monochromatic plane wave with p-or s-polarized state,respectively.(b)The schematic diagrams of the CQWN,where LL,LB,and LRdenote the left well,mid-barrier,and right well widths,V1and V2denote the mid-barrier and outer barrier height,respectively.The signs↑and⊙denote polarization direction of p-and s-polarized light waves,respectively.

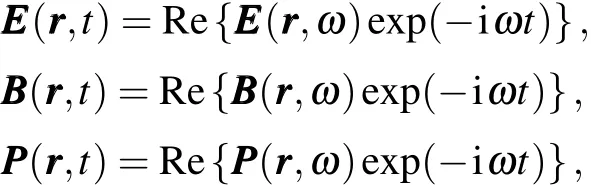
For time-harmonic electromagnetic fields,we have where EEE ( rrr ,ω), BBB( rrr ,ω),and PPP( rrr,ω)are complex functions of position and frequency.Re denotes the real part.The timeaveraged force in the case of time-harmonic electromagnetic fields is derived as[8]

where∗denotes the complex conjugate.Under the nonlocal linear response,the resonant part of the induced polarization is described as

In the following,let us consider the AlGaAs/GaAs CQWN restricted in the z direction,as shown in Fig.1.Based on the effective mass approximation,the Schr¨odinger equation for electrons in CQWN can be written as

with the confinement potentialV(z)

where z represents the confinement direction of the CQWN;V1and V2denote the mid-barrier and outer barrier height,respectively;h¯ is Planck constant;m∗is the effective mass of an electron in the conduction band;En,qand ψn,q( rrr )denote the eigenenergies and eigenfunctions of the CQWN system,respectively.Due to the translational invariance in the xy plane and the confinement in the z direction of the system,ψn,q( rrr)and En,qcan be written as and

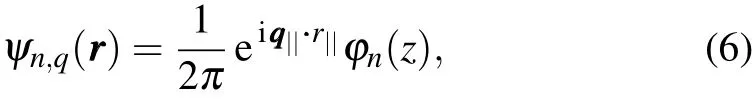
here, qqq||and rrr||are electronic wave vector and position vector in the xy plane. The solutions of onedimensional Schro¨dinger equation H0φn(z)=εnφn(z),with H0=-(h¯2/2m∗)(d2/dz2)+V(z),are φn(z)and εn,which are named the envelope wave functions and the corresponding transverse energies of the n-th subband,respectively.

For the finite-depth CQWN,the transverse energy eigenvalue εnand the corresponding electronic envelope wave function φn(z)in the CQWN can be expressed as

By substituting Eq.(3)into Maxwell’s equations,we can derive the integral-differential equation for the self-consistent complex electric field EEE ( rrr,ω)under the nonlocal linear optical response,[15]viz.

在美妆市场竞争日益激烈的今天，本土品牌一边要面对消费者的严格要求，一边要面临着进口品牌的冲击，另外一边还要寻求新的发展空间，这个时候，跨界合作无疑成为了本土品牌的一个保护伞。跨界合作能够为双方品牌都带来曝光度、知名度，同时引入精准的流量，这也是国产品牌在面对外资品牌冲击之下的自救之路，而未来，相信国产品牌会发展的更好，能够在美妆市场占据一片江山！

where the tensorial operator

Here c is the speed of light in vacuum.enotes the unit tensor.ˆexandˆezdenote unit vectors in the x and z directions,respectively. εB(ω)is the relative dielectric constant of the background medium.By the one-body density matrix method,[15]the components of the linear polarization,z,ω),for the two-level CQWN model can be obtained in the low-temperature(T→0)and long wavelength approximation(kx→0)limits as follows:

where

and Ψ(z)= φ1(z)φ2(z); ζ(z)= φ1(z)dφ2(z)/dzφ2(z)dφ1(z)/dz,ε21= ε2-ε1;e is the electron charge;Γ is the off-diagonal relaxation rate;εF=ε1+πNs¯h2/m∗is the Fermi energy of the CQWN system,where Nsis the donor surface concentration.

By the Green’s function method,[15,21]one can solve the components of the microscopic electric fieldfor spolarized state,andfor p-polarized state)from Eq.(9)as follows:

where sgn(z)is the usual sign function.

where

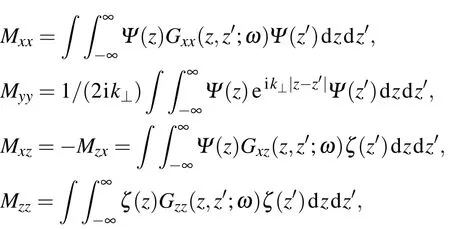
Note that,for the following analyses,equations(16)-(18)can be written in vectorial form by the rotating wave approximation[21]

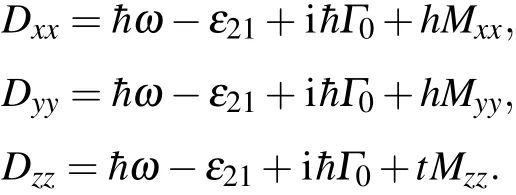
However,if we only take local optical response into account,the complex electric field EEE ( rrr,ω)and polarization PPP( rrr,ω)can be written as

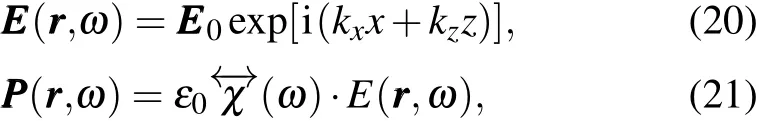
where kxand kzstand for the wave number in the x and z direction in the CQWN,respectively;(ω)is the local linear susceptibility tensor,whose elements χxx(ω)= χyy(ω)=0,χzz(ω)=Re2m∗(εF-ε1)|µ21|2/[πε0Lh¯2(h¯ω-ε21+ih¯Γ0)],hereµ21=-∞∞φ2∗(z)zφ1(z)dz and L is the total width of the CQWN.

By substituting Eq.(20)and Eq.(21)into Eq.(2),we can obtain the numerical solution of the resonant radiation force exerted on the CQWN in the case of the local optical response.

3.Results and discussion

To discuss the optical force exerted on the CQWN,we take the spatial nonlocality of optical response into account in detail.Some parameters used in the following calculation are adopted as:[12,14]m∗=0.067m0(m0is the mass of a free electron),Ns=1011cm-2,εb=13.1,and the mid-barrier width LB=1 nm.The incident intensity is assumed to be 0.05 W/cm2.

In Section 2,based on Eqs.(10)-(14),we can solve the components of the microscopic electric field EEE(z;ω)and induced polarization PPP(z;ω)by the Green’s function method[15,21]and one-body density matrix method,[15]respectively.Substituting these components into Eq.(2),we can obtainthe numerical solution of the resonant radiation force,then analyze the resonant radiation force spectra.

Fig.2.Resonant radiation force spectra(Fxdashed lines;Fzsolid lines)in the two cases of p-and s-polarization for two different width ratios:LR/LL=2.5/5(black lines),LR/LL=7.5/5(red lines)[panels(a)and(b)],and for the three different CQWN widths:LR=LL=3 nm(black lines),LR=LL=5 nm(red lines),and LR=LL=7 nm(blue lines)[panels(c)and(d)].The mid-barrier width LB=1 nm,and the barrier height V1=V2=2.0 meV,¯hΓ0=4.7 meV.

In Figs.2(a)and 2(b),the resonant radiation force is shown as a function of the normalized photon energy¯hω/ε21for asymmetric CQWN of two different width ratios between the right well width LRand the left well width LL:LR/LL=2.5/5(black line),LR/LL=7.5/5(red line)with the left well width LL=5 nm in two cases:(a)p-polarization and(b)s-polarization with the incident angle θ =45°,and the barrier height V1=V2=2.0 meV.For the sake of contrast,we also plot the resonant radiation force of the symmetric CQWN for three different widths:LR=LL=3 nm(black lines),LR=LL=5 nm(red lines),and LR=LL=7 nm(blue lines)with the same condition in Figs.2(c)and 2(d).Fxand Fzdenote the x and z components of the radiation force,respectively,where Fxhas been ampli fied three times so as to contrast with Fz.From Fig.2,one can find easily some important properties of resonant radiation force spectra:(i)The resonance peak does not occur at¯hω/ε21=1,whereas it has a deviation relative to the energy separation ε21more or less,namely,the resonance peak position occurs at¯hω/ε21=1+Δ,where Δ is called a radiation shift,which is attributed to the nonlocal optical response in the CQWN system.The magnitude of the radiation shift is dependent on the structure parameters and symmetry of the CQWN.When the CQWN is asymmetric,the radiation shift is not evident,that is,the position of the resonance peak of radiation force occurs at¯hω/ε21≈1,as shown in Figs.2(a)and 2(b).When the CQWN is symmetric,however,the radiation shift is evident,and the wider the symmetric CQWN is,the larger the radiation shift will be,as shown in Figs.2(c)and 2(d).It is because that,compared with asymmetric CQWN,the wave functions of symmetric CQWN would be broadened more due to stronger coupling effects between two wells of symmetric CQWN,which leads the characteristic response scale of electrons to increase.(ii)Fzis evidently larger than Fxin the same polarized state.This is because the quantum-size effect plays an important role in the z direction,which induces the increase of the intensity of electric polarization,due to the charged particles are con fined in the z direction of the system.

In order to contrast the difference of the resonant radiation force under local and nonlocal response,we also plot the resonant radiation force spectra for local and nonlocal cases in p-polarization in Fig.3.From Fig.3,we can find that the nonlocality of optical response has an important influence on the resonant radiation force spectra.Obviously,the resonance peak of Fxand Fzhas an evident blue-shift under nonlocal response,compared with those under local response with same conditions for p-polarized state.Furthermore,the amplitudes of Fxand Fzunder nonlocal response are larger than those under local response,respectively.In addition,for s-polarized state,both Fxand Fzare equal to zero under local response due to the y component of polarization PPP is equal to zero in dipole approximation.However,they are not equal to zero under nonlocal response.The radiation shift of the resonant radiation force spectra due to the nonlocality of optical response is also demonstrated by Eq.(19).From Eq.(19)we can easily see that the resonance structures of the optical force spectra are determined by the roots of detAccording to the expressions of the diagonal matrix elements Dxx,Dyy,and Dzz,it is obvious that the resonance peak does not occur at¯hω=ε21,but has a shift relative to the level interval ε21,which is attributed to the contributions from the real part of the terms hMxx,hMyy,tMzz,respectively.

Fig.3.Under local(solid lines)and nonlocal(dashed lines)response,the resonant radiation force spectra(Fxand Fz)in p-polarization for the well width:LR=LL=7 nm.The mid-barrier width LB=1 nm,and the barrier heightV1=V2=2.0 meV.¯hΓ0=0.47 meV.

To see how the well-width ratio and the polarized state influence the resonant radiation force spectra,we plot the maximum radiation force(Fxand Fz)at resonance in Fig.4 and the position of the resonance peak(¯hω/ε21)in Fig.5 versus the well-width ratio LR/LLin the two cases of p-and s-polarizations,respectively.The black solid,red dashed,and blue dotted lines correspond to the barrier height ratios V1/V2=0.4,0.7,and 1.0,respectively,with LL=4 nm and V2=2.0 meV.In Figs.4 and 5,it is evident that both the maximum radiation force and the position of the resonance peak are closely relevant to the structure parameters of the CQWN,and the changing trend of Fxand Fzversus the well width ratio LR/LLis consistent essentially for p-polarization and spolarization.From Fig.4,we can see that with the increase of the well width ratio LR/LL,the maximum resonant radiation force decreases at first and then rises;when LR/LL=1,that is,when the CQWN becomes symmetric,it attains a peak value.The CQWN degenerates to a single quantum well when LR/LL=0,and the resonant radiation force is maximal at this point.When LR/LL＞3.0,the resonant radiation force does not increase with further increasing the CQWN width.When the well width ratio value LR/LLis in the approximate range from 1.5 to 1.8,a relative minimal resonant radiation force can be obtained.Furthermore,for a fixed CQWN width ratio,the resonant radiation force becomes smaller and smaller with the increase of the mid-barrier height V1,when the width ratio LR/LLis in the range from 0.5 to 2.0.All the properties manifest that the resonant radiation force can be modulated by designing the structure parameters of CQWN.

Fig.4.The maximum resonant radiation force(Fxand Fz)versus the well-width ratio LR/LLin the two cases of p-and s-polarizations for V1/V2=0.4(black solid line),0.7(red dashed line),1.0(blue dotted line)respectively,with the left well width LL=4 nm,and the outer barrier heightV2=2.0 meV,¯hΓ0=4.7 meV.

Fig.5.The resonant peak position of optical force spectra,normalized by energy-level interval ε21,versus the well width ratio LR/LLwith the V1/V2=0.4(black solid lines),0.7(red dash lines),1.0(blue dot lines)in the two cases of p-polarization and s-polarization,respectively,with the left well width LL=4 nm,and the outer barrier heightV2=2.0 meV,¯hΓ0=4.7 meV.

The well width ratio LR/LLis an important factor in infl uencing the position of resonance peak of the optical force spectra,as shown in Fig.5.It is worth noting that the position of resonance peak would deviate from the energy interval ε21due to the nonlocal interaction between electrons and laser fields.As the well width ratio LR/LLincreases,the deviation of the resonance peak position is more and more evident; when LR/LL=1,the deviation attains to apeak value,and then it decreases gradually.In other words,the radiation shift of optical force at resonance in symmetric CQWN is larger than that in asymmetric CQWN generally.The reason is that,compared with asymmetric CQWN,the wave functions of symmetric CQWN would be broadened more due to stronger coupling effects between two wells of symmetric CQWN,which leads the characteristic response scale of electrons to increase.In addition,the barrier height also has influence on the radiation shift of the position of resonance peak of the optical force spectra in the two cases of p-polarization and s-polarization.It increases with the increase of mid-barrier height V1,and is larger in the p-polarized state.

The change of maximum resonant radiation force(Fxand Fz)with the barrier height ratio V1/V2is shown in Fig.6 for three different well width ratios:LR/LL=2.5/5(black solid line),LR/LL=5/5(red dash line),LR/LL=7.5/5(blue dotted line)in the two cases of p-polarization[(a)and(b)]and spolarization[(c)and(d)].We can see clearly in Fig.6 that the maximum resonant radiation forces(Fxand Fz)decrease gradually with the barrier height ratioV1/V2increasing at first,and then tending to remain stable.It is because that the coupling effect would be weaken with the mid-barrier height increasing.In addition,for a fixed barrier height ratio V1/V2,the change of maximum resonant radiation force(Fxand Fz)with the well width ratio LR/LLis also in agreement with those shown in Fig.3.

Fig.6.The change of maximum resonant radiation force(Fxand Fz)versus the barrier height ratio V1/V2for three different well width ratios:LR/LL=2.5/5,5/5,7.5/5 in the two cases of p-polarization[(a)and(b)]and s-polarization[(c)and(d)],respectively,with the left well width LL=5 nm,and the outer barrier heightV2=2.0 meV,¯hΓ0=4.7 meV.

In Fig.7,we show the maximum resonant force(Fxand Fz)versus the incident angle θ in the two cases of ppolarization[(a)and(b)],and s-polarization[(c)and(d)]for three different well-width ratios,respectively.We note that the maximum resonant radiation forces for the p-polarized state are much larger than those for the s-polarized state,except the case of θ=0.This is because there is a quantum-size effect for the p-polarized state,while it hardly works for the s-polarized state.Furthermore,we can see clearly that the incident angle has an evident influence on Fxand Fz.For ppolarized state,as the incident angle θ increases,it is obvious that both Fxand Fzincrease in Figs.7(a)and 7(b).This is because with θ increasing the z component of the incident field increases,causing an increase of the z component of the polarization PPeP(z,ω)in the CQWN,and the quantum-size effect plays an important role in the z direction.When θ =0°,which means that the incident light is perpendicularly incident on the CQWN,and the electronic polarization parallels to the x direction,as a result that Fzat resonance is very small because the quantum-size effect have not any influence in this direction.When θ =90°,that is,the incident light is horizontally incident on the CQWN,the electronic polarization direction is completely parallel to the z direction,which leads to Fxand Fzat resonance to be maximum on account of the quantum-size effects.For the s-polarized state,we can see that Fzdecreases and Fxincreases with the incident angle θ increasing in Figs.7(c)and 7(d).The reason for this is that the z component of wave vector will decrease and the x component will increase with the increase of incident angle,respectively.These properties make the CQWN a good candidate for optical manipulation of nano-objects using laser-induced radiation force.

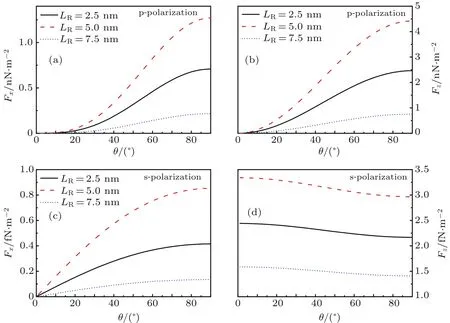
Fig.7.Maximum resonant radiation force(Fxand Fz)versus the incident angle θ in the two cases of p-polarization[(a)and(b)],and s-polarization[(c)and(d)]for three different well-width ratios,respectively,with the left well width LL=5 nm,and the barrier height V1=V2=2.0 meV,¯hΓ0=4.7 meV.

4.Conclusion

In this paper,we have theoretically investigated the nonlocal effects on optical force exerted on the AlGaAs/GaAs CQWN from the resonant intersubband transitions for two kinds of polarized states.We have shown that there exists a blue-shift of radiation force spectra at resonance caused by the spatial nonlocality of optical response,and with well width increasing,the radiation shift increases for symmetric CQWN,while it is more evident and larger than those for asymmetric CQWN.Moreover,it is also demonstrated that the resonant radiation force is controlled by the CQWN width ratio,the barrier height ratio,the polarized and incident directions of incident light.The designable CQWN provides a more advantageous way to obtain the suitable optical resonant radiation force.These properties have potential applications in detecting internal quantum properties inside nanostructures,and can open novel and exalting possibilities for the characterization,assembly and optical control of nano-objects.