粮食种植面积的影响因素分析*
2019-06-18马元魁张雪赟
马元魁,张雪赟,李 萍,刘 铎
(西安工业大学 理学院,西安 710021)
粮食的种植面积是决定粮食供给的关键因素,也是保障粮食安全的重要前提。比较政策实施前后粮食种植面积是否有显著性变化,可以用来衡量粮食最低收购价政策实施的效果。可能影响粮食种植面积的因素有很多,除了粮食最低收购价政策外,还可能有其他很多的影响因素,如农业劳动力人口、粮食进出口贸易、农民受教育程度、城乡收入差距、家庭负担等。
不少学者以不同方式研究构建粮食种植面积影响因素体系。在研究方法方面,主要有因子分析建模[1]、Person 相关系数分析[2]、多元线性回归模型[3]、主成份分析法[4]等。得到的影响因素主要有人力、物力投入以及粮食平均价格[1],有效耕地面积、受灾面积以及粮食最低收购价格[2,5],进出口差额和复种指数[3],粮食产量、城乡收入差距[4,6],农资费用以及化肥施用量等[7]。学者们得出了保证粮食种植面积,实行粮食价格补贴和最低收购价政策的重要性。
为了确定影响粮食种植面积的因素,本文拟从不同粮食品种的角度出发,找出可能的影响因素,对其进行相关性分析,筛选出显著相关的指标,使用SPSS进行多元线性回归分析,并从模型的整体显著性、拟合优度以及误差分析方面进行模型可靠性检验。
1 各评价指标对全国小麦种植面积的影响
影响小麦种植面积的相关评价指标有很多,本文选取了其中一些评价指标,主要有小麦的最低收购价、小麦的产量、小麦的产值、小麦的生产成本、净利润、城乡收入差距以及上一年种植面积等。选取2004-2013年10年间7个评价指标的相关数据,数据来源于《全国统计年鉴》和全国统计公报以及国家发改委等部门的小麦和稻谷的最低收购价格执行预案[8-10]。
1.1 小麦种植面积及其部分评价指标进行相关性分析
比较各个评价指标与当年全国小麦种植面积之间是否具有相关性,若相关性显著,则说明此评价指标是一个很重要的影响因素;若相关性不显著,则说明此评价指标对种植面积影响不大,可将此评价指标剔除。
用SPSS统计软件对当年小麦种植面积与评价指标的相关性进行分析,结果见表1。
从表1可以看出,小麦产量、产值、小麦的生产成本、城乡收入差距及上一年的种植面积的显著性小于0.05,即与当年小麦种植面积相关性显著,小麦的最低收购价和小麦的净利润的显著性大于0.05,即与当年小麦种植面积相关性不显著,故此评价指标可以剔除。

表1 小麦种植面积与评价指标的相关性
1.2 模型建立
建立如下线性回归模型:
y=β0+β1x1+β2x2+β3x3+β4x4+β5x5+ε
其中:x1为小麦的产量;x2为小麦的产值;x3为小麦的生产成本;x4为城乡收入差距;x5为上一年小麦的种植面积。
使用SPSS统计软件对小麦种植面积与各指标体系进行参数估计,结果见表2。表2中的回归系数给出了模型中的估计值,得到回归方程为:
y=22 919.402-1.045x1-7.694x2-
15.277x3+1.207x4+0.032x5
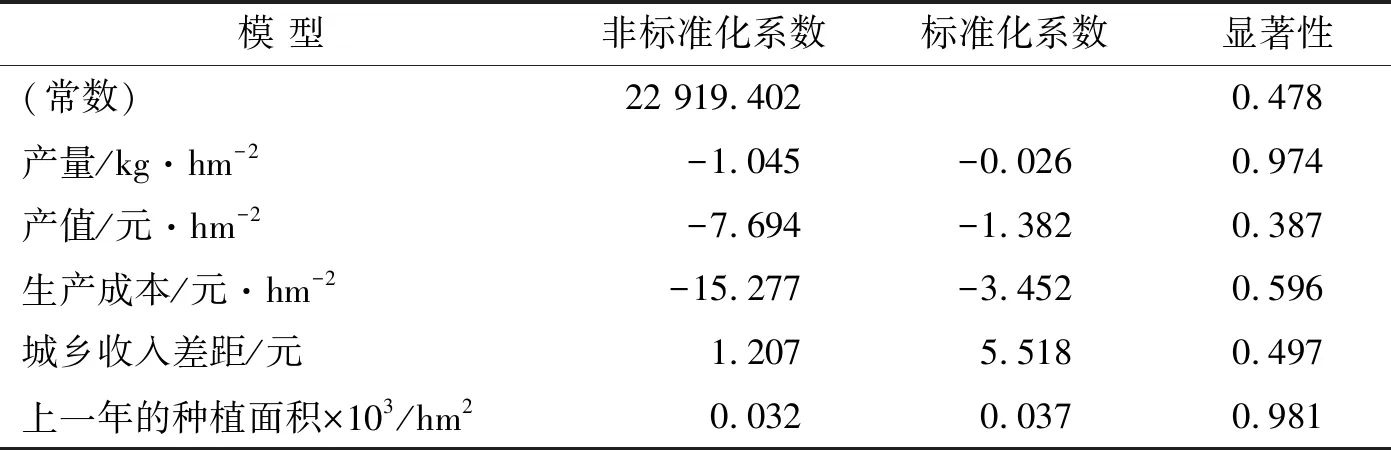
表2 参数估计结果
1.3 可靠性分析
模型预测的小麦的种植面积与当年小麦真实种植面积的误差分析结果见表3。结果表明整个模型拟合的相对误差较小,拟合精度较高。

表3 误差分析结果
2 各评价指标对全国稻谷种植面积的影响
影响稻谷种植面积的相关评价指标有很多,本文同样选取了稻谷的最低收购价、稻谷的产量、稻谷的产值、稻谷的生产成本、净利润、城乡收入差距及上一年的种植面积等。选取2004-2013年 10年间这7个评价指标的相关数据,数据来源于《全国统计年鉴》和全国统计公报以及国家发改委等部门的小麦和稻谷的最低收购价格执行预案[8-10]。
2.1 稻谷种植面积及其评价指标相关性分析
稻谷种植面积与评价指标的相关性见表4。从表4中可以看出,稻谷的最低收购价、产量、产值、生产成本、城乡收入差距及上一年的种植面积的显著性小于0.05,即与当年稻谷种植面积相关性显著;净利润的显著性大于0.05,即与当年稻谷种植面积相关性不显著,故此评价指标可以剔除。
2.2 模型建立
建立如下线性回归模型:

其中:x1为最低收购价;x2为稻谷的产量;x3为稻谷的产值;x4为稻谷的生产成本;x5为城乡收入差距;x6为上一年稻谷的种植面积。用SPSS统计软件对稻谷种植面积与各指标体系进行参数估计,结果见表5,表5中的回归系数给出了模型中参数的估计值,因此回归方程为
y=23 385.364+826.083x1-4.192x2+0.731x3-
3.036x4+0.165x5+0.205x6
2.3 可靠性分析
使用SPSS软件对该回归模型的整体效果进行评估得到的结果见表6、表7。其中对应的模型F值为32.706,远远超过F检验的临界值2.98,P值为0.008,小于0.05 ,表明模型是显著的,具有一定的可信度及稳定性。对于整个模型的拟合情况,其中调整后复判定系数R2的值达到了0.955,表明整个模型的拟合精度高。
模型预测的稻谷的种植面积与当年稻谷真实种植面积的误差分析结果见表8,结果表明整个模型拟合的相对误差很小,拟合精度较高。

表4 稻谷种植面积与评价指标的相关性

表5 参数估计结果

表6 双参数分析结果

表7 模型拟合优度检验
表8误差分析结果
Tab.8 The results of error analysis

年 份真实值预测值绝对误差相对误差/%200428 379.0028 387.568.560.030 0200528 847.4028 771.8075.600.262 1200628 937.9028 949.1411.240.039 0200728 918.8029 086.84168.040.581 0200829 241.0029 117.58123.420.422 1200929 626.9229 540.5686.360.291 5201029 873.4029 822.4051.000.170 7201130 057.0430 050.506.540.021 7201230 137.1130 164.9427.830.092 0201330 312.0030 308.763.240.010 7
3 结 论
本文对实行粮食最低收购价的小麦和稻谷分别进行研究,使用SPSS统计软件,对影响种植面积的各评价指标进行相关性分析,筛选出显著相关的指标,建立回归模型;并从模型的整体显著性、拟合优度以及误差分析方面进行模型可靠性检验,结果显示模型可靠性高。
影响小麦种植面积的因素为小麦的产量,小麦的产值,小麦的生产成本,城乡收入差距,上一年小麦的种植面积。影响稻谷种植面积的因素为最低收购价,稻谷的产量,稻谷的产值,稻谷的生产成本,城乡收入差距,上一年稻谷的种植面积。影响小麦和稻谷种植面积的因素不同,因此影响粮食种植面积的因素会因为粮食品种的不同也有所差异。
