履腿复合式移动机器人的轨迹跟踪控制与实现

李艳杰，何乃峰，范晓亮

(1.沈阳理工大学 机械工程学院,沈阳 110159；2.泰州市翔达消防器材有限公司，江苏 泰州 225300；3.中国科学院沈阳自动化研究所 机器人学国家重点实验室,沈阳 110016)

自主导航和运动控制是移动机器人自主性的关键指标和核心技术，具有自主导航与运动能力的移动机器人在国防、救援、科考、服务、工业等几乎所有移动应用领域都存在着广泛的需求，应用前景极其广阔。伤员救援、关键设施巡检是移动机器人的典型应用，在这些应用场景中，为了确保伤员人身安全和关键设施设备安全，往往要求机器人精确沿规划路径和轨迹运动。轨迹跟踪是指移动机器人跟踪期望轨迹时的位置、速度、加速度的时间历程[1]。

履腿复合式移动机器人在伤员救援、关键设施巡检领域具有很高的实用性。本文利用Backstepping控制算法实现了具有差动转向特征的履腿复合式移动机器人的轨迹跟踪控制，并进行了实验验证。

1 轨迹跟踪技术的研究现状与进展

近几十年来，针对机器人轨迹跟踪控制问题，国内外相关学者和研究团队在方法的理论研究和实验验证方面已开展了大量工作，针对具体应用，这些方法各有千秋。

基于PID的轨迹跟踪算法是研究得较早且较多的一种轨迹跟踪控制方法。PID控制方法不需要精确的控制模型，方法简单易实现，但当PID参数设置不当时，可能导致跟踪的误差变大、电机工作不平稳。文献[2-3]利用PID控制方法，实现了对轨迹的跟踪控制。文献[4]提出了一种新的滑膜控制方法，利用李雅普诺夫定理证明了该滑膜控制系统渐进稳定，在考虑移动机器人系统受外界环境干扰的情况下，此方法具有较高的轨迹跟踪精度，并且有效的抑制了移动机器人抖震问题。但是存在人为的主观因素，并且在控制过程中不能及时地对参数进行修正，会严重的影响实验结果。文献[5]基于迭代学习控制方法研究了农业车辆轨迹跟踪控制问题，该方法根据过去运行的次数信息，修正当前的控制输入信号，来实现高精度的轨迹跟踪控制。该算法的特点是结构简单、计算量小、易于实际系统的实现。文献[6]研究了一种新型的基于模糊控制的轨迹跟踪方法，首先使用模糊建模方法，将具有参数变化的原始非线性轨迹跟踪系统构造成具有T-S模糊模型加性范数有界不确定性，然后在Lyapunov框架下提出了一种基于模糊观测器的车辆动态输入反馈控制方法。文献[7]针对具有非完整约束的双差速驱动移动机器人的轨迹跟踪问题，提出了先建立速度协同条件的非线性运动学模型并通过在线整定参数，再提出一种融合偏差能转化为评价函数法和指数法稳定控制的混合控制律。该混合控制律可平滑转化偏差状态、同步消除位姿偏差，使得移动机器人更加精确、稳定地跟踪期望轨迹。文献[8]中基于在线强化学习轨迹跟踪控制，采用模型预测控制算法与在线强化学习对移动机器人进行轨迹跟踪控制，通过计算输入序列，使轨迹跟踪误差最小化。文献[9]中提出了一种基于反步动力学控制和自适应神经网络调节滑膜增益的PI型滑模动态控制的混合算法。该算法是利用径向基神经网络来调整滑膜控制增益，消除滑膜控制输入抖动和优化系统性能。

在以上几种轨迹跟踪的方法中，大多数方式都是在局部环境中性能稳定，无法实现全局调节或者跟踪，达不到期望的系统所需要的轨迹跟踪控制性能。基于此，本文使用Backstepping方法，该方法适用于可以控制相对阶为n的非线性系统，消除了经典无源性设计中相对阶为1的限制[10]。

本文利用Backstepping控制算法，实现履腿复合式移动机器人的轨迹跟踪控制。在建立移动机器人运动学模型的基础上，利用Backstepping控制律实现该移动机器人的轨迹跟踪控制，并将该算法与PID算法进行实验对比。

2 履腿复合式移动机器人的轨迹跟踪控制与实现

2.1 移动机器人介绍

图1为中科院沈阳自动化研究所研制的履腿复合式移动机器人。

该移动机器人重量仅仅只有25kg，最大的载重为15kg，在野外最大速度可达1m/s。机器人可搭载多种传感器或者机械臂用于不同目标的实验与研究。该移动机器人共有4个自由度，可以在水平面内移动和转动。该移动机器人还有两个小摆臂。移动机器人的两条主履带分别由两个直流有刷电机驱动，通过等速控制移动机器人在水平面内进行前进或者后退，通过差动控制移动机器人实现任意半径内的转弯。通过对小摆臂电机的正反转控制可以实现移动机器人质心位置的变化，使得移动机器人在复杂的地面环境下保持稳定，可以实现跨越0.2m障碍物的功能。

图1 履腿复合式移动机器人

2.2 基于Backstepping轨迹跟踪控制方案

针对履腿复合式移动机器人运动机构特点，提出基于Backstepping方法的轨迹跟踪总体控制方案，如图2所示。

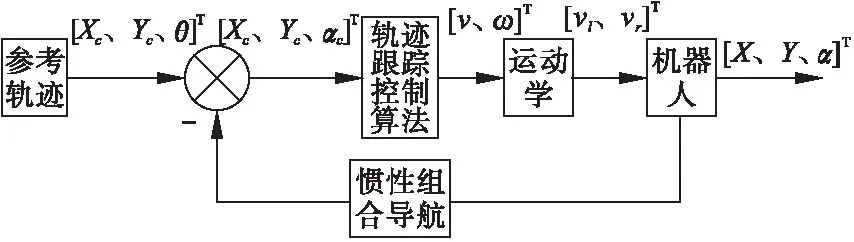
图2 移动机器人轨迹跟踪控制原理图

2.3 问题描述与坐标系定义

为了方便描述移动机器人的运动，定义了两个平面直角坐标系，如图3所示。

图3 移动机器人位姿误差示意图

图3中，是基于当前环境下的全局坐标系XOY以及是基于移动机器人本身的局部坐标系xoy。全局坐标系定义了移动机器人在实际工作情况下的坐标原点、X轴的方向与Y轴的方向，坐标原点为地球上的任意一点的经纬度，X轴正半轴代表着正北方向，Y轴正半轴代表着正西方向，并且每个点的全局坐标系都是固定的，是不可移动的。在局部坐标系中，局部坐标系的坐标原点与移动机器人的质心A相重合，车头前进的方向是y轴，x轴代表着移动机器人的横向，但是局部坐标系的x轴与y轴的方向是随着车体前进的方向变化而变化的。

2.4 位姿误差

在全局坐标系中，移动机器人的当前位姿矢量PA表示为[XA,YA,α]T，其中XA、YA系原点在全局坐标系下的坐标，α为移动机器人坐标系y轴与全局坐标系Y轴的夹角。移动机器人下一个目标位姿PC表示为[XC,YC,β]T。θ为移动机器人目标位姿与实时位姿之间的夹角。

在全局坐标系坐标系XOY中，当前位姿PA点到目标点PC的位姿误差表示为

(1)

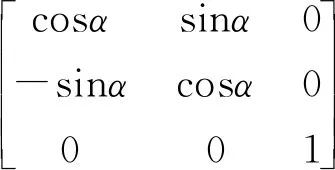
2.5 自适应跟踪控制律的设计

Backstepping设计方法是针对不确定性系统的一种系统化控制器综合方法，是将Lyapunov函数的选取与控制器的设计相结合的一种回归设计方法。该设计方法之所以受到国内外学者的极大关注，主要原因是该方法消除了系统不确定性，将复杂的非线性系统分解为了不超过系统阶数的子系统，从而解决了相对复杂的非线性系统的控制问题。针对履带与地面摩擦的滑移非线性特点，采用Backstepping算法实现履腿复合式移动机器人轨迹跟踪控制律。

根据Backstepping建模方法，容易得到履腿复合式移动机器人跟踪控制律[11-12]为

(2)

式中：υc、ωc分别为移动机器人当前位置的速度与角速度，Xe、Ye、αe分别为移动机器人的X轴方向的误差、Y轴方向的误差、方位角的误差。k1、k2、k3均为大于零的常数。

2.6 移动机器人运动学模型

履腿复合式移动机器人轨迹跟踪最终通过双侧履带电机控制实现，因此，需要确定移动机器人线速度与角速度控制量(v,ω)T到左右两侧主履带驱动电机的速控制量vl与vr。基于差速运动原理，(v,ω)T与(vl,vr)之间的数学转换模型如下。

(3)

式中：B为车体的宽度；b为履带的宽度；i为减速比。

3 实验

利用Backstepping的轨迹跟踪控制算法实现了履腿复合式移动机器人的直线与圆两种典型轨迹跟踪实验，并与基于PID的轨迹跟踪控制算法进行了实验对比。

3.1 直线轨迹跟踪试验

在直线轨迹跟踪实验中，直线轨迹由起点和终点确定，起点GPS坐标为经度：123.44085241，纬度：41.76119061，终点GPS坐标是经度：123.44081983，纬度：41.76132336。设轨迹跟踪目标速度为vc=0.6m/s,期望角速度为ωc=0rad/s。

选取Backstepping轨迹跟踪控制律参数为k1=5.2、k2=25、k3=5.2。

PID轨迹跟踪控制算法的参数选为P=2、I=1、D=4。

移动机器人起始点的GPS坐标为经度123.44085241，纬度41.76119061，航向角60°。

基于Backstepping的轨迹跟踪控制算法的实际跟踪轨迹如图4所示，PID的轨迹跟踪控制算法的实际跟踪轨迹如图5所示。两种算法轨迹跟踪误差如图6所示。

图4 基于 Backstepping方法的直线轨迹跟踪曲线

由图6可看出，基于Backstepping的轨迹跟踪误差最大值为0.5m，基于PID的轨迹跟踪误差为1m，对比实验结果表明，基于Backstepping的轨迹跟踪方法较基于PID的轨迹跟踪算法，具有更高的直线轨迹跟踪精度。

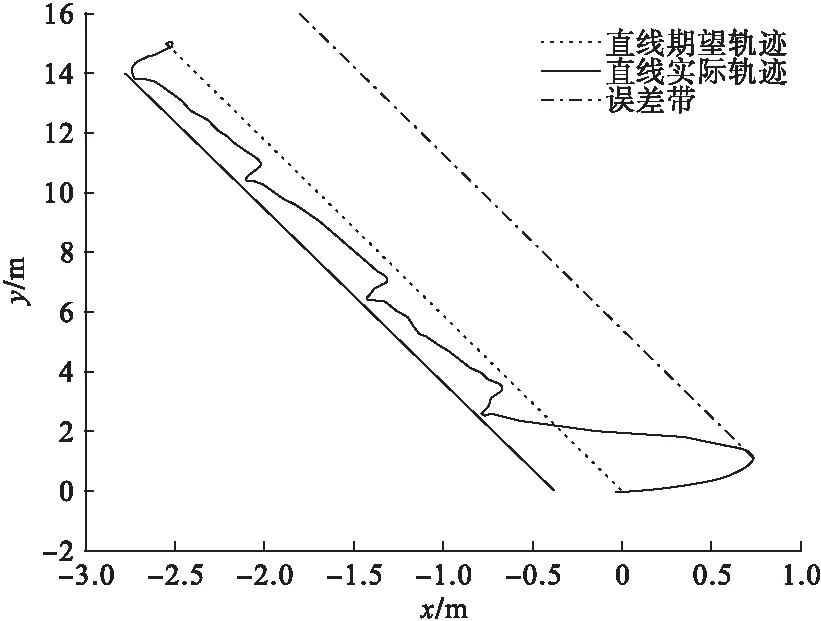
图5 基于PID方法的直线轨迹跟踪曲线

图6 两种方法直线轨迹跟踪误差对比图

3.2 圆形轨迹跟踪试验

在圆形轨迹跟踪实验中，设圆形轨迹圆心点的GPS坐标是经度123.44072956，纬度41.76103523，半径为9.7m。轨迹跟踪目标速度为vc=0.6m/s、期望角速度ωc=0.2rad/s。

Backstepping的轨迹跟踪控制律参数为k1=3、k2=8、k3=3。

PID轨迹跟踪控制算法的参数选为P=3、I=1.5、D=2。

基于Backstepping的轨迹跟踪控制算法的实际跟踪轨迹如图7所示，基于PID的轨迹跟踪控制算法的实际跟踪轨迹如图8所示。两种算法轨迹跟踪误差如图9所示。

由图7、图8、图9可看出，使用Backstepping方法得到的轨迹跟踪，误差带为0.8m。使用PID方法得到的轨迹跟踪，误差带为1.5m。可见在圆形轨迹跟踪中，Backstepping控制算法同样条件下比PID控制算法的轨迹跟踪误差更小。

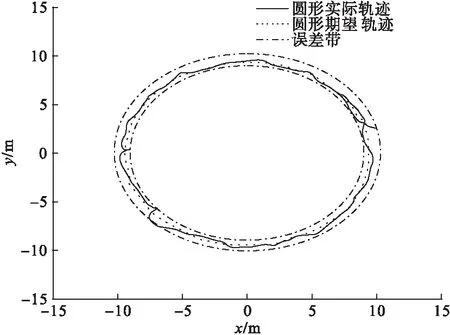
图7 基于Backstepping方法的圆轨迹跟踪曲线

图8 PID方法的圆轨迹跟踪曲线

图9 两种方法圆形轨迹跟踪误差对比图

4 结论

建立履腿复合式移动机器人运动学模型，设计基于Backstepping算法的轨迹跟踪控制律；利用控制律，针对实际常用的直线和圆两种轨迹，完成履腿复合式移动机器人的轨迹跟踪控制实验，并与PID轨迹跟踪控制算法进行对比实验。实验结果表明基于Backstepping的轨迹跟踪控制算法具有较高的轨迹跟踪精度，初步测试验证了基于Backstepping方法的轨迹跟踪算法在差速转向的履腿复合式移动机器人自主运动控制中的可行性。