如何找到思维的开窍点

陕西省咸阳师范学院基础教育课程研究中心 安振平

1．问题呈现

笔者看到，唐秀颖先生主编的《数学题解辞典（平面解析几何）》（上海辞书出版社，1983，06）一书的第38题为：

问题1-1：已知三平行线l1，l2，l3．l1与l2之间，l2与l3之间的距离分别为a，b．正△ABC的三顶点分别在l1，l2，l3上．求此正三角形的边长．

这道经典的题目，通过加工，竟然出现在2007年四川高考理科卷上．

问题1-2：如图1，l1，l2，l3是同一平面内的三条平行直线，l1与l2间的距离是1，l2与l3间的距离是2，正△ABC的三顶点分别在l1，l2，l3上，则△ABC的边长是（ ）

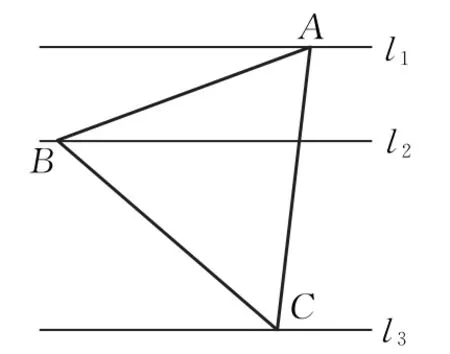
图1

2．解题分析

本考题条件简明，情境设置独特，不少考生望而生畏，不知如何求解．

解题思维的起点，来自于深度的理解题意，翻译题意，实施文字语言、图形语言和符号语言的转化．把平行直线“l1与l2间的距离是1，l2与l3间的距离是2”显示为图形语言，就需要作出题目中平行线的垂线段，垂线段作在哪里呢？

分析1 设出正三角形的边长，通过勾股定理，建立方程．

解法1 如图2，过点A作AF⊥l3交l2于点E，交l3于点F，过点B作BD⊥l3交l3于点D．则AE=1，BD=EF=2．

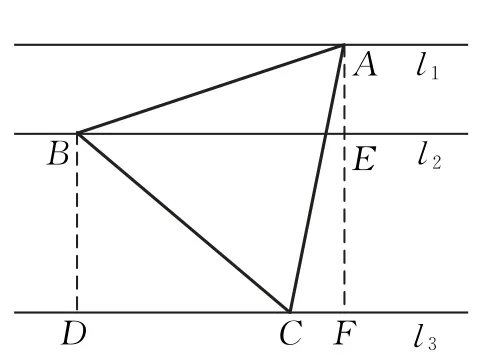
图2

设正△ABC的边长为x．

对Rt△BCD，Rt△ACF和Rt△ABE，应用勾股定理，得

注意到DC+CF=DF=BE，

这是一个无理方程，如何求解呢？化无理为有理，平方技巧啊！

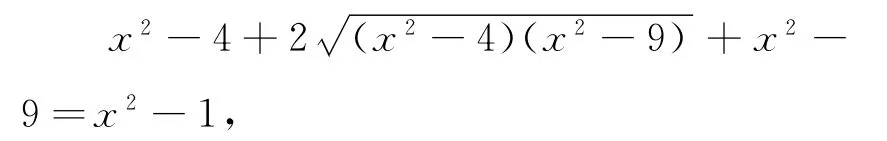
整理得

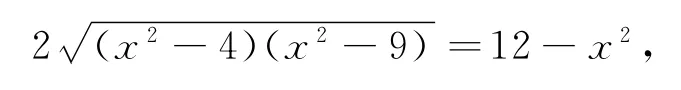
对上述方程两边平方，得

4（x2-4）（x2-9）=（12-x2）2，

整理为标准的一元二次方程，有

3x4-28x2=0．

说明 本解法用到的知识仅局限于初中范围，设元，构造方程，把无理方程转化为有理方程，检测了考生的基本运算能力．当中的“平方两次”的技巧，这是高中教材“椭圆标准方程”的推导过程中用过的方法．当然，本方程也可以探究其他的技巧解答方法，留给读者去完成．

解题思维的要害、开窍点在哪里呢？同一条线段DF的长度“算两次”．对三个直角三角形，应用了三次“勾股定理”．

分析2 设出正三角形的边长和图2中Rt△ABE的一个内角，通过锐角三角函数的定义，建立方程组．

解法2 如图2，设正△ABC的边长为x，∠ABE=θ，则∠EBC=60°-θ=∠BCD．

对Rt△ABE，Rt△BCD，应用锐角三角函数的定义，有

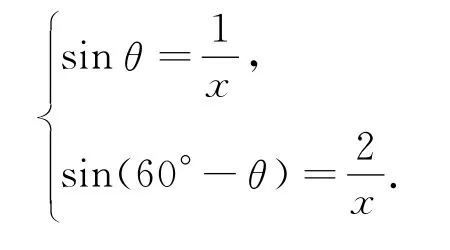
对这个方程组，为求边长x，可以先求sinθ的值，为此，先消去x，得

sin（60°-θ）=2sinθ，

3（1-sin2θ）=25sin2θ，

说明 本解法在列方程组时，仅用到初中范围的知识，但解答需要用到高中的三角公式．巧妙设出角度，应用方程组的观点，借助三角恒等变形，代数运算量要简单一些．

解题思维的要害、开窍点在哪里呢？在于巧设角度和边长两个变量！对两个直角三角形，两次应用了“正弦的定义”．

分析3 从图3中两个直角三角形的相似，设出正三角形的边长，而后应用余弦定理、三角形面积公式构造方程，通过方程方法求解之．

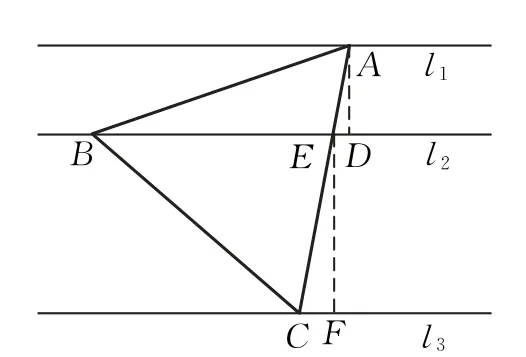
图3

解法3 如图3，过点A作AD⊥l2于点D，过点E作EF⊥l3于点F．则AD=1，EF=2．

显然Rt△ADE∽Rt△EFC，则有

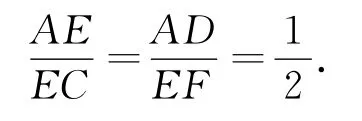
设AE=x，则EC=2x，正△ABC的边长为3x．

对△ABE，应用余弦定理，有

BE2=AB2+AE2-2AB·AE cos 60°，

下面研究△ABC的面积：

一方面，

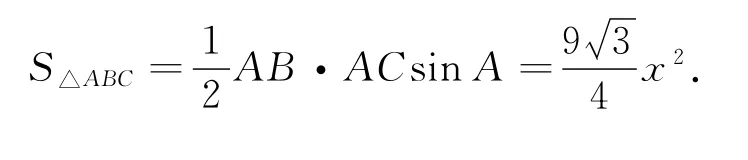
另一方面，

说明 本解法在计算三角形面积时，既用到小学教材里的三角形面积公式，又用到了高中教材里的三角形面积公式，这是最为核心的基础知识．

解题思维的要害、开窍点在哪里呢？同一个三角形的面积，从不同角度“算两次”，就自然获得了需要的方程．

看来，在用条件的过程里巧设、妙列，才可能简单求解．当中，“设、列、解”，值得玩味！

3．变式思考

思考1 对上述解法1里获得的方程，给出类似的问题，就有：

问题2-1：解方程

思考2 把问题2-1里的“根号”改为“绝对值号”，并将“等号”改为“不等号”，就有：

问题2-2：解不等式|x-3|+|x-2|≤|x-1|．

思考3 如果把问题2-1左面的“根号”改为“绝对值号”，就有：

问题2-3：解方程|x-3|+|x-2|=

对于问题2-3，也许你会立即“观察”出它有一个根2！大胆猜想之后，还需要小心求证．还有其他根吗？且行且思．

思考4 更进一步，通过变式探究，还可以获得：

问题2-4：求方程|x-2|+|x-1|+|y|=3表示的曲线所围区域面积．

图4

解 由|x-2|+|x-1|+|y|=3和0≤|y|，得|x-2|+|x-1|≤3，解得0≤x≤3．

当y≥0时，方程|x-2|+|x-1|+|y|=3转化为函数

显然，方程|x-2|+|x-1|+|y|=3表示的曲线关于x轴对称．于是，可以画出该方程表示的整个曲线，其所围区域的面积

说明 发现了方程表示曲线的对称性，从“方程”变更为“函数”就显得那么自然，区域的“直观”呈现就水到渠成．

数学解题，需要逻辑推理，需要数学抽象，需要构造模型，更需要代数变形和几何直观．转化的功力是解题能力的具体呈现，把陌生问题熟悉化，复杂问题简单化，未知问题已知化．正如上文中的“无理化有理”“几何化三角”“绝对值化分段”等等．

我们可以从这样的分析问题、发现问题、提出问题和解决问题的“修炼”过程中，体验数学学习的奇妙，感悟数学思维的味道．