空间角度复合应变估计中的运动伪影产生因素研究

2019-06-17潘宗辉刘志李富峰何琼

中国医疗设备 2019年5期

潘宗辉，刘志，李富峰，何琼

清华大学医学院生物医学工程系，北京 100084

引言

中风是全世界死亡率第二的疾病，而在中国则是头号杀手[1]。其中，颈动脉粥样硬化斑块的破裂是导致缺血性中风发生的主要原因之一[2]，因此，对斑块的易损性进行早期评估有助于预防缺血事件的发生。在组织学上，易损斑块通常具有大的脂质核、薄的纤维帽、斑块内出血、炎症以及新生血管等特征，而稳定斑块则通常有钙化、厚的纤维帽以及没有脂质核[3]。因此，根据斑块的不同成分特征，我们可以对斑块的易损性进行有效评估[4]。

目前已经有多种影像技术可以用于颈动脉斑块易损性的评估，如X射线电子计算机断层扫描（Computed Tomography，CT）、磁共振成像（Magnetic Resonance Imaging，MRI）和超声成像（Ultrasound Imaging）等[5]。CT会对人体产生电离辐射危害，MRI扫描价格较为昂贵且耗时长[6-8]，超声成像具有扫描价格相对便宜、实时成像、无电离辐射危害等优势，近年来，超声弹性成像技术被提出用来识别易损斑块[9]。弹性成像方法首先被应用于血管内超声（Intravascular Ultrasound，IVUS）来区分稳定和易损的冠状动脉斑块[10-12]。虽然IVUS弹性成像具有较高的灵敏度和特异度，但是它具有侵入性且费用昂贵。鉴于IVUS的局限性，有研究者开始发展非侵入性血管弹性成像技术，例如颈动脉弹性成像[13-16]。颈动脉弹性成像通过运动估计方法算出斑块的位移和应变（率）分布[17-18]，然而低精度的侧向估计降低了短轴扫描下的成像性能。为了提高侧向估计的精度，近年来有研究者已经提出了侧向插值算法和在侧向点扩散函数上加振荡的方法[19-20]。

空间角度复合（Spatial Angular Compounding，SAC）成像是另一种提高侧向估计精度的方法[21-24]。在多角度平面波SAC中，轴向（竖直）位移和侧向（水平）位移都是通过多个角度的轴向位移复合得到的。如图1理想情况所示，我们分别在物体形变前和形变后采集多个角度的射频（Radiofrequency，RF）数据，并通过二维互相关算法分别得到沿各个角度方向的轴向位移。随后，最终的轴向位移uver和侧向位移uhor可以通过最小二乘法从这些轴向位移中重建得到，其具体公式如下：

其中AT是矩阵A的转置，θi（i=0,1，...，n）是转向角，n是NSA，uax，θi则代表沿偏转角θi的轴向位移。

上述情况考虑的是准静态弹性成像过程，即对物体施加一个静态压缩，分别在压缩前后对物体成像，进而得到位移估计。然而在实际情况中，物体在多角度发射过程中也有运动和形变，这可能会导致运动伪影的产生。图1分别展示了基于理想情况和实际情况下的SAC成像过程，我们设定空间复合的角度数量为3（即NSA=3），PRF保持不变，物体的高度为h。在理想情况下，我们在对物体施加2%的压缩前后各采3个角度的数据，获得各个角度下的位移估计，进而通过角度复合得到更准确的结果。在实际情况下，在多个角度发射过程中，应变率固定为σ的轴向应变被施加到物体上表面，用来模拟物体在SAC过程中的运动和形变。当σ较小或PRF足够高时，可以认为不同偏转角下的数据是同时获得的，因此相邻角度的发射过程之间没有运动伪影。然而在实际的颈动脉弹性成像中，当PRF不够高或NSA过多时，斑块的运动和形变将不能忽略，可能会产生运动伪影。

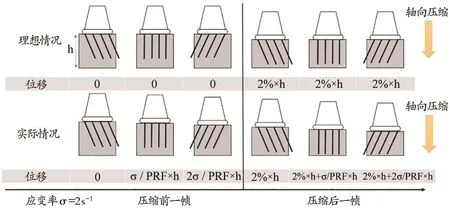
图1 基于理想情况和实际情况下的SAC成像

为了研究PRF和NSA这两个因素对SAC中运动伪影的影响，我们在仿真中分别模拟了理想情况和实际（有伪影）情况。如图1所示，在理想情况下，施加2%形变前，物体在三个角度的发射过程中位移始终为0，在施加2%形变后，物体的位移也保持不变（2%×h）。在实际情况下，施加2%形变前，物体在每两个相邻角度的发射之间发生了一段位移（σ/PRF×h），同理可知，施加2%形变后，物体在每两个相邻角度之间也会发生位移（σ/PRF×h），叠加2%的形变后就是物体形变后在每个角度下的位移值。

1 方法

1.1 仿真设置

在有限元分析软件FEMLAB 3.5a（Comsol Inc.,Burlington, MA, USA）中，我们构建了一个三维数值仿体。该仿体的尺寸为40 mm×40 mm×6 mm（深度×宽度×厚度），其中心嵌入一个直径为4.05 mm的圆柱形异物。圆柱形异物和周围背景的杨氏模量分别为80 kPa和25 kPa。

许多学者都采用该模型对应变成像的基本参数进行研究，这种结构简单的模型也比较适合对基本成像方法或参数进行早期研究[18]。为了模拟颈动脉弹性成像过程中斑块的运动和形变，我们对物体施加了一个轴向压缩。颈动脉斑块的轴向应变率一般不超过2 s-1，因此仿真中该轴向压缩的应变率设为 2 s-1[14]。

我们用Field II软件模拟了一个具有192阵元的线阵探头，其有效阵元数为128[25-26]，并将仿体放置在探头下方10 mm处进行成像。探头的阵元间距设为0.20 mm，中心频率设为6.25 MHz，采样率设为100 MHz。在控制探头发射过程中，我们设置了多组不同的PRF和NSA。PRF的变化范围是200 Hz～10 kHz，基本涵盖了超声机器常用的PRF范围，具体包括 200 Hz，500 Hz，800 Hz，1 kHz，1.5 kHz，2 kHz，3 kHz，4 kHz，5 kHz，6 kHz，8 kHz，10 kHz。我们在设置发射角度时都包含0°以提高轴向估计的精度，且正负角度对称，因此NSA都是奇数。常用的SAC角度有3和7，且PRF较低时设置9个或者更多的角度数量会带来更大的伪影问题。因此，NSA 取值为 1（0°），3（0°，±15°），5（0°，±7.5°，±15°）和 7（0°，±5°，±10°，±15°）。

1.2 超声仿真数据收集和处理

首先，我们以Field II软件对数值仿体进行仿真计算，获得仿体形变前的超声通道数据。接着，我们按照图1介绍的方法对仿体施加轴向压缩产生形变。仿体初始的散射子密度设为12.5个/mm3，其位置和幅度均为随机分布。形变后仿体中散射子的位置是通过FEMLAB仿真得到的理论位移加上形变前散射子的位置获得，而其幅度保持不变。然后，我们再次用Field II软件对形变后仿体进行仿真计算，获得相应的超声通道数据。最后，我们采用一个基于汉宁窗和f-number为1.5的延时叠加（Delay and Sum，DAS）算法分别对形变前后的超声通道数据进行波束合成计算，获得波束合成后的RF数据。

1.3 应变计算

我们利用基于光流法的SAC（窗长：2.0mm×2.0 mm）来分别对形变前后的RF数据进行处理，以得到轴向和侧向位移估计分布。随后，我们再用窗长为0.5 mm×0.5 mm的二维中值滤波器来去除位移场中的离群值。最后，我们用Savitzky-Golay（SG）差分器对滤波后的轴向和侧向位移进行差分，来得到相应的轴向和侧向应变图像[27]。这里，SG差分器在轴向和侧向的长度分别为1.0 mm和2.0 mm。

1.4 成像性能评估

我们用SNR和CNR作为应变估计结果的评估标准。这里，SNR的定义如下所示：

其中，es是感兴趣区域（Region of Interest，ROI）中轴向或侧向应变的平均值，而σs是应变估计的标准差(Standard Deviation，SD)。

CNR的定义为：

2 结果

数值仿体在2%压缩量的形变下，设定不同PRF和NSA所得到的轴向应变图像如图2所示，而侧向应变图像如图3所示。轴向应变方面，我们可观察到，没有使用SAC的轴向应变图像（图2b）的周围背景，不如在PRF=5 kHz和NSA = 3时使用SAC（图2c）得到的背景均匀。此外，同样是NSA=3的SAC，PRF=5 kHz时的轴向应变图像（图2c）背景，比PRF = 0.5 kHz时的（图2d）更接近理论结果（图2a）。当PRF=0.5 kHz时，与NSA=3的轴向应变图像（图2d）相比，NSA=7的图像（图2e）中心不再是圆形，且周围背景更不均匀。侧向应变方面，我们可观察到，没有使用SAC的侧向应变图像（图3b）的异物变小，不如在PRF=5 kHz和NSA=3时使用SAC得到的侧向应变图像（图3c）。图3c的结果更接近理论结果（图3a）。此外，同样是NSA=3的SAC，PRF=0.5 kHz的侧向应变图像（图3d）出现了多个低应变的蓝色区域，与理论结果（图3a）的差异较大，且周围背景不如PRF=5 kHz（图3c）时均匀。当PRF=0.5 kHz时，与NSA = 3的侧向应变图像（图3d）相比，NSA=7时图像（图3e）的低应变蓝色和高应变红色区域出现了更大程度的位置偏移。

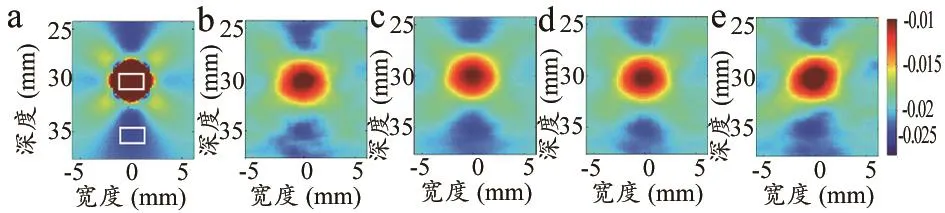
图2 数值仿体的轴向应变图像

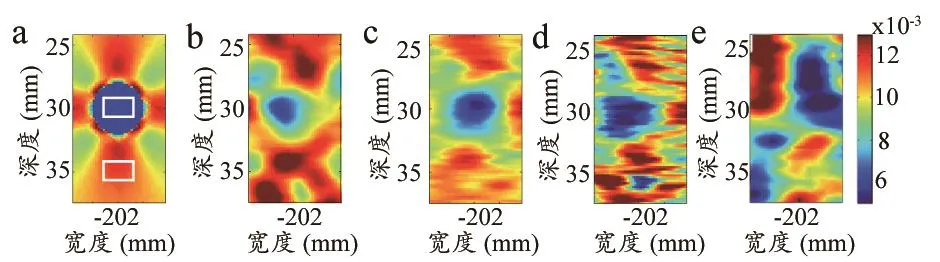
图3 数值仿体的侧向应变图像

不同PRF和NSA下轴向应变和侧向应变的SNR和CNR如图4所示。

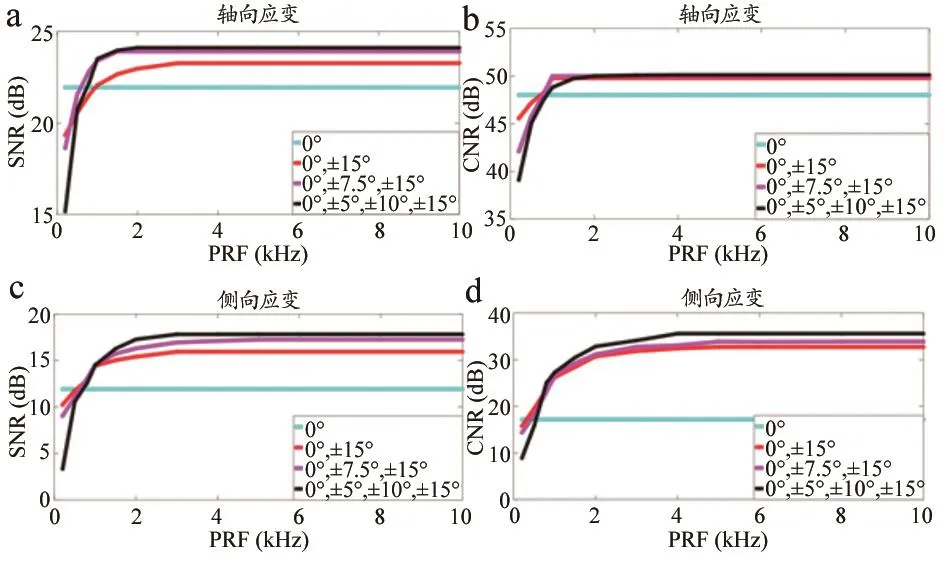
图4 不同PRF和NSA下轴向应变和侧向应变的SNR和CNR

其中，NSA=1指的是只有一个波束发射和接收，没有使用SAC的情况。轴向和侧向应变的SNR和CNR随着PRF的增大而增大，当PRF达到4 kHz时保持稳定。当PRF＞1 kHz时，使用SAC（NSA=3，5或7）得到的应变的SNR和CNR比没有使用SAC（NSA = 1）的高。当PRF＜1 kHz时，NSA越大，SNR和CNR越低，即NSA=1，3，5，7的SNR和CNR依次变低。而当PRF达到4 kHz后，不同NSA的SNR和CNR则较为接近。

3 讨论

在基于SAC的应变估计中，物体的运动和形变可能会导致运动伪影，而采用合适的成像参数可以减小或避免运动伪影，提高应变估计性能。之前虽然有学者对基于SAC位移和应变估计的最优参数进行了研究[22-22,24,28]，但是据我们所知，目前还缺乏关于其伪影问题的系统研究。本研究通过仿真实验研究了PRF和NSA对SAC运动伪影的影响，并有望在进一步的在体实验验证后提出具有临床指导意义的成像参数，以此来减小SAC的运动伪影，提升颈动脉弹性成像评估易损斑块的性能。

在图4中，NSA=1表现为一条水平直线。这是因为NSA = 1代表只有一个波束发射和接收，没有SAC，即不存在运动伪影，因此SNR和CNR不会随PRF变化。此外，当NSA不变时，使用SAC（即NSA=3，5或7）的SNR和CNR随着PRF增大而增大，在当PRF达到4 kHz后则趋于定值。这是因为物体在多角度发射和接收过程中会产生形变，从而产生伪影。随着PRF增大，每个发射事件之间的间隔时间会缩短，物体在每个发射事件下的形变量也会变小，运动伪影会随着减小，从而应变图像质量会变好，因此SNR和CNR会提高。

当PRF小于1 kHz时，使用SAC的SNR和CNR低于没有使用SAC（即NSA=1）的结果；当PRF达到1 kHz时，趋势开始发生反转。一个合理的推测是，当PRF较小时，SAC的每个发射事件的时间比较长，物体在每个发射事件下的形变量较大，因此使用SAC时的运动伪影较大，而随着PRF逐渐提高，运动伪影的问题才得到补偿。

此外，当PRF小于1 kHz时，角度数量越小时（NSA越小），SNR和CNR越大，随着PRF不断增加，最终不同角度数量的结果接近一致。这是因为当PRF较低时，NSA越大，就会产生越多角度之间的形变，因此使用SAC时的运动伪影越大；当PRF较高时，各角度之间的形变逐渐缩小，最终导致NSA对SNR和CNR的影响逐渐消失。

当PRF＞4 kHz时，NSA为3，5和7的应变结果相似，但在相同PRF下，NSA为3的有效帧频高于NSA为5或7的有效帧频。根据此初步发现，本研究建议将NSA设置为3，可以获得较好的应变估计。考虑到未来应用到商用超声成像系统上时，其存储空间有限，在保证成像质量的前提下，采用较低的PRF可以有效节省存储空间，也可以节省数据传输和处理的时间，本研究建议可获得较好应变估计的最低PRF是4 kHz。

在实际情况中，颈动脉斑块的形变和运动可能更为复杂，因此本研究所提出的方法有其局限性。在仿真实验中，我们设定的压缩方向和大小都是恒定的，然而颈动脉斑块的运动方向和形变可能会随时间变化。因此，在实际的临床应用中，超声数据采集时间不能过长，尽可能避免斑块在采集期间有太多复杂运动。未来我们也会用在体实验对仿真的结论做进一步的验证。