基于大数据的水量监测系统有效性分析

诸葛燕，方海泉

(1.浙江经济职业技术学院，浙江杭州 310018；2.中国航天系统科学与工程研究院，北京 100048)

我国实行最严格水资源管理制度，健全水资源监控体系是实施这一制度的重要举措。国务院《关于实行最严格水资源管理制度的意见》要求，加强取水、排水、入河湖排污口计量监控设施建设。我国各地普遍开展了取用水监测，积累了大量监测数据[1-5]。为了有效发挥取用水监测数据在水资源管理中的作用，需要对监测数据进行整编、清洗、加工，辨识异常数据，保留正常数据，从而对一个地区取用水监测数据的有效性进行评估。

1 取用水监测数据异常值分析

取用水监测数据的有效性评估要以数据真实可靠为基础，为此，首先要对监测数据进行异常值分析，包括监测数据总量、监测数据时序变化两个方面。

1.1 监测数据总量异常

将1 个取用水户同一天所有取水管的监测数据求和，得到该户的日取水量(以下将每个受监测的取用水户简称为“监测点”)；通过计算一段时间的日取水量监测数据，推算出1 年的取水量，即监测年取水量。如果监测年取水量与实际年取水量偏差太大，说明监测数据可能存在异常，包括以下两种情况。

1.1.1 监测年取水量高于实际年取水量

用S1表示1 个监测点的监测年取水量，S2表示该监测点实际年取水量。把监测年取水量除以实际年取水量的比值称为正监测率，记为g.

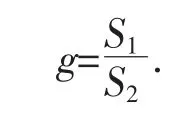
计算出每一个监测点的正监测率得到数组｛gm｝，m 表示监测点的个数。若g 越大，说明监测年取水量高于实际年取水量，则该监测点监测数据异常的可能性就越大。

1.1.2 监测年取水量低于实际年取水量

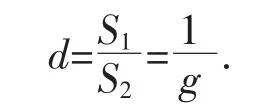
把正监测率的倒数称为倒监测率，记为d.计算出每一个监测点的倒监测率得到数组｛dm｝。若d 越大，说明监测年取水量低于实际年取水量，则该监测点监测数据异常的可能性就越大。d 异常大的一种原因可能是该监测点只监测了部分取水管，还有其它取水管没有监测到，即监测不全面。

1.2 监测数据时序变化异常

对区域内每一个监测点日取水量数据绘制时间序列图，根据图形变化趋势可能存在三类异常值现象：某日数值异常大、某个数据出现频率异常高、某日数据为负值，对每一类异常现象抽象出数学算法，通过MATLAB 编程可以快速、准确分析出每一类异常情况分别存在于哪些监测点。

1.2.1 某日数值异常大

监测点日取水量时间序列数据记为｛an｝，n 表示时间序列的天数，该数组中大于0 的数构成的数组称为正数组，记为｛ank｝，ank＞0，｛ank｝的中位数记为median ｛ank｝，｛an｝的最大值记为max ｛an｝。监测点日取水量时间序列数据的最大值与中位数比值，即最大偏离率，记为。r 越大，则该监测点时间序列数据的最大值为异常值的可能性越大。计算出每一个监测点的r 得到1 个数组｛rm｝。

1.2.2 某个数据出现频率异常高

把时间序列数据｛an｝中每一个不重复的数构成的集合记为，集合中每个数在｛an｝中出现的频率记为P(ant)，该监测点中出现频率最高的数据记为h，P(h)=max(P(ant))(简记为P)，即1 个监测点的最高频率。P 越大，则该监测点监测数据中某个数据出现的频率越高，该监测点数据异常的可能性就越大。计算出每一个监测点的P 得到一个数组｛Pm｝。

1.2.3 某日数据为负值

对于时间序列数据｛an｝，若an＜0，则该日取水量数据为异常值，｛an｝中小于0 的数据的个数记为w，即1 个监测点的负值数，计算出每一个监测点的得到1 个数组｛wm｝。

1.3 异常情况综合分析

对每一个监测点的取用水监测数据，综合考虑监测数据总量和监测数据时序变化两类异常情况，据此建立异常情况综合值的数学模型。

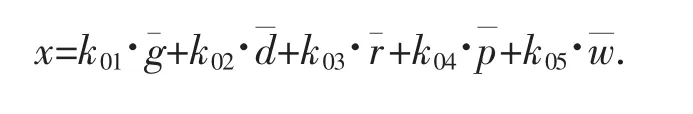
其中k01，k02，k03，k04，k05为权重系数分别为g，d，r，p，w 标准化之后的值。权重系数的确定采用层次分析法中的“两两比较法”[6]。

计算出每一个监测点的异常情况综合值x 得到数组｛xm｝。异常情况综合值x 越大，该监测点监测数据异常的可能性也就越大。采用Grubbs 检验法检验｛xm｝中的异常大值[7]。再进一步判断异常数据是否可以校正，对于单个时间点数据异常大或者出现负值的数据可以采用时间序列预测方法校正异常值[8]，但对于长时间数据异常导致正监测率或者倒监测率异常大的数据是无法校正的。

2 取用水监测数据有效性评估

2.1 有效性评估指标体系

对一个地区的取用水监测数据有效性进行评估，不仅要考察监测数据正常的监测点的数量，而且要考察监测数据正常的监测点所监测水量的大小。因此要建立包括监测点比率、监测覆盖率、监测水量比率的指标体系。

监测点比率y1是指某地区监测点的监测数据经过异常值分析，排除有异常且无法校正的数据，剩下监测数据正常的监测点的个数占该地区有上报监测数据的监测点个数的比例。

监测覆盖率y2是指一个地区监测数据正常的监测点的年监测水量占该地区年取水总量的比例。

监测水量比率y3是指一个地区监测数据正常的监测点的年监测水量占该地区有上报监测数据的监测点年取水量的比例。

本研究所考虑的监测点不包括直流冷却型火电厂监测点。

2.2 有效性评估模型

取用水监测数据有效性评估需要综合考虑监测点比率y1、监测覆盖率y2、监测水量比率y33 个指标，据此建立以下数学模型。

其中k1，k2，k3为属于(0,1)的权重系数，且k1+k2+k3=1，权重系数的确定同样采用层次分析法中的“两两比较法”。由于y1，y2，y3都属于(0,1)，可知z∈（0,1）.z越大，则说明该地区的取用水监测数据越有效。

取用水监测数据经过异常值分析可得到监测数据正常的监测点，为取用水监测数据有效性分析打下基础，监测数据有效性分析建模流程图如图1 所示。

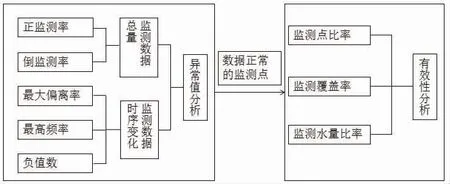
图1 数据有效性分析流程图Fig.1 Flow chart of data validity analysis

3 实例研究

3.1 研究对象

选取G 市的所有监测点的取用水监测数据作为研究对象。G 市有上报监测数据的监测点有27 个。不包括直流冷却型火电厂。

每个监测点的实际年取水量数据难以获取，本研究采用2011 年水利普查时的年取水量(简称水利普查数据)作为实际年取水量，对少部分在2011 年没有被普查到的监测点，采用该监测点的取水许可证许可水量(简称许可证数据)推算出年取水量。理论上，取水许可证的许可水量与实际用水量在统计学上有一定相关性，由此可以根据同时具备水利普查数据与许可证数据的监测点，找到二者的关系，从而推算出没有水利普查数据的监测点在2011 年的取水量，以此作为该监测点的年取水量。这里假定取水户每年的取水量维持在相对稳定的水平，也即假定取水户在2011 年的取水量与2016 年的取水量变化不大。

3.2 监测数据预处理

对于G 市所有的监测数据，整理出每一个监测点的日取水量时间序列数据。考察时间范围从2016 年2 月1 日到2016 年7 月31 日，共计182 d，相当于半年时间，以此半年的取水量的2 倍近似为1 年的监测年取水量。

3.3 监测数据总量异常值分析

3.3.1 监测数据、水利普查数据、许可证数据整理

对于G 市有上报监测数据的27 个监测点，分别计算出每一个监测点半年总用水量S0，进而推算该监测点监测年取水量S1=2S0，监测年取水量列于表1 的第2 列。

根据监测点名称找出对应的水利普查数据和许可证数据。把查找到的水利普查数据和许可证数据分别列于表1 的第3 列和第4 列，其中有4 个监测点没有水利普查数据。

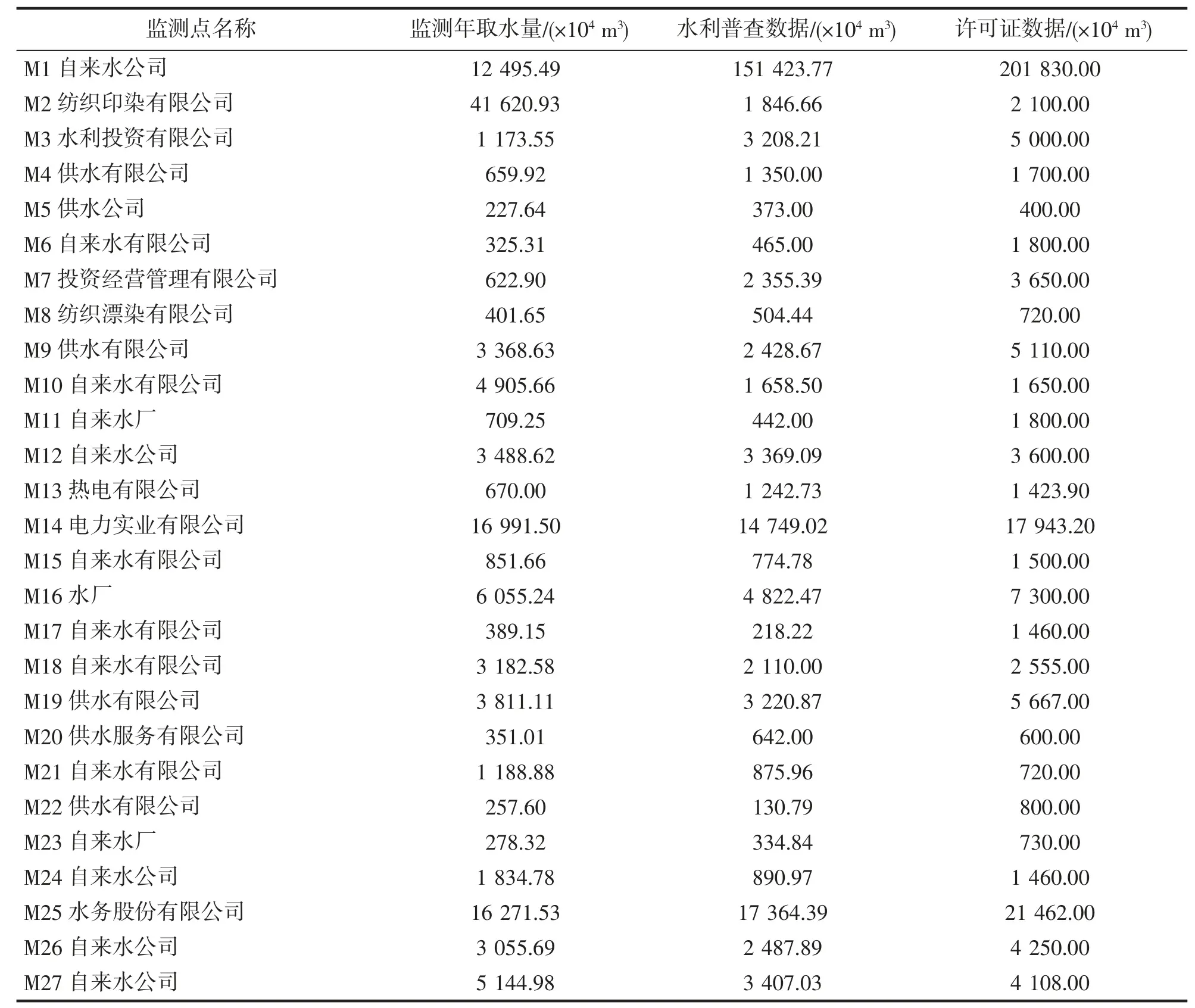
表1 监测点的三类数据Tab.1 Three types of data of monitoring station

3.3.2 用许可证数据拟合出水利普查数据

把水利普查数据和许可证数据都存在的监测点单独列出来，由于数量级差别较大，为了提高拟合准确度，把水利普查数据分为两部分进行拟合，以10 000×104m3为分界点。选出水利普查数据小于10 000×104m3的监测点，计算出水利普查数据与许可证数据的相关系数为0.91，说明二者有较强的相关性。图2 是水利普查数据小于10 000×104m3的监测点的许可证数据与水利普查数据的关系图，直线上的星号是表示根据许可证数据拟合出空缺的水利普查数据。

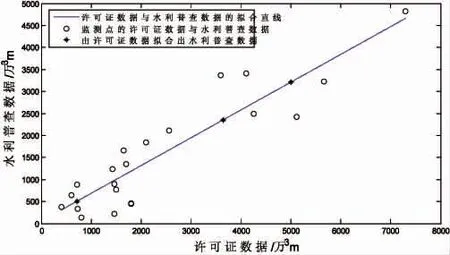
图2 许可证数据与水利普查数据的关系Fig.2 The relationship between license data and census data

同理作出水利普查数据大于10 000×104m3的监测点的许可证数据与水利普查数据的关系图，也可以根据许可证数据拟合出空缺的水利普查数据。表1 第3 列中的加粗字体是表示由许可证数据拟合出的水利普查数据。

3.3.3 计算正监测率和倒监测率

根据表1 的监测年取水量和水利普查数据，计算出G 市27 个监测点的正监测率g 和倒监测率d，计算结果列于表2 的第2 列和第3 列。

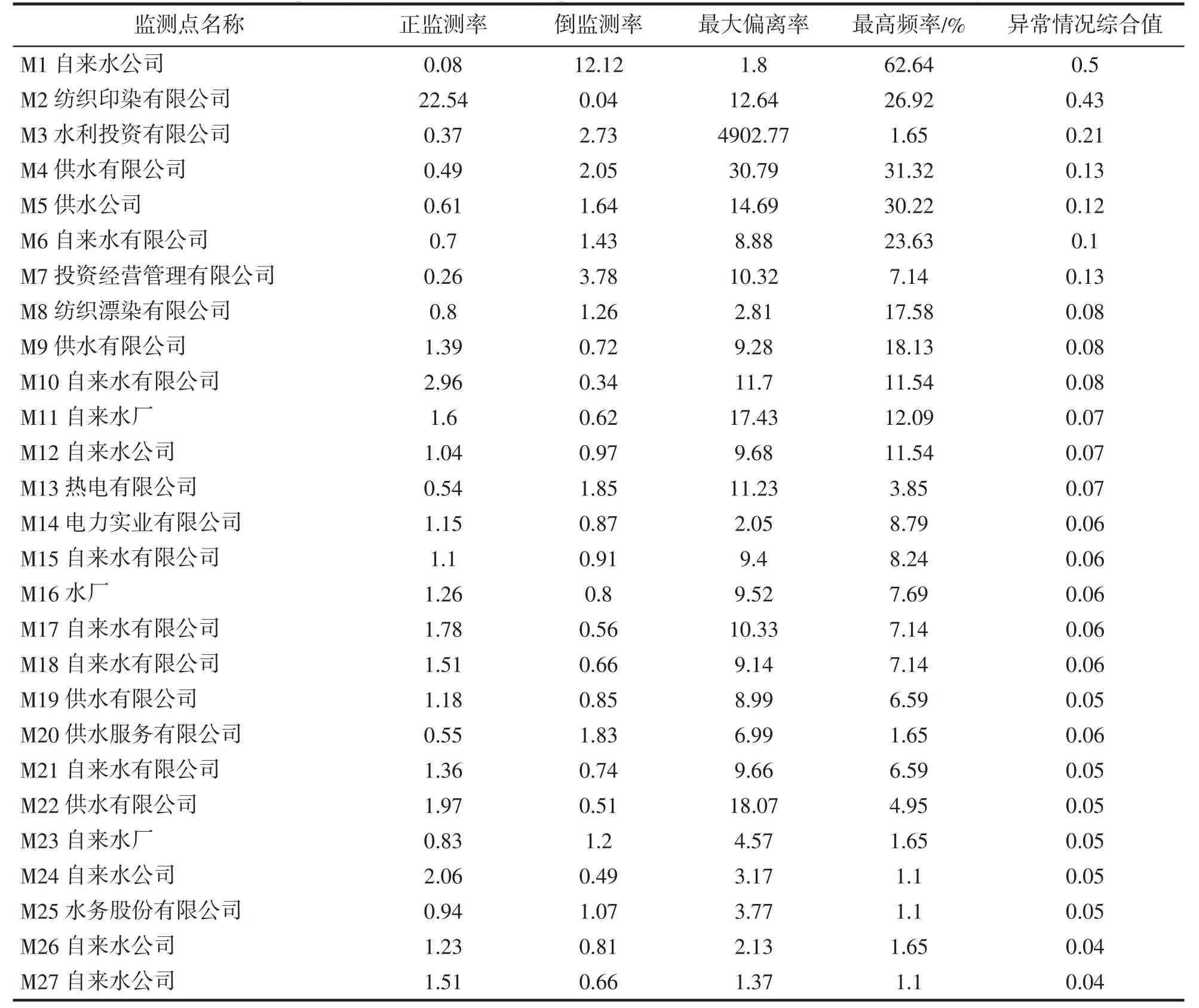
表2 监测数据异常情况的参数值和综合值Tab.2 The parameter value and comprehensive value of abnormal monitoring data

3.4 监测数据时序变化异常值分析

应用MATLAB 编程计算出每个监测点的最大偏离率r、最高频率p、负值数w，结果发现w 都为0，也即该市的监测数据没有出现负值。最大偏离率、最高频率的计算结果列于表2 的第4 列和第5 列.

3.5 计算监测数据异常情况综合值

采用“两两比较法”确定正监测率g、倒监测率d、最大偏离率r、最高频率p 的权重系数，经过咨询水资源专家得到比较矩阵A1.

求出权重系数

经过计算能够通过一致性检验，求得的权重系数可以使用。

综合计算公式如下：

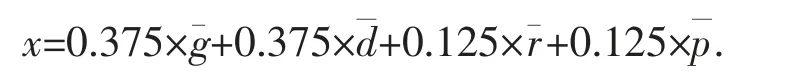
计算出监测点监测数据异常情况综合值x 列于表2 的第6 列，表2 的行排列顺序就是按照x 值从大到小排序的。对x值采用Grubbs 检验得到前3 个监测点监测数据异常情况综合值为异常大值，可初步判断这3 个监测点监测数据属于异常。经过分析发现第一个监测点“M1 自来水公司”监测水量过小，实际用水量是监测水量的12 倍多。第二个监测点“M2 纺织印染有限公司”监测水量过大，是实际用水量的22 倍多。第三个监测点“M3 水利投资有限公司”监测数据存在异常大值，如果是单个数据异常大可以校正，但是从该监测点的监测数据时间序列图(图3)可以看出不只是单个数据异常大，该监测点前1 个月的数据较大，后5 个月的数据相对较小，导致总量低于拟合出的水利普查数据。可以确定这3个监测点监测数据属于异常的可能性非常大，并且这3 个监测点的监测数据都无法校正。

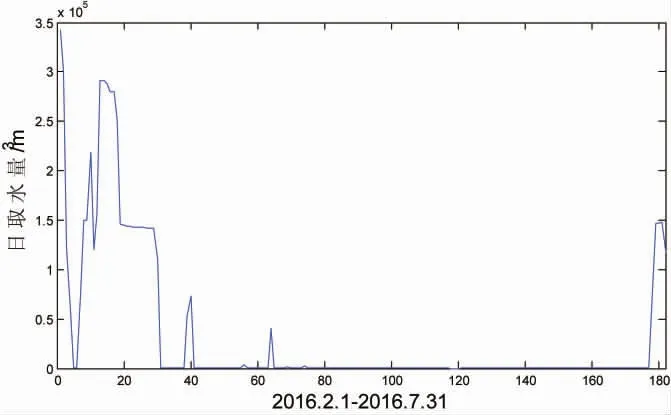
图3 监测数据时序变化图Fig.3 The time series change of monitoring data

3.6 计算监测数据有效性评估值

筛选出数据异常的监测点，从而确定出监测数据正常的监测点，计算出以下三个评价指标值。

3.6.1 监测点比率

对于G 市，排除以上3 个监测数据异常的监测点，还剩下24 监测数据正常的监测点。监测点比率y1=24/27=0.888 9.

3.6.2 监测覆盖率

监测覆盖率y2=7.5043 亿m3/43.45 亿m3=0.172 7.

分子为排除3 个监测数据异常的监测点之后剩下的24 个监测数据正常的监测点监测年水量之和，用表1第2 列后24 个监测点的监测年取水量。分母为G 市2015 年取用水量减去直流式火(核)电用水，该数据来源G 市所在省的2015 年水资源公报。

3.6.3 监测水量比率

监测水量比率y3=7.5043 亿m3/22.2696 亿m3=0.3369.

分子与监测覆盖率的分子一致，分母为G 市27 个有上报监测数据的监测点实际年取水量之和，用表1 第3 列的水利普查数据作为实际年取水量。

3.6.4 取用水监测数据有效性评估

采用“两两比较法”确定y1，y2，y3权重系数，经过咨询水资源专家得到比较矩阵A2.

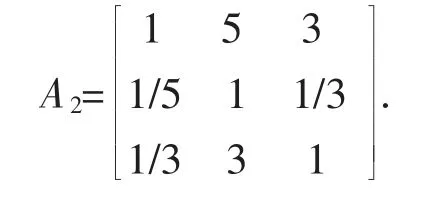
求出权重系数

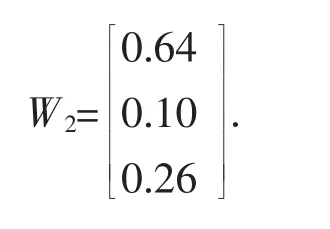
经过计算能够通过一致性检验，求得的权重系数可以使用。

取用水监测数据有效性评估值的计算

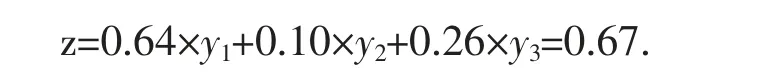
3.7 讨论

已计算出G 市取用水监测数据有效性评估值为0.67，距离理想值1 还有提升空间，若要提高G 市的取用水监测数据的有效性，建议从三个方面加以改进，一是对于监测不全面的监测点要确保监测到所有的取水管；二是对于监测数据大于或小于真实取水量数据的监测点应该检查监测设备以及通讯设施以确保监测数据真实可靠；三是在一定程度上增加监测点数量，并且尽量选择取用水大户进行监测。

4 结论

对一个地区的取用水在线监测数据从数据的总量和时序变化两个方面进行异常值分析，能够有效筛选出异常监测数据。进一步对取用水在线监测数据进行有效性评估，评估结果从一定程度上能够反映出该地区监测数据的质量，从而能够发现存在的问题并有针对性地改进，为取用水在线监测数据服务于水资源管理业务提供更加可靠的保障，也可以为将来智慧水利、智慧流域的监测点建设提供借鉴[9-11]。