FMS偏航距试飞评估方法研究

万振塬 张少莉 黄雪妮

（中国飞行试验研究院，西安 710089）

1 引言

偏航距的定义为飞机当前位置和应飞航迹之间的最短距离，是对飞行管理系统（FMS）导航性能的直接评价。FMS会对飞机偏航距进行实时计算，其计算精度直接影响飞行引导和自动飞行控制，进而影响飞行安全。在目前世界上广泛使用的区域导航（RNAV）、基于性能的导航方式（PBN）及未来空中航行系统（FAN）中，偏航距的计算都是其最为基础且最为关键的一环。

鉴于此，对FMS偏航距的试飞评估就显得尤为重要。偏航距的试飞评估思路为：采用飞机上加装的GPS做飞行后差分处理得到飞机实飞航迹；结合FMS飞行计划中的航段数据——应飞航迹，求出实际偏航距；最后与FMS计算的偏航距进行对比评估。

实际偏航距计算的难点在于确定航线所采用的模型，航空航海领域主要采用的航线模型为等角航线和大圆航线。等角航线在航空技术发展初期或短距离航行时较为常用，随着技术的进步，对经济性、远距离航行等的要求越来越高，大圆航线逐渐成为主要航线模型。相关学者对两种航线模型的总航程（经济性）展开过深入研究，但基于两种模型的偏航距试飞评估方法却鲜有涉及。本文首先推导了两种航线模型下偏航距的计算方法，并设计完成了相应的飞行试验验证，分别采用两种算法求出实飞偏航距，并与FMS计算的偏航距进行对比评估，最后分析两种评估算法的合理性与正确性。

2 基于等角航线的偏航距计算模型

等角航线又被称为墨卡托航线，等角航线在墨卡托投影图中是一条直线段，直线段与正北的夹角为等角航线角，即为该航段的计划航向。

2.1 墨卡托投影

墨卡托投影又称为“等角正轴圆柱”投影，由荷兰地图学家墨卡托于1569年提出，其基本原理是假设有一个在赤道与地球相切的圆柱体，先把椭球面映射到圆柱体表面，然后展开圆柱面，即实现了球平转换。该投影具有等角特性，在保证对象的形状不会改变的同时，也保证了方向和相互位置的正确性，因此常常应用在航海和航空领域。

2.2 等角航线偏航距计算

基于墨卡托投影原理和航线角相等的前提，计算等角航线角和偏航距的公式可通过分段积分的方法导出。如图1所示，设飞行计划某直飞航段上一航路点为 A(φA,λA,hA)，当前航路点为 B (φB,λB,hB)，AB 航段与经度的夹角为θ，距离为S，如果在其间任意取一段很小的航段dS，则该航段与相应的纬度、经度(dφ,dλ cosφ)构成一个近似平面直角三角形，由此可得：

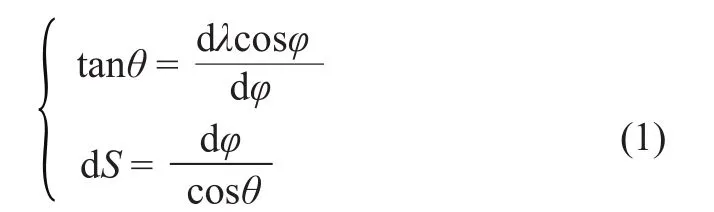
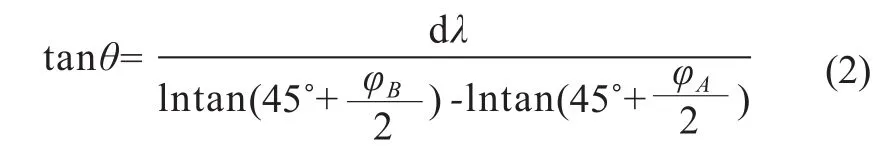
若飞机实际位置为D，在AB航段上找出一点C，使之与D点纬度相同，即可根据下式求得C点的经度，公式如下：

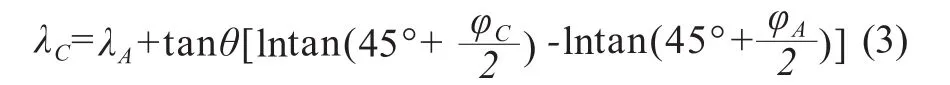
最后，根据球面三角公式可求得等角航线偏航距如下：

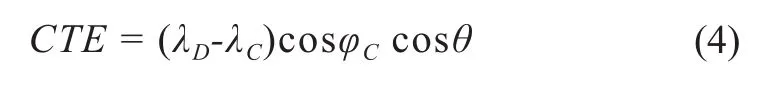
图1 等角航线示意图

3 基于大圆航线的偏航距计算模型

美国航空无线电公司制定的ARINC 424中，对飞行管理系统应飞航迹中的航段设计给出了建议模型，即大圆模型。一般情况下，球面被经过球心的平面截得的圆叫做大圆，被不经过球心的平面截得的圆叫做小圆。球面上两点之间的最短距离就是经过两点的大圆在这两点间的一段劣弧的长度，这个弧长叫做两点的球面距离。航海航空领域也常常沿着这个圆弧航线航行，这条航线就叫做大圆航线(Great Circle)，也叫做经济航线。特别是在高纬度地区，航向接近东西、横跨经差较大时，大圆航线航程比等角航线航程要短很多。

3.1 坐标系

鉴于我们选择差分GPS作为偏航距的评估基准，而目前GPS定位所得出的结果都基于WGS-84坐标系(World Geodetic System，1984年)系统。因此，选取WGS-84坐标来描述基准大圆航迹。WGS-84坐标系的几何定义是：原点在地球质心，Z轴指向地球北极方向，X轴指向零子午面和赤道的交点，Y轴与Z轴、X轴构成右手坐标系。

为了便于建立大圆航线的数学模型并进行运算，本文将WGS-84坐标转化为空间直角坐标。这两种坐标之间的转换关系可由下式得到：

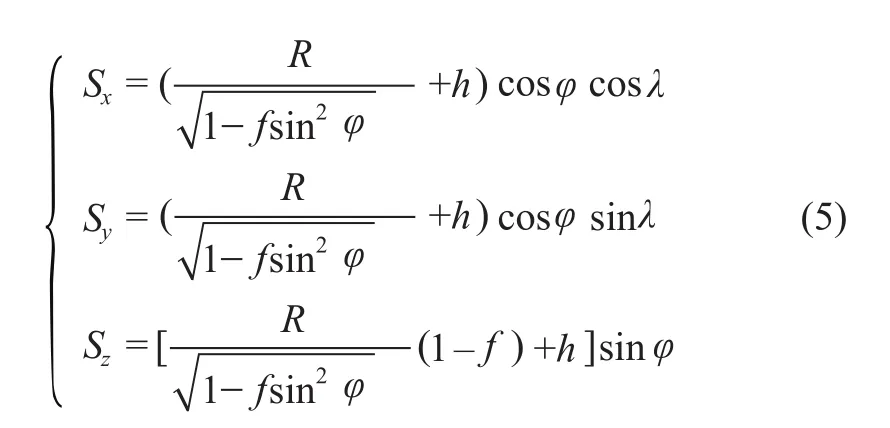
式中，(Sx,Sy,Sz)为空间直角坐标系坐标； (φ,λ,h)为WGS-84坐标坐标（纬度、经度、高度）；R为WGS-84椭球长半轴，本文取6378km；f为WGS-84坐标系的第一偏心率平方。

3.2 大圆航线偏航距计算

设飞行计划某直飞航段上一航路点为A(φA,λA,hA)，当前航路点为B(φB,λB,hB)。则从A到B的基准大圆航迹是过A、B、O(地心)三点的平面与地球椭球面的交线。AB航段大圆航线如图2所示。

图2 大圆航线示意图

空间直角坐标系下，过A、B、O三点的平面方程可以表示为：

将A、B点WGS-84坐标通过式（5）转换为直角坐标(XA,YA,ZA)，(XB,YB,ZB)，并带入式（6）得：

这样，即可获得平面ABO的法向量为N= (a,b,-1)；若此时飞机实际位置为D点（差分GPS提供），转换到直角坐标系下的坐标为(XD,YD,ZD)。此时的偏航距即为D点到平面ABO的垂线DD'的长度，且有DD'//N。根据空间两直线夹角的计算公式可知：

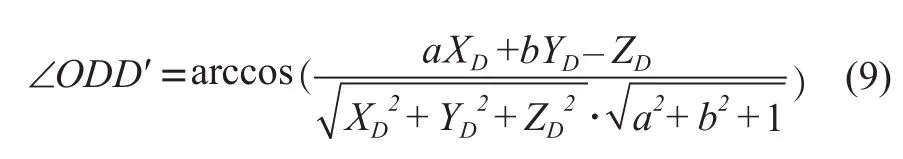
求出两直线夹角并带入下式，即可求得基于大圆航线模型的偏航距：

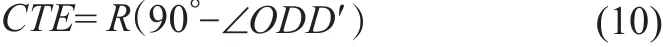
式中，R为地球平均半径，本文取6371km。

4 试飞评估及数据分析

4.1 飞行试验

4.1.1 试飞方案设计

为验证飞行管理系统偏航距试飞评估方法的正确性，在某型试验用运输机上装载的国产飞行管理系统中，加装测试用GPS，在飞行管理系统中加载或创建飞行计划，如表1所示。试飞员选择“惯性/卫星”作为飞管导航源，接通自动驾驶模式（AP）以排除飞行技术带来的误差（FTE），接通水平导航、垂直导航和自动油门，并激活飞行计划，最后按照计划完成飞行试验。

试飞过程中，一方面，该飞行管理系统会依据自身的导航系统实时给出当前飞机的偏航距，此偏航距反映了设计单位对偏航距计算模型的选取思路；另一方面，基于加装的GPS做飞行后差分处理，依据本文推导的基于等角航线和大圆航线的计算模型计算出飞机实际偏航距。最后，将三者做对比分析。

表1 飞行计划

4.1.2 试飞飞机条件

试飞飞机要求具备以下条件：

（1）试验用某型国产运输机；

（2）机载自动飞控系统：与飞行管理系统交联，支持其自动驾驶功能；

（3）机载飞行管理系统：具备自动驾驶、自动油门水平导航及垂直导航功能，可实时计算输出飞机位置、速度、轨迹角、偏航距、偏航角、轨迹偏差和剩余飞行时间/燃油等参数；

（4）导航系统：加装测试用GPS；另外，偏航距的评估与机载导航系统性能密切相关，表2给出了飞行试验涉及的机载导航传感器精度。

表2 导航传感器精度

4.1.3 试飞实施

2018年7～9月，在某军用机场按照上述飞行计划组织完成4个架次的飞行试验。本文详细介绍了2018年7月第1架次试飞情况，实际飞行轨迹如图3所示。

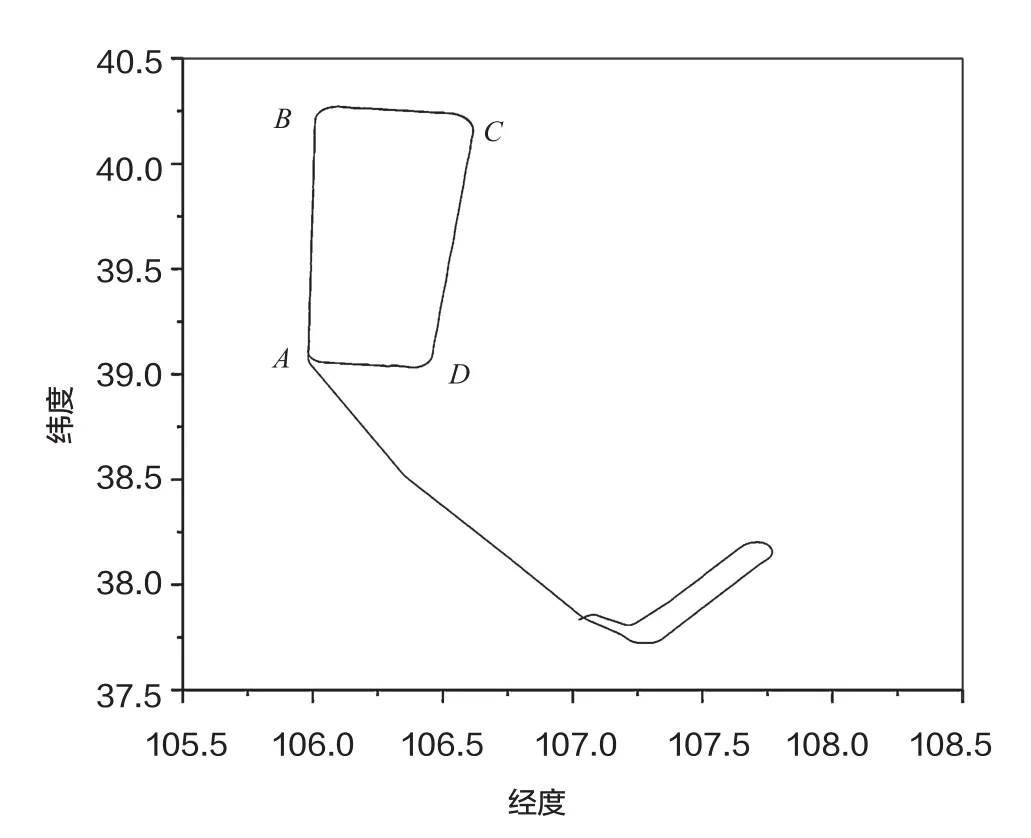
图3 飞行轨迹

4.2 试飞结果与数据分析

取2018年7月第1架次AB（南北方向）和BC（东西方向）两个航段的试飞数据，分别采用大圆模型（MODEL1）和等角航线模型（MODEL2）进行偏航距计算，并将计算结果与飞行管理系统输出的基准偏航距作对比，偏航距试飞结果如图4所示。采用上述2种模型计算4个飞行架次的偏航距，并统计偏航距的95%圆概率误差，试飞结果见表3。

表3 偏航距试飞结果统计（95%CEP） （nm）

分析偏航距的时间历程曲线，结合偏航距统计结果可知，基于大圆航线模型的偏航距与FMS计算偏航距的时间历程曲线更加契合，且精确度更高。与设计单位沟通，印证了大圆航线评估模型的合理性，可作为RNAV/PBN评估的标准算法。

需要说明的是，由于试飞评估计算偏航距与FMS实时计算偏航距采用的导航基准不同，两者之间仍存在一定误差，但此误差也反映出FMS偏航距的计算精度。

5 结束语

偏航距的实时计算是飞行管理系统的一项重要功能，是实现RNAV、PBN及FAN的关键技术。偏航距评估模型选取不当，将无法有效验证FMS偏航距计算的准确性，从而直接影响到导航精度甚至是飞行安全。本文介绍了等角航线模型，着重推导了大圆航线模型的偏航距计算方法，并通过飞行试验验证，确定了基于大圆航线模型的偏航距试飞评估方法的正确性与合理性，为后续RNAV和PBN试飞奠定了理论基础。