一种用于三维重建的多视图前景目标自动分割算法
2019-06-17朱正伟
朱正伟 张 静 饶 鹏 陈 忻
1(常州大学 江苏 常州 213164)2(中国科学院上海技术物理研究所 上海 200083)
0 引 言
多视图前景目标分割是指从来自不同视点的多个图像中分割前景对象,其在计算机视觉中有着重要应用。在多视图立体视觉中,为了减小时间成本,三维重建的第一步通常就是对前景目标进行精确提取。另外,前景目标分割也是目标跟踪的重要步骤。
在多视图中分割前景目标最简单的方法是单独处理每幅图像,分别分割出前景目标。一般来讲,这类方法[1-3]需要通过用户交互来获取如每个前景目标的边界框或前、背景涂鸦等初始输入。而基于图像的三维重建往往需要大量的图像,大量对图像进行分割是对人力的浪费。
用于三维重建的多视图图像具有相同的前景对象,因此考虑利用不同输入图像之间颜色、纹理、形状等外观属性的统计相似性,采用协同分割的思想进行多视图图像前景目标的分割[4]。Rother等[5]提出了一种基于马尔科夫随机场(MRF)的能量模型,并在模型中加入匹配公共部分的外观直方图的全局约束,通过TRGC优化对模型近似求解来实现多图像前景目标协同分割。Mukherjee等[6]建立了类似于文献[4]的能量模型,但与其不同的是,Mukherjee等通过二范式来衡量前景直方图之间的差异,并采用二次伪布尔优化来近似求解分割结果。与文献[5-6]的惩罚模型不同,Hochbaum等[7]建立了奖励模型。Vicente等[8]将能量函数进行了优化,优化后的函数包含平滑项和全局约束,并提出了基于Boyov-Jolly模型的扩展模型。然而,这些方法仅在分辨率相对较低的图像中进行粗略分割,且分割边界也不够精细,分割出的前景目标不能满足三维重建的需求。此外,文献[6-7]仍需根据用户交互建立先验模型。因此,本文在先前的方法基础上进行了改进,实现多视图前景目标自动分割。
前景目标分割及重建方法步骤如下:
Step1对输入图像进行颜色、几何一致性测量;
Step2构建基于MRF的能量函数;
Step3利用Graph Cut迭代求解能量函数,得到第一次分割结果;
Step4KL散度检测颜色混合区域;
Step5对颜色混合区域使用Matting细化边界,得到第二次分割结果;
Step6将精细分割后的多视图照片用于三维重建得到前景物体三维模型。
本文算法大致可分为三个阶段,首先通过对图像进行颜色、几何一致性分析,确定前景目标所在区域。然后构建能量方程,方程的数据项使用多个输入图像上的颜色和几何一致性来定义的似然相似度,平滑项使用在每个输入图像中单独定义的图像的局部结构。之后利用Graph Cut算法迭代地更新颜色和几何测量值,初步实现前景目标分割。为了使分割更加贴近物体边界,本文引入第二阶段算法对分割结果进一步细化,通过评估局部像素带内的颜色分步来确定前景背景颜色混合的未知区域,并使用Matting细化前景对象的分割边界,得到高质量的分割结果。算法的第三阶段将以上分割的结果用于三维物体重建,以此提高三维重建的速度。本文算法在多图像分割上避免了大量的人工交互,能够自动从多视图图像中分割出前景目标,即使对于高分辨率图像,本文算法仍能获得良好的分割边缘。将该算法用于三维重建的前期图像处理,可大大提高三维重建的速度。
1 多视图对象分割
1.1 颜色模型
本文用高斯混合模型GMM为每个图像的前景和背景颜色分布构建颜色模型,并根据颜色模型计算某像素点属于前景和背景的可能性。此外,在构建GMM之前先使用双边滤波去除图像噪声及微小细节,避免颜色分布的过度拟合。本文的高斯混合模型包括前景GMM和背景GMM,定义如下:
(1)
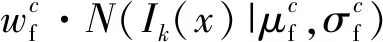
1.2 几何模型
为了实现所有视图中一致前景目标的分割,本文假设在所有不同视点前景对象都完全位于摄像机视野范围内。对于输入的多视图图像的每个视点,通过检查点在图像上的投影是否在当前的前景二值分割范围内,可以投票给假设点H(x)。为了测量前景的几何一致性,本文使用S型函数(Sigmoid Function)定义如下所示的几何模型:
(2)
式中:sk(x)=max(pk(H(x)))是投票最高得分,K是输入图像的数量,参数λ用于控制能量函数形状,在本文中λ=20。若投票最高得分sk(x)小于K,则认为此像素几何不一致。
1.3 MRF能量方程的构造与求解
1.3.1MRF能量方程的构造
第一阶段的分割目标是在多视图图像I={I1,I2,…,In}中,估计前景目标的二值掩码图像X={X1,X2,…,Xn},其中n表示输入图像的数量。在MRF框架中,此阶段的分割可被表述为单一能量函数[9]。在先前研究的基础上,本文构造了如下能量方程:
E=λEd+En
(3)
式中:Ed为能量方程的数据项,Ed=ρ(x)Ec+(1-ρ(x))·Eg。En为能量方程的平滑项,En=λnc·Enc+λng·Eng。与先前研究不同的是,本文能量方程的数据项包括颜色模型Ec和几何模型Eg。对颜色模型中概率取负对数,可将最大后验概率估计问题转换为MRF框架中的能量最小化问题。
数据项中参数ρ表示权重,用来平衡颜色和几何一致性。
(4)
像素颜色与前景GMM和背景GMM距离接近时,相应减小颜色模型的权重,同时增加几何模型的权重。P(Ik(x)|Gf表示像素Ik(x)是前景Gf的概率。
平滑项用来主要体现相邻像素之间不连续的惩罚,本文使用颜色能量Enc和几何能量Eng定义两个相邻节点xp和xq的能量,如式(5)、式(6)所示:
Enc(xp,xq)=∑p,q|xp,xq|·exp[-β(Ip(x)-Iq(x))2]
(5)
(6)
式中:参数β由图像的对比度决定,图像本身对比度越低,β值越大,enb表示背景能量。
1.3.2MRF能量方程的求解
本文使用图割(Graph Cut)算法对式(3)中的能量方程进行求解,以此得到第一阶段二值分割的结果。在Graph Cut中,图像的分割可以看作像素标记问题,本文将前景目标和背景的标签分别设为1和0,将最小化图割问题转换为最小化能量方程问题,从而实现前景目标和背景的分割。
Graph Cut分割原理如图1所示。首先使用无向图表示要分割的图像,Graph Cut图包括普通顶点和两个终端顶点,顶点具体对应输入图像的每个像素,图中连接两个相邻顶点的线叫做边,每条边都有非负的权值,在图割中可以权值可以理解为分割代价。图割的目标就是求解令边的权值之和最小时得最小割(min cut)。由于最小割等价与网络的最大流,因此本文采用文献[10]的方法最小化能量方程,迭代地对能量方程进行求解,直至E收敛。

图1 Graph Cut分割示意图
2 Matting边缘优化
第一阶段通过使用Graph Cut迭代地求解能量函数,得到初步分割结果。若将分割结果直接用于三维重建,相对粗糙的边缘会降低三维模型的完整度,因此引入第二阶段过程,使用Matting[11]将部分前景目标分割边缘进一步优化。
2.1 模糊边界检测
首先检测第一阶段分割边缘中模糊的边界,也就是前景和背景不确定的区域。本文使用局部边界区域中的KL散度(Kullback-Leibler divergence)衡量前景-背景的不确定程度。局部颜色混合的效果近似于两种不同颜色的线性组合[12],因此使用线性模型衡量局部颜色分步的KL散度,公式如下:
(7)

沿第一阶段分割的边界均匀地采样种子点,并使用上述线性模型衡量每个种子点局部颜色分部的KL散度。边界清晰附近的区域,颜色样本集中在线性模型的两端,而边界模糊的区域,颜色样本的分布会集中在线性模型的中间。通过找到投影颜色靠近局部线性模型中间的像素,可以检测出第一阶段分割结果中前景—背景不确定区域。
2.2 边界优化
为了能得到更精细的分割结果,同时提高计算效率,仅对第一阶段分割结果中前景-背景不确定区域使用Matting进行边缘优化,求解alpha matte的目标函数:
a*=arg minααTLα+λ1(α-αg)T(α-αg)+
λ2(α-αb)TW(α-αb)
(8)
式中:L是Matting拉普拉斯矩阵;αg是第一阶段分割结果;αb是边界像素的约束;W是对角矩阵,如果像素是边界像素,则其输入等于1,否则为0;λ1、λ2是平衡两个约束的权重。
3 三维重建
考虑到重建成本和通用性问题,本文选取更常见的普通相机,从多视图图像中恢复物体三维结构。三维重建方法步骤如下:
Step1SIFT算法进行特征点检测;
Step2SIFT算法完成特征点之间的匹配;
Step3SFM技术得到稀疏点云;
Step4通过CMVS获得稠密点云;
Step5MeshLab软件生成物体三维模型。
将分割后的多视图图像序列作为三维重建的输入,首先使用SIFT[13]检测特征点,并在不同图像之间进行特征点的匹配。然后利用SFM技术建立三维物体的稀疏点云,稠密点云则通过将稀疏点云输入CMVS[14]获得,最后使用MeshLab软件生成物体三维模型。
4 结果及分析
为了验证分割算法的有效性及其对重建结果的影响,本文首先进行了数据的采集。数据采集使用一台相机环绕物体拍摄得到。本文所用相机的型号是(索尼ILCE-7RM2),镜头型号SEL50F18,焦距50 mm,拍摄角度差值约20°。在无遮挡的情况下拍摄示意图如图2所示。每组数据由20张尺寸为1 200×800的图像组成。

图2 拍摄示意图
为了说明分割算法的效果及不同分割算法对三维重建的影响,本文在采集的数据上进行了测试,并将无图像分割、利用Grab Cut算法分割以及使用本文分割算法的多视图图像及三维重建结果进行了定性与定量的比较。其中,图3、图4是对室内物体和室外物体进行数据采集、自动分割的结果,从左到右分别为原图、Grab Cut分割结果、本文分割结果。结果显示,在前景后景颜色分布较为接近时,单纯依靠Grab Cut算法难以得到良好的分割边缘,而本文的分割算法能在无需人工交互的前提下自动分割得到完整的前景目标。

(a) 原图 (b) Grab Cut分割 (c) 本文分割图3 室内物体分割结果

(a) 原图 (b) Grab Cut分割 (c) 本文分割图4 室外物体分割结果
图5展示了对无分割、Grab Cut方法分割、本文算法分割后的多视图图像进行三维重建的结果。由于Grab Cut算法在分割时损失了一部分的边缘信息,导致三维重建结果不够完整。

(a) 原图 (b) Grab Cut分割 (c) 本文分割图5 采用不同方法分割后三维重建结果
为了进一步评价本文算法,将一组照片不分割、Grab Cut算法、本文算法分割的分割和重建总时间进行了对比,对比结果如表1所示。对于单幅图像分割,Grab Cut平均需要14.26 s,而本文算法平均需要12.00 s;不对图像进行任何分割,直接进行三维重建需要耗时12 652.47 s,使用Grab Cut分割后再重建需4 915.59 s,本文算法分割后重建需5 568.76 s。本文算法分割后重建时间更长是由于其边缘完整,保留了更多的特征点,在重建结果上也可清晰地看到本文算法分割后重建结果大幅度优于Grab Cut分割再重建的结果。

表1 分割和重建消耗时间对比 s
5 结 语
图像分割作为图像处理的基础,在计算机视觉领域有着不可忽视的作用。如仍采用人工交互方式进行多视图图像的前景目标分割,过程过于繁琐且浪费人力。本文提出一种用于三维重建的前景目标自动分割算法,首先根据图像序列的颜色一致性和几何一致性,确定前景后景大致区域,并以此构建能量方程,用Graph Cut求解能量方程得到粗略分割结果;然后使用Matting细化分割边界,得到高质量的分割结果;最后使用分割后图片重建出物体三维模型。实验表明,本文提出的分割算法速度快、分割质量高、无需人工交互,将本文分割算法用于三维重建前期图像处理,可在大幅度缩短三维重建时间的同时,获得与不分割时精度相当的三维模型。
今后的研究将考虑将多视图图像前景自动分割和物体三维重建集成在同一程序内,实现自动的基于序列图像的物体三维重建。
