一种基于非平滑特征的简化实景网格评价方法

刘盛恩 薛俊诗 易 辉

(航天工程大学研究生院 北京 101416)

0 引 言

倾斜摄影建模是机器视觉的重要应用之一，可以低成本地实现智慧城市三维架构的构建，并且相对于激光雷达可以较为容易地贴上纹理，使得建模的浸入感真实感强，但精度不足。一方面存在透视失真、遮挡[1]，另一方面机器视觉是通过根据像素分布和亮度、颜色等信息抽取目标的位置信息[2]，而且UDSM存在大量理论上的平整且纹理相似的表面如墙面、屋顶、道路，像素之间的信息分辨度低，容易造成误差。真实情况中这些表面可以认为是完全平整的，所以理论上对这些位置的简化三角面应当越少越好[3]。但是在建模得到的网格中，建筑的平整表面并非完全平整，所以这就带来两个问题：一是比较平整表面与原网格差异的大小来评价网格简化算法不客观；二是无法定量验证平整表面网格少的情况下简化其他细节的简化精度，如文献[3]就没有定量验证。

网格定量评价研究主要针对网格差异和网格平滑两个要素，Metro简化网格对照工具[4]至今是评价简化算法误差的主要量化标准，通过蒙特卡洛采样将网格距离简化为可以计算的点面距离。为了解决Metro工具忽视视觉真实感的问题，文献[5]利用二次误差矩阵(QEM)计算误差，文献[6]提出单个三角网的质量标准，文献[7]进一步对顶点的平整度、平滑度、偏差度和形状进行量化。很多研究常常将模型平滑度作为网格质量的标准，包括研究曲率矩阵的奇点[8]、网格结构失真测度(MSDM)[9]和高斯曲率[10]等，这些方法都基于模型的平滑特性。但是UDSM的曲率变化剧烈，导致一些三角边对应的二面角变化很大，也就是突变成为了必然，这就是这里说的非平滑特征。利用UDSM这个重要特征，可将其分类为平整网格表面和细节网格表面。

尽管Metro不能体现算法保持原网格细节的能力，但Metro因其对模型和简化算法没有先验要求，所以网格简化研究一般采用Metro工具进行测量与原网格的差异。文献[11-12]回避了与经典并且Metro测量结果较好的QSlim[13]算法进行比较。以斯坦福兔子作为案例进行研究时，原模型三角面片数量通常为70 k如文献[11]，而在文献[12]中顶点数量就达到了219 k，展示Metro测量结果时压缩了实际简化率。文献[14]的室内网格与UDSM有类似特征，但在加强拓扑保真度的同时Metro测量结果仍然不如QSlilm。文献[15]的UDSM简化研究中只是对比在极高简化率(>0.99)下的Metro测量结果，虽效果良好但片面性强，不符合多层次细节LOD的要求。上述几种算法简化后模型的视觉效果好于QSlim，但在Metro工具测量误差时没能客观评估视觉效果。

另外有些算法的评估针对特定的算法或者同类算法。文献[16]通过面积和离散曲率加权得到新的二次误差矩阵(QEM)测度方法，但都是通过展示网格来表达简化模型对原模型特征的保持。另外，有些研究利用自身算法的误差测度来衡量简化质量，文献[17]引入平方体积误差，文献[15]引入与代理平面的距离误差，这些都只限于简化算法本身或者同一类的简化算法，缺乏鲁棒性。

提取平整表面网格的方法主要包括随机抽样一致性(RANSAC)算法[18]、霍夫变换[19]和特征阈值[20]，这些研究基于Lidar数据，而且都以模式识别为目的，文献[21]采用水平和竖直法向量对倾斜摄影数据进行分类，不能覆盖所有平整表面。其中特征阈值法识别平整面的精度较高。

本文将顶点、三角边和面片分成平整与细节两类，通过边扩展采样方法测量细节误差，然后均匀平衡地对三维表面进行采样，其中细节区域的采样需要体现建筑框架的精度，因而采用了基于周长的蒙特卡洛采样方法。在此基础上测量两类表面与原网格的误差及平整表面的平整度。

1 平整表面的识别

在倾斜摄影重建的三维模型中，墙面、屋顶和道路占了很大一部分。一方面简化代价最低，具有很大的评估价值；另外一方面，根据机器视觉的原理，特征点匹配往往是灰度微分较大的区域较准，而平整表面常常纹理相似度高，三维重建结果误差大。不过平整表面在一般的航摄相机精度范围内(>0.1 m)可视为完全平整，要对其进行单独研究需要先提取并分类。

1.1 平整顶点识别法

平整表面识别的基本单元一般是三角边和顶点。其中三角边一般以边二面角进行测度，顶点主要是研究目标点和周围点的关系。本文采用的方法是先识别顶点，得到的平整点周围的三角边和面认为是平整的，在这之后利用识别的平整边的特性扩大识别范围。顶点的相邻顶点定义为与其构成三角面的所有顶点，三角面片若平整，则至少有一个顶点或者两条边是平整的。首先进行平整顶点的识别。

(1)

其特征值为λ1、λ2、λ3(λ1≤λ2≤λ3)，根据最小二乘和特征值原理[22]，最小特征值和特征值之和为：

(2)

(3)

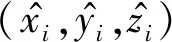
λsum可代表Vp和其邻接顶点覆盖的面积，因此将标准化特征值φ=λ1/λsum作为判断顶点平整度的指标。φ作为平整度指标要好于相邻三角形的夹角。假设一个顶点和与其连接的顶点在投影面上的形成以Vp为圆心，{Xi(i=1,2，…,nv)}形成八个夹角都为45°的标准形状。半径为1 m而假设每个顶点的波动都为0.1 m，则φ的值为0.011，对应围绕顶点每条邻边与最小二乘平面的夹角均值为5.72°，若波动增加到0.2 m，则φ的值为0.045而夹角均值为11.31°。在波动增加一倍时，φ需要增至四倍而夹角只需要增至不到两倍，所以φ作为顶点平整度指标可以更好地提取准平面区域。

确立提取平整表面的标准后，需要找到适合φ的分割阈值εφ，来分离平整表面和细节区域。为了验证抽取方法的鲁棒性，将由82个瓦片构成的大连市某区域的UDSM的顶点进行平整度计算，并统计所有瓦片φ和顶点加权比例的关系，其中顶点Vp的权为以公共顶点为Vp的所有三角面的面积之和，三角面的权为其面积，φ间隔为0.001，φ对应的值落在区间(φ,φ-0.001]的加权顶点比例。计算区间顶点的加权比例需要采用合适的最小统计值Smin，使得得到的不同瓦片的εφ均方根误差最小。由于模型是一次完整航拍和同一个三维重建系统构建出来的，εφ应尽量保持一致。以0.01%作为间隔研究Smin的最佳值，得到当Smin为0.06%时，所有瓦片都拥有除初始零点区间之外的零点区间(φ取值连续为零)，且所有瓦片的εφ均方根误差最小，图1为整个UDSM的统计结果。其中非初始零点区间中最大“窗口”的中点为εφ，εφ落在区间[0.016,0.019]。在判定简化网格的分割阈值εφ时，会出现其他零点区间，此时选择最大的零点区间取中值得到对应的εφ。

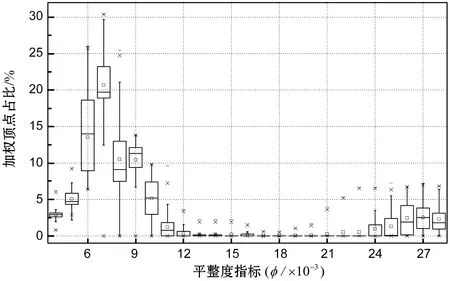
图1 大连某区域UDSM瓦片顶点平整度统计图

1.2 边缘平整网格识别

上节得到平整顶点进而得到平整三角面，基本上排除了非平整区域的偶然误差。而在此识别过程中，有部分三角面只有两条边被识别为平整边缘，另外一条边可能处于平整区域边缘，三个顶点都不平整，此时利用边识别的方式，其二面角的阈值设定为已识别的平整三角边平均值二面角Ad：

(4)

式中：Ue为顶点识别步骤已经识别出的边的总和，n1和n2为边的两个邻接面片的外法向量。此时当三角面片的一条边被识别为平整时，即归类为平整面片。这个步骤不产生新的平整顶点。

2 测量体系的构建

要构建出能测量原网格与简化网格差异的架构，既需要满足网格分类的要求，又要满足分类后分别测量的要求。网格是由面组成的，测量网格的差异就需要转化成数学上可以度量的点面距离，要实现这个转化就需要对采样主体(主网格)进行采样。

传统的三维模型的数据结构(顶点坐标和索引、三角面片对应三个顶点的索引、三角面片的正法向量)不足以支持上述两个步骤的运行。

2.1 基于周长的边扩展采样方法

在UDSM中，建筑结构边缘的三角面大多属于低质量三角面片(正三角形质量最高)，但是建筑边缘又决定了建模的基本架构，重要性高。所以Metro的以面积为权的采样方式不再适用。同时还存在一些三角边，交会的两个面片却都属于平整面片，这些边构造出城市架构：一方面建筑边缘UDSM中最重要的要素——建筑物精确度非常高，而上述的边缘位置是决定建筑位置信息的重要元素；另一方面由于光照造成部分镜面反射，造成边缘位置与周围的区域像素区分度高，因而倾斜摄影建模精度高，需提高这种细节的权，即提高采样率。为了保证采样测距足够准确和稳定，引入基于周长的边扩展采样方法。

在细节表面中，城市架构边缘主要由低质量的三角形和纯粹的边缘构成，如图2所示。

图2 城市架构边缘示例图

图2中的光线与下侧的平整表面垂直，可以看到边缘的三角网质量比较低。而其他细节(如树冠)存在较多高质量的三角形。所以为了能增加城市架构的权，以三角形的周长而不是Metro的面积为权，对三角面片进行蒙特卡洛采样。

对于两侧都是平整三角面片的三角边，需要对其进行虚拟三角化，将这种三角边视为周长为其两倍的三角面片，周长加权采样时，某虚拟三角边的采样点数量为Nspl时，采样位置为该边的Nspl分位点。

平整表面的采样方法，与Metro相同。

2.2 基于周长的边扩展采样方法

根据以上分析，本文算法流程如下：

构建顶点(Vertex)、三角边(Line)和三角面(Face)的数据结构，许多格式如obj三角面片本身就包含三个顶点的索引或者坐标和单位法向量，利用这个数据构建数据结构。

structure Vertex:

{ float pos[3];

Vertex(&Neivertex)[m];

float

float planarity;

float weight

bool sort;}

structure Line:

{ Vertex(&vertex)[2];

Face(&face)[2];

float angle;

bool sort;}

structure Face:

{ Vertex(&vertex)[3];

Line(&line)[3];

float normal[3];

float area;

float weight;

bool sort;}

其中边索引是大部分三维模型格式不具备的，需要根据面结构进行重构。并且三个几何结构都有一个负责分类的bool类型，以记录点线面是否平整。三角顶点与通过三角边连接的邻点的坐标进行计算，得到平整度参数，最后通过整体运算得到顶点的分类——平整顶点或细节顶点。分类步骤所需要的顶点的权则通过面片索引得到，面片的权则通过面积和所有面片的面积得到。

线的分类是否为需要边扩展成虚拟三角面，这个在细节误差测量中非常关键。而所形成的条件为必须两个端点为非平整而相邻平面都平整，所以需要顶点和面片索引各两个。

3 测量值及评估参数

通过上一节的采样方法，将原网格视为主网格，所有采样点与简化网格的距离借助POV ray-tracer[23]中的高效方法进行测度，在此基础上，计算两个部分的平均误差和均方根误差。将UDSM原网格分成两类之后，分别将其与原网格进行对照。评估参数如下：

平整表面平整度：当识别结束后，更新平整三角边的总数Ue和对应平整表面中内部的三角边(不包括单个连通域的边界)两侧面片的单位法向量，得到评价的其中一个指标——表面平整度：

(5)

本质上是平整三角边二面角的平均值归一化的结果，相对于文献[7]定义边平整度的方法，这里定义的ξp与实际的边夹角完全的正比例关系，不会受到余弦函数斜率不均匀的干扰。

平整表面平均误差ξm和均方根误差ξRMS：该指标是简化后的平整区域与原网格的平均误差。一方面虽然原模型存在平整表面误差，平整表面简化到一定程度理论上不会继续增大，若出现突变，简化网格结构必然没能保持好。

其他细节表面平均误差ϑm和均方根误差ϑRMS：细节上特征的保持是所有网格简化的重点，UDSM也不例外。这些区域的误差才是UDSM简化更加需要保持精度的部分。

上述参数的评估方法都是通过改变Metro主网格采样的对象得到的，这里的主网格固定为原网格，非主网格就是简化网格。一方面由于这个方向的误差评价精细，比反向误差要大，而且一般网格对比时取较大误差。另一方面简化后的网格细节表面的位置会发生很大的变化，图3对比了QSlim[21]简化90%前后细节表面的识别效果。

(a) 简化前的细节识别效果

(b) QSlim简化后的细节识别效果图3 网格简化前后细节非对称性示例图

图3中的灰度值大的面片为细节表面，灰度值小的面片为平整表面。由图可知原网格和简化网格的分类差异大，无法对应，所以误差双向比较没有意义。一方面研究的目的是评估UDSM原表面网格的细节简化效果，所以将原网格视为主网格来进行评估；另一方面误差一般取较大值，由于原网格较为精细，除了异常情况，原网格到简化网格的距离往往大于简化网格到原网格的距离。

4 实验结果和讨论

为验证评估方法的性能，采用Visual Studio 2015平台和VTK库，对比分析所用的软件是Metro4.07，计算机配置为Intel Core i5 CPU, 2.6 GHz，内存为8 GB，对三种不同的二次误差矩阵边折叠网格简化算法进行评估，对比的三个简化方法为QSlim算法、面积加权的QEM方法(aQSlim)和体积平方的度量方法(vQSlim)。实验中用Metro测量这三种简化方法与原网格的误差时，最优替换法的结果比子集替换法更为接近，所以不同于文献[3]采用子集替换法进行半边折叠，本文采用最优替换法进行实验，简化比从微小的0.2至较高简化比0.95，提升对评估方法精度的要求。

对选取的瓦片(v:55816;f:109936;diag:166.03)使用Metro测量三种简化算法的均值误差和均方误差，如图4所示。

(a)

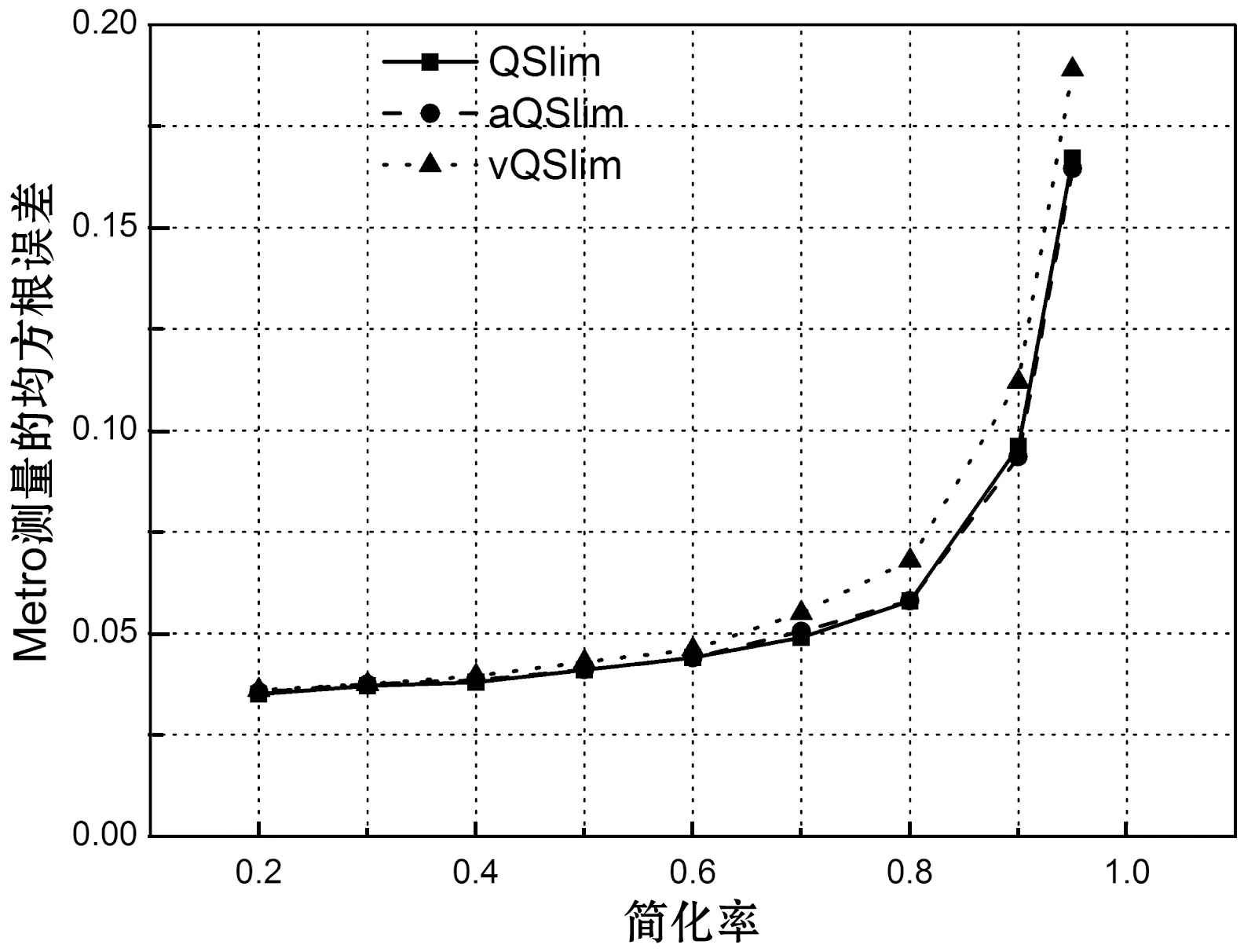
(b)图4 Metro测量结果

Metro测量的平均误差和均方根误差可以辨别vQSlim法比其他两种简化方法效果要差，与文献[3]的结果一致，仔细比对结果可以发现其他两种方法在不同简化率的误差没有确定的大小关系。使用本文方法，得到平整表面和细节表面的简化误差如图5所示。

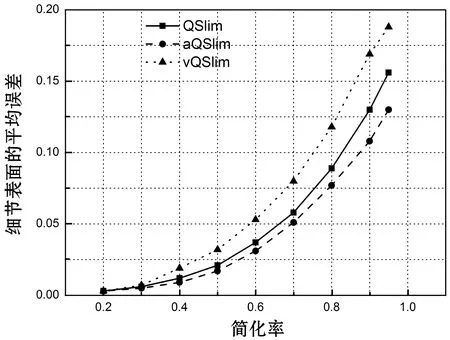
(a)

(b)

(c)

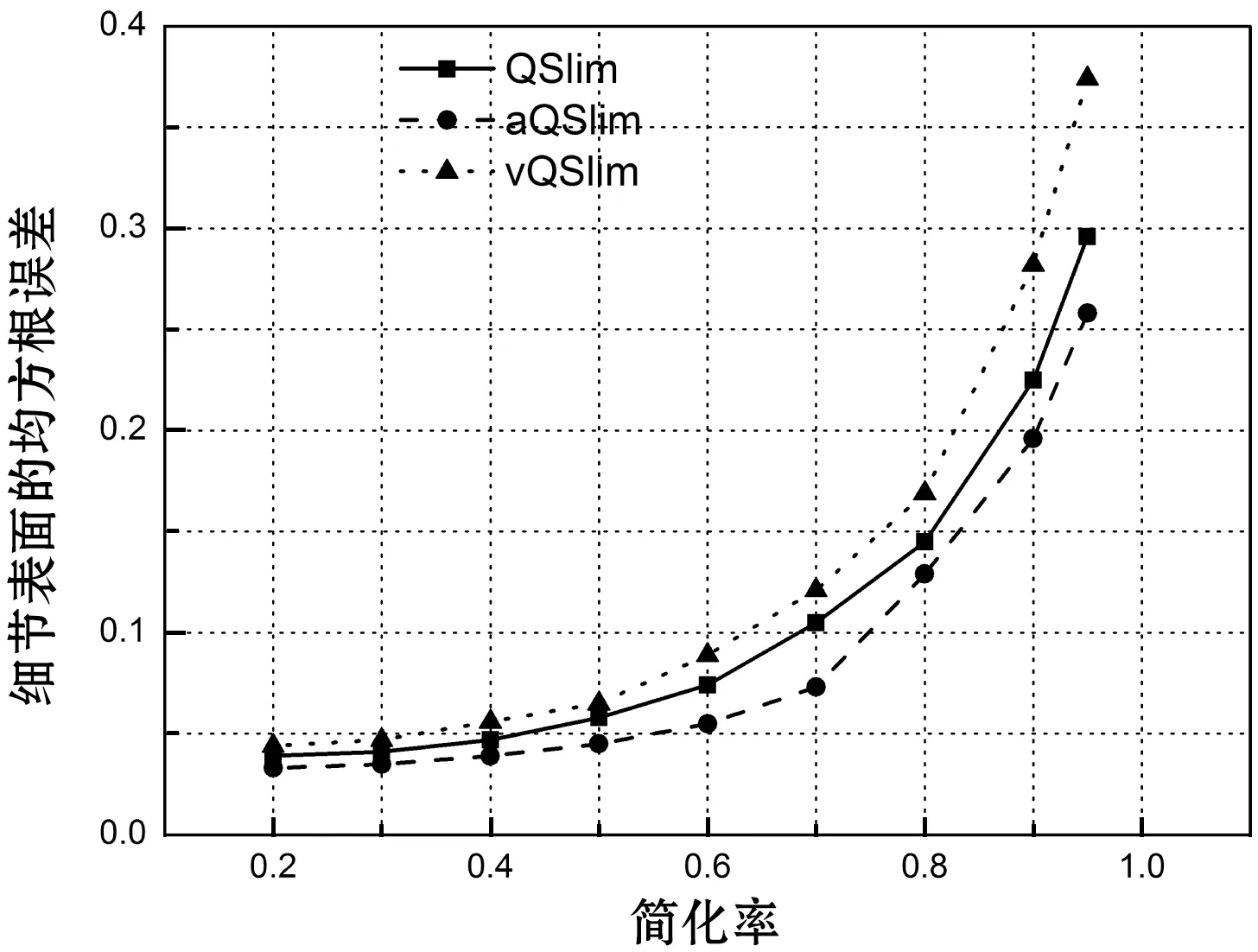
(d)图5 细节表面和平整表面误差

细节表面的误差增长的趋势与整体误差相似，而相对于Metro的结果，已经可以量化三种简化算法的性能。细节表面的简化精度决定UDSM简化后的质量，由图6看出对网格较为复杂的表面的简化效果由高至低aQSlim>QSlim>vQSlim。实验中aQSlim的平整表面网格最少，符合文献[3]的实验结果，在此基础上细节表面的误差说明了aQSlim算法用客观数据表明其对UDSM细节和建筑框架的保持效果。相对aQSlim对平整表面简化精度较差，vQSlim相对于QSlim有微小的优势。通过图5(b)(d)还可以看出分类比较误差方法的均方根误差不稳定性较大，在QSlim和vQSlim的平整表面均方根误差比较中，大小关系不稳定，并且曲线平滑度不理想，不适合算法性能的精确比较，适合异常的监测。

由于UDSM中的平整表面精度不高，而平整表面的简化精度主要指标是其平整度，如图6所示。

图6 平整表面平整度测量结果

平整表面平整度越高，平整度参数ξp越小，基于前文讨论，平整度越高，证明对UDSM平整区域的还原程度越高。图6说明了aQSlim算法对平整区域的还原度较高。而综合图5进行分析，vQSlim简化后对平整网格平整度提升效果最差，而在平整网格误差的降低效果不明显(与QSlim算法相比)。说明以上涉及的评价指标没有绝对的对应关系，都有自身的意义。从理论上说，是aQSlim对平整表面的高简化率导致上述结果，上述实验量化地证明了文献[3]的结论。

图7展示了实验采用的瓦片样貌，和挑选了黑色方框内的网格进行比较。aQSlim明显建筑边缘与地面垂直效果较好，与真实情况相符，从直观效果上说明量化效果是可靠的。还可以看出，简化后的建筑表面更加平整，更符合绝大多数建筑的特征，所以表面平整度参数也可视为评价简化网格质量改善的指标，该平整度参数越低，网格质量改善程度越好。

(a) 实验三角网格表面

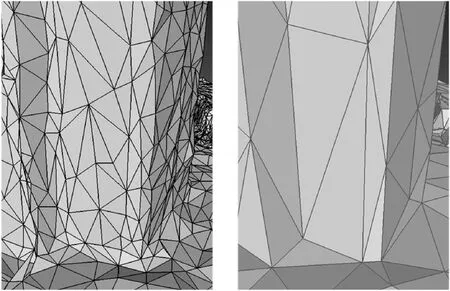
(b)原网格 (c) QSlim简化90%

(d) aQSlim简化90% (e) vQSlim简化90%图7 简化效果直观展示图

表1对整个大连某区域网格，并挑选了该UDSM的三个瓦片，比较本文评估方法与Metro的时间性能。

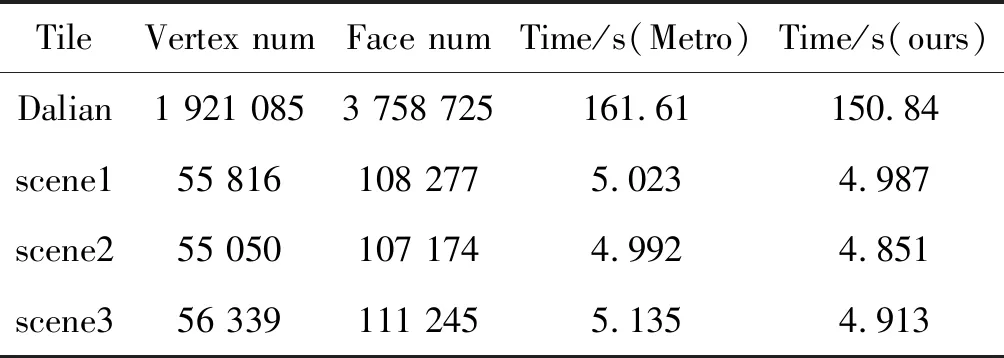
表1 评估方法的时间性能

从时间上看，本文算法比Metro略快。虽然在采样测距前本文要对网格进行分类而且计算参数要多于Metro，然而Metro对简化前后网格需要进行采样并且得到Hausdoff距离。为了保证结果的客观性，比较的时候索引统一采用静态标准网格，即空间栅格索引[3]。

5 结 语

在比较原网格与简化网格误差的研究方面，直到现在，国内外的简化算法改进研究一直使用Metro作为验证手段，本文针对UDSM的网格，改进了长时间未进行改进的网格比较工具。

针对UDSM在非平滑特点，本文对简化网格与原网格的误差评价方法进行了较大改进，将原网格分为平整表面和细节表面两类。针对细节表面的特点，设计出强调建筑物框架误差的基于周长的边扩展采样方法，使得对UDSM细节测量更贴近UDSM的需求，即基于更大程度地保持建筑物的框架结构设计评估方法。针对平整表面倾斜摄影三维重建的建模精度较低，基于对城市地物的认识，引入平整度参数代替与原网格的误差，更加客观地评价平整网格表面。同时简化过程中平整度的提升实际上提升了平整表面的精度，平整度指标从数据上证明了UDSM网格简化并非只是降低城市三维重建的质量。本文提出的评估方法不依赖网格简化算法的任何先验步骤，鲁棒性高。