物联网中大规模无线射频识别标签的容错估计算法
2019-06-17沈平袁瑛周潘
沈 平 袁 瑛 周 潘
1(湖北职业技术学院计算机中心 湖北 孝感 432000)2(湖北职业技术学院信息技术学院 湖北 孝感 432000)3(华中科技大学电子信息与通信学院 湖北 武汉 430074)
0 引 言
RFID技术是物联网领域中极为重要的一部分[1],目前已广泛应用于目标追踪、室内定位、仓储管理等社会生产与人类生活的诸多领域中[2]。在实际的RFID应用中,一个典型的RFID系统主要由后端服务器、RFID阅读器与一系列的电子标签组成。当标签处于阅读器的识别范围内时,阅读器识别标签并通知后端服务器,如果同一个阅读器的识别范围内存在多个标签[3],那么多个标签会竞争同一个信道,导致信号干扰与标签之间的碰撞[4]。目前解决标签之间碰撞问题的方案主要有两种[5]:基于分叉树的确定性算法[6],基于ALOHA的非确定性算法[7]。ALOHA算法的效率较高,该算法根据标签的实际数量动态地调节帧长,从而保持系统效率的最大化,因此,准确估计标签的数量是RFID系统防碰撞重要的预处理步骤[8]。此外,许多应用场景(仓储系统等)也需要统计电子标签的数量,因此,RFID的标签估计是RFID领域一个重要的基础研究课题[9]。
目前主流的电子标签估计算法主要有Low Bond估计算法[5]、碰撞率估计算法[5]与概率估计算法[10]等,其中概率估计算法具有较高的估计准确率,传统的概率估计算法为单阶段估计协议,其计算复杂度较高。文献[11]对传统概率估计算法进行了改进,将估计分为两个阶段,第一阶段粗略地估计,第二阶段再提高估计的准确率,但该算法的时间效率为O(1/2+logN)(其中为置信区间,N为电子标签的数量),对于大规模RFID系统的时间效率较低。
为了解决大规模RFID系统中标签估计时间效率较低的问题,提出一种高效率的大规模RFID标签估计算法。算法在满足期望的准确率前提下,实现了O((1/log2)2)的时间复杂度。现有的标签估计方案利用各个时隙的信息极少(例如:是否为空闲时隙),本文算法则利用较多的时隙信息。此外,被动型RFID标签的计算能力有限,难以生成几何分布的随机数,为此本文设计了一种简单的几何分布随机数生成机制。
1 系统模型
图1所示是移动互联网场景的RFID系统模型,一个普通的RFID系统则包含一个后端服务器、若干RFID阅读器与大量的RFID电子标签。每个阅读器与后端服务器连接,后端服务器控制各个RFID阅读器,初始化标签数量估计的程序,然后,RFID阅读器发送标签估计命令至RFID标签,标签响应阅读器,最终,阅读器将标签响应上报至服务器。

图1 移动RFID系统的网络模型
假设N为RFID标签的数量,N′为估计的标签数量,那么标签估计算法的期望准确率可表示为Pr(|N′-N|≤N)≥1-δ,其中为置信区间,δ为误差率,与δ决定了期望的估计准确率。例如:标签的实际数量为100 000,期望的=0.05,δ=0.01,那么估计结果的区间为[95 000,105 000],最低准确率为99%。
2 标签数量估计
2.1 RFID标签估计的算法
本算法基于Aloha协议[12],但是每帧仅包含一个时隙。图2(a)、图2(b)、图2 (c)分别为服务器、RFID阅读器与RFID标签的算法流程框图。阅读器发出一条标签估计命令,所有的RFID标签同时响应该命令,响应报文的大小相同,每个报文仅有一个比特为“1”,其他比特均为“0”,基于概率为1/(2i)的几何分布选出“1”的比特位。最终共有N/(2i)个标签在各自响应报文的第i比特设置“1”。在协议每轮的标签估计中,服务器搜索所有响应的第一个“0”比特位j,将j作为标签估计算法的输入变量。
根据文献[13],几何hash的结果与数量N之间存在一定的关系,文献[14]设计了LoF机制,将该理论应用于RFID标签估计算法中。本算法基于LoF算法,因为LoF算法在每轮协议中需要多个时隙参与处理,而本算法为了提高计算的效率,仅需要一个时隙,所以需要对LoF算法进行修改。
下文描述了使用几何分布的属性估计标签数量的方法:假设j是响应报文中第一个“0”比特的比特位,j的期望值应当满足下式:
E(j)≈log2(φ×N)
(1)
将式(1)的N与E(j)替换为估计值N′与j,其中φ=0.775 351,N′为标签数量N的估计值,可得下式:
j≈log2(φ×N′)
(2)
根据式(2)可推导出N′:
N′=1/φ×2j=1.289 7×2j
(3)
因为估计的结果是渐近无偏估计,所以本算法通过进行几次独立的估计,将几次估计的平均值作为最终的结果。假设共进行m轮的标签估计,那么最终结果定义为下式:
j′=(j1+j2+…+jm)/m
(4)
式中:j′为平均值,jk为第k轮估计、第一个“0”的比特位。修改后的估计结果变化为下式:
(5)
下文描述了实现期望估计准确率的方法,即Pr(|N′-N|≤N)≥1-δ,其中是置信区间,δ是误差率。假设根据中心极限定理,可得下式:
X=(j′-μ)/σ~N(0,1)
(6)
假设X是均值为0、方差为1的高斯函数,累积分布函数定义为:
(7)
假设一个常量c满足式(8),其中erf是高斯误差函数,通过求解式(8)可获得c:
(8)
Pr[|N′-N|≤N]=Pr[(1-)N≤N′≤(1+)N]=
Pr[log2((1-)φN)]≤j′≤
log2((1+)φN)
(9)
从式(9)可看出,如果-c≥-(log2((1-)φN)-μ)/σ,c≤(log2((1+)φN)-μ)/σ,即可保证Pr(|N′-N|≤N)≥1-δ成立。求解该不等式,可得满足目标估计准确率所需的最小轮数m,如下式所示:
m≥max{[(-σ∞c)/(log2(1-))]2·
[(σ∞c)/(log2(1+))]2}
(10)
综上所述,为了满足给定的标签估计准确率需求,标签估计算法需要运行m轮(每轮需要一个时隙),因此,本算法的时间复杂度为O((1/(log2))2)个时隙。
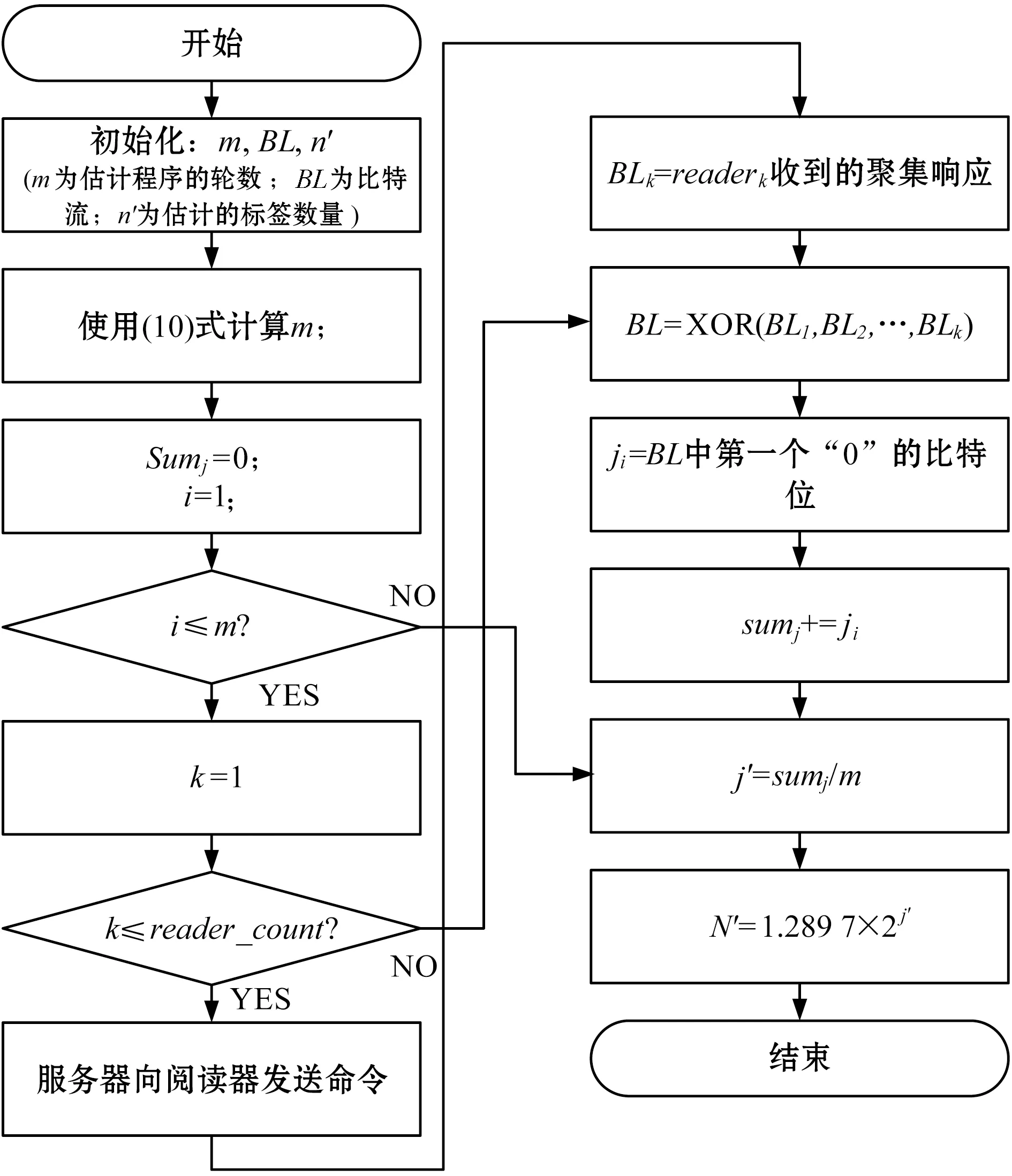
(a) 后端服务器算法
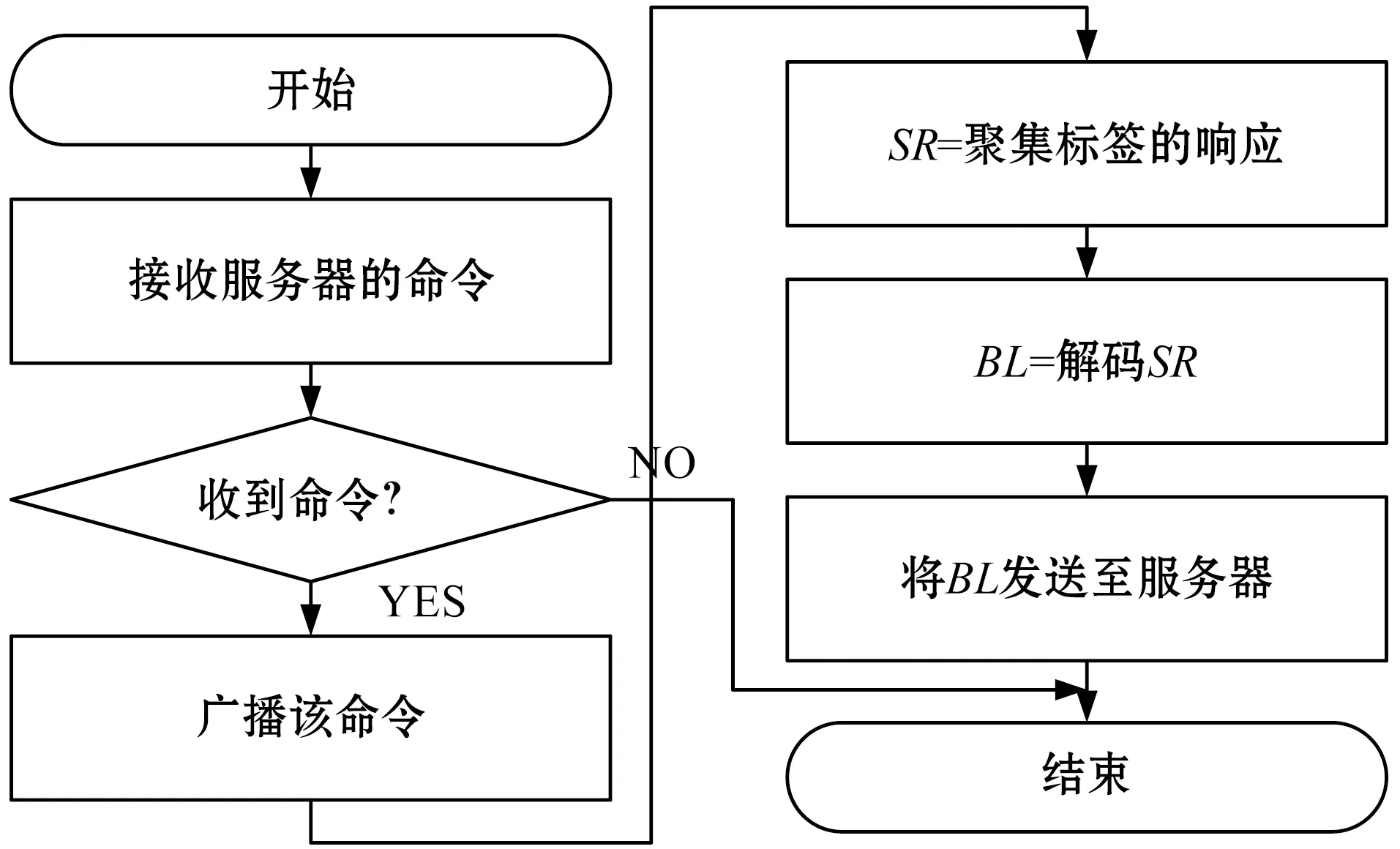
(b) 阅读器的算法
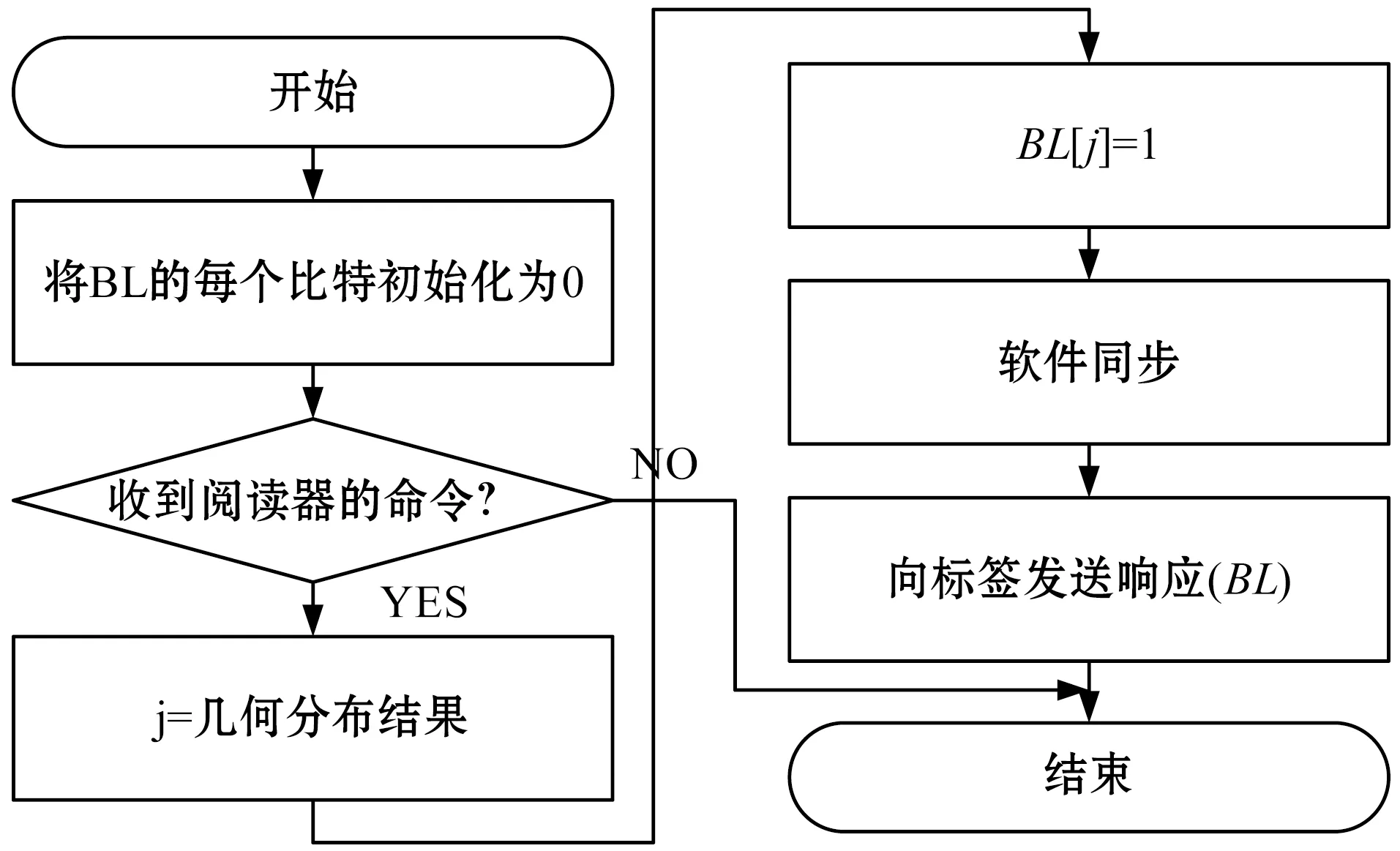
(c) 标签的算法图2 本算法服务器、阅读器与标签的算法
2.2 标签响应的累加
本算法需分析标签响应报文的信息,为此,引入了响应累加的概念,如果多个信号使用相同的频率与相位,那么产生了一个强化的信号,信号的幅度为多个信号之和。在无线网络中,许多研究[15]使用该思想实现数据的洪泛传输。
响应累加需要两个条件:一是多个阅读器同时发送认证报文,另一个是标签响应报文之间的时间偏移应当小于半个脉冲的时长,否则干扰报文之间无法同步。本文的响应累加机制需要多标签的报文为同步传输,在图3中,标签1与标签2的第一个比特为“1”,标签2的第二个比特为“1”。将“1”比特定义为ON信号,阅读器接收同步信号后,获得一个比特序列,其中第三比特是第一个“0”比特,因此,第三比特的信息作为估计的RFID数量。图4所示是标签1、2、3响应比特流累加的信号示意图。标签1与标签2的第1比特位为“ON”信号,标签3的第2比特位为“ON”信号,阅读器的解码结果为“11…”。

图3 EPC C1G2规范的基本处理过程

图4 标签1、2、3响应比特流累加的信号示意图
3 本算法的效率分析
本算法在每轮中仅需要一个时隙,轮数m与期望的估计准确率直接相关,式(10)所需的时隙数量为O((1/(log2))2),优于其他已有的标签估计算法。此外,本算法的时间复杂度主要由误差率决定,与标签数量无关,因此本算法对于大规模的RFID系统具有较高的时间效率。
3.1 标签响应报文的大小
标签响应报文的大小对标签估计的性能具有影响,现有的协议大多采用16比特的响应报文。本协议采用几何分布,因此32比特的报文足以估计232个标签。在开始阶段,标签的数量是未知的,因此本算法将标签响应报文的比特数初始化为32位。在运行阶段,计算各轮j值的平均值,然后将响应报文的比特数调节为j的平均值。例如:RFID系统的标签数量为100 000,那么本算法的响应报文比特数约为16。
3.2 低计算复杂度的几何分布随机数生成机制
本算法需要选择“1”的比特位,该比特位服从几何分布,每轮的估计算法均需要生成该随机数,计算成本较大。本算法的后端服务器生成一个均匀随机分布的随机数,每轮估计程序中,服务器均广播一个新的随机数(表示为Rserver),每个标签中均预置一个独立、随机的随机数(表示为Ri),标签估计程序每轮将Rserver与Ri进行异或操作,生成一个新的随机数,由此既降低了标签生成随机数的计算成本,也生成了满足几何分布需求的随机数。
4 非理想信道的容错机制
大多数文献均假设信道为理想信道,然而,无线信道一般会发生错误。理想信道说明标签响应、阅读器命令与信道检测的成功率均为100%,而非理想信道则说明标签响应、阅读器命令与信道检测的成功率不是100%。跟标签估计过程相关的错误可能有三种情况:(1) 标签响应发生丢包;(2) 噪声或者干扰导致阅读器将一个空闲信道误检为忙信道;(3) 阅读器命令发生丢包。
现有的大多数标签估计算法依赖时隙的模式,因此,它们的估计准确率受信道故障的影响较大。本协议中没有空闲时隙,因为所有的标签均假设在每个时隙中同时地传输响应报文,因此,如果阅读器检测到空闲时隙,则作为第3种错误情况。在第2种错误情况中,干扰与噪声对寻找第一个“0”比特产生影响,如果该轮的j值过大或过小,则忽略该j值。

(11)
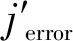
(12)
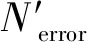
(13)
5 仿真实验与结果分析
仿真实验的标签使用TP-WISP 5.0标签,阅读器则使用USRP N210阅读器,图5(a)所示是USRP N210的实物图,阅读器使用RFX900子版,工作频率为900 MHz,各有两个ALR-8696-C天线。USRP N210通过以太网与一台PC机连接,PC机为Ubuntu Linux操作系统,图5(b)为实验环境图。使用可编程的WISP 5.0硬件与固件仿真电子标签,WISP标签可以无线地吸收能量并具有返回响应的能力,WISP固件则实现了EPC Global C1G2协议[16]。

(a) USRP N210的实物图 (b) 实验环境图图5 实验环境
本文设计的标签响应累加机制需要标签响应时间严格的同步,所以采用三个电子标签来评估标签响应累加机制的效果,图6所示是本协议中阅读器与三个标签之间的通信波形图。在USRP阅读器中增加标签估计命令,阅读器周期地发出标签估计命令,每个标签估计命令包含一个32比特的随机数,每个标签收到标签估计命令后使用收到的随机数生成响应报文,然后将响应报文发送至阅读器。
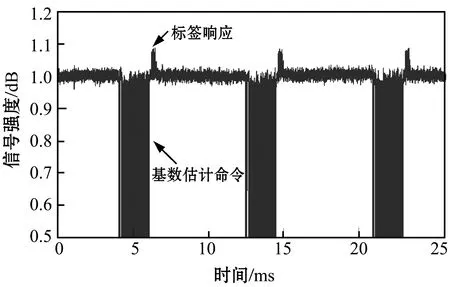
图6 本协议中阅读器与三个标签之间的通信波形
本文设计的标签响应累加机制需要标签响应时间严格的同步。在图7(a)中,阅读器在发送CE命令之后测量了标签响应的时间延迟,响应的时间延迟范围为71 μs~74 μs,响应的延迟偏差主要由标签的计算能力(例如:生成响应的时间)引起。为了使标签响应同步,必须最小化标签响应延迟的偏差,因此在标签响应之前设置一个软件延迟,该软件延迟根据每个标签的计算能力设置不同的时长。图7(b)所示是增加软件延迟之后的波形,可看出99.9%的响应时间均在1 μs的时间段内,所以将响应报文的一比特时长设为2 μs,频率为500 kHz。

(a) 无软件延迟的时序
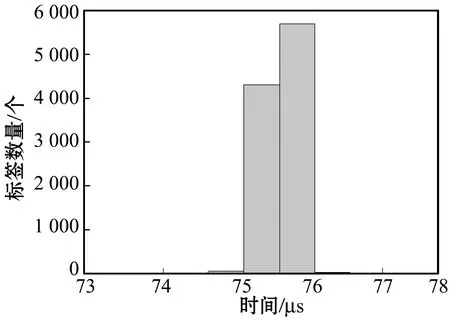
(b) 增加软件延迟的时序图7 阅读器发出命令与收到标签响应的时间延迟
为了评估本文集体干扰的有效性,将三个WISP标签的响应设为不同比特流:标签1与标签2的比特流均为“1000…”,标签3的比特流为“0010…”。图8所示是阅读器接收的信号,图中在0.63 μs~0.65 μs之间的信号幅度最高,该时段两个ON信号叠加,在0.65 μs~0.68 μs之间则无信号,在0.68 μs~0.70 μs之间则有信号,该信号的幅度低于第一比特,来自于第三标签的ON信号。阅读器将接收的信号强度与阈值比较,决定最终聚集的比特流,该案例的比特流为“1010…”。
将3个WISP标签置于阅读器约1米远的位置,进行1 000次重复实验,结果证明99%的结果均符合标签响应累加机制的期望,由此证明了本算法标签响应累加机制的有效性。
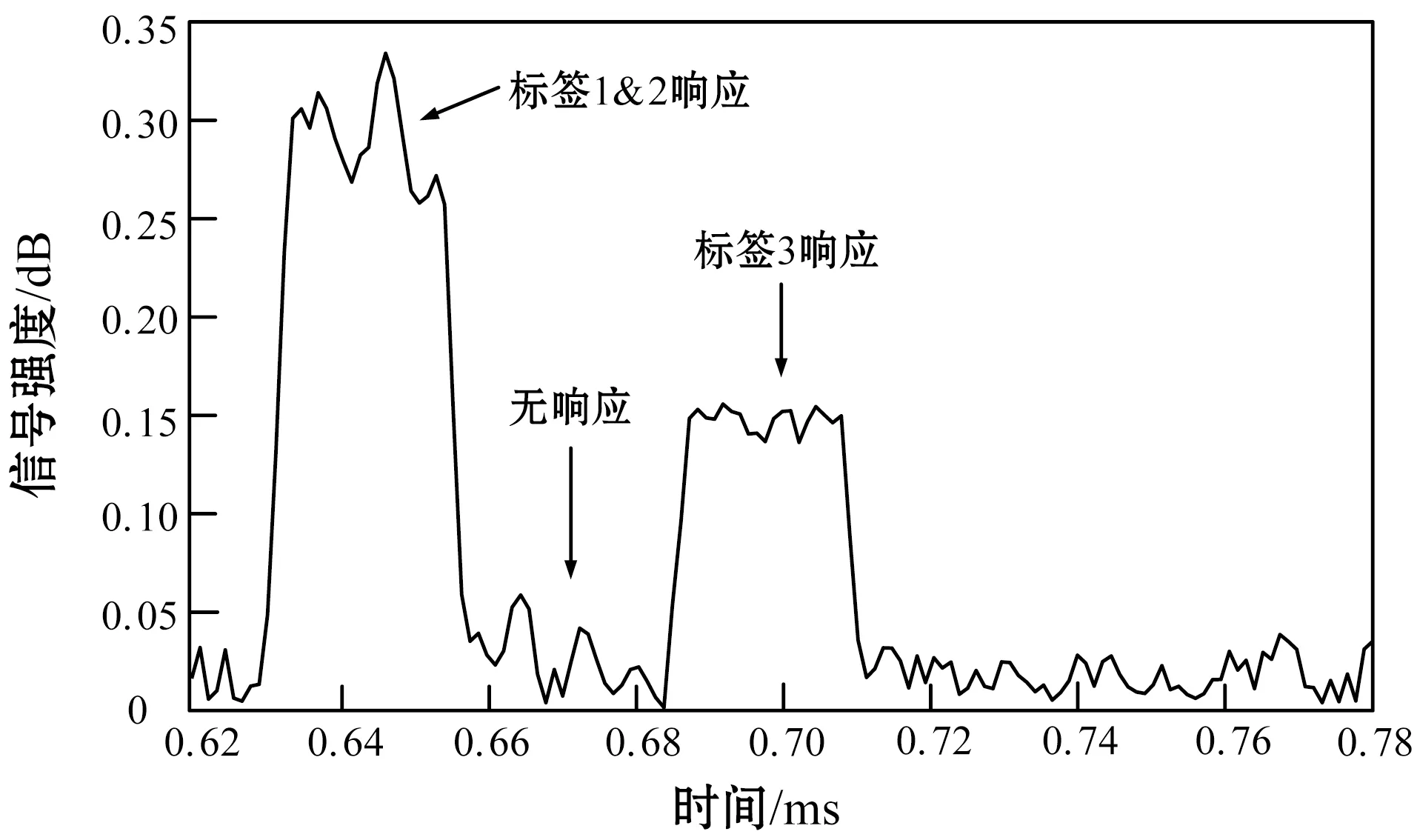
图8 标签响应累加机制实验中阅读器接收的信号
6 对比实验与结果分析
为了评估本算法对大规模RFID系统的标签估计性能,在不同的场景下测试了本算法的性能。基于Python 3.2编程实现了事件驱动仿真平台,表1所示是本文仿真实验的参数。将本算法与AAAS[17]、ZoE[18]与SRC[19]三个大规模标签估计算法进行比较,其中AAAS与SRC两个算法并未考虑非理想信道的场景,而ZOE算法则设计了容错机制,ZOE考虑了第2、3种错误场景,但并未考虑第1种错误场景。

表1 仿真实验的参数设置
6.1 性能度量指标
使用估计误差作为标签估计准确率的度量指标,估计误差=|E(N′/N)-1.0|,式中N′是估计的标签数量,N是实际的标签数量,估计误差越接近0,估计准确率则越高。将各个估计算法使用的时隙数量作为时间效率的度量指标。
6.2 本算法的准确率
图9所示是本算法不同的δ值所获得的标签估计误差,图中δ值固定为0.01,满足估计误差的值变化范围为0.01~0.32。值越低,为了满足期望的估计误差,则估计算法重复的轮数越多。
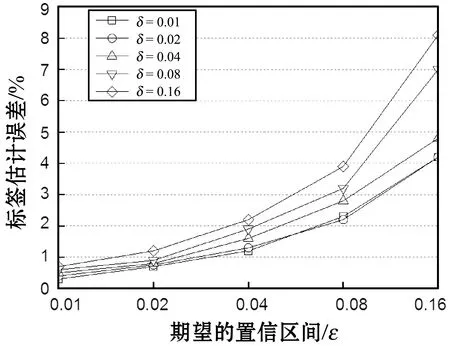
图9 本算法不同的δ值所获得的标签估计误差
6.3 时间效率比较

图10 四种标签估计算法的时间效率结果
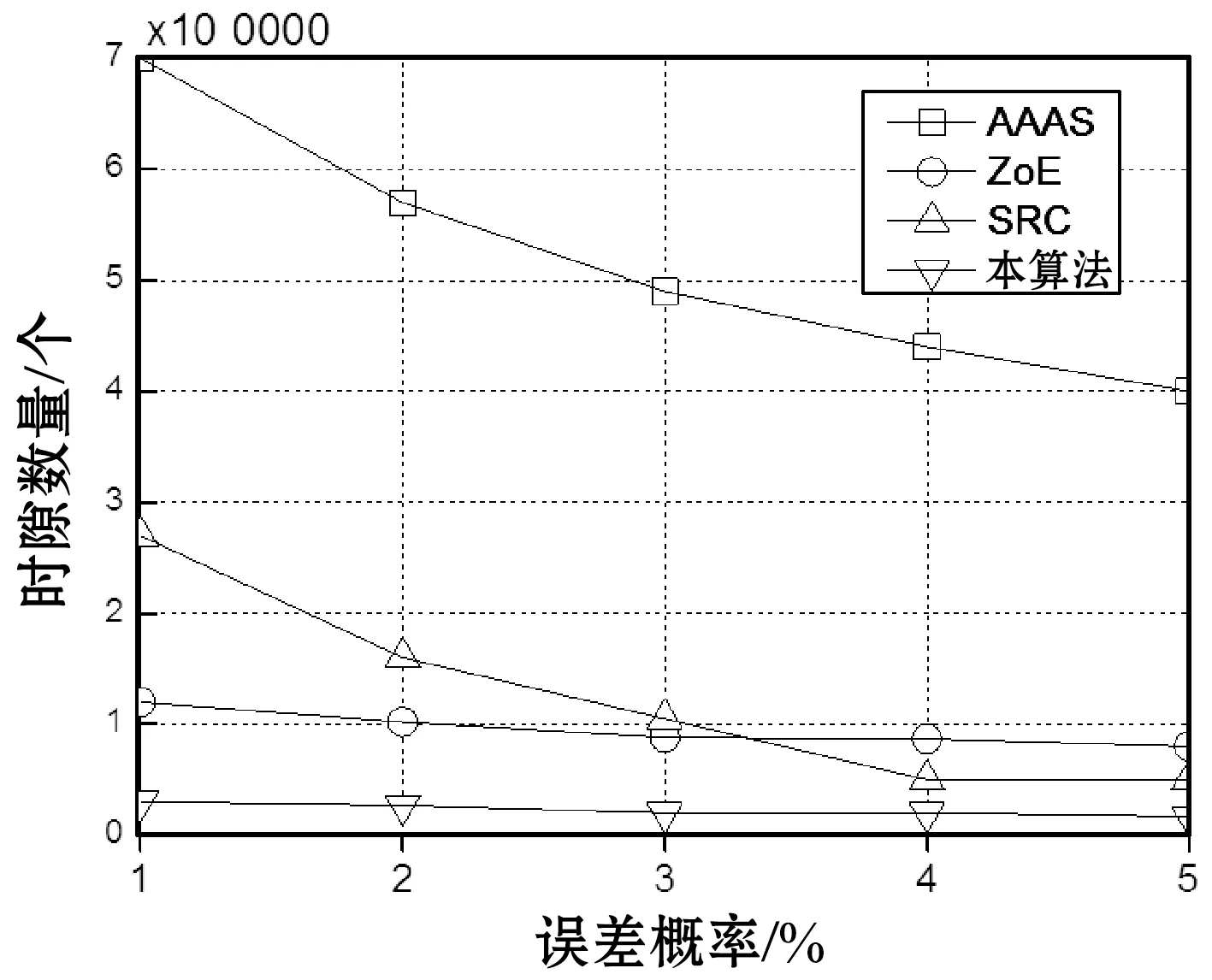
图11 四个算法的时间效率与估计误差之间的关系
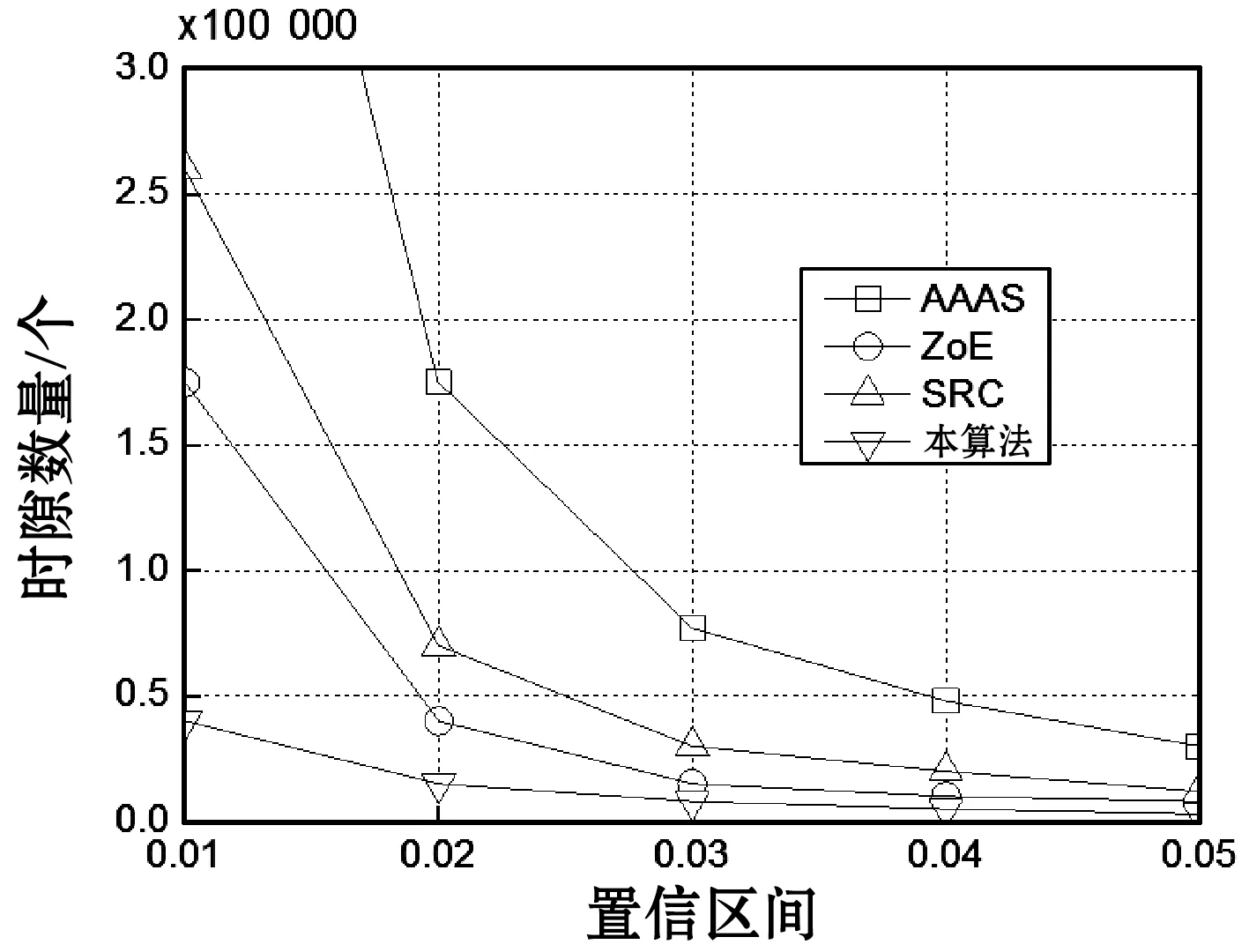
图12 四个算法的时间效率与置信区间之间的关系
6.4 不可靠信道的估计性能
上述实验评估了本算法对于理想信道的估计准确率与时间效率,没有考虑响应丢包、命令丢包与噪声等非理想场景。最终,测试了本算法在不同信道条件下的时间效率与估计准确率。因为上述实验中仅ZOE的性能与本算法最为接近,所以仅将ZOE与本算法进行比较。
图13所示是响应丢包的实验结果,图13(a)表示估计的标签数量与标签响应丢包率的关系,图13(b)表示算法的时间效率与标签响应丢包率的关系。第4节设计了容错机制来解决该问题。图13(a)的标签响应丢包率设为0~32%,可看出随着响应报文丢包率的提高,ZOE算法估计的标签数量逐渐下降,而本算法则基本保持稳定,由此证明了本算法容错机制的有效性,而ZOE算法并未设计这种故障的容错机制。

(a) 估计的标签数量与标签响应丢包率的关系
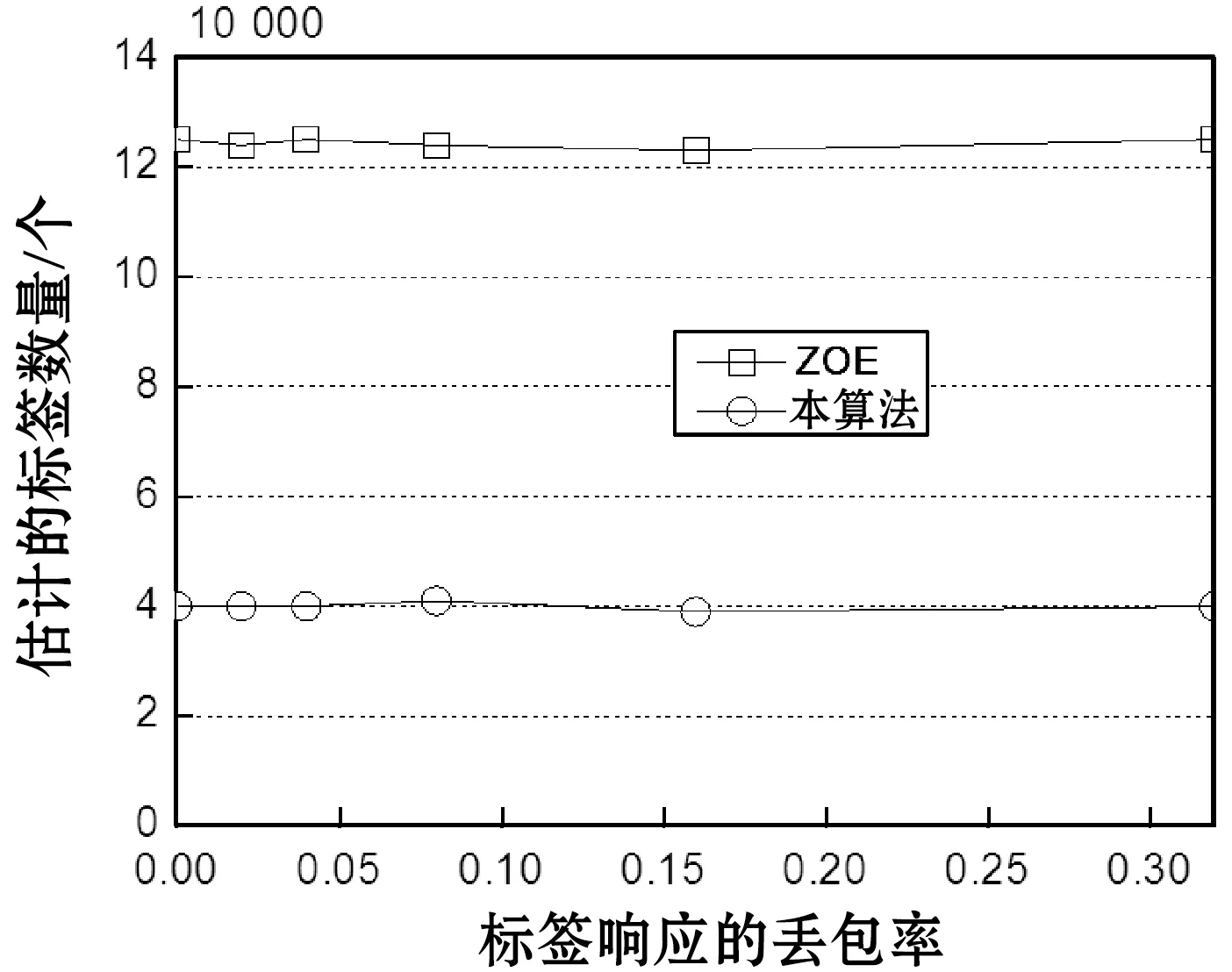
(b) 算法的时间效率与标签响应丢包率的关系图13 标签响应丢包情况的性能
图14所示是命令丢包(噪声或者干扰导致)对标签估计算法性能的影响。本文设计了阈值机制,筛选出合理的j值,如果j值不在预设的阈值范围内,则认为该j值为异常值,并忽略该异常值,仿真实验中将该阈值设为5,假设j的平均值为j′,如果j′-5 (a) 估计的标签数量与信道故障率的关系 (b) 算法的时间效率与信道故障率的关系图14 信道噪声或者干扰情况的性能 本算法不仅提高了标签估计的时间效率,并且实现了容错能力,为了将本算法应用于大规模的被动标签,而被动标签的能量与计算能力均十分有限,所以本算法主要在服务器上进行计算处理,一方面为服务器带来了计算负担,另一方面也增加了服务器与阅读器之间的带宽负担。如果采用分布式服务器与高速的有线网络即可满足本算法的应用需求。 为了解决大规模RFID系统中标签估计时间效率较低的问题,提出一种高效率的大规模RFID标签估计算法,本算法在满足期望的准确率前提下,实现了O((1/log2)2)的时间复杂度。目前基于概率的标签估计算法一般为多时隙、多阶段机制,而本算法则为单时隙、单阶段机制,极大地提高了时间效率,此外,本算法在服务器中生成几何随机数,降低了电子标签的计算负担。本文也考虑了非理想信道的容错机制,对于标签响应发生丢包、噪声或者干扰导致阅读器将一个空闲信道误检为忙信道、阅读器命令发生丢包均取得了明显的效果。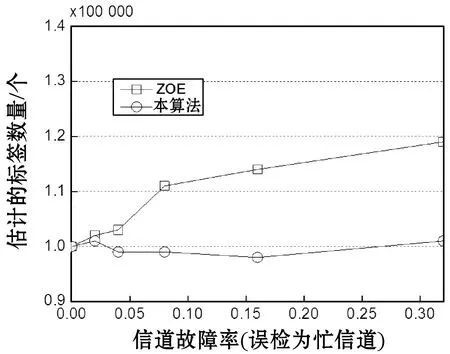

7 结 语
