密码格中行列式的若干定义及性质比较研究

杨 军，李 庆

(西南民族大学计算机科学与技术学院，四川 成都 610041)

量子理论用于密码通信，将引起密码技术的一场变革；受量子计算机攻击，现有的公钥密码体制正面临巨大挑战.美国国家标准与技术研究院(NIST)和国际互联网工程任务组(IETF)[1]目前把“宝”压在制定“后量子时代密码系统的新标准”上，而量子通信则是我国面向2030 年的重大科技项目[2].但是，后量子时代的密码与量子计算的能力极限密切相关，其安全性目前还缺乏足够的理论保证. 近年来，基于格、编码和散列的密码系统、多变元密码学、用误差学习的环及群论密码学等被公认为最有前景的候选方案[3－5].

与量子密码相比具有成本和兼容性优势的“抗量子计算攻击的新型密码”在十余年前密码学界已着手研究.2002 至2018 年，加州大学Micciancio 和麻省理工学院Goldwasser[6]、特拉维夫大学Regev[7]、印度技术研究所Gupta[8]、清华大学王小云[9]、北京大学Wang[10]及武汉大学张焕国等人[11－12]从密码视角较系统地研究了格问题的复杂性、基于格的密码、基于格的认证密钥交换、格密码的数学基础、基于格的小整数解密钥交换问题及抗量子计算密码.

本文研究内容之一是证明比文献[6]中断言“对于满秩整数格Λ ＝L (B)，B 是一个格基，其行列式det (Λ)＝det (B)是整数.”稍强的一个结果.文献[6]及[9，11]分别断言:对于整数格及满秩格Λ ＝L (B)，其行列式det (Λ)是一个格不变量，即不依赖于用于计算它的基B 的选择.主研内容之二是把上述结果推广到任何实数格上.研究内容之三是指出并改进若干文献中几个相关概念的描述小失误案例.

1 格的预备知识

定义1[6]:令ℝm为m 维Euclid 空间.ℝm中的一个格是ℝm中n (≤m)个线性无关向量b1，…，bn的所有整数线性组合构成的集合

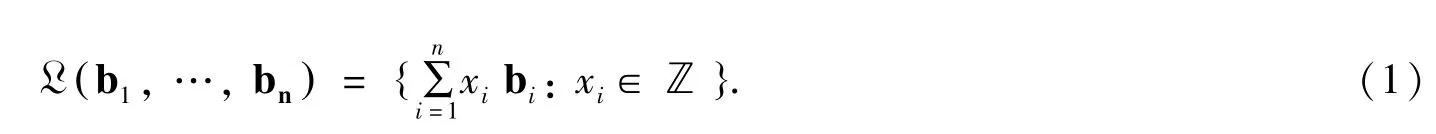
整数n 及m 分别称为此格的秩及维；当m ＝n 时，称其为满秩格.向量组b1，…，bn序列称为一个(格)基，且按惯例把它表示成一个基向量作为列的矩阵(简称基阵)

利用矩阵乘法，(1)式可被改写成另一更紧致的形式

其中，格向量Bx 是通常的矩阵－向量乘法.在全文，格点(即格向量Bx)按惯例均用列向量表示，而AT表示矩阵A 的转置矩阵.

在(3)式中，我们特令B ＝In(n 阶单位矩阵)，可得全整数格.当基阵B∈ℤm×n是整数矩阵，ℤn的子格L B( )称为整数格.

2 格行列式的若干定义及性质的比较

Micciancio 和Goldwasser[6]提出了格行列式的原始定义和一个具体计算公式.

证明:一方面，因Λ 为满秩格，故B 为方阵.再据(4)式及行列式的乘法定理，我们有

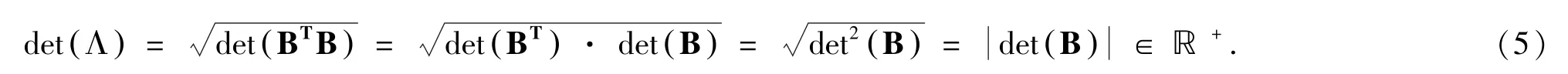
另一方面，又因Λ 为整数格，故B 为整数方阵；再据方阵的行列式定义，知:.另因B 是基阵，故.最后，将以上两个结果代入(5)式，得到

我们证明过程的“一方面”同时也解释了文[7，11]直接给出满秩格的行列式定义的来历和合理性.

注2:值得注意的是，定理1 中的“满秩”虽不是必要条件，但也不是多余条件:若去掉“满秩”，则格行列式不必为整数(甚至不是有理数). 我们构造反例如下. 由整数基阵确定的整数格＝的秩n ＝1 <2 ＝维m，故L ( B)是非满秩的.由(4)式，此时我们有

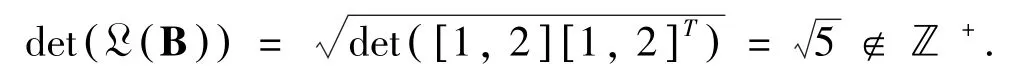
文献[6]及[7，9]分别断言:对于整数格及满秩格Λ ＝，其行列式是一个格不变量.在前人工作的基础上，我们把上述两种情形下的结果统一推广到任何实数格上.

定理2: ℝm中任何一格Λ 的行列式是一个格不变量，即不依赖于用于计算它的基的选择.

证明:令B，B′∈ℝm×n是Λ 的任何两个等价基，即

根据(4)式，需证

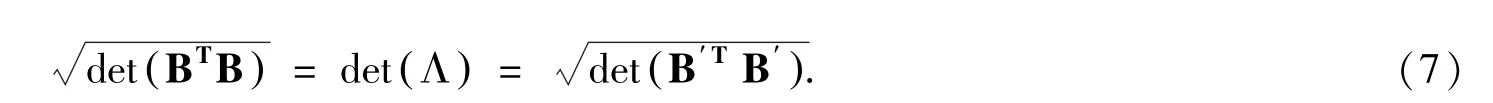
引理1:幺模矩阵U∈ℤn×n(即，行列式＝ ±1 的整数矩阵)的逆阵也是幺模矩阵.

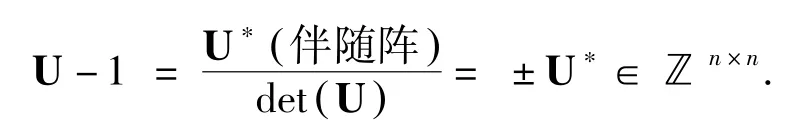
又因

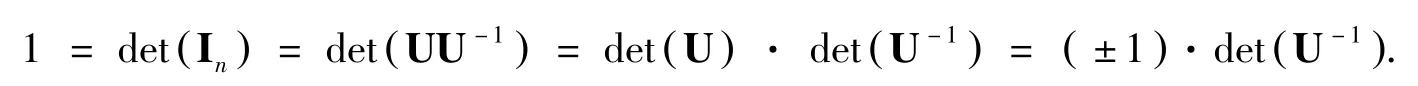
引理2:格Λ 的两个基B，B′∈ℝm×n等价的充要条件是存在一个幺模矩阵U∈ℤn×n，使得B′＝BU.

( ⇒) 设格Λ 的两个基B 与B′是等价的.依基阵的按列分块描述(2)式，令

把(10)式代入(11)式，利用矩阵乘法的结合律，得到

同时，因B 构成ℝ 上的线性空间span (B) ＝{ Bx:x∈ℝn}的一个基，利用同一线性空间的两个基的过渡阵的唯一性[13]，从(12)式我们得到UV ＝In.两端同取行列式，可得

由引理2 的必要性，存在幺模矩阵U∈ℤn×n，使得B′＝BU.于是，

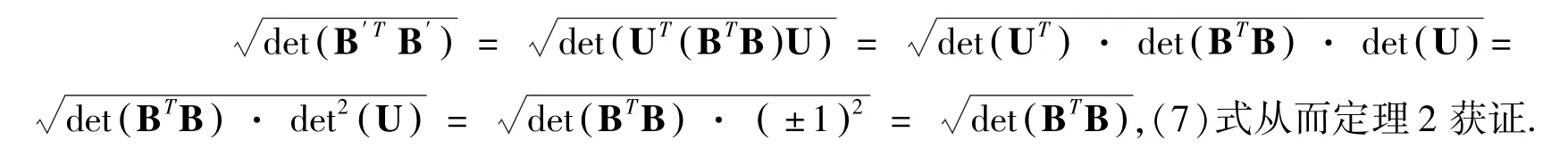
最后，附带指出并改进若干文献中几个相关概念的描述小失误.

注3:文献[6]断言:任何n 个线性无关的格向量的集合B′∈是作为向量空间的的一个基.我们认为，鉴于∈与⊆是一般不能互换的逻辑关系(举一可换特例:若集合A ＝x ∪ x{ }，则x ∈A 且x ⊆A.)，B′∈须改正为B′⊆

注4:文献[8]定义4:由一个基阵B ∈ℝm×n生成的格L 被定义成， 其中Ba 是通常的矩阵－ 向量乘法. 我们认为，集合与矩阵的记号不容混淆，上式与(3)式相比，必须改为＝

注5:文献[11]断言:(满秩格的)行列式的值依赖于基的选择，且与ℝn中格点密度的逆几何相关.翻译应改正为:(满秩格的)行列式的值与基的选择无关，且它在几何上对应于ℝn中格点的密度的逆.

注6:文献[11 －12，14]定义(q 模格):给定正整数q，m，n 及矩阵可以得到一个由A 的行向量生成的q 模格:对应于A 的行向量生成的编码.我们认为，两部分均应改为“由A 的列向量生成”或“由AT的行向量生成”.

注7:文献[10]提出的“基于小整数解问题的格密钥交换协议”关键应用了下面的所谓“结合性”:对于所有(列)向量x ，y ∈ℤm， 恒有等式

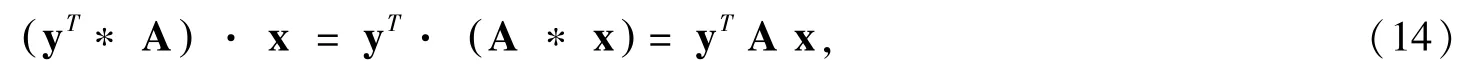
成立，其中∗是在q 模格中用于引入随机扰动向量的一个记号，使得yT∗A 及A ∗x 均是m 维的行向量及列向量； ( yT∗A) · x 是 ( yT∗A)与x 的内积.此性质与经典DH 密钥交换协议中的相似.

剖析如下.尽管(14)式本身从理论上可证，且用仿真软件验证成功，但以上整体描述有三点失误或不妥.第一，根据文献[15 －16]，m 维Euclid 空间ℝm中两个列向量x 与y(标准)内积定义为xTy，记为x · y 或‹x ，y›；两个行向量x 与y(标准)内积类似定义，但行向量与列向量之间无内积定义. 因此，(14)式中的· x 是行向量与列向量x 的矩阵乘法运算结果.

第二，用抽象代数语言讲[17]，命S 是任何一个集合，下列映射

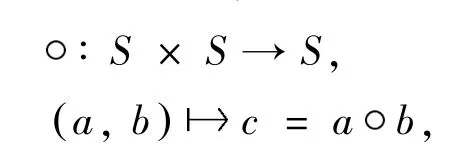
第三，在经典Diffie－Hellman 密钥交换协议中成立，原因是在生成元为g 的循环子群中，非负整数集对于普通乘法运算的交换律演绎出群元素方幂的指数律.结合律与交换律是两个不同的、独立的算律，不能混为一谈.揭示原作者的真正含义:二者的来历不一，但在下文可见它们在密钥交换协议中扮演的作用恰是相似的.

3 结论与展望

本文的工作有三.首先在前人工作的基础上，证明了“满秩整数格的行列式必为正整数”的较强结果(定理1).其次给出了“实数格的行列式是一个与基选择无关的格不变量”的完整证明(定理2).最后指出若干国内外信息安全专业流行教材及文献中看似冲突，实则各有不足之处，并给出具体改进建议.

尽管当前格密码学研究主要应用满秩格，但定理2 不仅本身具有一定的纯粹数学意义，而且对于未来抗量子计算密码学研究提供了一种潜在而更广泛的新视角.事实上，Wang 等人[10]已经率先研究:在秩n≪维m 情形下基于秩亏损的q 模格，首次建立了一类高效实施的密钥交换协议，且已提出抵抗“私钥对攻击”的形式化安全证明.但Mao 等人[14]已对其展开“共享密钥攻击”.对其展开“单方私钥攻击”是本文的未来工作之一.