基于三维交叉阵的相干分布式信号源DOA估计

宋国庆 戴 峥 苏卫民

（1.江苏城市职业学院信息工程学院，徐州，221006；2.南京理工大学电子工程与光电技术学院，南京，210094）

引 言

DOA估计是雷达、声呐和通信系统的重要任务之一。很多高分辨的DOA估计算法被提出，比如最大似然算法[1]、MUSIC算法[2]和ESPRIT算法[3]。在这些DOA估计方法中，信号源被看作是点信号源。然而，由于多径散射效应，信号源发射的信号到达角度可能会在一定的空间范围内发生角度扩展。在这种情况下，将信号源看作是分布式信号源则更加合理。分布式信号源可以分为相干分布式信号源和非相干分布式信号源[4-5]，本文中只考虑相干分布式信号源。

由于相干分布式信号源的未知参数包括：中心方位角、方位角扩展参数、中心俯仰角以及俯仰角扩展参数，DOA估计问题总是需要很高的计算复杂度。近年来，很多低计算复杂度的算法被提出。在文献[6]中，参数估计中的四维搜索被替换成二维搜索，降低了估计器的复杂度，但是不同相干分布式信号源的角信号分布函数必须相同并且已知。在文献[7]中，基于双均匀圆阵，提出了一种连续一维搜索算法估计中心DOA。在文献[8]中，利用均匀圆阵的对称结构，运用广义ESPRIT算法通过二维搜索估计中心DOA。在文献[9]中，基于天线阵列的特殊结构，采用阵列之间互相关算法对相干分布式信号数源的各项参数进行估计。在文献[10]中，利用信号源的一阶近似，提出了一种新的分布式信号源波达估计方法，改善了波达方向估计的性能。然而，在文献[6-10]没有利用信号的特性。在阵列信号处理领域，非圆信号经常被用来改善DOA估计的性能[11-18]。

本文的创新之处在于证明了任意中心对称阵列下的角信号分布权重向量具有对称的结构。基于这一证明，采用三维交叉阵列，运用广义ESPRIT算法，利用子阵间的旋转不变关系估计中心DOA，同时在估计中引入了非圆信号，提高了相干分布式信号源DOA估计的性能，同时算法还具有无需多个相干分布式信号源的角信号分布函数相同或者已知的优势。

1 信号模型

考虑一个三维交叉阵，如图1所示。阵列以坐标原点为中心，由沿着x轴、y轴和z轴的3个均匀线性阵列组成。子阵Xa,Ya和Za分别由Mx,My和Mz个全向阵元组成。所有均匀线阵中的阵元之间的间距为d。假设有D个窄带的、互不相干的相干分布式信号源入射到该阵列上。将三维交叉阵分为两个子阵列，分别为子阵列Za和XYa，那么两个子阵列的阵列接收信号可以分别表示为

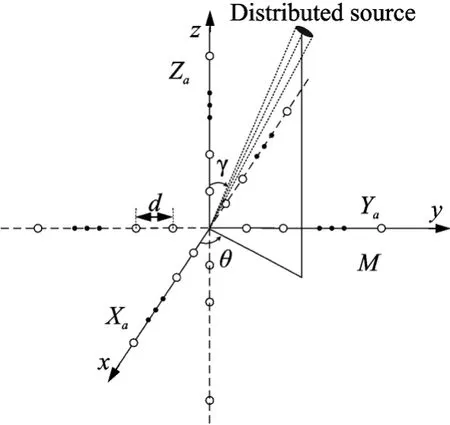
图1 三维交叉阵的阵列结构Fig.1 Configuration of three-axis crossed array

式中：si(θ,γ,t;μi)为第i个分布式信号源的角信号密度函数；向量μi=(θi,σθi,γi,σγi)包含了参数：中心方位角、方位角扩展参数、中心俯仰角、俯仰角扩展参数；nz(t)和nxy(t)是零均值加性高斯白噪声；az(θ,γ)和axy(θ,γ)分别为角度(θ,γ)处的两个阵列流形向量

式中：ax(θ,γ)，ay(θ,γ)和az(θ,γ)分别为沿x轴、y轴和z轴的子阵列的阵列流形向量，可以表示为

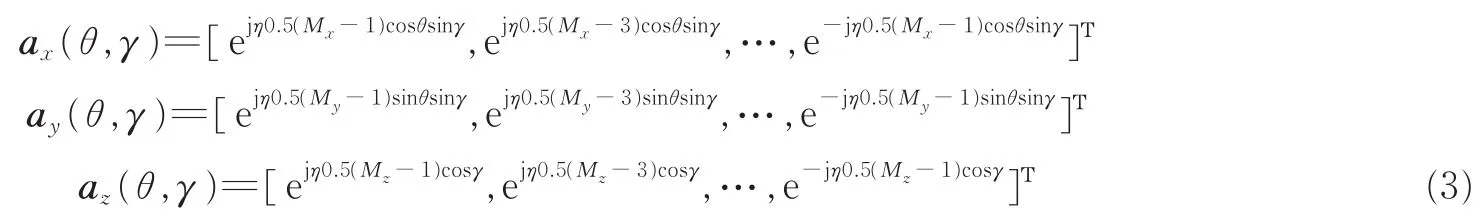
式中：η=2πd/λ，λ为载波波长。

对于相干分布式信号源的二维DOA估计问题，角信号密度函数si(θ,γ,t;μi)可以写为

式中：si(t)为相干分布式信号源的生成信号，ρi(θ,γ;μi)为角信号分布函数。此时相干分布式信号源的广义阵列流形向量可以表示为

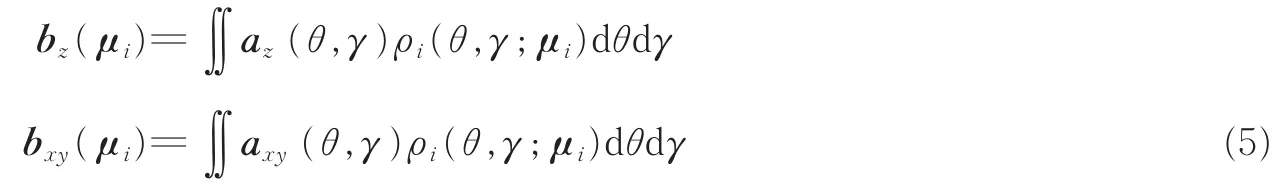
在小角度扩展下，式(5)可以写为

式中：⊗表示Hadamard乘积，gz(μi)和gxy(μi)分别为角信号分布权重向量。那么，式(1)中的观测向量可以写为

式中：s(t)=[s1(t),s2(t),…,sD(t)]Τ为D×1维的信号向量；Bz(μ)和Bxy(μ)为广义阵列流形矩阵。

在本文中，考虑具有最大非圆率的非圆信号，那么信号向量s(t)可以表示为[13-14]

式中：s0(t)=[s01(t),s02(t),…,s0D(t)]由实信号组成；Φ1/2是包含每个信号的非圆相位φi的对角矩阵，即有

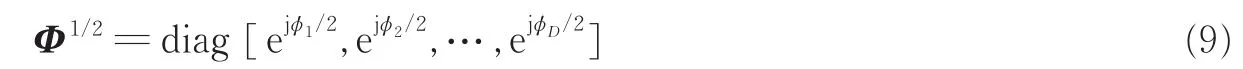
当非圆信号入射到阵列上时，为了充分利用信号的非圆特性，阵列观测向量及其共轭将合并来扩展阵列的输出信号，扩展后的阵列输出信号可以分别表示为

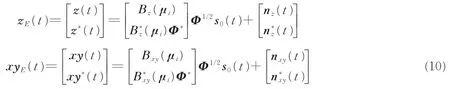
2 算法描述

本节将分3步描述所提算法：（1）证明中心对称阵列的相干分布式信号源的角信号分布权重向量具有对称结构；（2）描述中心俯仰角的估计过程；（3）描述中心方位角的估计过程。

首先证明在中心对称阵列中，相干分布式信号源的角信号分布权重向量具有对称结构。考虑以坐标原点为中心，由M个相同的天线单位组成的中心对称阵列，第m个阵元的位置为(xm,ym,zm)。因此，理想情况下点信号源的阵列流形向量可以表示为

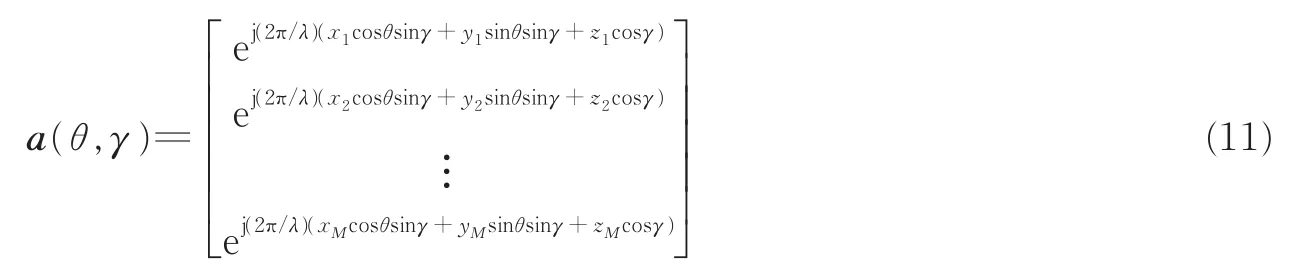
对于小角度扩展，基于泰勒级数展开[19]，b(μi)中的第m个元素可以写为

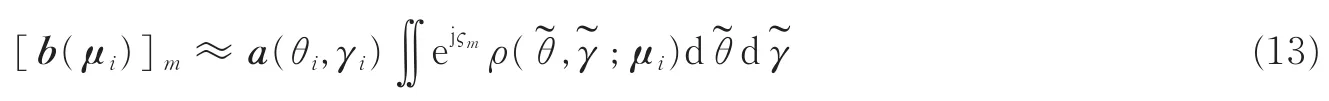
因此，角信号分布权重向量可以写为

对于中心对称阵列，有 (xm,ym,zm)=-(xm+M/2,ym+M/2,zm+M/2)，因此ςm=-ςm+M/2。 由于是单峰对称函数，即有

由于子阵列Za和XYa是中心对称阵列，因而

由式(15)可以证明：对于中心对称阵列，相干分布式信号源的角信号分布权重向量具有对称的结构。

2.1 中心俯仰角估计

在子阵Za中，广义阵列流形向量扩展为

定义2Mz×2Mz维的选择矩阵H为

式中：ΠMz是Mz×Mz维的置换矩阵，0Mz为全零矩阵。基于式(16)中gz(u)的对称特性，存在如下的旋转不变关系

式中

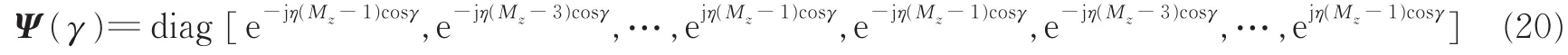
定义复变量k=ejηcosγ，那么Ψ(γ)可以写为

假设Us是信号子空间矩阵，对应了的D个最大的特征值。当Rs=E{s(t)sΗ(t)}满秩时，Us的列张成的空间和向量V=[v(μ1,φ1),…,vD(μD,φD)]张成的空间是同一空间。此时，存在一个唯一的D×D维的非奇异矩阵，使得Us=VT。根据广义ESPRIT算法[20]，引入矩阵Fz(k)，有

因此，当Ψ(ki)=Ψ(k)时，Fz(k)的第i列是零向量。通过求解k的值可以估计出中心俯仰角，即有

中心俯仰角的估计值可以表示为

值得注意的是，只需要得到k的D个值，但是该方程可以求解得到超过2D个值。使用单位圆内的根，并选择最靠近单位圆的D个根作为DOA估计对应的根。

2.2 中心方位角估计

在子阵XYa中，广义阵列流形向量可以扩展为

定义4Mz×4Mz维的选择矩阵为

基于式(16)中gxy(μi)的对称特性，有如下的旋转不变关系

式中

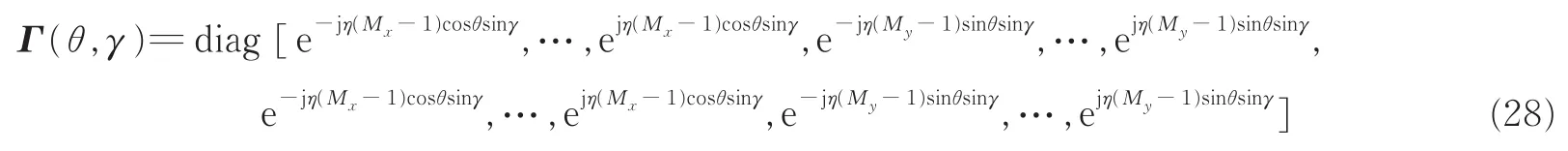
相似地，定义U′s为信号子空间矩阵，那么存在唯一的D×D维的非奇异矩阵T′使得U′s=WT′。根据广义ESPRIT算法[15]，引入矩阵Fxy(θ,γ)，有

因此，当Γ(θi,γi)=Γ(θ,γ)时，矩阵Fxy(θ,γ)的第i列是一个零向量。利用先前的中心俯仰角估计值，可以通过搜索如下的谱函数估计中心方位角，有

值得注意的是，每一个已经估计出的中心俯仰角都对应这样一个方程。

3 仿真实验

本节将所提算法与连续一维搜索（Successive one-dimensional search,SOS）算法[7]的计算复杂度进行比较。假设阵列阵元数为M，接收信号的快拍数为L，相干分布式信号源的个数为D，每一维的谱搜索点数为N。此时，所提算法的运算量体现在矩阵运算和空间谱搜索上，其计算复杂度可以表示为

SOS算法的计算复杂度为

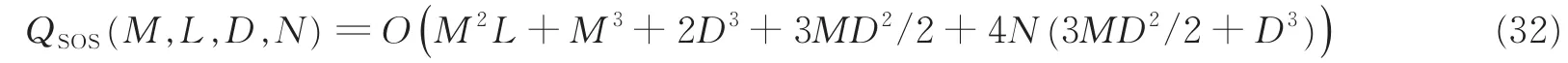
当谱搜索点数N比阵列阵元数M和信号源个数D大得多时，有

因此，所提算法的复杂度要略低于SOS算法。

在以下每个实验中，噪声是零均值高斯白噪声，仿真所用的非圆信号是BPSK信号，非圆率是随机的。快拍数为200，搜索步进为0.01°。三维交叉阵列一共由36个全向阵元组成，每一个子阵有12个阵元。相邻阵元之间的间距为0.5λ。两个相干分布式信号源的参数为μ1=(30°,3°,20°,5°)和μ2=(60°,4°,70°,4°)。在实验中，均方根误差定义为。仿真参数如表1所示。

表1 仿真参数Tab.1 Simulation parameter

在第1个实验中，验证所提算法是否不依赖于角分布函数。仿真了3种情形，两个相干分布式信号源的角信号分布函数都是均匀分布、都是高斯分布以及一个是高斯分布、一个是均匀分布的情况。在500次Monte-Carlo实验后，中心DOA估计值的RMSE随信噪比的变化曲线如图2所示，从图中可以看出，所有情况均有良好的估计性能。

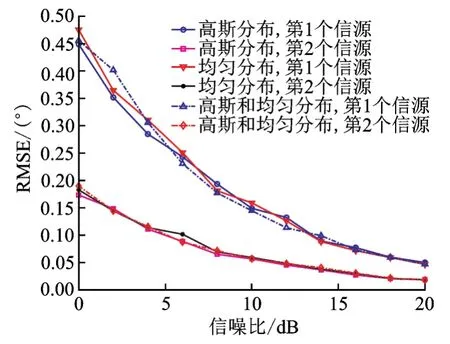
图2 中心DOA估计值的RMSE随SNR的变化曲线Fig.2 RMSE curves of central DOA estimates with SNR

在第2个实验中，选择SOS算法[7]与所提算法进行比较。SOS算法作为经典的相干分布式信号源二维中心DOA估计算法，首先利用两个子阵间的旋转不变关系估计出分布式信号源的中心俯仰角，然后利用广义阵列流形向量的结构特性，针对估计出的不同中心俯仰角，通过连续的一维搜索估计出对应的中心方位角。相比于大部分的二维谱搜索算法[6,8]，SOS算法在具有更低计算复杂度的同时，保证了算法的估计精度。

对于SOS算法，需要利用双均匀圆阵。为了进行合理的比较，双均匀圆阵共由36个阵元组成，每一个圆阵具有18个阵元，阵列结构如图3所示。两个阵列之间的垂直间距为0.5λ，圆阵的半径为λ/(4sin(π/18))，因此子阵内阵元间的间距为0.5λ。在500次Monte-Carlo实验后，中心DOA估计值的RMSE随信噪比的变化曲线如图4所示，可以看出所提算法的估计精度相比SOS算法有更大的优势。双均匀圆阵和三维交叉阵都属于三维空间阵列，本文中基于三维空间阵列的算法在计算复杂度和估计精度上都比文献[7]中的SOS算法略有优势，为相干分布式信号源的中心DOA估计提供了更多的的阵列选择。非圆信号引入，使得算法可以同时利用E{ss∗}和E{s2}，提高了信息的利用率，因此性能得到了提升。

从图4中可以看出信号源2的估计误差要小于信号源1，估计误差通常会与克拉美-罗界进行比较，因此产生这种现象的原因类似于计算不同信号源角度估计的克拉美-罗界，估计误差和克拉美-罗界随信噪比的变化曲线都与信号源的实际方位有关。

4 结束语

图3 双均匀圆阵的阵列结构Fig.3 Configuration of double uniform circular arrays

图4 相干分布式信号源的中心DOA估计性能比较Fig.4 Central DOA estimation performance comparison of CD source

本文借助非圆信号，提出了一种新的方法来估计相干分布式信号源的中心DOA。算法采用了一个三维交叉阵列，将该阵列分为两个子阵列。当引入非圆信号后，阵列接收信号被扩展。基于广义ESPRIT算法，本文利用求根的方法估计出中心俯仰角，然后通过多次一维搜索估计中心方位角。所提算法的显著优势是非圆信号带来的估计精度优势。此外，所提算法可以应用于相干分布式信号源具有不同角信号分布函数的情况。