基于稳健估计的混凝土抗压强度测试分析

张 博，贾 敏，吴 兵，张恒嘉

(华北理工大学 矿业工程学院，河北 唐山 063210)

强度是评价水泥混凝土质量的重要指标，在硬化过程中混凝土强度是逐渐增长的。许多学者通过各种试验对混凝土的抗压强度进行了测试和研究，其中王玲玲等人利用正交试验研究了原材料成分、配合比等对绿化混凝土不同养护期内的强度、透水系数等性能的影响[1]；刘亚力等人通过混凝土28 d强度试验对测量不确定度进行分析，得出了测量不确定度的数学模型[2]；另外刘海峰对单掺粉煤灰、单掺沙漠砂、双掺粉煤灰和沙漠砂混凝土3 d，7 d，14 d和28 d抗碳化性能进行试验，得出了混凝土28 d碳化深度与沙漠砂替代率之间的回归关系模型[3]。这些试验大多采用最小二乘法对离散的混凝土压强数据进行建模分析，用以考察混凝土的一些力学性能，但是，在测试过程中由于存在操作人员情绪波动、素质差别、技术能力等人为因素以及各种计量器具的精度误差等，会引起混凝土强度的测量偏差[4]，从而对所建模型造成干扰，因此，本试验选择稳健估计对28 d养护期内混凝土的抗压强度值变化进行曲线拟合，并对比最小二乘法，以检验稳健估计在该模型中的可靠性。

1 基础理论

将成型的混凝土试块浸泡于水中，并置于恒温恒湿箱进行养护。随着时间的延长，混凝土由可塑体逐渐转变为坚固的石状体，在这期间混凝土的抗压强度会随着养护时间的增长而增强，前期增长较快，中期增速放缓，到后期压强趋于稳定。根据这一特点采用三次多项式[5]对混凝土抗压强度与时间的数据来进行曲线拟合。

三次多项式曲线拟合模型为：

y=a+bx+cx2+dx3。

(1)

式中，a，b，c，d为模型待定参数，x为自变量(d)，y为因变量压强值(MPa)。根据(1)式可列出误差方程：

δ=βx-y。

(2)

式中，δ为压强值改正数，β为系数，y为实测压强值。各参数可写成如下矩阵的形式：

(3)

(4)

在混凝土测试过程中，实验人员计量、实验不规范等操作会不可避免引入误差，从而导致混凝土的抗压强度测量结果存在误差。因此本文选用稳健估计准则对参数进行估值，并与传统最小二乘法进行比较。

(5)

式中σi，pi，wi分别为第i点对应的抗压强度值的误差、稳健权因子和等价权。

为了降低试验中误差的影响，抗压数据采集时每次测试3块混凝土试块，取平均值作为最终的数据，设总体X～N(μ，σ2)，即正态总体下μ的置信度为1-α的置信区间为：

(6)

其中，α为置信水平，s是标准差，n是自由度。

2 原材料及配合比

本试验中，水泥采用的是“冀东牌”P.O.42.5普通硅酸盐水泥，其性能指标见表1。

表1 水泥的主要性能指标

砂为“艾思欧牌”ISO标准砂，水选取普通自来水，每组胶砂的质量配合水灰比为0.5，每组材料需要量如表2所示。

表2 材料需要量

胶砂试件一组由3条规格为40 mm×40 mm×160 mm的棱柱体组成，共设计30组混凝土试件，28组为试验组，2组为备用组，备用组用来补足试验过程中试验试件不合格的试验组。

混凝土试件的制作，按《混凝土强度检验方法(ISO法)》GB/T17671-1999中的试验规范制作试验试块，用标准称称取原材料，1 d后进行拆模，将30组试件同时放入水泥标准养护箱进行标准养护。

3 试验

3.1 试验数据

按上述试验方案测得混凝土试块在不同龄期、相同养护条件下的抗压强度值，试验数据见表3。

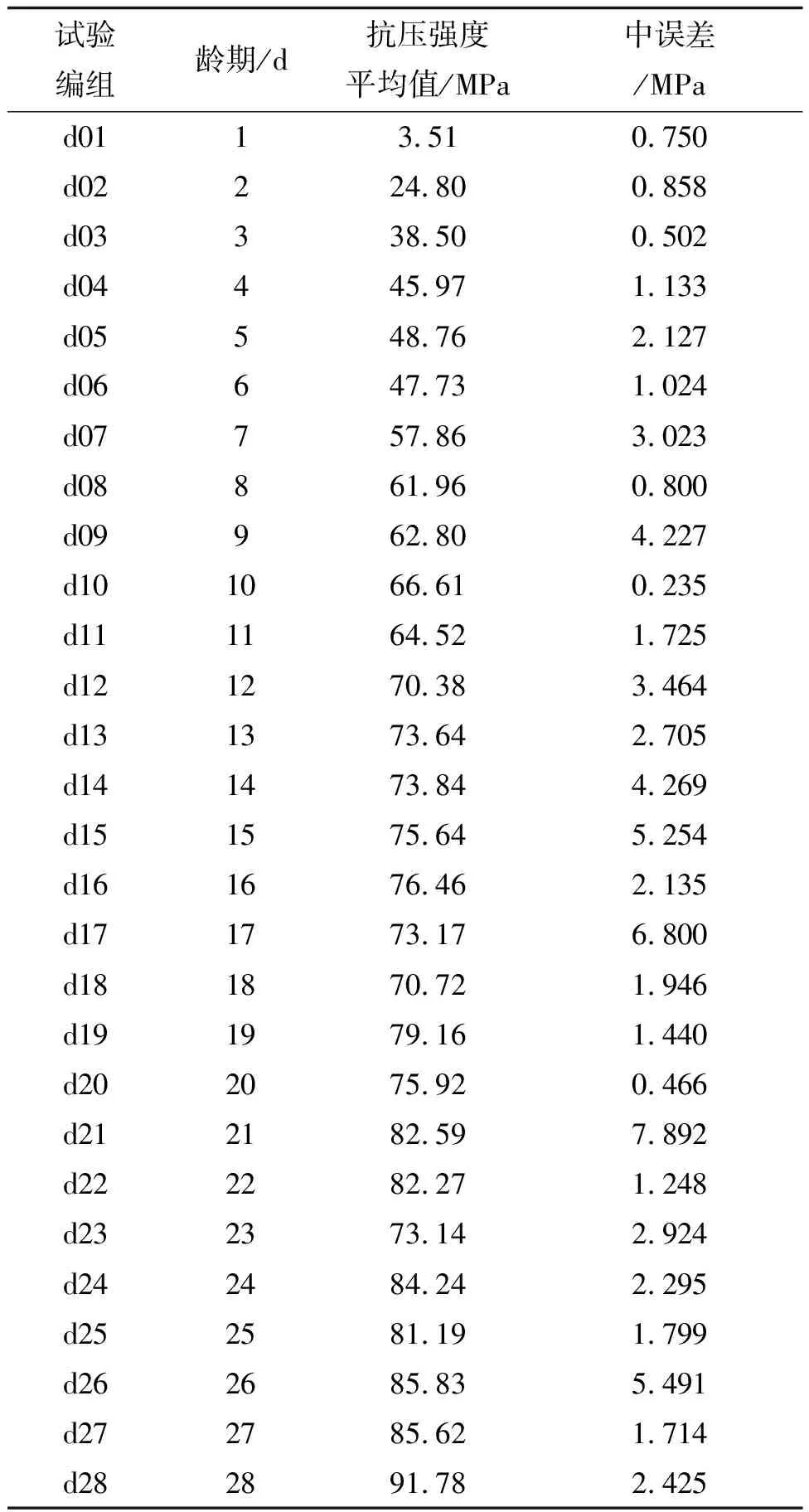
表3 试验数据

根据式(6)代入相关参数，计算可得置信度是95%的置信区间为：

由置信区间可得如表4所示的存在较大误差的数据。试验过程中无法避免会引入误差，此时最小二乘不能拟合得到最佳的模型参数。

根据表3中部分试验数据绘制平均抗压强度值的散点图，如图1所示。

从图1中可以看出，抗压强度值随养护时间的增长呈现递增的趋势，前8 d增长较快，压强值高速增长；8-18 d增速稍缓；18-27 d抗压强度值增长缓慢，近乎趋于稳定。

表4 较大误差数据

图1 抗压强度均值

3.2 数据拟合

由于三次多项式函数图像既符合如图1所示的递增性，又能保证一定的精度，因此选择三次多项式函数来进行对图1数据的曲线拟合。

依据本文“基础理论”部分的公式和理论，利用Matlab软件对表3中(龄期为1-24 d的数据)分别进行普通最小二乘法和基于选权迭代的稳健估计法的三次多项式拟合，拟合结果如图2所示。

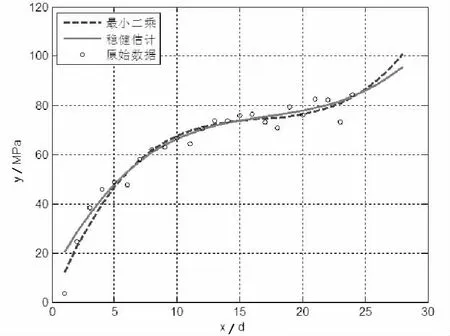
图2 拟合曲线

曲线的最小二乘表达式：

Y1=0.0148x3-0.7389x2+12.6600x+0.0659。

(7)

曲线的稳健估计表达式：

Y2=0.0010x3-0.5192x2+9.7270x+11.0400。

(8)

最小二乘：

RMSE=4.26。

稳健估计：

RMSE=3.88。

RMSE值越小表示精度越高，由此可见，稳健估计的精度优于最小二乘。

3.3 验证

为了对比稳健估计和最小二乘法分别在该模型下的可靠性，根据(7)式和(8)式分别计算出龄期为25-28 d的预测结果，如表5所示：

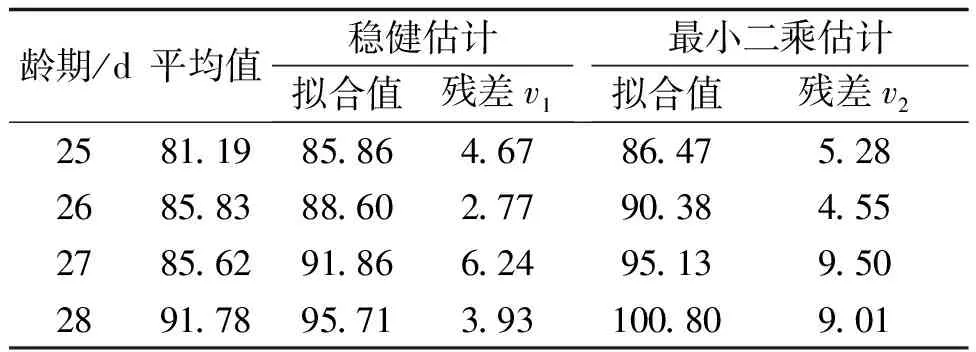
表5 拟合数据

将表5中数据v1和v2分别进行归一化之后计算其残差平方和(V=vTv)得：

最小二乘：V1=1.833；

稳健估计：V2=1.407。

由V2

4 结论

在对混凝土进行抗压强度测试的过程中，往往会不可避免地引入粗差。本文通过稳健估计与最小二乘法对存在较大误差的混凝土压强试验数据进行对比处理，体现了稳健估计的优越性。稳健估计在采用的假定模型下，所得参数的估值对模型的表达更为理想，不会导致参数的估值产生较大的偏差，很大程度上避免了粗差给试验带来的不良影响，保持了较高的拟合精度，从而得到与实际更接近的拟合效果；而且即使是在数据欠缺的情况下，运用稳健估计也可以进行较为准确的预测，保证试验结论的准确和可靠。因此，本试验证明，运用稳健估计相较传统最小二乘对混凝土抗压强度的预测结果更加接近最优。