泵控马达系统恒转速控制器设计与FPGA实现*

成 钊，王和明，张 勇，张 颖

（空军工程大学防空反导学院，西安 710051）

0 引言

随着现代科技的进步和现代战争模式向信息化发展，军用装备的小型化，模块化以及集成化是研究的热点方向。现代军用车辆的车载设备需要大功率、高稳定性和可持续性电力系统的支持，因此，其工作的传统方法多采用驻车部署模式；而在车载设备机动供电方面多采用蓄电池供电模式，具有笨重、不可靠和不可持续的缺点，这两种模式均严重影响了军队的战斗力。基于这一现状，行车取力发电成为解决这一问题的较优解决方案。

国外行车取力发电技术已经开始应用于工业领域和军事领域，美国、德国的行车取力发电技术实现了产业化［1-2］。芬兰Dynaset公司在行车取力发电液压调速系统的研究上，已经有了一些成熟的产品［3］。在我国，行车取力发电也成为热点研究问题。北京理工大学的郭初生利用带补偿的PI控制器对输入转速处于时变情况下的泵控马达系统进行了系统建模与仿真［4］，证明了带补偿的PI控制器能够有效克服转速波动对泵流量的影响。北京交通大学的聂磊对行车取力发电系统恒速控制策略进行了深入研究［5］，车辆发动机转速在600 r/m～2 400 r/m变化时，交流用电功率在0 kW～16 kW变化时，系统超调量小于6.6%，稳态误差小于0.1%。北京交通大学的张吉军［6］利用常规PID控制器对泵控马达系统进行了实验验证，结果表明系统性能比较稳定，但由于负载突变转速也会改变，系统超调量会不断变化。北京理工大学的李晓林针对变量泵转速时变和负载扭矩突变的特点，利用动态面控制、LQ最优控制等现代控制方法设计控制器［7-8］，仿真结果表明所设计的控制器可以满足泵控马达系统的技术要求。

立足于目前的研究情况，国内学者设计的泵控马达系统调速器稳态输出转速波动较小，稳态性能都比较好。但是在如何提高系统的快速响应能力，减少超调量，以及在负载突变情况下提高系统的稳定性等方面依然需要深入研究。为提高泵控马达系统快速响应能力和增强其在负载突变情况下的稳定性，本文根据机理性建模方法建立了变量泵恒流量数学模型，设计了一种参数基于偏差和偏差变化率的指数函数的非线性PID控制器。利用FPGA完成非线性PID控制器的硬件实现，基于“FPGA+SOPC架构”设计了泵控马达恒转速输出控制系统。实验验证了本文设计的控制器对系统恒转速输出控制具有较好的可行性。

1 变量泵恒流量数学模型建立

在变量泵流量调节过程中，起主要调节作用的元件为比例电磁减压阀、伺服阀、斜盘和轴向活塞［9］。变量泵的工作原理如图1所示。

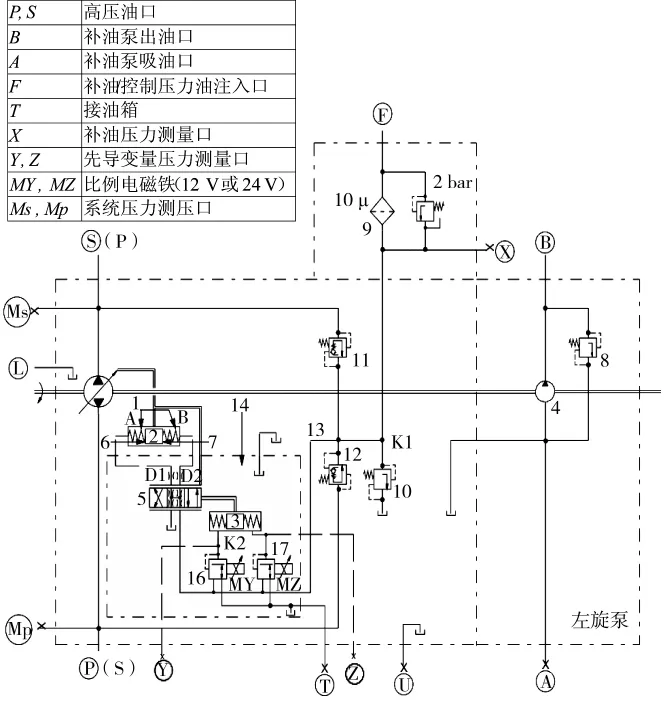
图1 变量泵原理图

比例电磁铁将电流信号转换成位移信号，其线圈电流动态过程用微分方程表示为：

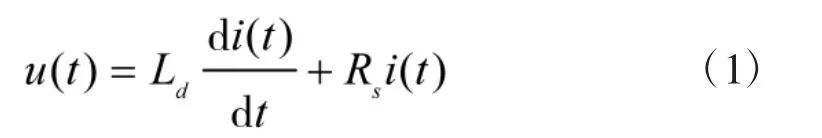
对式（1）进行拉式变换可以得到：

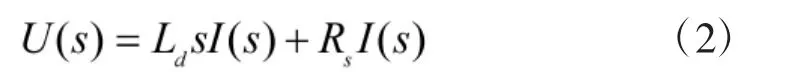
整理得到：

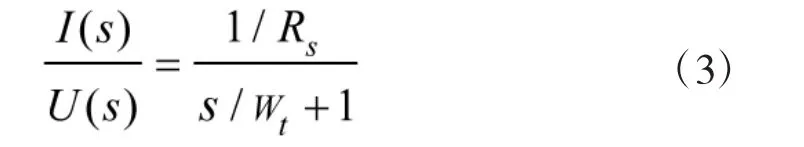
式中，Wt=Rs/Ld，Ld为线圈动态电感；Rs为线圈和比例控制放大器内阻。

伺服阀的功能是将比例电磁铁的输出功率进行放大，被用来控制液压缸。本文将伺服阀控制流量与电路中桥式回路进行类比［10］，看成液阻构成的无源网络。阀口的变化将影响控制回路的流量和压力。建模时将滑阀看成两个可变液阻差动连接的全桥，如图2所示。

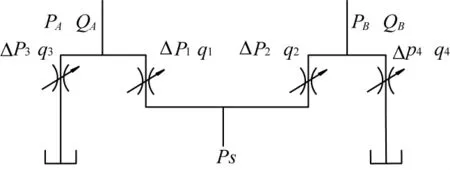
图2 A型液压全桥示意图

比例电磁铁通电后，电磁铁的输出力为伺服阀的输入信号，伺服阀的阀芯位移为输出量。

伺服阀的微分方程为：

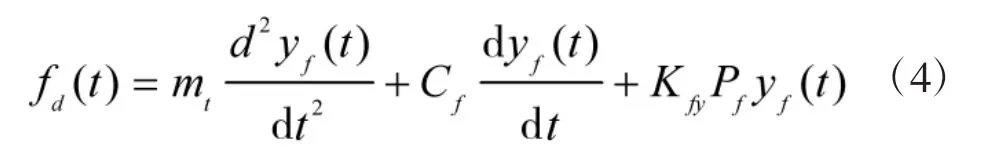
对式（4）进行拉氏变换可得到：

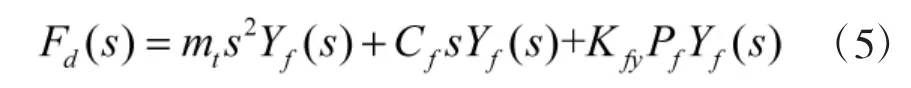
整理得到：

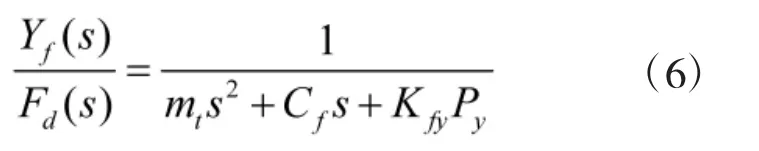
式中，mt为伺服阀芯组建的质量；Cf为伺服阀芯的动态阻尼系数；Pf为控制油压力；Kfy为液动力等效刚度；fd（t）为电磁铁的输出力；yf（t）为伺服阀芯位移。

由于阀控液压缸建模过程比较复杂，这里给出几个重要的推导公式。

伺服阀流量方程的线性化方程拉式变换后为：

液压缸流量连续性方程拉式变换后为：

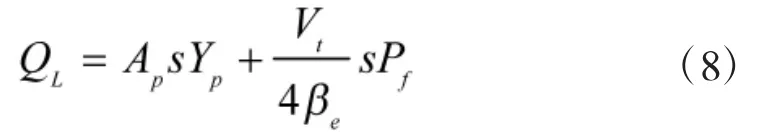
液压缸输出作用力与所受斜盘和弹簧的反作用力的动态平衡方程拉式变换后为：

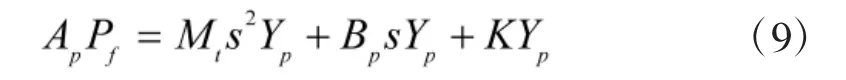
联立式（7）～式（9）得阀控液压缸的传递函数为：

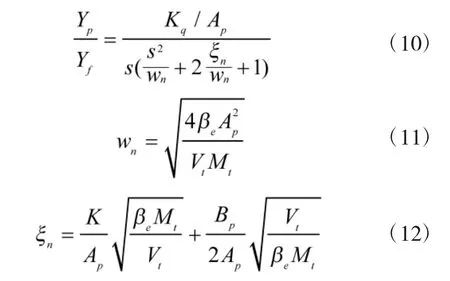
式中，Yf为伺服阀芯位移；Yp为活塞位移；Ap为活塞有效面积；βe为液压油体积弹性模量；Vt为液压缸有效容积；Mt为活塞总质量；Bp为粘性阻尼系数；K为负载弹簧刚度。

根据以上分析可以得到变量泵变量调节机构的回路框图如图3所示。

综合上式可以得到变量泵的流量方程为：

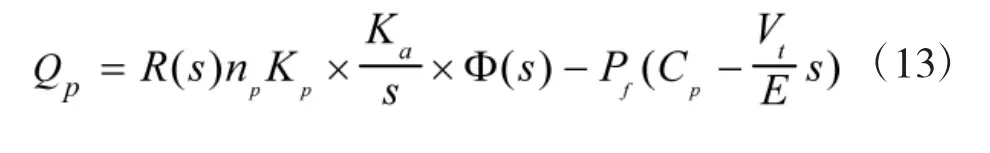
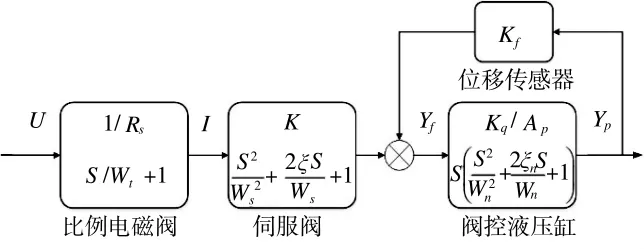
图3 变量泵调节机构回路框图

本文保持系统恒转速输出的主要思路为：根据变量泵的流量方程，通过非线性PID控制变量泵流量始终维持在稳定状态，从而达到定量马达输出转速恒定的目的。

2 恒转速输出的非线性PID控制

传统的PID控制方法广泛应用于工业控制领域，其控制原理是基于误差来生成消除误差的控制，优点为依靠控制需达到的目标与实际行为之间的误差来确定消除此误差的控制策略。但传统的PID控制不能同时很好地满足稳态精度与动态稳定性、平稳性与快速性的要求。对于类似本课题研究对象，即存在强非线性，快速时变不确定性以及强干扰特性的对象控制效果较差。

相比于常规PID控制器，非线性PID控制器的控制思路是使用非线性跟踪器来产生新的控制要素，并利用这些新要素的非线性组合方式改进传统PID调节器，使其适应性和鲁棒性得以大幅度提高。它对输入信号处理并对测量信号滤波后，利用非线性PID控制器产生新的控制量，可根据不同的情况改变比例增益Kp、积分增益KI、微分增益KD的大小，对非线性系统能取得更好的控制效果［11］。因此，本文通过对PID控制器各参数期望变化规律的研究，引入一种非线性机制，以用于变量泵恒流量控制。

2.1 恒转速输出的PID控制表达式

由方案设计得知，可以通过控制变量泵的流量恒定来保持输出转速的恒定。根据变量泵给定的目标流量QSet（k）和实际流量QSensor（k）构成的流量偏差e（k）=QSet（k）-QSensor（k），恒转速输出的非线性PID控制表达式为：

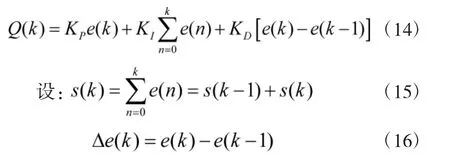
式（14）可以表示为：

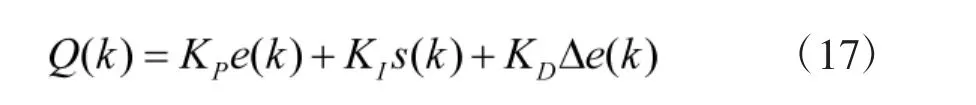
其中，各项增益控制为非线性比例系数，详细介绍如下。

2.2 比例增益控制规律

比例控制可以加快系统响应时间，减少调整时间，然而KP的增加会使系统的稳定性下降。系统开始阶段（或从稳态进入暂态阶段），此时系统偏差E（t）、偏差变化率 EC（t）变大，增益 KP应该变大；在动态阶段，此时 E（t）、EC（t）较于先前阶段会变小，增益KP也应该越来越小。在稳态阶段，E（t）、EC（t）非常小，增益KP应该保持一个很小值。根据上面分析可以引入KP的非线性函数为：

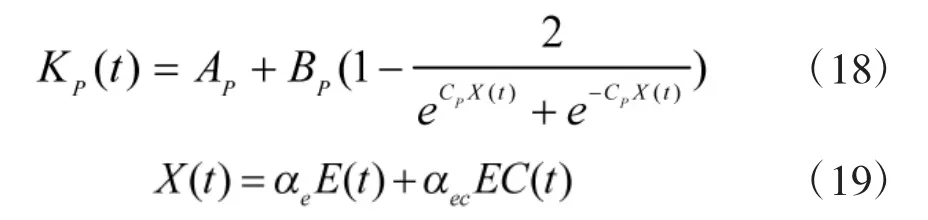
式中，αe、αec为加权系数。为了调整偏差和偏差变化率的加权值，引入以下加权机制：

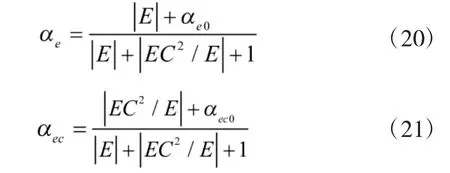
式中 AP、BP、CP为由变量泵决定的常数，αe0+αec0=1。KP随 E（t）、EC（t）的变化规律如图4所示：

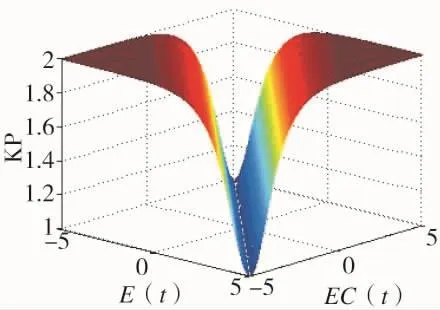
图4 KP变化曲线

2.3 积分增益控制规律

积分控制能使系统无静差，KI越大，积分作用越强，动态响应速度越快，但KI过大可能会使系统不稳定。系统开始阶段（或从稳态进入暂态阶段），KI应随 E（t）、EC（t）的变大而减小；在动态阶段，此时KI应随着 E（t）、EC（t）变小而增大；在稳态阶段，E（t）、EC（t）非常小，KI应保持为一个较大值。根据上面的分析可以引入KI的非线性函数为：

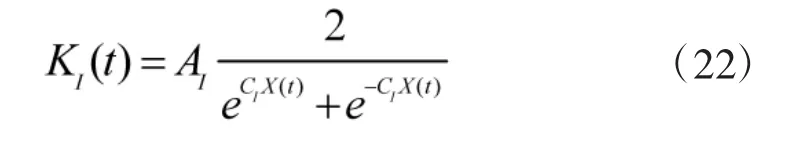
式中，AI、CI为变量泵决定的常数，KI随 E（t）、EC（t）的变化规律如图5所示。

2.4 微分增益控制规律

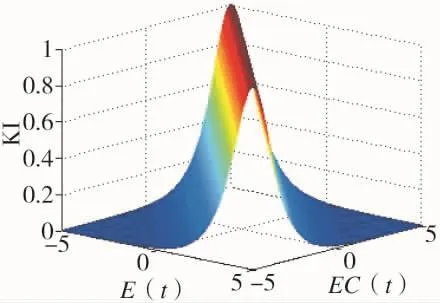
图5 KI变化曲线

微分控制能提高系统的动态响应速度，但是在E（t）=0 时微分控制会放大噪声。当系统 E（t）、EC（t）变大时，KD应随之增加；当系统 E（t）、EC（t）变小时，KD应随之减少；在系统稳态阶段，KD维持为一个极小值。根据上面的分析可以引入KD的非线性函数为：

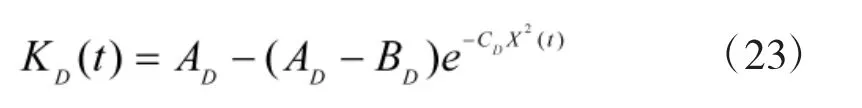
式中，AD、BD、CD为变量泵决定的常数，KD随 E（t）、EC（t）的变化规律如图6所示。

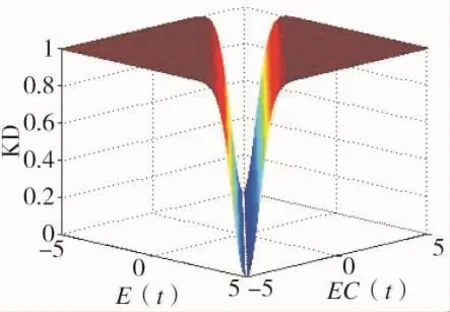
图6 KD变化曲线

2.5 PID控制表达式与变量泵的流量方程结合

由式（13）与式（17）结合可知：

得出变量泵流量方程的非线性PID控制表达式为：

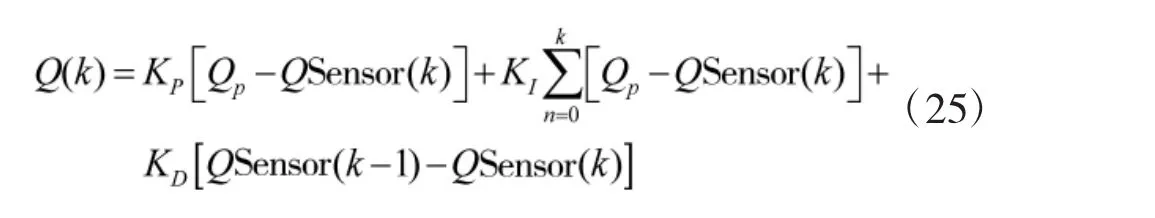
比例、积分、微分参数对系统性能影响是相互联系的，以上列举了对各参数分开讨论的情况，并将之整合为统一的变量泵流量方程的非线性PID控制表达式，由以下实验加以验证。

3 基于FPGA/SOPC的泵控马达控制系统设计

FPGA是现场可编程门阵列（Field Programmable Gate Array）的简称，具有高速率、多功能、设计灵活、可现场调试验证等优点，可以处理数据量大、计算复杂的运算。SOPC是可编程的片上系统技术（System on Programmable Chip）的简称，是Altera公司提出来的一种灵活、高效的基于FPGA的SOC解决方案，可以将嵌入式处理器、DSP、存储器、I/O等外围设备集成到FPGA芯片内。本文采用“SOPC+FPGA架构”技术设计了泵控马达恒转速控制系统，主要包括SOPC系统模块、算法处理模块与非线性PID控制器模块。使用传感器采集变量泵的流量与定量马达的转速，数据经A/D转换器输入FPGA，通过Avalon总线存储到SDRAM和传输到算法处理模块，得出的参数值送入非线性PID控制器模块，最后由非线性PID控制器模块输出PWM控制波驱动变量泵。整体框图如图7所示。

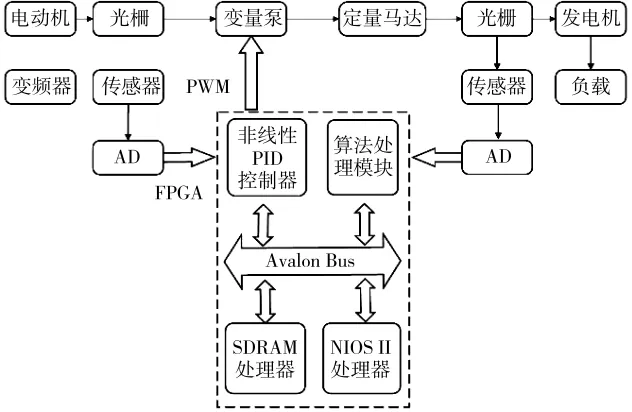
图7 泵控马达控制系统框图

4 实验结果分析

变量泵选择林德公司的HPV105-02E1型电液比例控制变量泵和型号为HMF50-02的定量马达。FPGA芯片选择Altera公司的EP2C70F6，该芯片具有数据处理速度快，能耗较低的特点。由于FPGA芯片的控制电压为3.3 V，而电磁比例阀的控制电压为24 V，所以需要控制信号放大电路放大PWM波。

系统本身的一些参数（比如泄漏系数等）对由变量泵控定量马达组成的泵控马达系统的输出转速影响较小，可以忽略不计。对系统输出转速稳定影响较大的参数有两部分，分别是变量泵输入转速的时变因素和系统负载的突变因素，所以本文分别测试了这两种情况下系统的输出转速。

4.1 变量泵输入转速时变情况测试

测试变量泵输入转速分别为800 r/min和1 500 r/min情况下突加和突减300 r/min时马达的转速波动情况，如图8所示。

从图中可以看到输入转速变大，转速波动变小，最大为30 r/min，超调量最大为2%，调整时间最大为1.5 s。即可得出在变量泵输入转速变化时，马达转速波动范围较小，基本保持匀速，说明本文设计的恒速控制器能很好地控制系统。

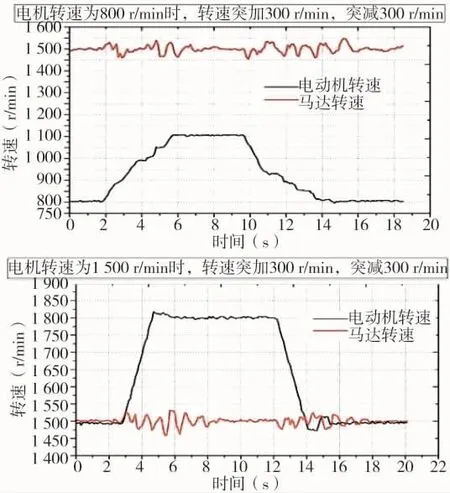
图8 输入转速时变时马达转速变化曲线

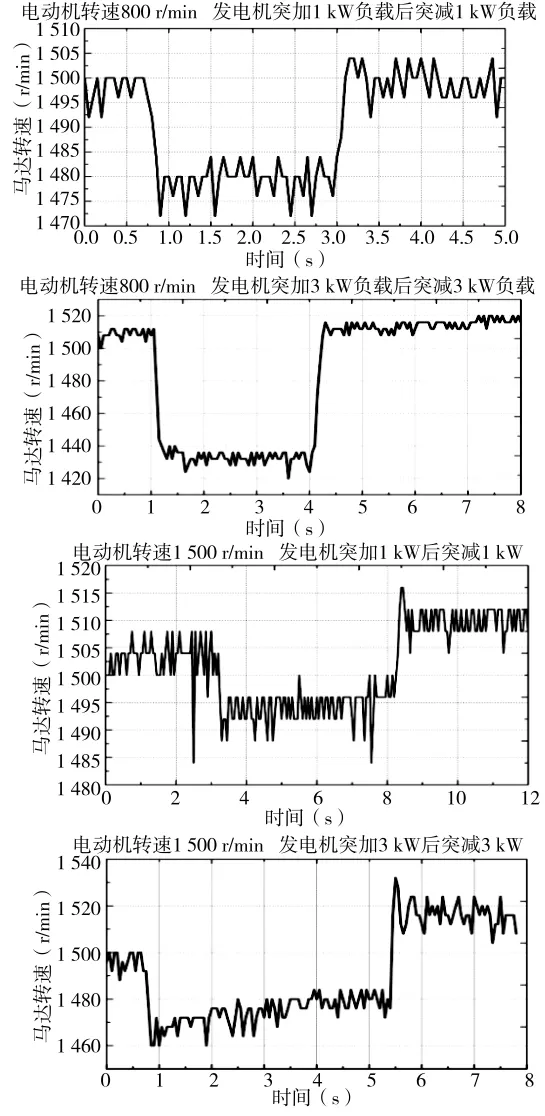
图9 负载突变时马达转速变化曲线

4.2 系统负载突变情况测试

当变量泵输入转速分别为800 r/min和1 500 r/min时，利用按键调节占空比将马达转速调节到1 500 r/min，并分别测试各组突加突减1 kW、3 kW负载情况下马达的转速波动情况，如图9所示。

实验结果表明，随着负载突变增加，马达转速减少，马达转速波动量增加，转速波动量最大可达40 r/min，超调量最大为2.6%，调整时间最大为1.8 s。负载减少后马达转速增加，最大波动量可达60 r/min，超调量最大为3.5%，调整时间最大为2 s。在变量泵输入转速增加时，马达的速度降落和上升均比较快，最长时间不超过200 ms，在突减负载的情况下马达转速上升范围比下降范围要大。

5 结论

通过建立变量泵流量方程，采用非线性PID算法解决泵控马达系统输出转速的非线性波动问题，可以得出以下结论：1）系统负载恒定时，变量泵输入转速越高，系统对转速突变的承受能力越强，高速输入时转速突变情况下马达输出转速波动较小，但是响应时间增长，震荡次数增加。2）负载突变对系统的影响比较明显，负载变化越大，马达输出转速波动越大，系统震荡次数增加，系统更难保持稳定。3）非线性PID控制算法能够很好地解决输入转速时变和负载突变情况下马达输出转速波动问题，对于输入转速时变问题效果尤为明显。