基于CWLS时差频差无源定位闭式解算方法*

冯 奇，曲长文，周 强，郭林鹏

（海军航空大学，山东 烟台 264001）

0 引言

无源定位是一种观测设备自身不辐射信号，仅通过接收目标电磁信号来估计目标状态的技术。相对于雷达、声纳等有源探测技术，无源定位系统［1］具有生存能力强、侦察作用距离远、能够有效应对隐身目标等优点。无源定位的本质就是通过优化求解观测方程获得目标状态估计［2］。

时差（Time Difference of Arrival，TDOA）、频差（Frequence Difference of Arrival，FDOA）与目标状态的非线性关系很强，导致其观测方程不能直接进行伪线性处理［3］，需要借助中间变量。对此文献［4］利用球面插值（Spherical Interpolation，SI）法推导了观测方程的伪线性形式，然后利用线性最小二乘（Least Squares，LS）估计目标位置。文献［5-6］改进了SI法，考虑了伪线性方程中误差项的统计特性及目标状态与中间变量之间的关系，在此基础上提出了两步加权最小二乘（Two-Stage Weighted Least-Squares，TS-WLS）算法。文献［7］进一步将此类伪线性定位方法抽象归纳，提出一种基于加权最小二乘（Weighted Least-Squares，WLS）的定位理论模型。但是由于WLS运算中回归量以及回归附属量之间的误差相关性导致此类WLS算法的状态估计是有偏的［8］。

针对WLS估计有偏的问题，文献［9］中讨论了基于CWLS的无源定位闭式解算理论框架。本文将该理论框架应用于TDOA/FDOA无源定位场景，在TS-WLS基础上提出一种基于CWLS的TDOA/FDOA无源定位闭式解算方法。通过理论分析证明了本文算法在保持了TS-WLS算法定位精度基础上，有效减小了目标状态估计偏差。

1 定位模型

不失一般性，考虑多运动观测站对运动目标的TDOA/FDOA无源定位场景。显然，TDOA定位就是该场景中观测站与目标速度为零的情况下的一个特例，因此，本文结论完全适用于TDOA无源定位算法。

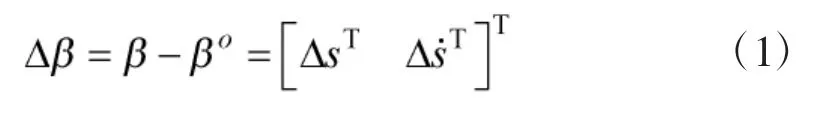
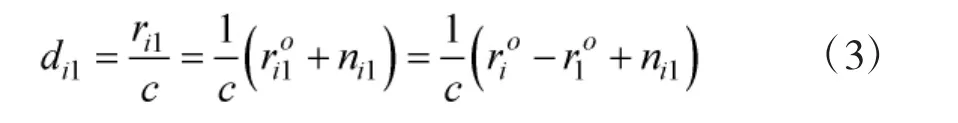
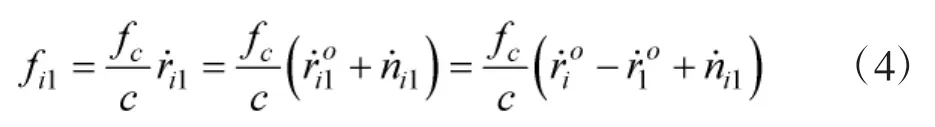
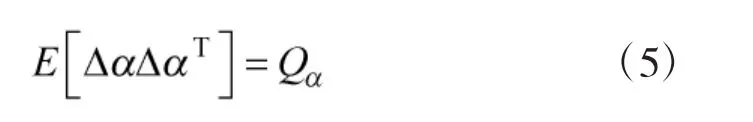
2 CWLS定位算法

本文算法在TS-WLS算法框架基础上改进，第1步中使用CWLS算法代替WLS算法，在保持WLS算法定位精度的基础上，有效减小估计偏差，下面给出基于CWLS的定位模型。

第1步：TDOA/FDOA无源定位体制的观测方程借助中间变量进行伪线性化处理得

式（7）中，0m×1表示m行的零向量。WLS算法通过选择使下式最小化的t作为估计值

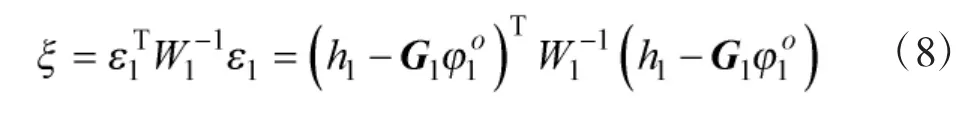
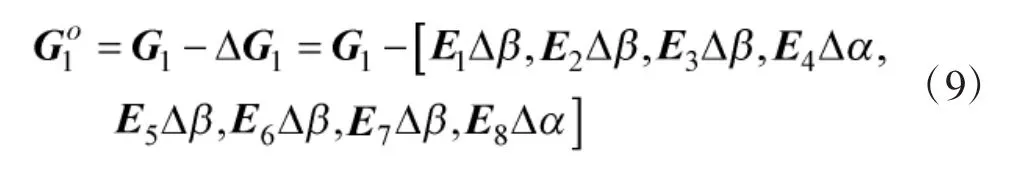
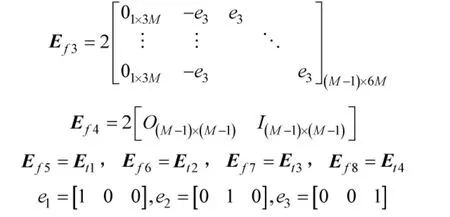
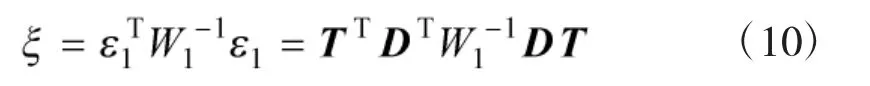
同上，将向量h1表示为确定矩阵与噪声向量乘积的形式，可得

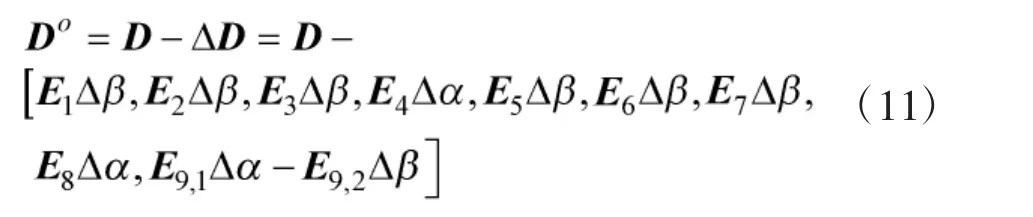
将式（11）带入式（10）得

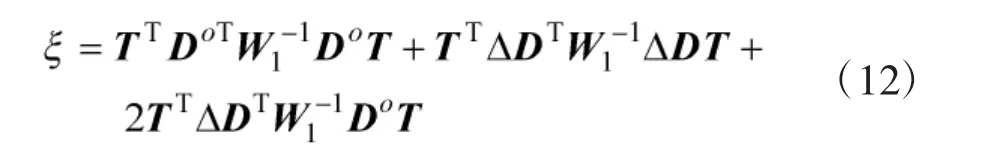
其中，误差项ΔD是零均值的，因此，对式（12）两边求均值得

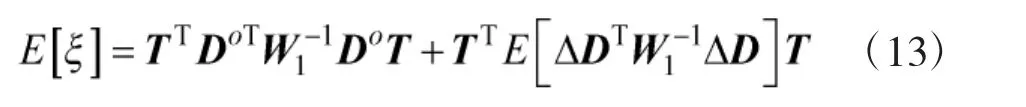
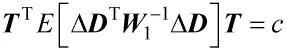
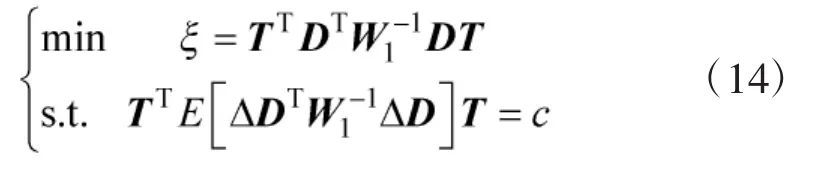
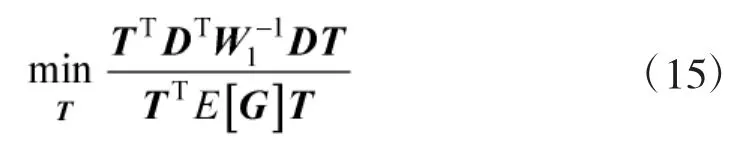
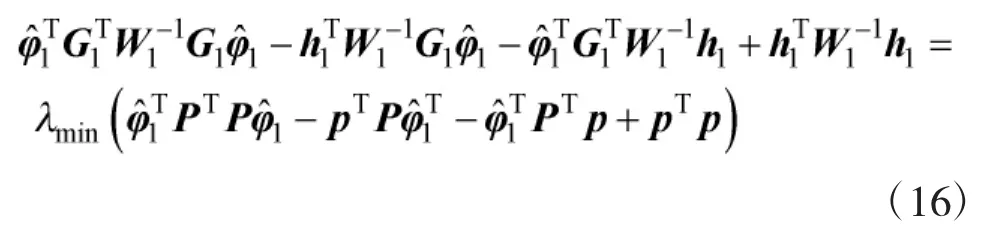
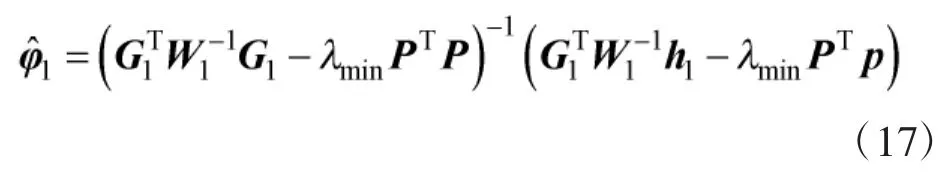
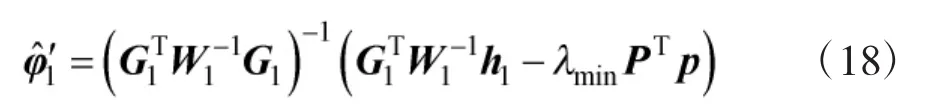
将式（18）代入式（17）得

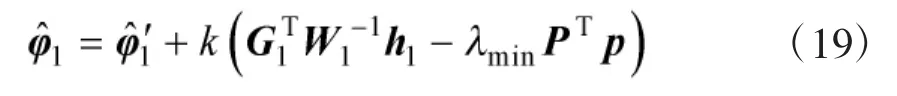
估计误差可以表示为

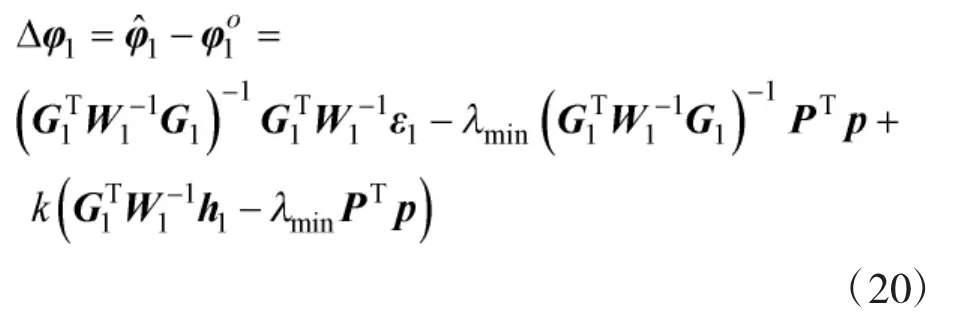
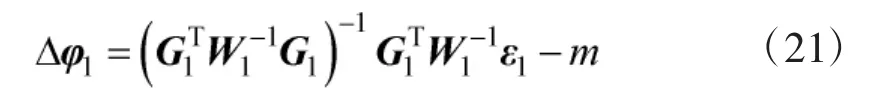
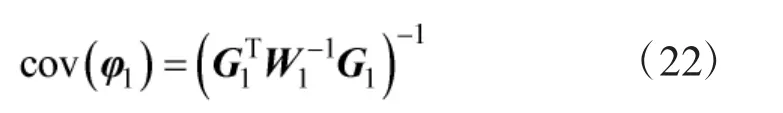
至此，第1步结束，第2步与TS-WLS算法完全相同。综上，所提基于CWLS的闭式解保持了与TS-WLS算法相同的定位精度。文献［5］给出了TS-WLS目标状态估计MSE的具体表达式，且证明了其渐近有效性，本文不再赘述。

下面根据前面的推导及分析给出算法的实现步骤：

1）借助中间变量对TDOA/FDOA无源定位方程进行伪线性化处理，构造扩维系数矩阵D。

2）将扩维系数矩阵D每一列表示为系数矩阵与误差向量乘积形式，如式（11）所示。

3）令权重矩阵W1=Qα，计算得到矩阵和 E［G］。对矩阵束进行广义特征值分解，选取最小特征值min对应的特征向量作为选择向量，则目标状态向量估计值。

4）利用步骤3）中目标状态粗估计值，求得精确的权重矩阵W1。重复步骤3）得目标状态精估计值，第1步结束。

5）第2步与TS-WLS算法相同，进一步提高定位精度。

需要说明的是，TS-WLS算法第2步中系数矩阵G2为常系数矩阵，不能将每一列表示为系数矩阵与误差向量的乘积形式，因此，无法应用本文算法优化。

3 算法分析

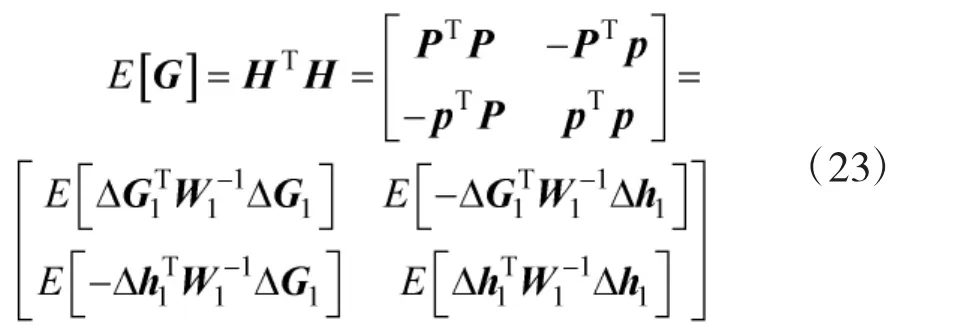
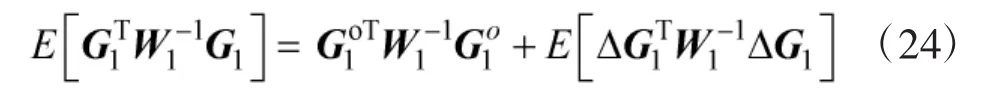
综合式（23）、式（24）可得

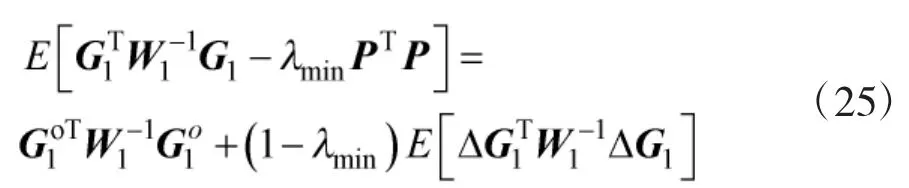
同理，可得

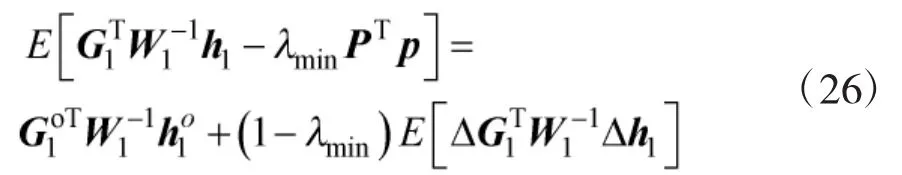
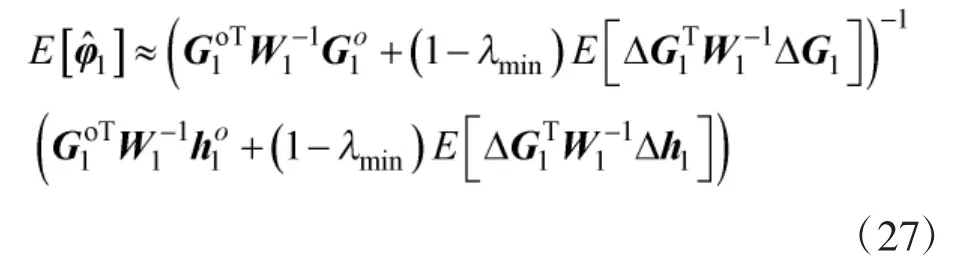
由式（17）可得，本文算法闭式解是通过对WLS估计值进行双边补偿得到的。综合式（25）～式（27）可得本文所提闭式解定位偏差小于WLS估计值偏差，具有减小定位偏差特性。

4 仿真分析

本节对TDOA/FDOA无源定位体制进行数据仿真，将本文算法与文献［5］所提TS-WLS算法及CRLB进行性能比较。

观测站状态参数真值如表1所示。观测时刻目标位置为（2000m 2500m 3000m），运动速度为（-20 m/s 15 m/s 40 m/s）。观测站位置测量误差方差取。各观测站站址测量误差不同，且相互独立，观测站的站址误差协方差矩阵

式中：diag（·）表示以其中元素为对角线的对角矩阵。观测站速度测量误差协方差阵。TDOA、FDOA测量误差服从零均值高斯分布，且相互独立。

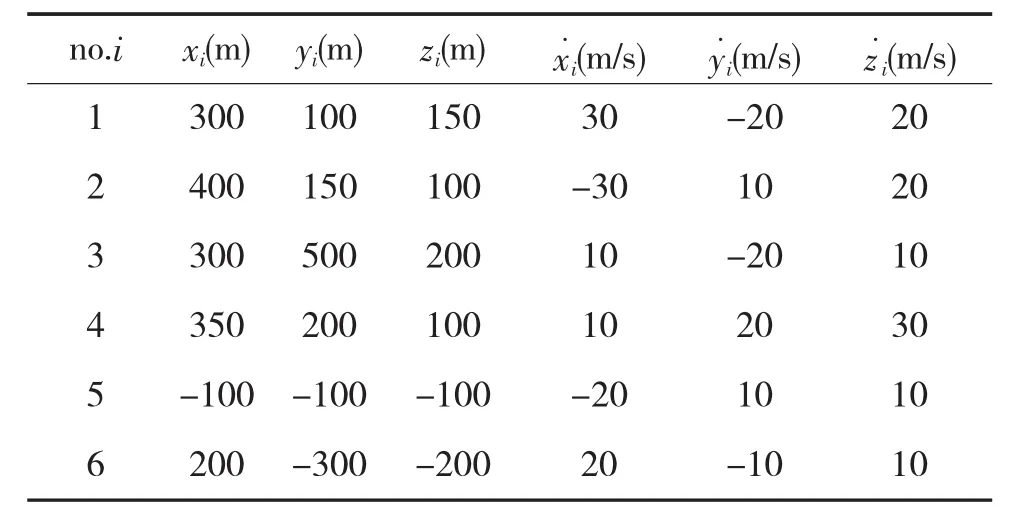
表1 观测站状态参数

4.1 TDOA/FDOA无源定位

在TDOA/FDOA无源定位场景中，从定位精度和估计偏差两方面，对本文所提基于CWLS的闭式解与TS-WLS算法进行比较。图1分别给出假定FDOA测量误差标准差aFDOA=-30 dB情况下，目标位置和速度估计MSE随着TDOA测量误差的变化曲线；图2分别给出假定TDOA测量误差标准差aTDOA=-30 dB情况下，目标位置和速度估计MSE随着FDOA测量误差的变化曲线。仿真中目标状态估计MSE定义表达式为

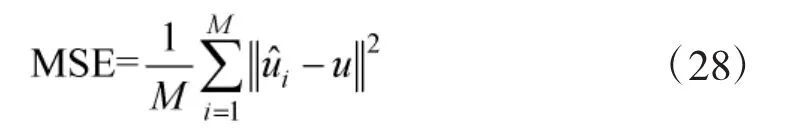
式（28）中，M表示Monte Carlo仿真实验次数，仿真中取M=2 000。

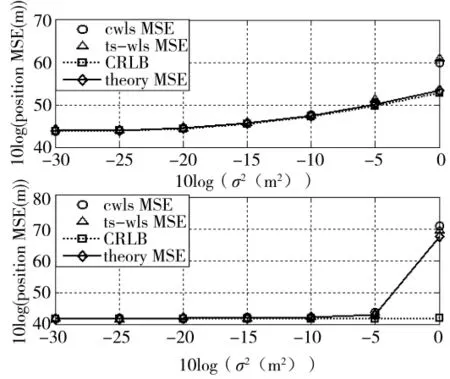
图1 目标状态估计MSE随TDOA测量误差变化曲线

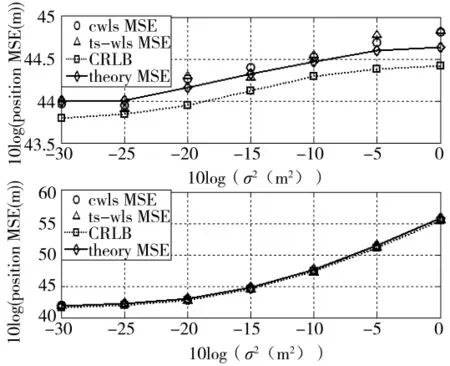
图2 目标状态估计MSE随FDOA测量误差变化曲线

由图1可得本文所提基于CWLS算法闭式解基本保持了与TS-WLS算法相同的定位精度，且均能较好地逼近CRLB，符合第2节对CWLS闭式解估计误差的分析，由图2可以得到同样的结论。值得注意的是，图1中目标速度估计的CRLB不随着TDOA的测量误差变化而变化，这是因为TDOA参数中不包含目标的速度信息而导致的。图2中目标的位置估计CRLB随着FDOA的测量误差变化而变化，这是因为FDOA参数中既包含了目标的速度信息，也包含了目标的位置信息。

下面比较TDOA/FDOA无源定位中本文所提基于CWLS算法闭式解与TS-WLS算法的估计偏差特性。图3分别给出假定FDOA测量误差标准差aFDOA=-30 dB情况下，目标位置和速度估计偏差随着TDOA测量误差的变化曲线；图4分别给出假定TDOA测量误差标准差aTDOA=-30 dB情况下，目标位置和速度估计偏差随着FDOA测量误差的变化曲线。仿真中目标状态估计偏差［12］定义式为

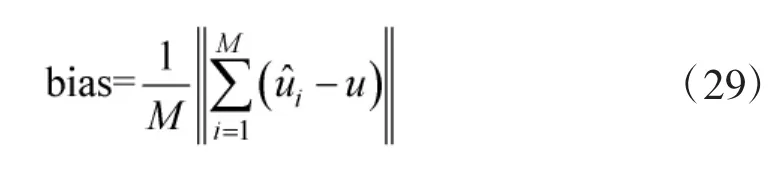
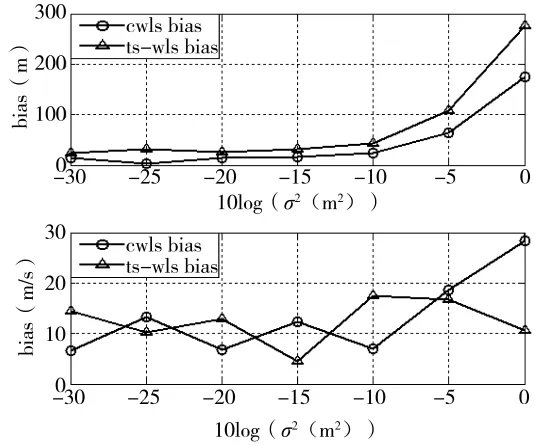
图3 目标状态估计偏差随TDOA测量误差变化曲线

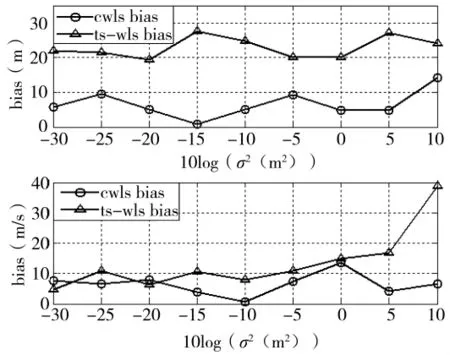
图4 目标状态估计偏差随FDOA测量误差变化曲线

由图3可得随着TDOA测量误差变化，本文所提基于CWLS算法闭式解的目标位置估计误差明显小于TS-WLS算法，当TDOA测量误差强度达到0 dB时，基于CWLS算法闭式解的目标位置估计偏差能减小大约100 m。由于TDOA参数中不包含目标速度信息，因此，两种算法的速度估计误差偏差差别不明显。由图4可得随着FDOA测量误差变化，本文所提基于CWLS算法闭式解的目标速度估计误差基本保持比TS-WLS算法小的趋势。同上述分析，由于FDOA参数中同时包含了目标速度信息和位置信息，因此，图4中本文所提基于CWLS算法闭式解的目标位置估计偏差明显小于TS-WLS算法，且差值比较恒定，大约为16 m左右。

5 结论

本文在TS-WLS算法基础上提出一种基于CWLS的TDOA/FDOA无源定位闭式解算方法。给出了该闭式解的解析表达式，并推导了目标状态估计的MSE。数据仿真结果表明本文所提算法与TS-WLS算法具有相同的定位精度，均能较好地逼近CRLB，而且所提算法的目标状态估计误差明显小于TS-WLS算法，验证了理论分析的正确性。