基于粒子滤波的多异步传感器检测前跟踪算法

2019-06-15杜郑成陈华杰王圣哲

火力与指挥控制 2019年1期

杜郑成，陈霄，陈华杰，王圣哲

（杭州电子科技大学通信信息传输与融合技术国防重点科学实验室，杭州 310018）

0 引言

在低信噪比的复杂环境下，雷达探测系统对弱目标的检测跟踪问题一直都是一项技术难题［9］。检测前跟踪（Tracking Before Detection，TBD）是一种可以提高传感器当目标在低信噪比环境下检测概率的方法，它在进行检测的过程中加入跟踪的思想，并且降低对目标的检测门限，然后再通过对目标原始能量的积累来进行目标检测，常用于对微弱目标信号的检测［1］。目前的TBD方法主要有Hough变换［2］、动态规划（Dynamic Programming，DP）［3］及粒子滤波（Particle Filter，PF）［4］。动态规划法计算简单，但对于低信噪比情况，需要经过长时间积累处理，而基于PF的TBD方法由于其实时性和处理非线性非高斯问题的能力而受到广泛关注。基于PF的TBD算法首先由Salmond［4］于2001年提出，其后，许多学者做了相关研究，如 Rutten［5］、Y.Boers［6］和 Hlinomaz［7］等。

现在已有的关于粒子滤波检测前跟踪的算法主要研究的问题是关于单传感器方面的，在多雷达目标检测跟踪方面的研究非常少。但是在实际情况下，一般都是通过多个传感器对目标进行联合探测，然后根据各个传感器之间的探测信息的互补性来提高目标正确发现概率和跟踪效果。但是当融合多个传感器信息的时候，因为雷达采样时刻不同，多部传感器对相同目标的量测并不是目标处于同一位置的量测，如果直接将这些量测信息进行融合，最后得到的结果会有很大的误差。

本文针对单目标检测跟踪问题提出了基于粒子滤波的多异步传感器检测前跟踪算法，这种算法将粒子的权重和雷达回波信息相关联，通过对粒子的状态进行时间和空间递推，将雷达对于目标位于不同时刻的回波幅值映射到同一个粒子的权重中，然后再对粒子及粒子权重进行融合，这样就可以达到对多雷达的回波幅值信息进行融合的目的，由于杂波和目标的权重值有着明显的差别，这样就可以区分出目标和杂波，从而获得目标航迹。同时，为了减少计算量，将粒子群根据分布和权重不同，仅选用部分对于目标位置估计影响大的粒子进行空时校准。

1 目标模型与量测模型

1.1 目标运动建模

假设有多个雷达对同一个区域进行探测，在该区域中有单个目标在xy平面运动。目标运动模型和观测模型描述如下：

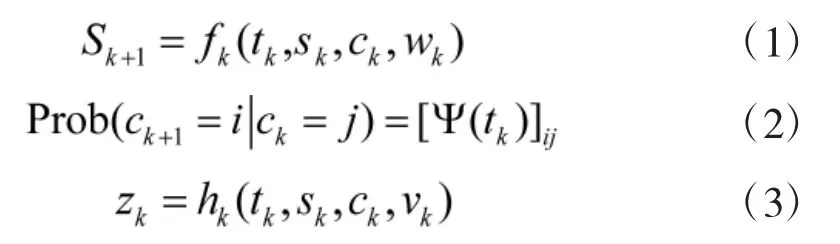
式中，用ck来表示模型变量，通过这个模型变量来表示目标是否出现；Ψ（tk）是马尔可夫状态转移矩阵。模型之间的状态转移概率通过Ψ（tk）来完成。vk是目标的过程噪声。

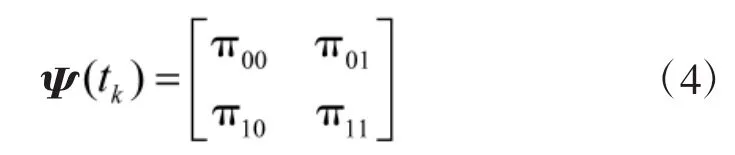
1.2 传感器量测建模

设有L个雷达同时检测某一个区域，这些雷达的采样周期相同但是系统误差各不相同［13］。假设第i个雷达在k时刻产生一系列距离—方位图像，其中每帧图像包含Nri×Nbi个分辨单元，将每个分辨单元设为（m，n），m=1，2，…，Nr，n=1，2，…，Nb，对应一个矩形区域［13］。则雷达i在时刻k的观测数据可以表示为：

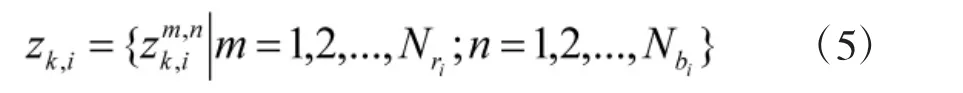
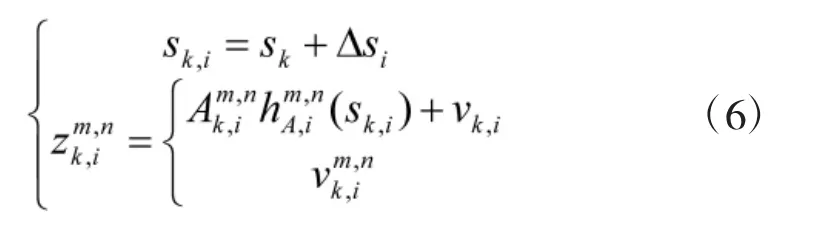
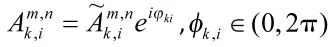
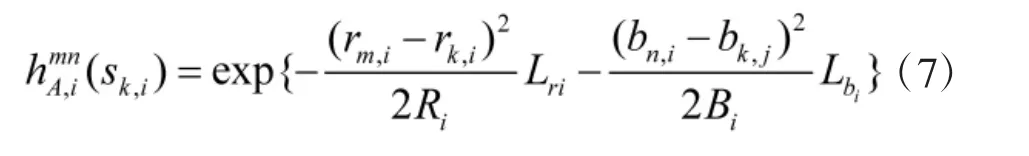
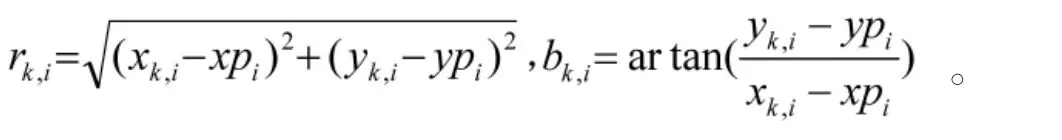
式中，nIk，i和 nQk，j是均值为零，方差为 an2的高斯白噪声，并且相互独立。信噪比为，。

k传感器i获取的观测可以表示为：

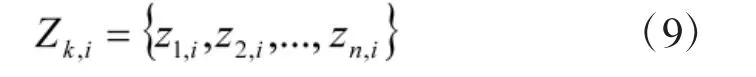
在式中用Zk，1∶L来表示在k时刻全部的雷达观测数据。

2 多异步传感器检测前跟踪算法

2.1 单传感器检测前跟踪算法基本步骤

已知粒子集初始分布p（s0，r0），粒子数为 M。

步骤1首先将粒子集的初始权重设置为1/M，n=1，…，M，采样。

步骤3计算有效样本数 Neff，若 Neff＜NT，则进行重采样，之后将粒子集的各个权重值重新设置为初始值1/M。

步骤4按照式（4）估计目标状态。如果把时刻k的粒子进行过重采样，重采样之后所对应目标其存在的粒子数为R，那么它的目标检测概率表示为Prk=1=R/M。

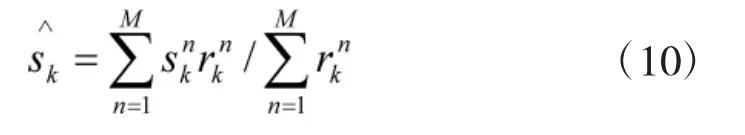
2.2 基于粒子滤波的多异步传感器检测前跟踪算法

本文算法是在基于粒子滤波的单雷达检测前跟踪算法的基础上，通过融合同一粒子对应于不同雷达的权重值，将多个异步雷达的量测信息进行融合，实现基于粒子滤波的多异步传感器检测前跟踪。算法首先在多个传感器的共同探测区域，产生初始粒子群。然后根据先验信息确定基准雷达，以基准雷达的采样时刻作为基准时刻。对于每一个粒子，根据不同雷达的采样周期与基准时刻的时间差和粒子当前状态，对粒子的状态进行时间校准，获得该粒子对应于不同雷达的虚拟粒子。根据雷达的量测回波信息和对应的虚拟粒子的状态，计算得到粒子对应于每个雷达（包括基准雷达）的权重值。最后将粒子各个不同权重相乘得到融合后的权重，并且把融合后得到的权重值归一化。之后再对粒子重采样处理，并且估计出目标的存在概率和状态。

具体实现步骤如下：

已知粒子集的初始分布p（s0，r0），粒子数取为M。

步骤2根据式（1）对粒子状态更新。

步骤3权值计算。由于多个雷达获得的是目标在不同位置的回波信息，这样直接计算得到的粒子j的各个权重是不能直接相乘融合的，所以需要以其中一个雷达的时刻作为基准雷达。假设以雷达1的时刻作为基准时刻，然后将其余雷达i=1，…，N对粒子j相对应的时刻的状态通过式（11）分别对x坐标和y坐标进行时间回推，公式如下：

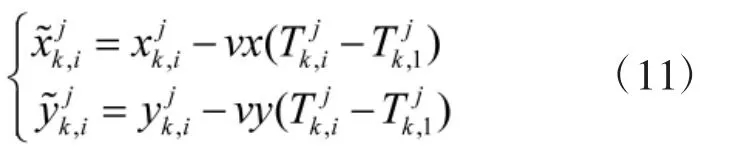
将粒子j对应于雷达i通过时间和空间回推到基准时刻后，所对应的状态变量可以表示为：

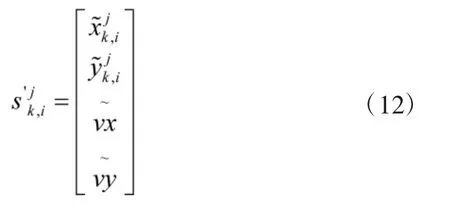
计算相应的权重，权重计算公式如下：

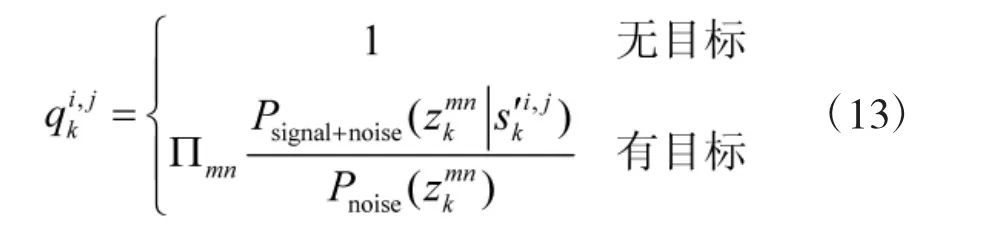
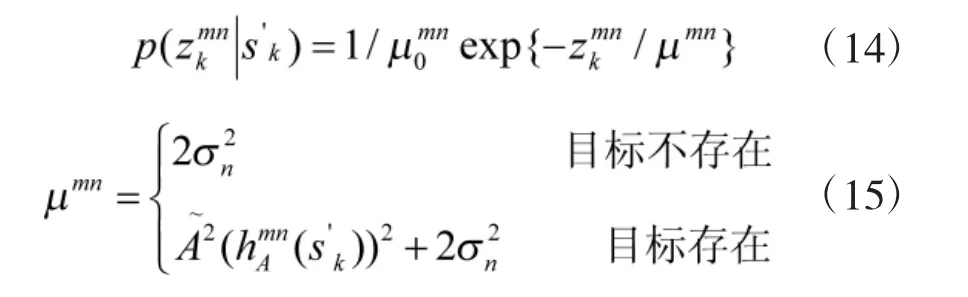
然后将粒子j对应不同雷达i的权重相乘得到融合后的权重qkj，公式如下：

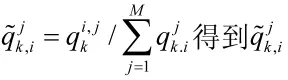
步骤4判断是否重采样。若有效样本数Neff＜NT，则重采样，并将粒子各权重重新设置为1/M，其中NT表示阈值。

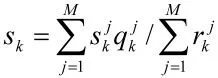
3 仿真实验

假设在多个传感器的探测区域内，有目标分别做匀速直线运动和匀加速直线运动。在仿真环境中，设置仿真时间为40 s，设定目标在第5 s出现，第 30 s消失，目标初始位置为（13.8，3）km，初始速度为（-0.1，-0.2）km/s。若目标做匀加速直线运动时，ax为x轴方向加速度，ay为y轴方向加速度，均设为-0.008 km/s2。雷达数目L=2，其坐标位置分别为（0，3）km 和（2，-4）km，并在［5，15］km 和［-π，π］rad范围内分别生成的距离—方位图像，包含40×40 和 30×30个单元，T=1 s，取 an=0.5。

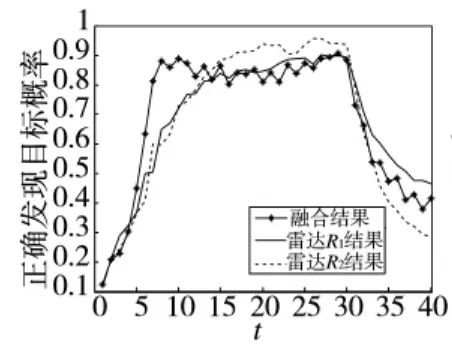
图1 信噪比5的目标正确发现概率

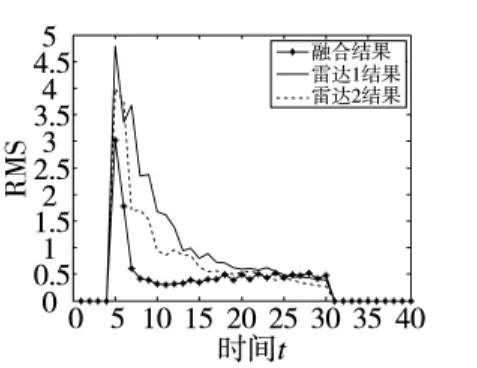
图2 信噪比5的目标位置估计RMS比较结果

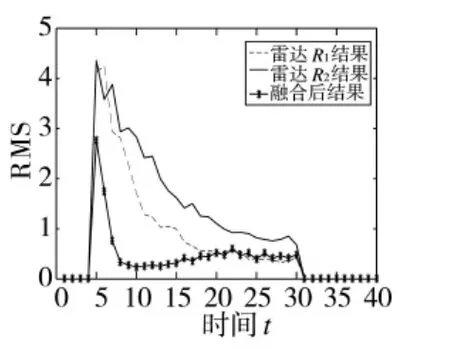
图4 信噪比9的目标位置估计RMS比较结果

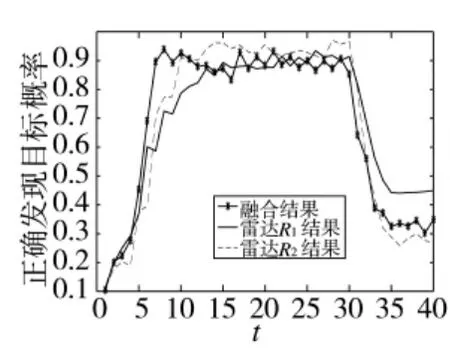
图5 信噪比12的目标位置估计RMS比较结果

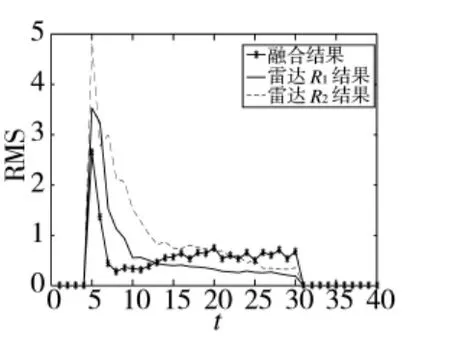
图6 信噪比12的目标正确发现概率

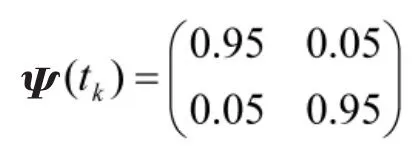
由图2可见，利用本文算法对两部雷达的量测信息进行融合后，与单个雷达的检测跟踪结果相比，融合后得到的目标精度得到明显改善，在第5 s目标出现时，跟雷达1相比，本文算法的误差降低了10%，与雷达2比较，降低了17%。之后融合后的误差急剧减小，在第10 s的时候误差仅为2.5%，而此时雷达1和雷达2的误差分别为9%和16%。在第7 s的时候效果最为明显，与雷达1相比，本文算法的误差降低了12%，跟雷达2相比降低了29%。当跟踪稳定后，融合后的误差稳定在5%左右，与雷达1和雷达2的误差基本保持相同。

图3、图4分别为信噪比为9，即P=2.7，Q=0.3情况下的目标正确发现概率图和RMS比较图。图5、图6为信噪比为12，即P=3.6，Q=0.3情况下的目标正确发现概率图和RMS比较图。由图可知，本文算法可以有效降低误差和提高目标正确发现概率。

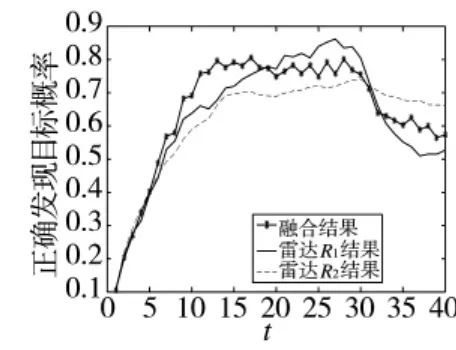
图7 信噪比5的目标正确发现概率

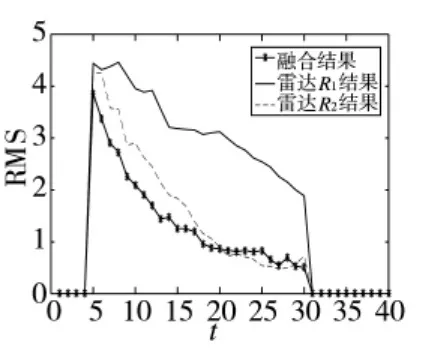
图8 信噪比5的目标位置估计RMS比较结果

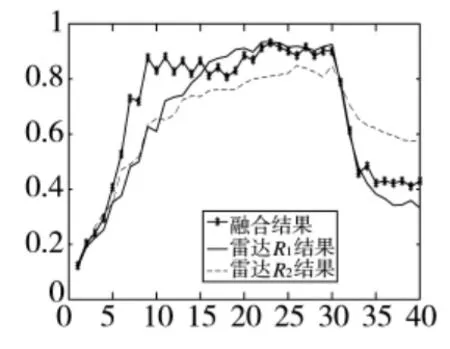
图9 信噪比9的目标正确发现概率

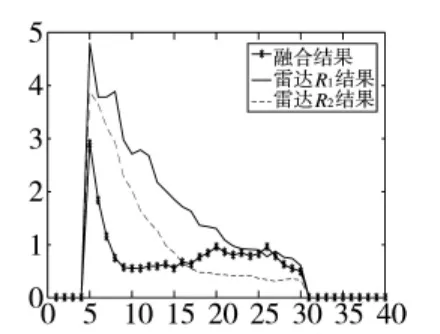
图10 信噪比9的目标位置估计RMS比较结果

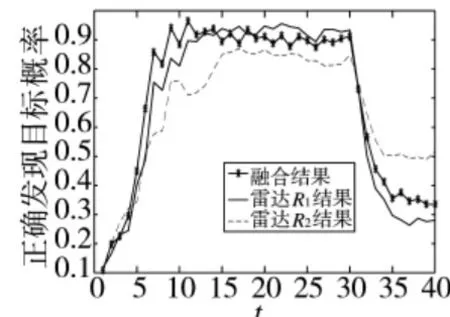
图11 信噪比12的目标正确发现概率

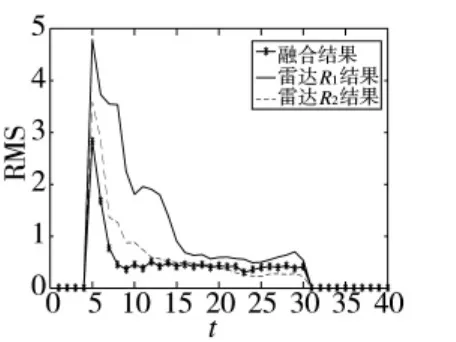
图12 信噪比12的目标位置估计RMS比较结果

由图9可见，当目标做匀加速直线运动时，在第5 s～11 s阶段，利用本文算法对两部雷达的量测信息进行融合后，与单雷达相比，融合后得到的目标的正确发现概率仍有明显提高。在第7 s时，融合后对目标正确发现概率达到0.88，而此时，雷达1的目标正确发现概率仅为0.57，雷达2的目标正确发现概率为0.49。在第9 s时融合后得到的目标正确发现概率高达0.93，之后稳定在0.87附近。由图可见，本算法对目标正确发现概率有着明显的提高。

由图10可见，利用本文算法对两部雷达的量测信息进行融合后，与单雷达的检测跟踪结果相比，目标跟踪精度得到明显改善。在第5 s目标出现时，跟雷达1相比，本文算法的误差降低了12%，与雷达2比较，降低了20%。之后融合后的误差急剧减小，在第9 s时效果明显，与雷达1相比，误差降低24%，与雷达2相比，误差降低37%。当跟踪稳定后，融合后的误差稳定在6%左右，与雷达1和雷达2的误差相差不大。

图7、图8分别为信噪比为 5，即 P=1.5、Q=0.3情况下的目标正确发现概率图和RMS比较图。图11、图12为信噪比为12，即P=3.6、Q=0.3情况下的目标正确发现概率图和RMS比较图。由图可知，本文算法在目标做匀加速直线运动时仍可以有效地降低误差和提高目标正确发现概率。