附加先验概率条件下的最佳先验概率选取
2019-06-15王平波卫红凯
代 振,王平波,卫红凯
(海军工程大学电子工程学院,武汉 430033)
0 引言
贝叶斯准则是进行假设检验的通用准则,在代价因子和先验概率已知的情况下,基于贝叶斯准则确定检测门限可以使判决付出的平均代价最小[1-3]。当先验概率未知时,不能直接使用贝叶斯准则进行判决,此时通常采用贝叶斯准则的派生准则-极大极小准则。极大极小准则是在所有可能的先验概率中选择最不利的先验概率来确定检测门限,其判决代价与真实先验概率无关,从而避免了由于先验概率未知可能导致的极大的判决代价[4]。但是,当真实的先验概率与最不利先验概率相差较大时,采用极大极小准则的判决代价远大于贝叶斯准则下的判决代价。实际情况中,即使无法确定真实的先验概率,但是可以根据一定条件大致估计出先验概率的区间范围。例如,在雷达观测中,敌机出现或不出现的先验概率是很难确定的,但是可以根据雷达的工作环境,从统计的方法给出敌机出现的先验概率区间[5],称之为附加先验概率条件。
本文对附加先验概率条件下的二元假设检验问题进行研究,提出了在不同先验概率条件下最佳先验概率的选择方法。根据最佳先验概率确定检测门限,可以有效降低判决代价。
1 贝叶斯准则下的二元假设检验
对二元假设Hj(j=0,1)进行检验时,判决代价为
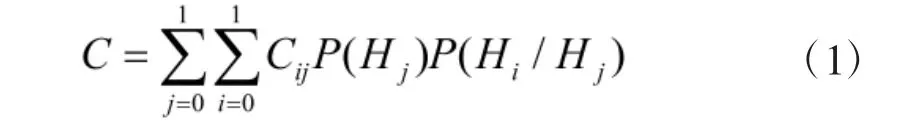
式中,P(Hj)表示Hj出现的先验概率,P(Hi/Hj)、Cij分别为Hj为真时判决Hi成立的概率和代价因子。
记Hi的判决域为Ri(i=0,1),则
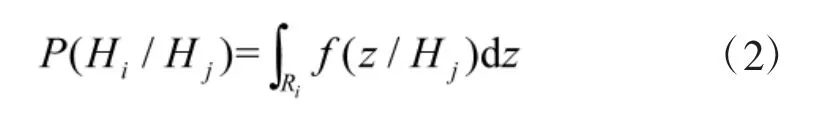
式中,f(z/Hj)为假设Hj(j=0,1)下的条件概率密度,又称似然函数。
当代价因子Cij已知时,对于给定的先验概率P(H1)=p1,采用贝叶斯准则划分判决域,可使判决代价最小。判别表达式为
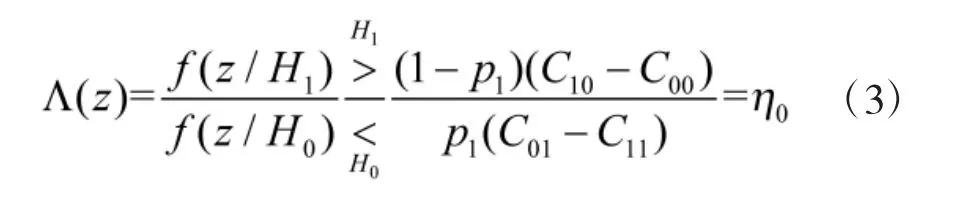
Λ(z)为似然比,η0为判决门限,当似然比大于门限时判H1成立,否则判H0成立。
记对应于先验概率p1的最小判决代价为Cmin(p1),因为P(H0)=1-p1,又P(H1/H0)=PF,P(H0/H1)=PM,P(H0/H0)=1-PF,P(H1/H1)=1-PM,带入式(1),可得
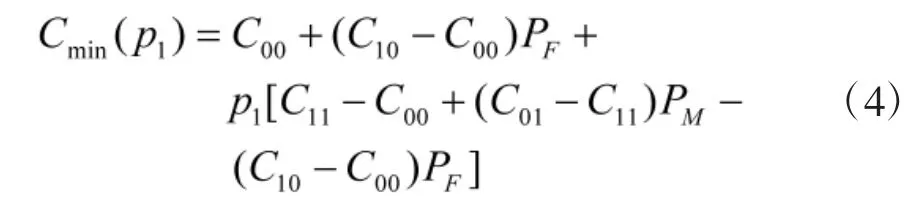
式中,PF和PM均是p1的函数,表达式如下
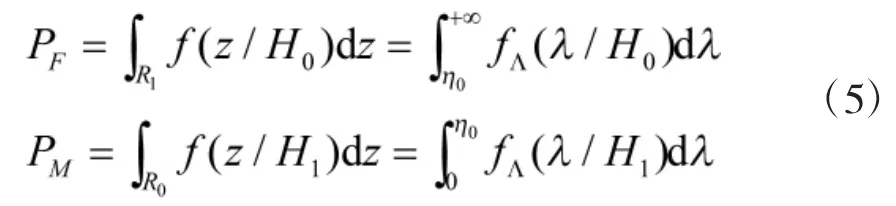
2 最佳先验概率选取
如果代价因子Cij已知,并假设先验概率,由于p1未知,不能直接利用贝叶斯准则进行判决。此时可以假定一个先验概率,并用其计算检测门限,将判决代价记为 C(p1g,p1),其表达式如下
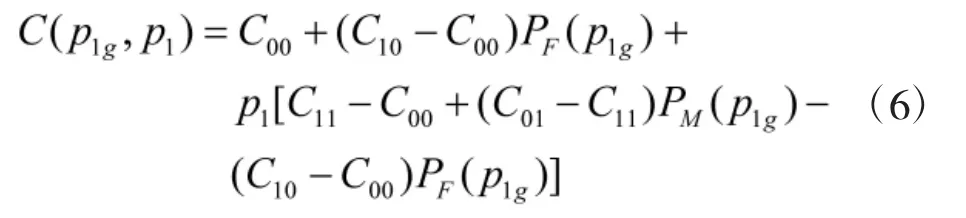
显然 C(p1g,p1)与 p1是线性关系,且 C(p1g,p1)≥Cmin(p1),当且仅当p1g=p1时取等号。又Cmin(p1)是先验概率p1的上凸函数[6],所以C(p1g,p1)与Cmin(p1)在点p1g处相切,如图1所示。从图1可以看出,p1g与真实的先验概率P1相差越大,C(p1g,p1)与Cmin(p1)相差就越大(如点p1b处)。因此,希望找到一个最佳先验概率p0∈[p1a,p1b],使得C(p0,p1)逼近Cmin(p1)。

图1 判决代价随先验概率P1变化的曲线
2.1 极大极小准则下的最佳先验概率
极大极小准则是指在先验概率区间[p1a,p1b]内,选取最佳先验概率p0,使得最大判决代价Cmax(p0)取得最小,其表达式如下
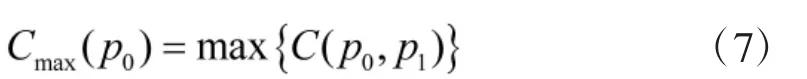
记Cmin(p1)取最大值Cminmax时的先验概率为p1*,显然,C(p1*,p1)是一条平行于 x 轴的直线,如图2所示。此时,C(p1*,p1)恒等于 Cminmax,与先验概率无关,可以保证最大判决代价最小,故p1*就是极大极小准则下的最佳先验概率。为求出 p1*,令 C(p0,p1)的斜率为零,即
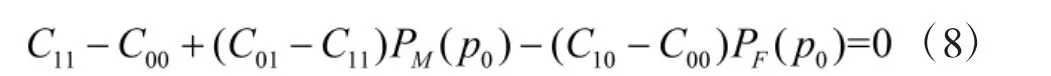
由式(8)即可解得 p1*,式(8)又称为极大极小方程。
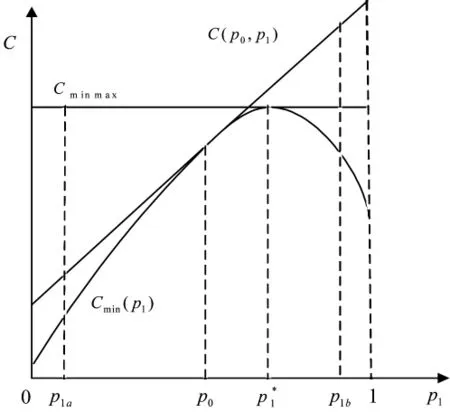
图2 判决代价随最佳先验概率p1变化的曲线
2.2 最小二乘意义下的最佳先验概率
极大极小准则虽然可以使极大判决代价极小化,但是当真实的先验概率p1与p1*相差较大时(如图2点p1a处),Cminmax会远大于Cmin(p1)。为解决这个问题,可以采用最小二乘法。最小二乘是指在先验概率区间[p1a,p1b]内,选取最佳先验概率 p0,使得e(p0)最小,其表达式如下
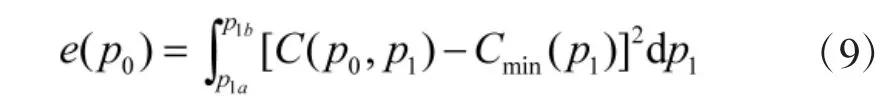
3 算例仿真
以高斯白噪声中恒定电平检测问题为例进行仿真分析。设有两种假设

式中,vi是均值为零,方差为a的高斯白噪声序列,N表示观察次数,A为大于零的常数。
不同假设下的似然函数分别为:
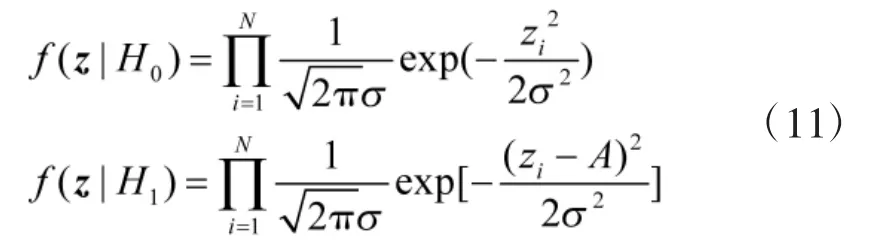
假设先验概率为 p1,令 C00=C11=0,C01=2,C10=1,则贝叶斯判决表达式为
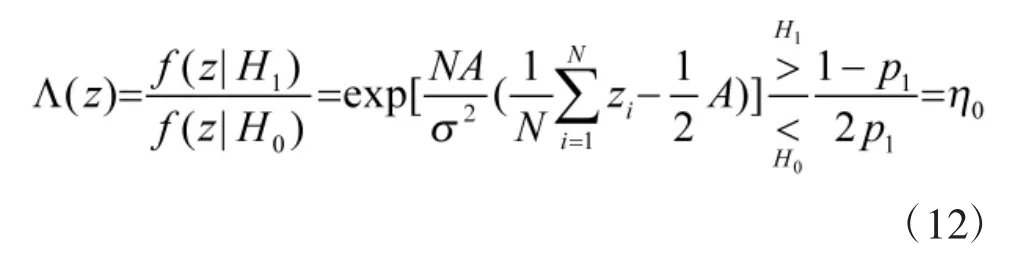
化简可得
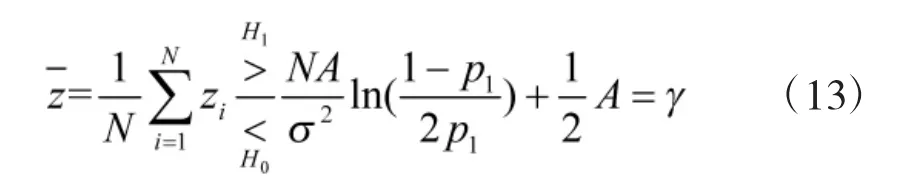
将式(13)带入式(4)、式(5)可得
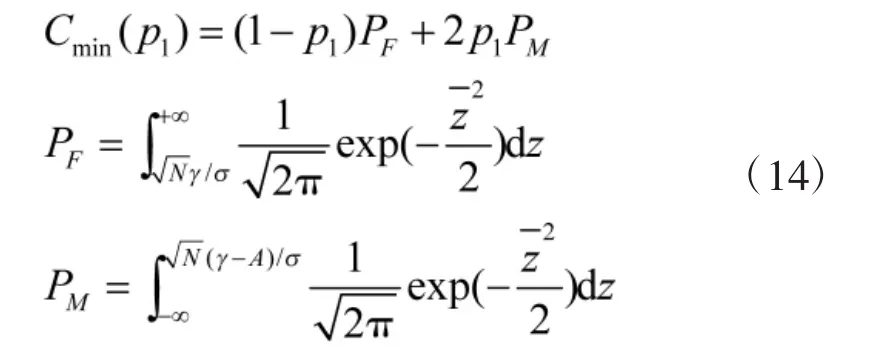
根据极大极小方程,可得

由式(15)解得p1*后,不妨取,并记可以看作信噪比。此时,极大极小准则下的最佳先验概率为p1*,最小二乘意义下的最佳先验概率为p1*/2,分别取最佳先验概率为p1*和p1*/2进行仿真,结果如图3、图4所示。
从图3(a)可以看出,不同信噪比下的判决代价误差 e(p1*/2)始终小于 e(p1*),并且当信噪比 d<1时,e(p1*/2)远小于 e(p1*)。此外,e(p1*/2)始终接近于零,表明C(pp1*/2,p1)对Cmi(np1)的逼近程度较高。从图3(b)可以看出,不同信噪比下的最大判决代价Cmin(p1*)始终比Cmax(p1*/2)小,符合极大极小准则的判断,但是二者差距并不突出,这说明当时,最佳先验概率应该选择p1*/2。
图4进一步给出了d=0.3以及d=1时的判决代价曲线。从图4可以直观地看出,Cminmax与先验概率无关,但在较低的先验概率处,其值远大于Cmi(np1)。而则与Cmi(np1)较为接近,尤其是在信噪比较低时,与Cm(inp1)基本重合。
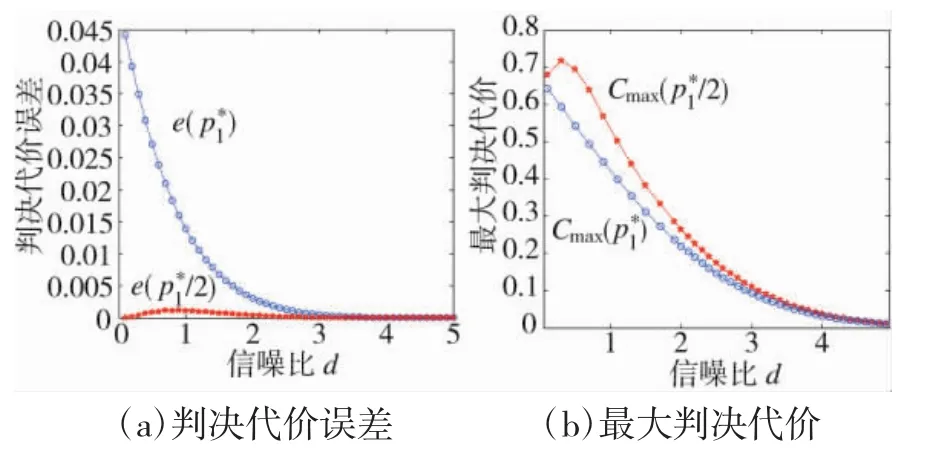
图3 不同信噪比下的判决代价误差与最大判决代价,p1∈[0,p1*)

图4 不同信噪比下判决代价曲线,p1∈[0,p1*)
4 结论
对二元假设检验问题进行了研究,在附加先验概率条件下,提出了最小二乘意义下的最佳先验概率,将其与基于极大极小准则确定的最佳先验概率进行综合比较,给出了任意附加先验概率条件下的最佳先验概率选择方法。仿真结果表明,根据最佳先验概率确定检测门限,在先验概率未知时可以有效降低判决代价。
