协同条件下的空空导弹作战效能分析*

王 磊，程相东，彭建亮

（空军西安飞行学院，西安 710306）

0 引言

随着航空武器作战平台和信息技术的发展，三代机逐渐成为部队的主战装备并已经开始向四代机发展，以协同为基础的体系作战业已成为航空作战平台最主要的作战手段。空空导弹武器系统作为航空作战平台间对抗的主要武器，其作战效能的有效发挥将直接影响空战态势，这也使其成为航空武器平台协同作战的主要研究对象。传统的作战效能评估［1-3］，忽略了信息系统的支持，未充分考虑航空武器平台间协同对空战的巨大影响，评估结果已经不能真实反映信息化战场协同条件下的武器作战效能，甚至与实际情况相悖。对协同条件下的空空导弹武器系统进行科学合理的评估，不仅是空战态势、战术效果分析的现实需求，也是指挥和作战人员进行战场分析、组织筹划、战术协同等战场行为的主要依据。

1 空空导弹综合评估体系分析

针对现有评估方法存在的问题，根据信息系统支持下的空空导弹协同主要提升信息和认知领域指标的特点，本文结合作用域（OD）理论［4］和ADC模型［5］计算过程，建立如图1所示空空导弹综合评估法流程：首先，确定各级能力指标和基层指标作用域，并对基层指标进行作用域划分；其次，根据不同的应用和评估需求确定各作用域的权重，计算各级权值，并进行一致性分析；再次，对基层能力指标进行分析并建立评估模型，计算指标值；最后，各基层指标的等级区间，结合指标值确定属性优劣等级和重要性等级，代入各自权值计算能力指标C。

图1 基于OD的综合评估流程

完成了评估方法设计后，需要结合评估方法设计相应的评估体系。显然协同作战同时发生在信息域Din、认知域Dco和物理域Dph；在物理域，表现为对空中、地面目标的杀伤；在信息域，表现为空战双方对对方信息的争夺与控制；在认知域，是对作战人员能力素质的全面考验。

根据图1所述综合评估法，对空空导弹综合评估体系的研究首先结合相关文献［6-7］建立作战能力的指标体系，并对其基层指标按照物理、信息、认知的作用域进行划分，其关系及代码可描述如图2所示。通过分析可见，空空导弹武器系统的次级指标中仅机动毁伤能力Cde全部由物理域指标构成，其指标能力不受数据链的影响，是导弹武器固有的能力，其余的次级指标在加装了数据链系统后都有了不同程度的影响：

1）空空导弹武器在协同条件下，需要综合考虑载机编队中友机的探测能力，在战场条件下还需要综合考虑预警机、地面雷达等作战平台的探测能力。

2）协同条件下的空空导弹武器系统通过数据链系统连成了一个整体，导弹发射能力已从单一的允许发射区扩展为协同发射区。

3）编队飞机完成目标分配，发射空空导弹后，载机需要通过武器协同数据链对已发射的导弹进行弹道修正，协同条件下在载机受到威胁时，转换制导载机继续进行制导。

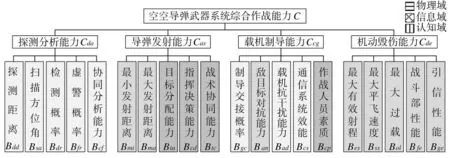
图2 基于作用域的空空导弹武器综合评估指标体系

2 基于OD的评估指标权重逆向分析

一般情况下，分析能力指标C时，首先从根指标开始，直至其基层指标。而在将作用域理论引入评估体系后，如果继续采用这种自上而下的权重分析方法，就无法有效体现协同条件对空空导弹系统的影响。所以在权重计算过程中应首先考虑作用域的因素。

2.1 作用域指标排序

各武器系统由于担负的职能不同，在作战使用中对预警通信、指挥控制、作战毁伤的侧重也有所不同，武器系统的预警通信过程较为关注系统的Din指标，指挥控制过程更关注系统的Dco指标，作战毁伤过程则主要依赖系统的Dph指标。因此，在空空导弹作用域指标权重排序时需要综合考虑不同作战平台的作战使用特点，具体计算过程如下：

以整个作战过程P为准则，所支配的子作战过程为预警通信ps、指挥控制pc、作战毁伤pd，根据不同的武器系统作战过程的侧重，将其子作战过程的重要性分别记为ws、wc、wd，并根据公式建立判断矩阵EP。

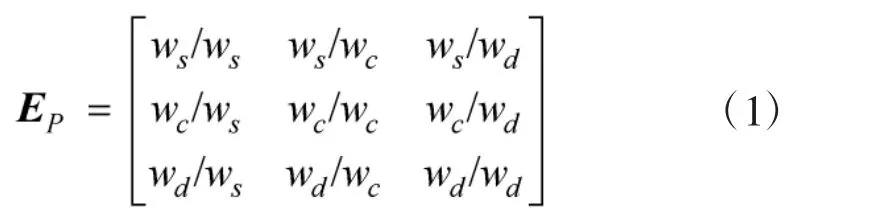
计算判断矩阵每行所有元素的几何平均值

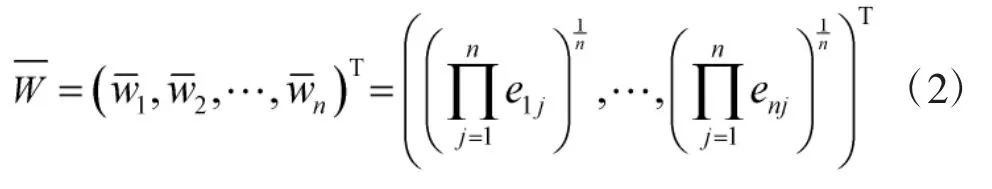
归一化，求得特征向量的近似值，即各作用域的相对权值向量：

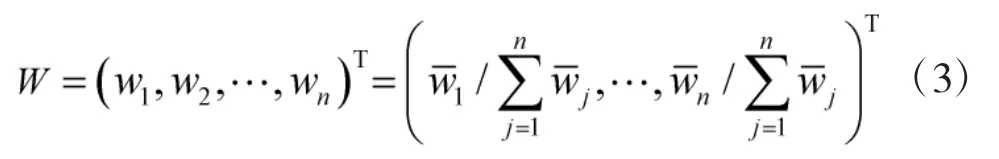
同理以作用域D为准则，按照预警通信的需求将其包含的信息域Din、认知域Dco和物理域Dph元素的重要性分别记为 wsi、wsc、wsp，建立判断矩阵 Es：

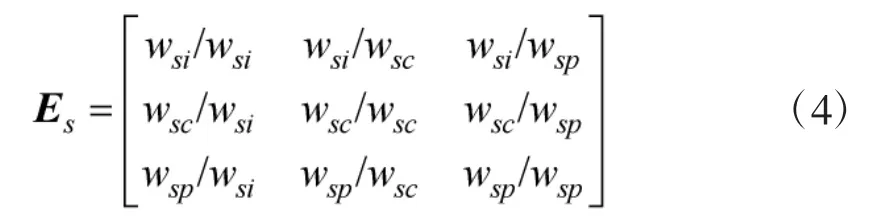
并根据式（2）～式（3）计算各作用域在预警通信过程中的相对权重 Ws=（wsin，wsco，wsph）。

同样方式以作用域D为准则，按照指挥控制和作战毁伤的需求建立其判断矩阵Ec、Ed，并分别计算其权 重向量 Wc=（wcin，wcco，wcph）、Wd=（wdin，wdco，wdph）。

而后按照式（5）综合作用域在整个作战过程中的权重向量 WD=（wDin，wDco，wDph）：

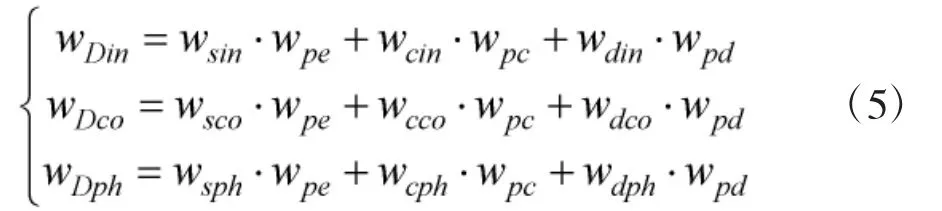
2.2 各级指标排序

同样方法根据各作用域相关指标构造基层指标关于各作用域的判断矩阵，计算基层指标相对所属作用域的权值向量 WIn、WCo、WPh，在得出基层指标关于各作用域的相对权值后，根据式（6）计算基层指标绝对权值W：

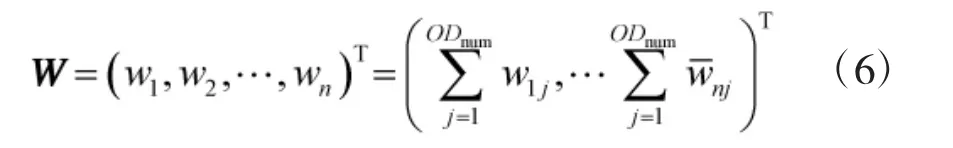
式中，ODmum为作用域数目，n为基层指标的数量，wn为第n个基层指标的权值，其值为指标n在各个作用域的相对权值之和，而wij的计算公式为：

wDj为WD中第j个作用域的权值，wj（i）为第i个指标相对于第作用域j的权重。

排序完成后根据式（8）计算总排序一致性指标和随机一致性指标：

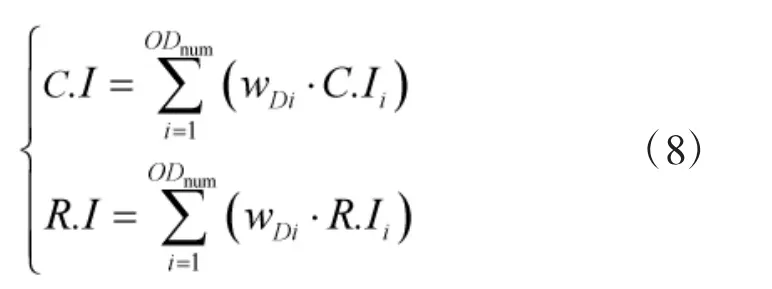
而后根据式（9）计算次级能力指标权值向量Whp：

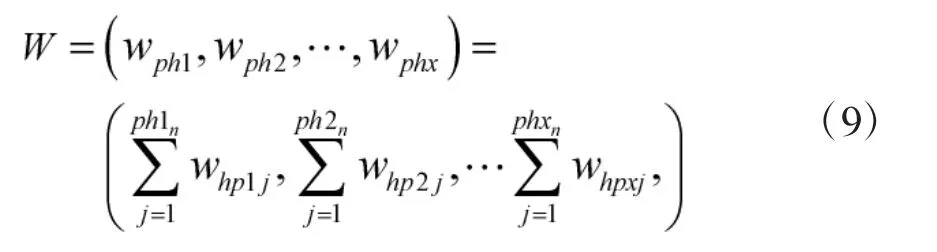
whpx为第x项次级指标的权值，hpxn为与第x项次级指标相关的基层指标数。

3 基于模糊理论的灰色评估策略

3.1 标准AHP灰色评估法

基于AHP的灰色评估法［8-9］是以灰色理论为基础，以AHP、ADC效能评估模型为指导的定性指标量化分析方法。具体步骤可描述如下。

1）建立评价样本矩阵。邀请相关领域的p位专家依据评分等级对各指标进行打分，确定其评价样本矩阵Q：

其中，m为一级指标数，n为评价等级，ni为一级指标i下的二级指标数，qinjk为第k位专家对一级指标i的第j个指标的评价值；

2）建立灰色评价矩阵。首先确定评价灰类的等级数、灰类以及灰数的白化权函数 fe（qijk）（k=1，2，…，p；e=1，2，…，g），而后根据式（11）～ 式（13）分别计算第e个评价灰类的灰色评价系数xije，各评价灰类的总灰色评价系数xij，第e个灰类的灰色评价权rije：

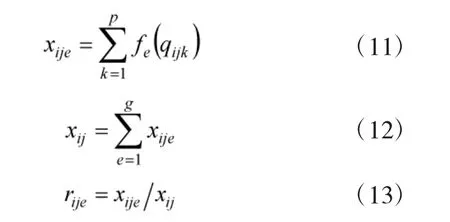
可得评价指标Vij的各个灰类总评价向量

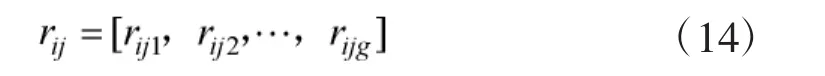
对Vi所属指标的各评价灰类的灰色评价向量综合后，建立其灰色评价矩阵：

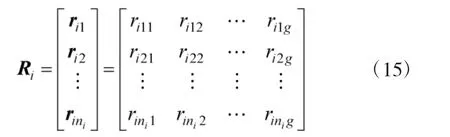
3）对指标进行灰色综合评价。

首先，对Vi作一级综合评价，其结果记为Bi，其中Ai表示Vi中各因素的权重：

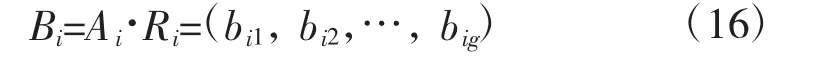
其次，由 Bi得到总灰色评价权矩阵 R=（B1，B2，…，Bm）T，则二级综合评价结果 B：

其中，A表示V的各因素的权重。

最后，计算综合评价值，对各灰类按“灰水平”赋值，得各评价灰类的等级值化向量C=（c1，c2，…，cg），于是综合评价值W：

3.2 模糊理论的引入及改进

基于OD的空空导弹评估指标体系中物理域、信息域指标多是定量指标，认知域指标多是定性指标，采用灰色评估法只能牺牲定量指标的精确性，这样过度放大了人为因素对系统最终效能的影响。要提高现有评估法的准确性和可信性，将模糊理论［11-12］引入灰色评估法，对其进行改进。具体过程可描述如下：

1）根据属性等级设定模糊数 S=［s1，…，sm］T和权向量 W=［w1，…，wm］T的模糊区间，通过判断精确基层指标所属等级，形成对次级或更高级指标的精确评价。

2）采用式（19）～ 式（20）为次级能力指标建立加权规范化决策矩阵D：

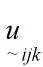
3）在建立所有次级指标的决策矩阵后，分别确定其基层指标的正理想指标和负理想指标向量：

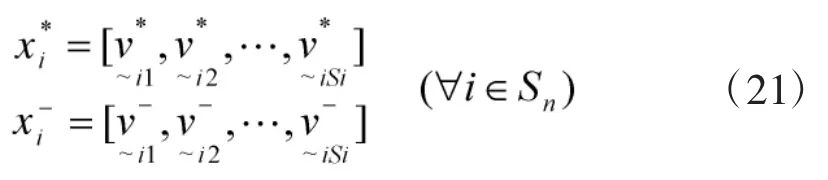
在对模糊数进行排序时可采用概率分布法，可将参与比较的模糊数看成一随机变量，概率密度函数为，然后利用模糊事件的概率测度特征量即均值和方差作为比较的准则：如果，则；如果，则。

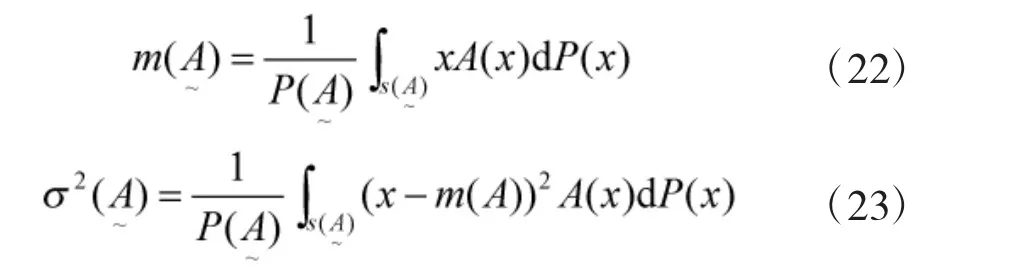
4）采用扎德贴近度刻画每个次级指标Ci的第k个相关基层指标的第j个评价到正理想指标和负理想指标的距离：

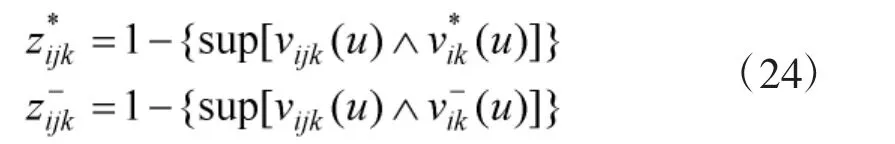
5）计算每个专家对次级指标i评价到正理想解和负理想解的距离：

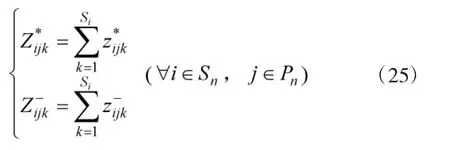
6）计算次级指标i的第j个专家评价与理想指标的相对接近指数矩阵Cij：

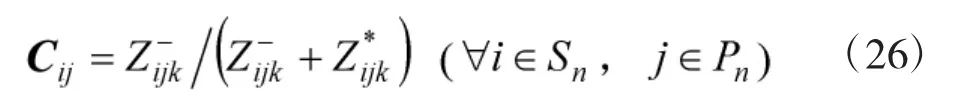
得出第 i个指标的评价样本向量 Ci=［Ci1，Ci2，…，CiPn］T。而后综合所有次级指标评价样本向量生成评价样本矩阵 C=［C1，C2，…，CPn］，采用灰色分析法计算系统综合能力效能。

4 实例分析

4.1 作用域指标排序

以空中双机编队对抗为背景，分析其协同条件下的空空导弹武器作战效能。以整个作战过程P为准则，所支配的子作战过程为预警通信ps、指挥控制pc、作战毁伤pd，根据不同的武器系统作战过程的侧重，将其子作战过程的重要性分别记为 ws、wc、wd，并根据式（1）建立判断矩阵 EP，并采用式（2）、式（3）计算其权重向量：

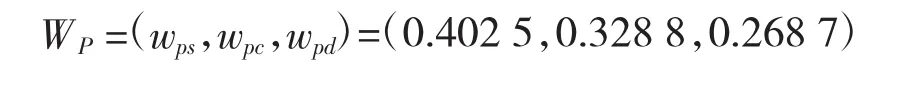
同理以作用域D为准则，按照预警通信、指挥控制和作战毁伤的需求，建立判断矩阵Es、Ec和Ed，并分别计算其权重向量 Ws、Wc、Wd。最后按照式（5）综合作用域在整个作战过程中的权重向量WD：

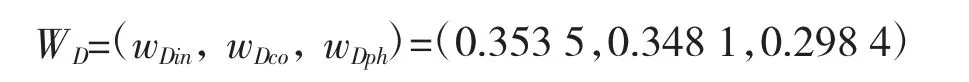
4.2 各级指标排序

对各作用域建立各自相关基层指标的判断矩阵Eph、Ein、Eco，并分别计算各自基层指标的相对权值 Wph、Win、Wco。而后，如表1所示，在计算基层指标关于各作用域的相对权值后，计算AAMSDL基层指标绝对权值W和级次指标相对权值WC，并按照式（8）进行一致性检验：

表1 基层指标绝对权值

根据式（8）计算总排序一致性指标和随机一致性指标：C.I=0.003 7，R.I=0.871 3。则层次总排序随机一致性比率：C.R=C.I/R.I=0.004 2＜0.10，指标排序的计算结果具有满意的一致性，指标权重可以接受。

4.3 综合效能评估

由于本文主要研究其评估体系，就不介绍如何获取基层指标样本值，现直接给定某导弹系统、载机和相关人为要素指标值，如表2所示。

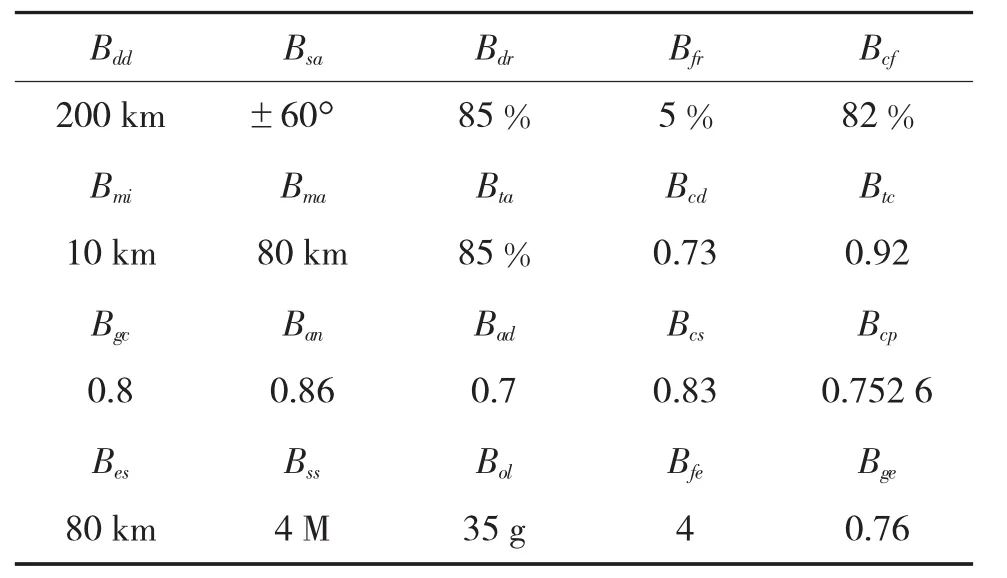
表2 某空空导弹系统基层指标值

根据实际问题，采用表3所示模糊数将指标属性优劣和相关指标间重要性分为4个等级。

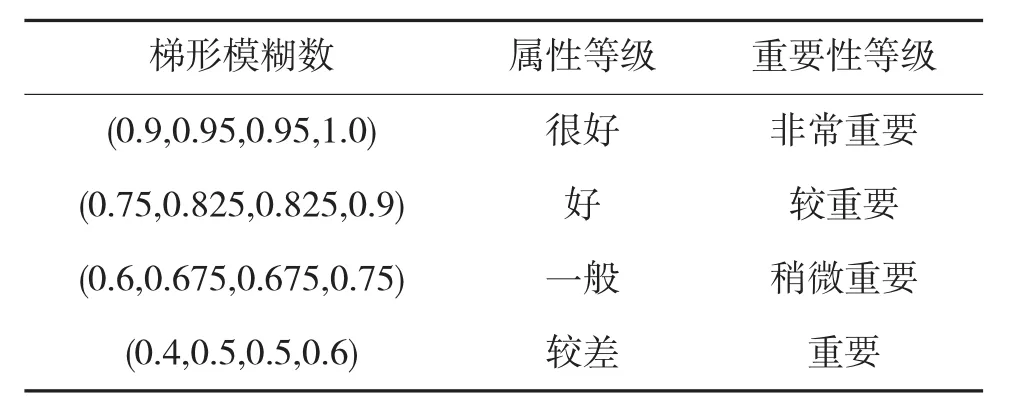
表3 优劣等级和重要性等级对应梯形模糊数

通过领域专家对图2所示基层指标划定等级，确定不同等级条件下的精确效能，并代入式（19）～式（26）计算各次级指标评价样本向量，得出综合评价样本矩阵C。而后按式（11）计算各能力所有指标评价灰类的灰色评价系数，代入式（12）计算灰类的总评价系数分别为 x1=12.190 1、x2=12.045 6、x3=11.818 2、x4=13.085 6。通过式（13）获得评估灰类的灰色评估矩阵后，代入式（17）得到系统关于各灰度的综合指标评价向量，并通过式（18）最终获得导弹武器系统在协同条件下能力指标效能的综合评估值：C=0.903 7；同理计算其在不协同条件下的综合评估值得C=0.564 8。