基于Cholesky分解的自适应抗干扰算法

齐志强

（中国空空导弹研究院，河南 洛阳 471009）

0 引言

卫星导航定位系统目前已广泛应用于精确制导武器系统和其他需要导航定位的平台上，如飞机、船舶、车辆等。卫星导航定位系统采用扩频技术，到达地面的信号强度比白噪声低20 dB左右，工作频率固定，很容易遭到敌方的压制干扰而导致无法正常工作［1］，因此，抗干扰能力成了制约卫星导航定位系统应用的瓶颈［2］。为了满足在复杂电磁环境下的应用需求，军用卫星导航定位产品多采用阵列处理天线来提高抗干扰能力［3］。

目前采用阵列信号处理来进行卫星定位系统的抗干扰处理算法主要有两大类:一类是闭环算法，另一类是开环算法。常用的闭环算法以LMS算法为典型代表，该算法实现简单，计算量小，因而成为美军早期采用的主要的抗干扰算法。但该算法的收敛速度与其输出协方差矩阵的特征值分布相关，其收敛速度随着干扰信号强度和干扰信号的类型变化而变化，当特征值散布较大时，收敛速度慢［4］，特别是在动态载体上难以收敛到最优值。开环算法的收敛速度快，被认为是实现自适应抗干扰处理的最优算法［5］，已成为国内外研究的热点方向。开环算法主要有多级维纳滤波MSNWF（Multistage Nested Wiener Filter）和 SMI（Sample Matrix Inversion）算法［6-7］，MSNWF算法虽然具有良好的降秩性能，但降秩处理会影响阵列自由度，使干扰抑制性能下降［8］，而且MSNWF算法包含前向迭代和后向迭代，当振元数目过多时，计算量迅速增加，难以满足实时性的要求［9］。传统的SMI算法需要进行矩阵求逆运算，硬件系统复杂［10］，实现困难［11］，为解决此问题，通常用矩阵分解的方式来实现。本文主要阐述基于Cholesky分解的自适应抗干扰算法应用研究。

1 自适应抗干扰算法

卫星导航定位系统由于接收到的信号比较弱，湮没在白噪声中，而干扰信号比较强，常用的抗干扰算法主要有自适应调零和自适应波束形成技术，自适应波束形成技术被认为是干扰抑制最有效的工具之一［12］。文献［12］推导的自适应波束形成算法最终需要求得的权值表达式为:

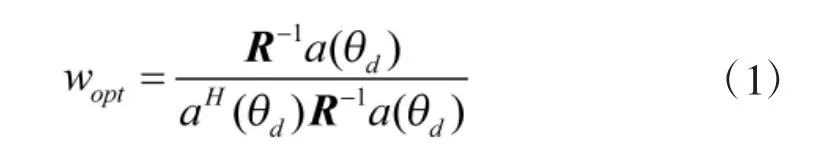
式（1）中，a（θd）为阵列在 θd方向的阵列响应，R 为输入信号的协方差矩阵，a（θd）和 R 的求解在文献［12］中已有详细的推导，这里不再重复。从式（1）中易见，权值求解的关键在于求得协方差矩阵R的逆矩阵。

2 矩阵求逆的方法

自适应抗干扰算法的主要运算，最终归结为对输入信号的协方差矩阵求逆问题。矩阵求逆的方法较多，而矩阵求逆方法的选择不仅关系硬件资源的占用量，还关系着权值的更新速度。因此，对于硬件平台来说，由于硬件资源有限，需要找到一种既耗费资源少，又可以快速完成矩阵求逆的方法。

矩阵求逆最基本的方法是Gauss消元法，但该方法计算步骤繁多，运算量大，不适合硬件实现。硬件实现时通常采用矩阵分解的方法，将矩阵转换为特殊矩阵，从而简化运算。矩阵分解常用的方法有LU 分解［13］，QR 分解，Cholesky分解等方法，LU 分解结果不唯一；QR分解需要将矩阵分解为一个正交矩阵和一个上三角矩阵，并且需要求平方和开根号，步骤繁多，利用硬件实现比较困难［14］；Cholesky分解需要用到开方和除法，不太适合FPGA实现，但近年来随着FPGA的规模越来越大，用FPGA来完成Cholesky变换，资源问题已不再成为问题的瓶颈［15-16］，因此，本文拟采用Cholesky分解来实现权值求解。

3 Cholesky分解求权值方法

R是秩为n的赫米特矩阵，利用Cholesky分解可求得下三角矩阵G，使R=GGH。

矩阵R可以写作如下形式:

则存在下三角矩阵:

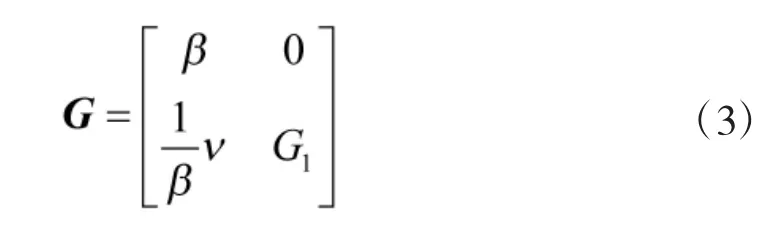
由式（3）可知，要得到矩阵G，需要分3步走:

第3步:求解矩阵G1。令，则有，G1为下三角矩阵，显然，矩阵G1的求解过程和矩阵G的求解过程相同，先算出矩阵R1，然后采用相同的方法即可逐步求出矩阵G1中的全部元素。

将式（4）两边同乘以 R，并将R=GGH带入，可得:

式（5）中 a（θd）为 n×1 的列向量，G 为 n×n 的下三角矩阵，令，则T为n×1的列向量，式（5）可以写为:

式（6）可以用Gauss消元法求得T，以n=4为例，式（6）可以写为:

由式（7）可求得 T，

4 FPGA实现

用FPGA实现Cholesky分解求权值，需要3个功能模块，如图1所示:

图1 Cholesky分解求权值模块结构图

控制模块负责协方差矩阵R和导向矢量a（θd）的调取，协调Cholesky分解模块和Gauss消元模块的数据进出及时序控制，并将最终求得的权值输出。

Cholesky分解模块完成对协方差矩阵R的分解，求出下三角矩阵G。由上面的介绍可知，Cholesky分解由3个计算单元组成:第1个计算单元进行开方运算，求出矩阵G的第1个元素，；第 2个计算单元求出矩阵G的第1列其他元素，；第3个计算单元更新下三角矩阵中的其他元素，即求出。由于下三角矩阵G1为n-1维矩阵，因此，上述3个计算单元可在控制模块作用下重复利用，最终完成下三角矩阵G的求解。

Gauss消元模块只需要一个计算模块即可完成两次Gauss消元的全部运算，以4振元为例，只需完成计算模块，当计算t1时，控制模块将a1赋给a4，将G11赋给G44，其他元素赋0即可，在控制模块作用下，依次算出 t1，t2，…，t4。

上述计算过程多是顺序执行，需要几百个时钟周期才可以完成一次权值更新，但协方差矩阵也是需要多个时钟周期的样本数据才可求得［12］，即使1 000个时钟周期更新一次权值，以系统时钟62 MHz为例，更新周期也只有16 μs，足以满足高动态条件下的权值更新要求。

表1列出了几种常用自适应抗干扰算法的比较情况，其中M代表阵列的维数，D表示MSNWF降秩后的维数。

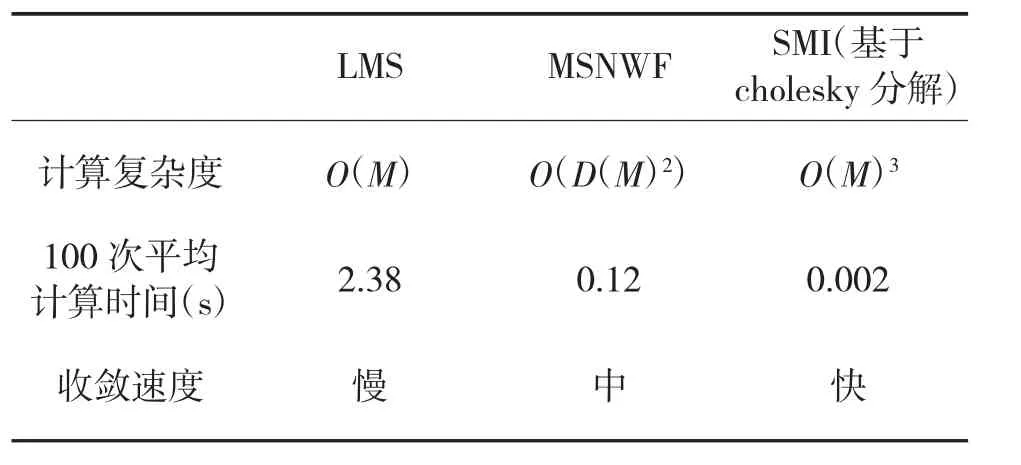
表1 几种常用自适应抗干扰算法的比较

从表1可以看出，SMI算法性能最优，但计算复杂度也最高，因为该算法需要开方和除法运算，这也是很多人望而却步的原因。本文所述方法由于可以实现资源复用，仅需要1个开方模块和1个除法模块，乘法器也可以复用，cholesky分解所需乘法器数量仅和LMS算法相当，因此，该算法对资源的需求并不是特别大，完全可以用FPGA来实现。

5 结论

本文所述的基于Cholesky分解的自适应抗干扰算法巧妙地回避了矩阵求逆运算，大幅度降低了运算复杂度，扫除了利用FPGA实现的障碍。按照文献［12］所述方法，已在工程上实现，其抗干扰效果可达80 dB以上，特别是在高动态载体上，依然可以获得优异的抗干扰性能。该方法不但可以应用于空域抗干扰技术，也适用于空时抗干扰算法，应用前景广泛。当载体姿态不易获知时，可以将导向矢量a（θd）设为固定值，以4振元为例，当时为常用的功率倒置算法［17］，时则为Capon空域自适应抗干扰方法，当时为空时联合抗干扰方法［18］。