基于改进人工鱼群算法的反TBM目标分配策略*

王 楠 ，戴江斌 ，韩 钧

（1.西安体育学院，西安 710068；2.空军工程大学，西安 710051）

0 引言

反TBM（Tactical Ballistic Missile）的目标分配，是为应对大规模TBM进攻，将来袭的TBM合理分配至防空反导拦截系统，以实现对要地区域的防护。反TBM目标分配问题模型的有效性，算法的时效性决定了整个防空反导作战的效能，是指挥决策的核心内容之一。

反TBM目标分配问题属于NP完全问题，随着战场环境的日益复杂，参战兵力兵器和来袭TBM目标的增大，使得时间和空间复杂度呈指数级增长，传统求解算法（如分支定界法、匈牙利法、整数规划法等）已很不适宜，目前主要利用智能优化算法进行求解，如遗传算法［1］、禁忌搜索算法［2］、粒子群算法［3］、蚁群算法［4］及模拟退火算法［5］等，虽发展显著，但也普遍存在着早熟停滞现象，易陷入局部最优，且收敛速度较慢，无法满足当前防空反导快速实时要求。本文在考虑拦截效益和时空等约束的基础上建立了反TBM目标分配模型，并设计了带交叉变异算子的模拟退火人工鱼群优化策略，提升模型求解的速度精度，有效提高防空反导作战效能。

1 反TBM目标分配模型

1.1 目标函数

考虑反TBM目标分配拦截效益最大化，拦截TBM数量最大化，以及导弹消耗最小化的目标，建立目标函数模型为:

其中，F为拦截目标的效益；pij为武器i对弹道导弹目标j的拦截摧毁概率；wj为目标j的威胁值；x=［xij］n×m为决策变量集合。Y 表示拦截目标数；yj=1，表示目标j受到武器的拦截，yj=0，表示目标j未受到武器的拦截。R为武器总的拦截弹消耗数量。由于是多目标决策，采用线性加权法进行转换，将其转换为单目标最大化问题:

1.2 约束条件

1.2.1 空间约束

反TBM作战首先需要考虑拦截武器系统对来袭TBM在空间范围内是否构成拦截可能，因而建立空间约束条件为:

其中，Rij为目标j与武器i之间的直线距离，Rimax为武器i能拦截目标的最大远界；Vj为目标j的速度，Vimax为武器i能拦截目标的最大速度；Hj为目标j的高度，Himin和Himax分别为武器i能拦截目标的最小和最大高度。

1.2.2 时间约束

TBM飞行速度快，武器系统对其拦截时效性要求高，必须满足发射窗口的时间约束，且对应不同目标通道的武器系统，时间约束也不尽相同。

其中，tij为武器 i发射拦截弹时刻，tSij、tEij分别为目标j到达武器i发射窗口最早、最晚发射点时间。

同时，对于单目标通道武器系统，应满足:

对于多目标通道武器系统，应满足:

其中，N为目标通道数，Δti为武器i的射击周期，ΔtFi为多通道武器发射两枚导弹的时间间隔。

1.2.3 其他约束

本文对于其他约束条件，重点考虑上级的指令和同一TBM拦截次数。

对于上级指定拦截的目标，只要满足空间和时间约束条件，则至少保证有一个武器系统实施拦截，那么:

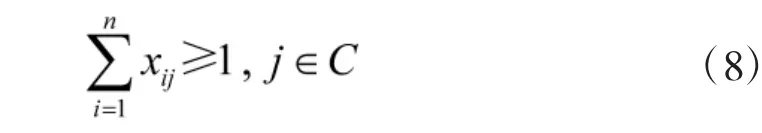
其中，C为上级或指挥员命令拦截的目标集合。

同时，对任一目标拦截的次数均不超过Num，即对任一目标拦截Num次，均能以较高的拦截效益值将其击毁，即

1.2.4 约束条件的处理

对于上述列举的约束条件，可以利用综合约束罚函数进行处理。对于式（4），若目标j相对武器i不满足约束，则武器i无法拦截目标j，则令pij=0。因此，仿真求解时可以不考虑此约束，认为pij=0即不满足此约束。

对于式（5）和式（6）决定的单目标通道武器时间约束，若需要拦截的目标数量是两个以上时，须判断是否存在发射的时间窗口，且先到先打，将武器i需要拦截的目标集合按到达武器i的发射区远界的先后顺序排列，设目标j最先到达发射区远界，则令tij=tSij，对第2个目标w的发射时刻，以此类推。综合约束罚函数为:

同理，对于式（5）和式（7）决定的多目标通道武器时间约束，设目标j最先到达发射区远界，则令tij=tSij，对第2个目标w的发射时刻，以此类推。综合约束罚函数为:

对于式（8），定义综合的约束罚函数，只要有一个子约束不满足，就可以知道解是不可行的，则综合约束罚函数为:

同理，对于式（9），综合约束罚函数为:

其中，M为惩罚因子，是一个很大的正数。至此，将带有约束的多目标决策问题转换成一个不带约束的单目标组合优化问题。

2 改进人工鱼群算法的目标分配方法

2.1 基本思路

人工鱼群算法是一种自下而上的新型寻优策略，但当部分人工鱼处于漫无目的的随机移动或人工鱼群在非全局极值点出现较严重聚集情况时，收敛速度大大减慢，同时，人工鱼群算法由于视野、步长的随机性和随机行为的存在，最优解的精度往往较低。

为有效应对以上不足，本文引入遗传算法中的交叉变异算子以提高收敛速度，通过设立公告板来记录最优人工鱼个体状态，人工鱼在行动一次后将当前状态的函数值与公告板进行比较，若优于公告板则用当前状态取代公告板状态，当最优个体状态在连续多个迭代过程中没有变化或变化极小时，开始交叉变异操作，保留历史最优人工鱼个体状态，将其他人工鱼按一定的概率对少部分维进行交叉变异，从而实现人工鱼的跳变，调整优化整个鱼群。并且同时引入模拟退火算法以提高收敛精度，对最优解状态的人工鱼个体进行局部模拟退火，“精细搜索”局部优化，提高整个算法的局部搜索能力。

具体本文的问题，人工鱼状态对应武器的目标分配即决策变量xij，人工鱼当前位置的食物浓度对应目标函数Z'。

2.2 算法流程

假设 n 个武器的编号为 1，2，3，…，n，m 个目标的编号为1，2，3，…，m。当第j个目标分给了第i个火力单元时，可令yj=i，则相应的分配方案（人工鱼状态）X 为:y1，y2，…，ym。这种编码方式直观、简单，并大大减少了个体总量和非可行的个体量。其反操作为:

用人工鱼所在位置的食物浓度表示目标函数Z'，即Y=Z'。人工鱼群通过觅食、聚群及追尾行为向食物浓度更大的区域游动的过程，就是动态寻优的过程，通过这一过程不断变化，使目标分配方案不断向最优解附近的区域靠近。具体算法流程为:

1）产生初始可行解:①对于第j个目标，将武器按射击的有利程度排队。若排在第k名的武器具备射击条件，则用F（j，k）表示该火力单元的代号，否则就置F（j，k）=0；②在可行域内构造L个个体如下:第 1 个个体 T1:F（1，1），F（2，1），…，F（M，1）；第h 个个体（h＜L）Th的构造为:假设 Th为:y1，y2，…，yM，对于 yk，若 F（k，h）≠0，则令 yk=F（k，h）；若 F（k，h）=0，则令 yk=F（k，1），其中 L 为群体规模；

2）公告板赋初值:计算初始鱼群各人工鱼个体当前状态的目标函数值Y，比较大小，取最大值者进入公告板，将此鱼赋值给公告板，并设置初始公告板最优人工鱼状态连续不变化或变化极小时的迭代次数Beststep为0，初始迭代次数Sum为0；

3）行为选择:各人工鱼分别模拟觅食、追尾、聚群和随机行为，选择行动后Y值较大的行为实际执行；

4）更新公告板:各人工鱼每行动一次后，检验自身的Y与公告板的Y，如果优于公告板，则以自身取代之；

5）变异条件判断:判断Beststep是否已达到预置的连续不变化次数的最大阈值，若是就执行第6步，否则转到第7步执行；

6）对鱼群内除公告板中最优个体之外其他所有人工鱼执行:①交叉操作:交换概率为pc，随机从人工鱼群中选择两个个体，执行单点交叉操作，然后将形成的两个新个体的函数值Y计算，并与公告板中的最优值进行比较，如果优于公告板，则以自身取代之；②变异操作:对各人工鱼的所有维分别产生随机数 r∈（0，1），如果 r＜pm，对该个体该维进行随机初始化，否则该维保持不变，对新形成的鱼群计算各人工鱼的函数值Y，并与公告板中的最优值进行比较，如果优于公告板，则以自身取代之；③置 Beststep为 0；

7）终止条件判断:判断Sum是否已达到预置的最大迭代次数或判断最优解是否达到了满意的误差界内，若不满足，则Sum=Sum+1，Beststep=Beststep+1，转到第3步执行，进行下一步鱼群优化过程，否则转到第8步执行；

8）对满意最优解域进行局部优化:调用模拟退火优化算法，对解进一步局部优化，产生高精度最终解；

9）如果结果满足约束则输出最优结果Y，即为分配问题目标值Z'，否则，增大罚函数值重新跳回第1步进行计算。

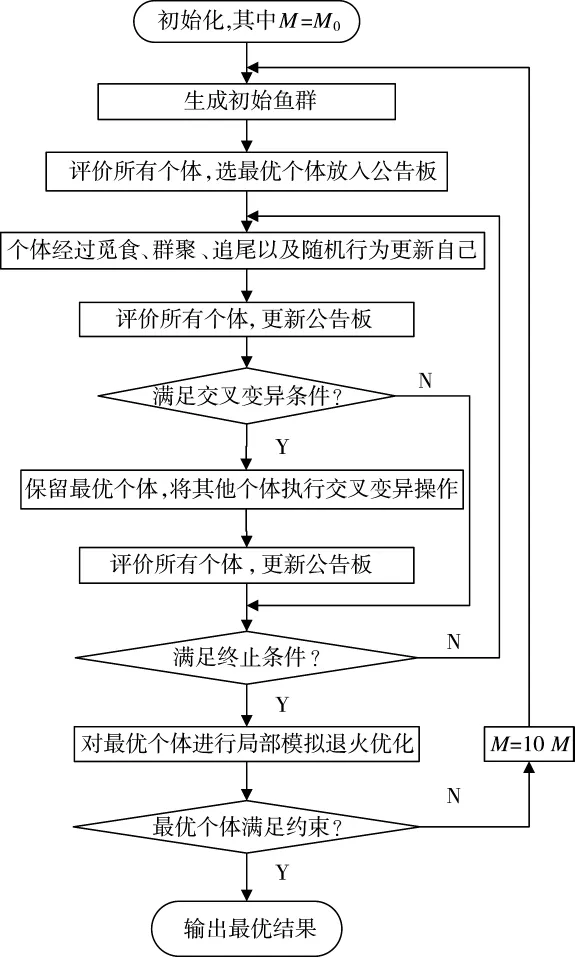
图1 算法流程图

3 算例分析

依据经验，对模型参数进行取值:最大拦截次数Num=5，子惩罚函数权重l=0.25（l=1，…，4），子目标函数权重 ωF=0.5、ωY=0.3、ωR=0.2，惩罚因子初值M=1 000；算法参数取值:人工鱼群规模Nf=300，可视距离Lvs=mn/20（表示人工鱼可视距离是解域的1/20），步长Lst=mn/40（表示人工鱼最大步长是解域的1/40），拥挤因子δ=0.11（表示90%的解域中只有不到10条人工鱼），交叉概率pc=0.5，变异概率pm=1/20 mn（表示一条人工鱼状态中只有一维改变的概率大概是0.05），模拟退火初始温度Ts=1，终止温度Tf=0.001，最大进化代数NSA=1 000。

武器系统数量n=6，其中单、多目标通道武器系统数量分别为4和2，来袭目标数量m=30，上级命令必须拦截的目标数为3（为一般化起见，随机选取）。目标到达武器系统拦截区远界的时间从［0，40］均匀分布随机选取，目标在武器系统的拦截区域停留时间从［25，50］中按均匀分布随机选取。目标威胁值从［0.2，0.8］中按均匀分布随机选取，拦截效益值在［0，1］中随机选取。武器系统的射击周期为20 s。多目标通道武器通道数为4，通道射击间隔为3.5 s。用设计算法求解10次后，结果按照目标函数值降序排列，如表1所示:

表1 目标分配结果

则对应最大Z'值的目标分配方案为:

将本文所设计的算法与粒子群算法（PSO）、蚁群算法（ACO）进行比较，分别随机运行50次，3种算法的性能比较指标如第73页图2所示。

从图2中可以看出本文所设计的算法在第10次迭代时便可以达到目标的最优分配，而PSO和ACO算法分别需要24次和36次迭代才能达到最优，且最优解及平均解均高于其他两种算法，说明本算法具有较好的收敛特性，能较快地找到问题的最优解，适应现代战争中反TBM作战辅助决策的要求。

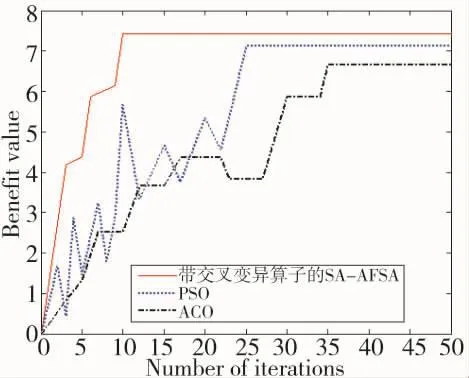
图2 算法性能比较图

4 结论

本文针对TBM饱和式攻击以及多弹头突防的战场环境，研究有效拦截时的目标分配问题。建立了体现多目标多约束决策模型，设计了带有交叉变异算子模拟退火人工鱼群复合算法，并进行了实验仿真验证，证明了算法的实时性和有效性。同时，对于作战想定、初始位和算法参数的确定还需要进一步探讨研究，以便更好地符合作战实际。