混合遗传算法的战时舰艇伴随保障人员优化配置*

2019-06-14张怀强卢远超

火力与指挥控制 2019年4期

张怀强，卢远超，王孟

（海军工程大学，武汉 430033）

0 引言

由于舰艇战斗载员等因素的限制，遂行一次作战任务的伴随保障人员总数往往是有限的，针对各舰艇进行科学的人员配置，以最大化地缩短战时累计修复时间，提升维修效率，对于保障舰艇作战能力意义重大。传统的人员配置方法如专家评估决策等，虽然一定程度上考虑了人员对装备的熟悉程度，但决策结果容易受伴随保障人员的职务级别及主观要求影响，难以有效保证战时维修效率最大化；同时人员配置方案随任务及人员数量的增加呈现级数增长，传统方法不易计算机实现，达不到战时快速制定最优方案的目标。因此，迫切需要探索一种有效缩短战时修复时间的舰艇伴随保障人员配置方法［1-4］。

本文以编队累计修复时间最短为目标，根据不同伴随保障人员对各舰载装备的维修效率及战时各舰艇装备体系的损伤概率，以核心装备最长修复时间控制为约束，分别计算不同伴随保障人员的组合配置方案下的各舰艇轻度故障的累计修复时间和重度故障的评估诊断时间，并利用混合遗传算法进行仿真，求解最优人员配置方案，有效提升了维修效率，缩短累计修复时间。

1 战时舰艇伴随保障人员配置分析

战时舰艇维修采取战场抢修的维修方式，包括战场损伤评估和战场损伤修复两部分内容。战场损伤评估是指从伴随保障人员获取装备战损信息、对战损装备进行损伤评估、确定战场维修资源和维修设施分布并进行现场维修或送修决策的全过程。战场损伤修复是指伴随保障人员根据前期损伤评估，对可以现场修复的轻度损伤进行维修并恢复其基本作战能力的过程［5-8］。

为了更好地解决问题，本文针对战时伴随保障人员配置作出如下假设:

1）由于作战载员数量有限，为保证舰艇综合战斗力，舰艇编队不可能配备大量的伴随保障人员，同时，作战任务的紧迫性也使得在短时间内难以动员到足够多的维修专家进行随舰保障。受此限制，战时舰艇伴随保障人员的总数是有限的。

2）在作战条件下，舰艇间的伴随保障人员换乘难度较大，人员流通性差，每位伴随保障人员只对所在舰艇实施单独维修保障，不负责其他舰艇的维修保障任务。

3）一艘舰艇可由一名或多名伴随保障人员负责保障，其组合效率与不同人员之间的默契程度有关。

4）各舰艇的战时累计修复时间，为各舰载装备在不同程度损伤下的战损评估时间和损伤修复时间之和。对于轻度损伤装备而言，由于其损伤信息获取与损伤评估的难度较小，战损评估时间远小于损伤修复时间，累计修复时间近似为损伤修复时间。对于重度损伤装备而言，由于损伤严重无法完成现场修复，伴随保障人员的主要工作为损伤评估与送修决策，因而其战时累计修复时间主要表现为战损评估时间。

5）舰艇核心装备的战损情况直接影响其他装备的功能发挥，因此，在不同的人员组合配置方案中，应优先保障核心装备的及时维修。

6）战时舰艇伴随保障人员组合配置的最优方案为一定约束下舰艇编队战时累计修复时间最短的方案。

2 配置方案模型的建立

2.1 单舰战时轻度损伤累计修复时间模型

根据假设可知，轻度损伤装备由于其损伤信息获取与损伤评估的难度较小，战损评估时间远小于损伤修复时间，可以忽略不计，其累计修复时间由损伤修复时间决定。

2.1.1 舰载装备轻度损伤预计维修工作量

舰载装备的数量、使用强度、装备损坏率、损坏程度比例等参数都与装备预计维修工作量有着密切关系。使用强度大，装备损坏率高，则维修工作量大；反之，则维修工作量小。第i艘舰艇第k种舰载装备的轻度损伤预计维修工作量的计算公式为:

式中:Dik为第i艘舰艇第k种参战装备的轻度损伤预计维修工作量；Qik为第i艘舰艇第k种参战装备的数量；Pik为第i艘舰艇的第k种参战装备在作战任务中的预计使用频数；βik为第i艘舰艇的第k种参战装备的损伤率；β'ik为第i艘舰艇的第k种参战装备的轻度损伤比例；Tik为修复第i艘舰艇的第k种参战装备轻度损伤所需的平均维修工时。

舰艇参战装备的损伤率和轻重度损伤比例与自身可靠性r和作战任务强度α有关，一般情况下，舰艇装备轻度损伤率和重度损伤率与作战任务强度α的关系如图1所示。

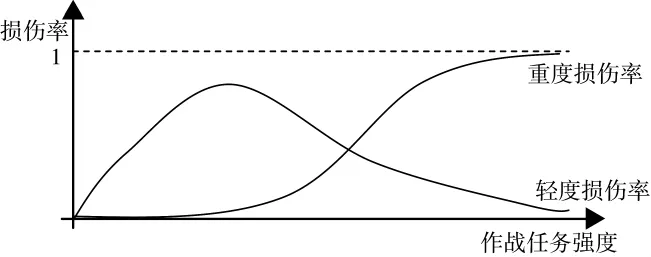
图1 某舰载装备轻度损伤率和重度损伤率与作战任务强度关系

2.1.2 单个伴随保障人员轻度损伤维修效率计算

维修效率受舰载装备种类、伴随保障人员对各装备的维修专业化程度等因素的影响，不同伴随保障人员对不同舰艇不同装备的维修效率各不相同。第j名伴随保障人员对第i艘舰艇第k种装备的维修效率计算公式为:

式中:Vikj为第j名伴随保障人员对第i艘舰艇第k种参战装备的维修效率；θikj为第j名伴随保障人员对第i艘舰艇第k种参战装备的维修专业化水平系数；vj为第j名伴随保障人员每天维修的有效工时，受人员疲劳程度、战场环境、维修器材、保障设备等因素的影响，伴随保障人员每天维修的有效工时远小于24 h，vj根据伴随保障人员的不同通常取15 h/d～18 h/d。

2.1.3 伴随保障人员轻度损伤合作维修效率计算

一般情况下，由于不同伴随保障人员之间学识、阅历存在差异，默契程度有高有低，任务分工难以达到最合理规划，合作维修效率通常小于各个伴随保障人员效率之和，其值大小与伴随保障人员之间的合作系数有关。

第j和第l名伴随保障人员对第i艘舰艇第k种参战装备的合作维修效率计算公式为:

式中:Vikjl为第j和第l名伴随保障人员对第i艘舰艇第k种参战装备的合作维修效率；εjl为第j和第l名伴随保障人员的合作系数；通常情况下，n名伴随保障人员的合作系数取其平均数，即ε总=（εjl+εjh+εhl+…）/n。

2.1.4 单舰战时轻度损伤累计修复时间计算

舰艇战时伴随保障人员配置方案可以表示为n名待分配伴随保障人员在m艘舰艇（每艘舰艇有w种装备）间配置的向量组合，即:

则该配置方案下，第i艘舰艇的战时轻度损伤累计修复时间ti（可以表示为:

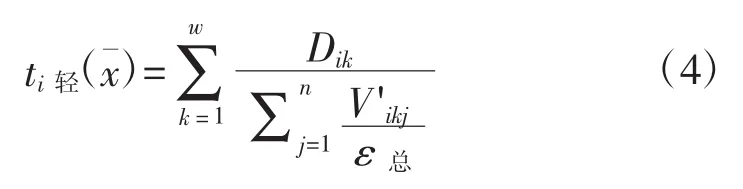
式中，当 xj=i时，V'ikj=Vikj；否则 V'ikj=0。

2.2 单舰战时重度损伤累计修复时间模型

根据假设可知，重度损伤装备由于损伤严重无法完成现场修复，伴随保障人员的主要工作为损伤评估与送修决策，因而其战时累计修复时间由战损评估时间决定。

2.2.1 舰载装备重度损伤概率

在战争持续期间，舰载装备受一次重度损伤则必须脱离战场送修，舰艇重度损伤的概率对作战能力具有重要影响。第i艘舰艇第k种装备的重度损伤概率计算公式为:

其中，Pik为第i艘舰艇第k种参战装备的重度损伤概率；β''ik为第i艘舰艇的第k种参战装备的重度损伤比例，β''ik=1-β'ik。

2.2.2 伴随保障人员重度损伤评估时间

不同伴随保障人员由于专业技能水平的不同，对不同舰艇不同装备的重度损伤评估时间tikj不同，由于战损评估的独立性，伴随保障人员数量的增加对缩短战损评估时间并不具有明显效益，因此，当多名伴随保障人员同时对某舰载装备进行维修时，通常取不同人员战损评估时间的最小值作为伴随保障人员重度损伤评估时间。

2.2.3 单舰战时重度损伤累计修复时间

2.3 目标函数为选择最优的配置方案，使各舰艇战时累计修复时间之和最小

即:

2.4 战时舰艇伴随保障人员组合配置方案必须满足以下约束条件

1）一名伴随保障人员只能保障一艘舰艇，每艘舰艇至少有一名伴随保障人员伴随保障。

2）舰艇核心装备的战损情况直接决定了舰艇战斗力，战时应优先保障核心装备的及时维修。一般情况下，要求核心装备的累计修复时间不超过舰艇总累计修复时间的30%，即:

式中:ti动（为在人员配置方案下，第i艘舰艇核心装备的累计修复时间；ti（）为在人员配置方案下，第i艘舰艇的累计修复时间。

3 混合遗传算法实现

根据上述分析，配置方案模型包含信息多，约束条件复杂，不同的人员组合方式具有离散型、无规律的特点［6-12］。本文采取结合模拟退火算法的混合遗传算法解决此类问题，其运行流程如下页图2所示。

3.1 编码方案

混合遗传算法染色体采用实值编码，每条染色体表示一个舰艇战时伴随保障人员配置方案，基因的个数即待配置人员总数，每个基因值表示对应伴随保障人员所保障的舰艇编号，如图3所示。

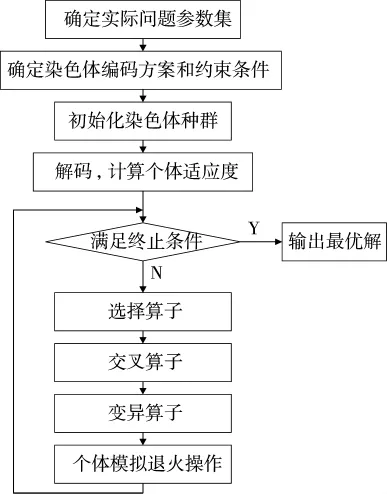
图2 混合遗传算法操作流程

图3 单个染色体基因编码

3.2 约束条件处理

由于每名伴随保障人员不能同时保障两艘舰艇，在编码和解码的过程中应保证每条染色体都有可行解，即每艘舰艇至少有一名伴随保障人员实施保障，因此，每条染色体基因值的集合应包含所有舰艇编号。此外，人员配置方案必须保证各舰艇核心装备的累计修复时间不超过总累计修复时间的30%。

对于不符合约束条件的染色体，引入罚函数:

通过定义罚函数的值等于种群可能的目标函数最大值，以极大降低这些个体的适应度。

3.3 适应度评估

寻找最优的战时舰艇伴随保障人员配置方案即求解目标函数的最小化问题，个体的目标函数越小，其适应度越大，由于MTALAB算法可以直接求解最小化问题，因此，适应度函数可以直接设定为:

3.4 选择算子

设群体的大小为M，个体i的适应度为Fi，则个体被选中的概率Pi为:

本文采用最优保存策略进化模型进行优胜劣汰操作，即当前群体中适应度最高的个体不参与交叉运算和变异运算，而是用它来替换掉本代群体中经过变异、交叉等遗传操作后产生的适应度最低的个体。一般情况下，取精英保存率为种群个数的5%，替代率为交叉操作产生的新群体的后20%。

3.5 交叉算子

本文采取全局从搜索能力较强的双点交叉，在以一定交叉概率Pc在个体编码串中随机设置两个交叉点，然后进行两者的基因交换。通常情况下，Pc取 0.4～0.8。

3.6 变异算子

本文采取基本位变异，在每个染色体内随机产生变异点，在变异概率Pm的控制下随机变异为另一基因值（该值在约束条件范围内）。通常情况下，Pm取 0.001～0.1。

3.7 个体模拟退火操作

设置较低的初始温度T=30°，对经选择、交叉、变异产生的子代种群中的每一个个体s，随即产生3个位点，将1位、2位点间的基因与3位、4位点间的基因左右交换，产生新一代个体c，以概率p接受个体s作为下一代群体中的个体，以概率（1-p）接受个体c作为下一代群体中的个体［6］。

其中，

3.8 结束条件

由于战时舰艇伴随保障人员配置的复杂性，本文采取终止代数和适应度变化阈值双重约束的方式作为结束条件。当遗传算法运行指定进化代数时，或当连续几代个体的平均适应度差异小于某一极小的极值时停止运行，将当前群体中的最佳个体作为所求解问题的最优解输出。通常情况下，终止代数Ts的取值范围为100～1 000，间隔代数G取50代，阈值L取1*10-6。

4 实例仿真

执行某作战任务舰艇编队共有5艘舰艇，15名待配置伴随保障人员，k1装备系统为舰艇核心装备系统。利用式（1）、式（3）、式（5）、式（6）计算各舰艇各类装备轻度损伤下的预计维修任务量、不同人员维修效率如下页表1所示，重度损伤概率、不同人员战损评估时间如表2所示。

根据待配置伴随保障人员人数及设置的混合遗传算法，采用MATLAB编程实现运算。其中相关的参数初始化为:初始种群大小S=100，精英保存个数S'=2，交叉概率Pc=0.6，变异概率Pm=0.08，终止代数Tz=500，间隔代数G=50，阈值L=1*10-6，初始温度T=30°。仿真结果如图4所示。

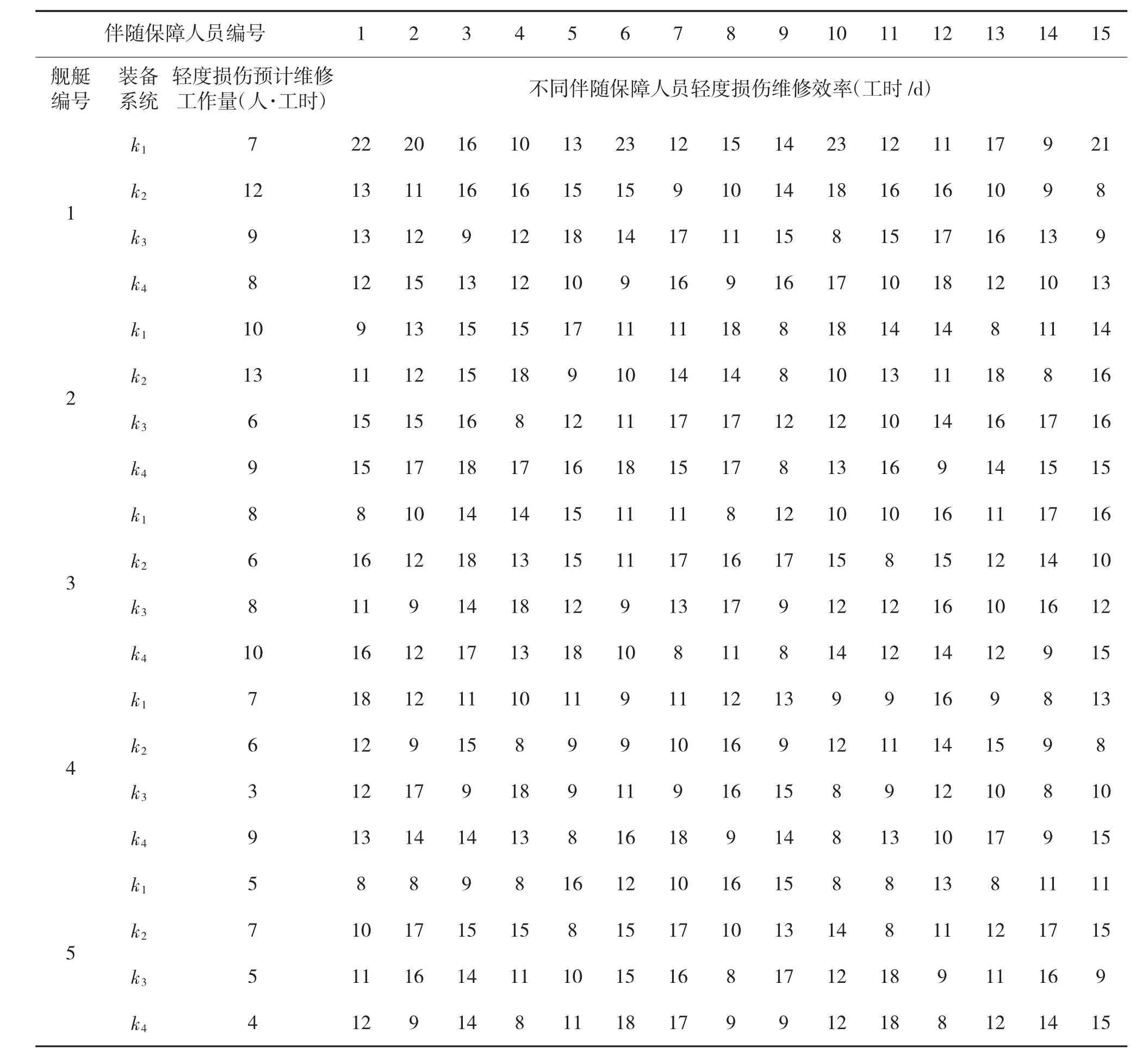
表1 各舰艇装备轻度损伤预计维修任务量及人员维修效率

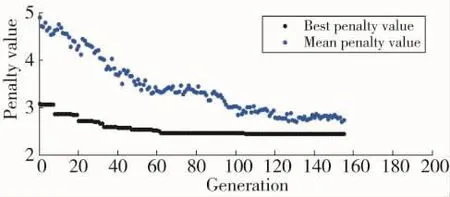
图4 目标函数值随遗传代数进化过程

如图4所示，随着遗传代数的增加，群体平均目标函数值和最小目标函数值呈现递减趋势，且平均目标函数值逐渐接近最小目标函数值。最小目标函数值在105代左右趋于稳定，至第155代进化终止时不再变化，取得最优解。

图5 最终代种群目标函数值分布

图5为最终代种群目标函数值分布，可见大部分个体为最优解个体。同时也有少数个体由于父代交叉、变异呈现较差的表现型，这部分个体的存在，表明混合遗传算法搜索没有陷入局部最优解，体现了混合遗传算法在解决战时舰艇伴随保障人员优化配置问题上具有较强的搜索能力。

由下页图6可知，种群目标函数值标准差随遗传代数的增加而逐渐减小，群体收敛性良好，体现了混合遗传算法在解决战时舰艇伴随保障人员优化配置问题上的较快的运行效率。

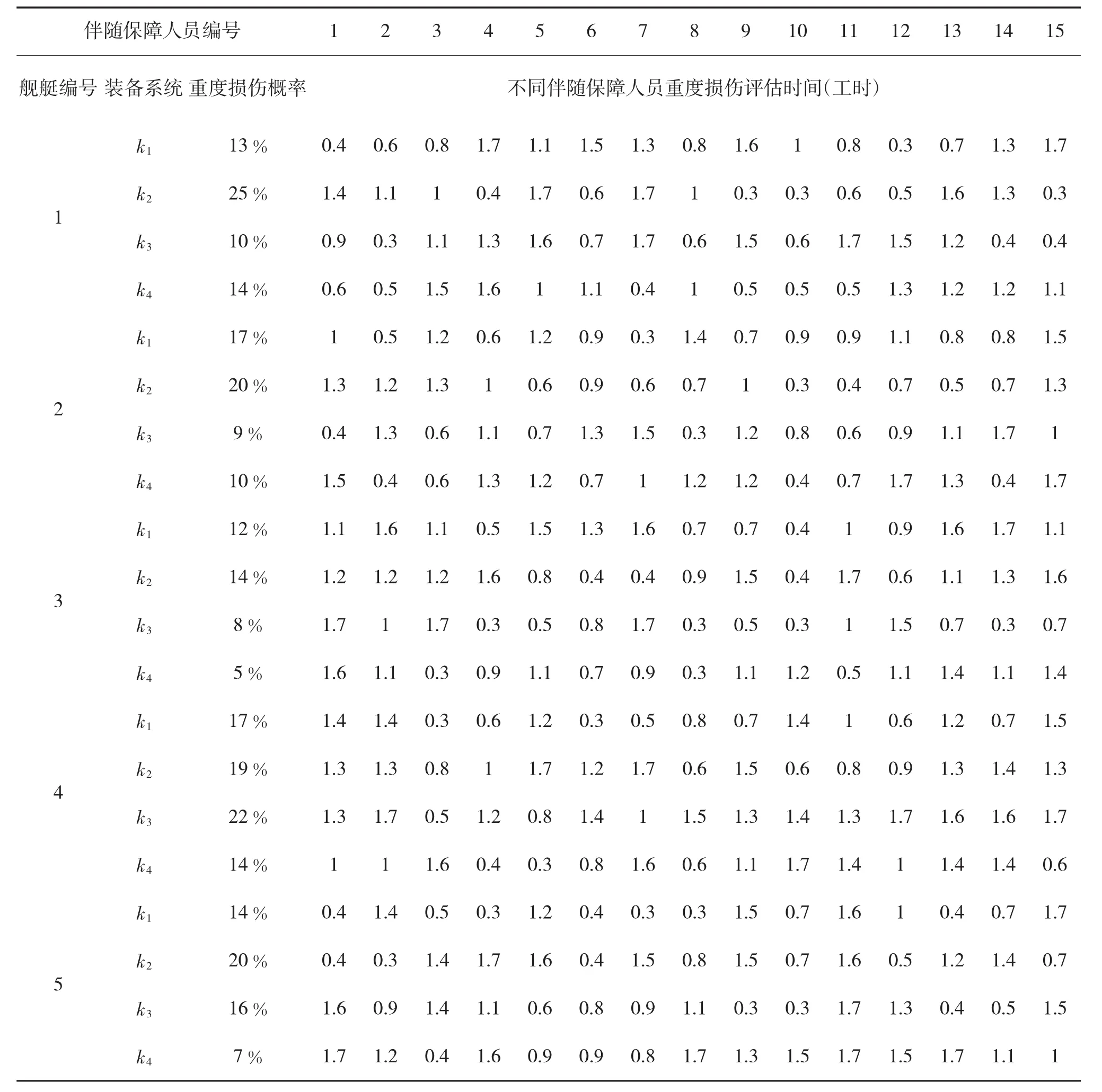
表2 各舰艇装备重度损伤概率及人员战损评估时间

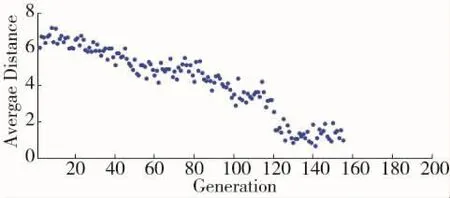
图6 种群目标函数值标准差随遗传代数进化过程

图7 战时舰艇伴随保障人员优化配置最优解

经MATLAB仿真，战时舰艇伴随保障人员优化配置最优解如图7所示，即1、10、15号伴随保障人员负责第1艘舰艇的战时维修保障，2、5、7、13号伴随保障人员负责第2艘舰艇的战时维修保障，8、9、12号伴随保障人员负责第3艘舰艇的战时维修保障，6、11、14号伴随保障人员负责第4艘舰艇的战时维修保障，3、4号伴随保障人员负责第5艘舰艇的战时维修保障。

舰艇两队伴随保障人员配置后各舰艇战时累计修复时间如下页表3所示。