一种改进的GPS/BDS双模系统整周模糊度求解算法
2019-06-13胡朝阳张思远裴炳南
胡朝阳 张思远 裴炳南
1. 大连大学 辽宁省北斗高精度位置服务技术工程实验室,大连116622 2. 泉州信息工程学院 通信与导航技术研究所,泉州 362000
中国“北斗”导航系统的组建完成和美国GPS的技术升级换代为利用多星座组合提高导航系统的定位精度和可靠性提供了条件[1]。模糊度参数的正确固定是利用导航载波相位数据实现高精度定位的关键技术。相对于其他模糊度固定算法,LAMBDA(最小二乘降相关平差)算法是目前公认的最好的模糊度固定算法[2],特别适用于高维模糊度的固定。LAMBDA算法的核心思想是去相关和整数最小二乘搜索[3-4]。另一种模糊度参数固定技术是Bootstrapping(序贯最小二乘平差法)算法,较整数最小二乘搜索简单,但有一定的失败率[5-6];其基本思想是在前面模糊度取整固定条件下,对余下的其他浮点解进行序贯最小二乘平差改正,然后对改正后的值取整。
利用LAMBDA算法漏检率低和Bootstrapping算法计算复杂度低的优点,同时又克服了LAMBDA算法中整数最小二乘搜索计算复杂度高和Bootstrapping算法漏检率高的缺点,本文提出一种新的算法。该算法针对短基线情况下基线向量和整周模糊度的相关性的病态问题,加入数学上的正则化方法调整基线和模糊度参数,改善了协方差矩阵的病态问题,提高了模糊度的搜索效率和成功率。实测导航数据的计算机仿真表明,该方法可以节省时间和提高定位性能。
1 提出算法的依据和问题分析
1.1 双差观测模型
GPS/BDS组合相对定位载波双差方程的数学模型为:
y=Bb+Aa+e
(1)

对方程(1)中的未知向量参数a和b的求解一般可通过3步进行[7]:
1)通过经典的最小二乘法或者卡尔曼滤波方法[8-9]获得模糊度和未知的基线向量坐标的浮点解以及相应的协方差矩阵
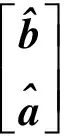
(2)
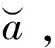
(3)
(4)
1.2 LAMBDA算法
在模糊度的解法中,LAMBDA算法是目前最为熟知和使用的一种方法。LAMBDA算法解决了整数最小二乘问题,并且能够获得载波相位整周模糊度的估计值。
对式(3)进行模糊度搜索求解时,搜索空间可表示为[8]:
(5)
在LAMBDA算法中为加快模糊度固定解的搜索,需要对原始数据进行去相关。Teunissen[4-5]对原始模糊度浮点解做Z变换,以降低其相关性,使搜索椭球更接近球体。其基本算法如下:
1)寻找一个Z矩阵满足[11]:Z中所有元素为整数,det(Z)=±1。
2)对原始模糊度进行如下变换:
(6)


(7)
4)反变换得到原始模糊度的固定解。
1.3 Bootstrapping算法
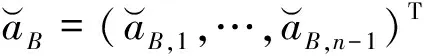

(8)


1.4 病态问题和正则化估计
1.4.1 病态性分析
在式(1)中,令H=[B,A],Y=[b,a],则式(1)可以写成式(9)所示:
L=HY+ε
(9)
式中:L为kn×1维双差观测向量,H为kn×(n+3)维系数矩阵,Y为(n+3)×1维未知向量(包括基线向量和整周模糊度)。
通过加权最小二乘法可得Y的最小二乘解为:
(10)
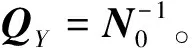

1.4.2 正则化估计
GPS/BDS组合快速定位是一个典型的不适定问题[13]。事实上,在观测历元较少的情况下,由于观测信息不足或者卫星几何形状变化较小将导致法方程的严重病态,正则化方法是求解不适定问题的有效方法,本文对不适定方程加上一个正则条件约束,将问题转化为适定方程,从而获得准确稳定的解。
根据Tikhonov正则化原理,求解观测方程(9)即是寻求满足如下估计准则的解[14-15]:
(11)
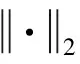
(12)
由式(11)和(12)可以看出,正则化的关键是要确定正则化参数α和正则化矩阵Rα。本文重点是针对LAMBDA快速搜索算法进行讨论,所以正则化参数α和正则化矩阵Rα直接引用文献[15]的讨论结果。
2 改进的快速模糊度搜索算法
利用BDS/GPS组合导航系统的数据实现高精度定位将导致整周模糊度的搜索维数显著增大,从而产生大得多的计算负担;使用LAMBDA算法解决这类问题将可能导致不能快速定位[16]。Bootstrapping算法是直接取整法和序贯条件最小二乘平差算法的结合,考虑了部分模糊度之间的相关性,但是Bootstrapping只是一种近似的估计算法,且只有一定的成功率[8],其正确估计的概率为:
(13)

对式(3)进行顺序的序贯条件最小二乘模糊度求解来实现各分量去相关,进行逆序处理之后的表达式如式(14)[10]:
(14)
该算法并不是所有情形下都能正确估计整周模糊度,其估计正确的概率的上限是一个与模糊度维数n有关的函数,但是该方法比整数最小二乘搜索简单得多,因此确定高精度浮点解和较低精度浮点解的界限是该方法解算的关键。对于满足某种判别条件,采用Bootstrapping进行估计,不满足判别条件,则采用正则化限定后的整数最小二乘进行搜索。这样既提高了搜索效率,又保证了模糊度的求解准确。本文提出的适合BDS/GPS导航数据的解算整周模糊度参数的方法如图1所示。

图1 改进模糊度解算流程图

文献[11]给出了判别式如式(15):
(15)
由于实际的观测数据时间很短,初始的双差整周模糊度的序贯存在不连续情况,对于n≥10的高维模糊度搜索来说,一般式(15)很难满足,此时采用Bootstrapping估计模糊度固定解的成功率比较低。LAMBDA算法对初始模糊度进行了整数Z变换,经过变换之后,以及考虑加入改进的正则化条件,目标函数式(3)转化为:
(16)
与此对应的式(14)变为:
(17)
则与式(15)对应的判别式变为:
(18)

3 数据采集与仿真结果分析
为了验证提出方法的有效性,在2018年7月12日上午10时,利用大连大学日新楼楼顶的两块上海司南导航公司生产的板卡(K528)进行实验数据测量,以双差模型对其进行处理,求得双差模型的浮点解和相应的方差-协方差矩阵,其中,GPS和BDS观测数据的采样间隔设置为10s,观测时间持续分别为10min和20min,获得卫星钟差文件和导航电文文件,其中钟差文件大小为16KB,导航电文大小为4.4MB。在实际的观测情况中,BDS/GPS双模导航系统可视卫星一般保持在13-18颗左右,模糊度维数随历元变化情况如图2所示。
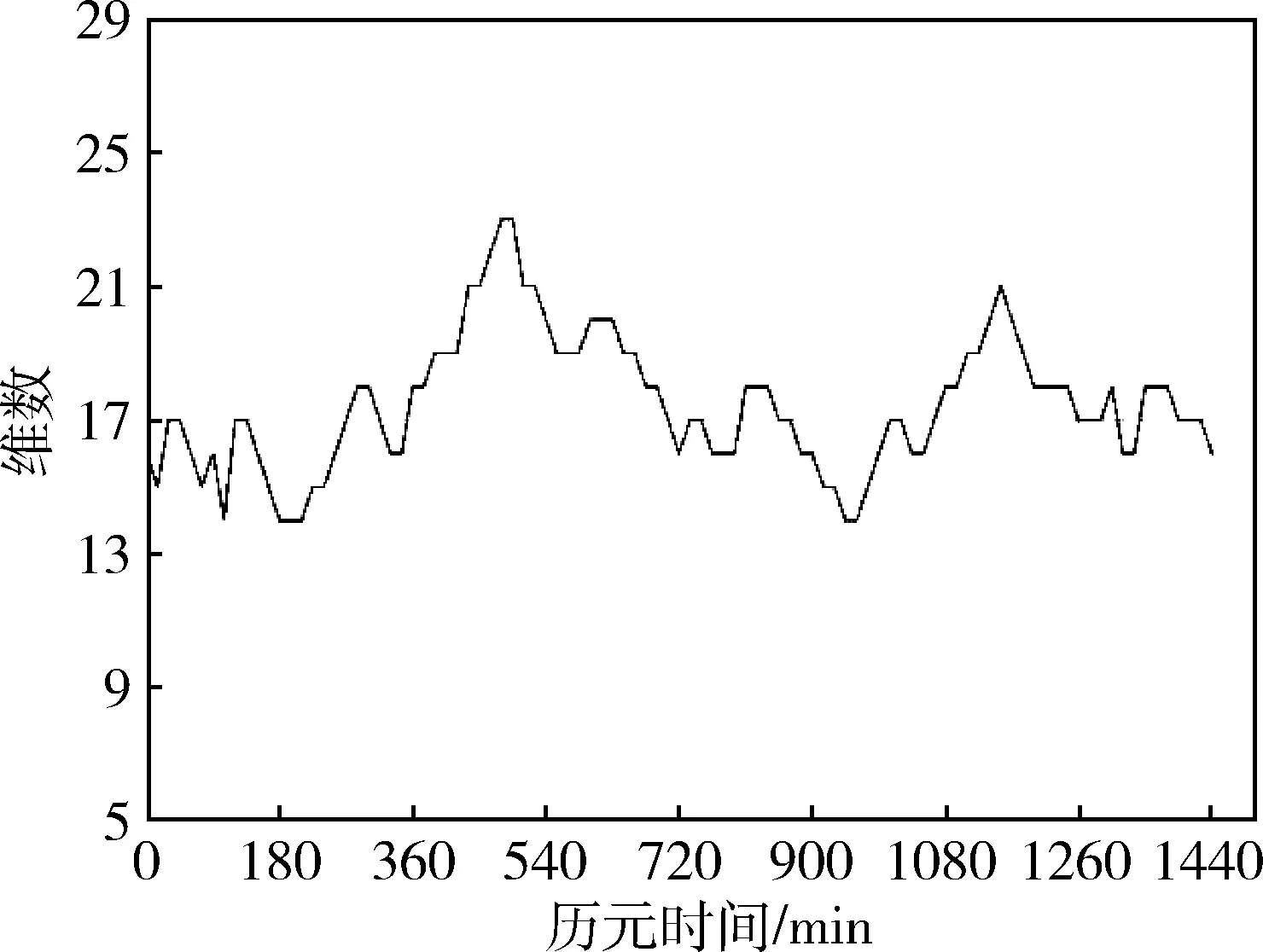
图2 模糊度维数随历元变化
考虑到去相关搜索策略会影响搜索效率,因此,采用Bootstrapping方法、LAMBDA方法和本文提出的新算法(即Modify-search简称M-S算法)对数据进行处理。实验结果分别如表1和2所示。M-S方法中预设的Ratio测试成功率为0.965,由于整数最小二乘解在高维空间中很难直接算出,但是其成功率是最高的,因此设置整数最小二乘的成功率为1。
其中,Ratio值即是整数解中次小与最小验后方差比的检验量,单系统和组合系统的阈值均设为3,则固定率=满足阈值的固定数/总历元数。

表1 不同模糊度搜索时间、成功率比较
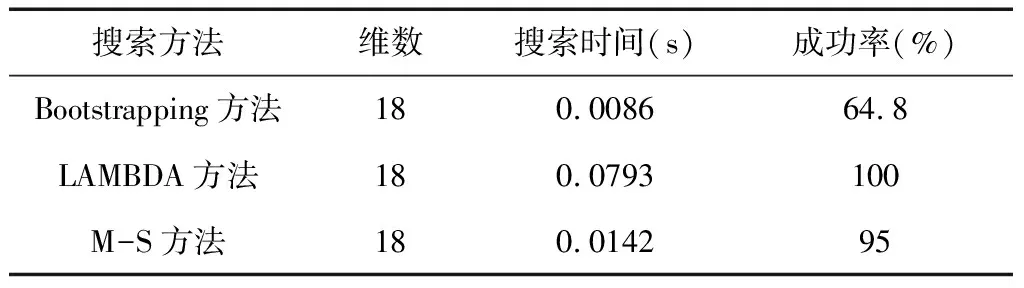
表2 不同模糊度搜索时间、成功率比较
由表1和2可以看出,在组合定位模式中,针对高维模糊度结算来说,模糊度估计效率最高的是Bootstrapping方法,但是其固定成功率最低;LAMBDA算法虽然能够保证解算出整周模糊度,但是其由于方法过于保守,备选模糊度比较多而导致解算效率降低;M-S算法首先通过正则化比例因子改善整周模糊度浮点解,然后通过判别式综合利用Bootstrapping方法和LAMBDA算法,在满足解算模糊度成功率的基础上,一定程度上提高了解算效率,保证了高维模糊度对高精度定位的快速性。
4 结束语
针对BDS/GPS双差观测模型的整周模糊度的解算问题,比较研究了LAMBDA算法和Bootstrapping方法的优点和不足,研究了加权最小二乘方法解算整周模糊度中出现的病态问题,通过引入正则化比例因子改善整周模糊度浮点解,提出了新的整周模糊度求解算法。实验验证和仿真分析表明,改进后的整周模糊度求解算法有效改善了高维情况下的病态性,提高了整周模糊度解算的速度,在双模系统的高精度定位中具有一定的参考价值。
