基于阻力加速度倒数走廊的待飞航程解析预测方法

黄汉斌 杨 业 梁禄扬

1.北京航天自动控制研究所，北京100854 2.宇航智能控制技术国家级重点实验室，北京100854

升力式再入飞行器，相对于传统再入飞行器，升阻比大，机动能力强，可以快速执行天地往返运输和洲际航行任务等[1]，标准轨迹跟踪制导是升力式飞行器再入过程采用最多的制导方法，其中在线轨迹规划技术，可以大大提高标准轨迹跟踪制导的灵活性以及精度，而在线轨迹规划技术最主要的依据是对待飞航程的预测[1-3]。针对待飞航程的在线预测，众多学者进行了广泛而深入的研究，做出了杰出的成果。其中，Ishizuka[4]定义了能量高度，推导出能量高度与航程的微分方程，进而利用龙格库塔积分得到待飞航程；文献[5-7]建立阻力加速度-能量走廊，首先将阻力加速度剖面假定为分段线性函数，进而利用线性函数的特性求出积分计算公式;施健峰等[8]建立忽略地球自转的简化的纵向运动模型，利用数值积分的方法求出待飞航程；曾宪法等[9]将升阻比假定为常数，推导出待飞航程计算的解析公式；而崔乃刚等[10]利用匹配渐进展开的方法推导出纵向运动方程近似解析解，得到纵向运动参数进行待飞航程计算；Yang等[11]选取了阻力加速度-能量走廊的一些离散点，利用离散点三次样条插值获得走廊的解析描述形式，在推导航程解析预测公式时，采用卡尔丹分解的方法对公式进行分解，推导出待飞航程的解析积分公式，由于卡尔丹分解过程较复杂，本文对此进行了省略使得算法进一步简化。

首先分析飞行器无量纲运动模型，将飞行器过程约束和平衡滑翔约束转换成阻力加速度走廊约束，选取一系列节点，将其转换成阻力加速度倒数节点信息，利用三次样条插值建立阻力加速度倒数平滑走廊，进一步推导解析积分公式，实现对待飞航程的解析预测，省去卡尔丹分解过程，并利用该公式计算走廊上下界对应的航程，依据计算结果，推导出与航程相对应的阻力加速度剖面。仿真结果表明，此方法与龙格库塔积分精度误差在10-4m量级，具有较高的近似程度，同时解析设计阻力加速度剖面更简单、可靠。

1 运动模型建立

由于飞行终点时间不固定，需要引入能量的概念，包含高度和速度信息，建立以能量为自变量的无量纲再入飞行器运动模型。这里能量的定义为

e=1/R-V2/2

(1)

建立运动模型之前需要做出一定的假设：

1)不考虑地球自转影响；

2)地球为匀质圆球，不考虑地球扁率；

3)飞行器为无动力质点；

4)再入飞行过程中，弹道倾角为小量，γ≈0。

以能量为自变量的飞行器无量纲运动模型为：

(2)

其中：λ和φ分别为经度和纬度，γ和ψ分别为当地弹道倾角和航向角，σ表示倾侧角。

2 基于三次样条函数描述的阻力加速度倒数走廊

2.1 建立阻力加速度-能量剖面

飞行器滑翔飞行过程中需要满足动压、热流和过载约束，同时为了保证滑翔过程中高度不发生跳跃，需要满足拟平衡滑翔条件。

利用这些约束，以及运动模型，将其转化成阻力加速度-能量走廊约束，其中，动压、过载和热流约束对应阻力加速度走廊上界，拟平衡滑翔约束对应阻力加速度走廊下界。选取n个节点，作为走廊的描述点(如图1)。

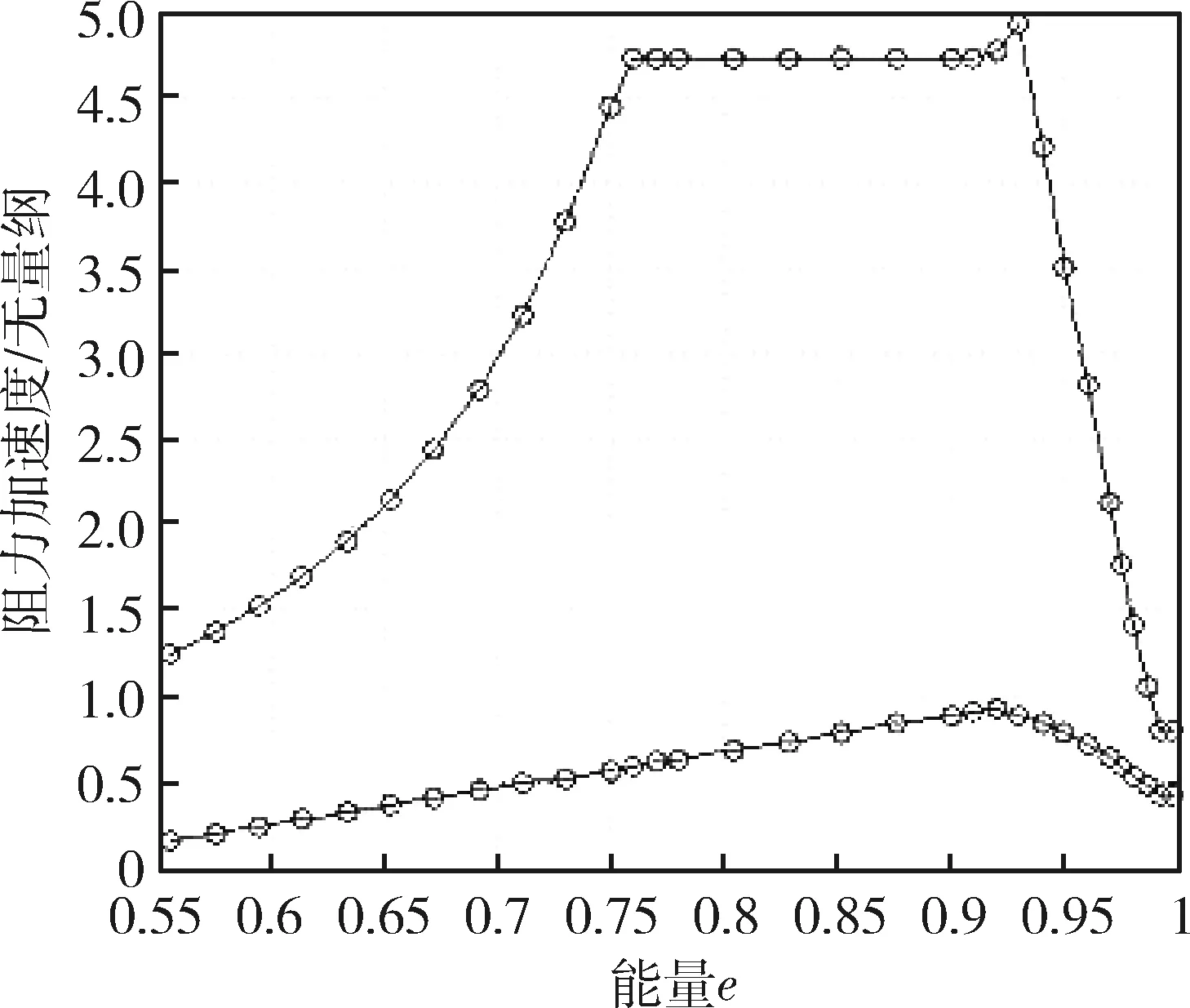
图1 阻力加速度走廊

2.2 三次样条函数描述阻力加速度倒数走廊

利用2.1节得到的阻力加速度-能量节点信息，建立阻力加速度倒数走廊节点信息(图2)，然后利用三次样条函数拟合，计算倒数两点间的函数值，得到2个节点之间的三次函数(式(3))以及阻力加速度倒数走廊(图3)。

(3)

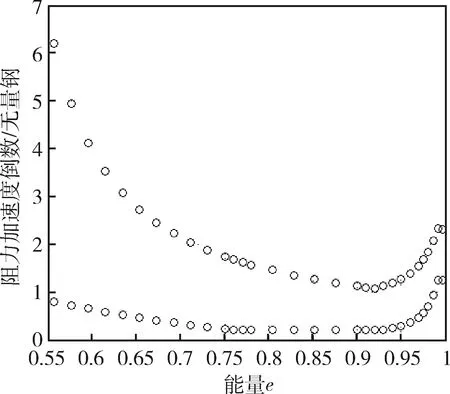
图2 阻力加速度节点倒数

图3 三次样条插值描述阻力加速度倒数走廊

3 待飞航程解析预测

待飞航程定义为当前点地心矢径r和目标点地心矢径rf所形成的大地张角对应的圆弧，式(4)为航程对时间的导数。

(4)

由于假定弹道倾角为小量，同时忽略航向角偏差，引入能量概念，得到航程对能量的导数公式为：

(5)

由于阻力加速度倒数剖面可以描述成三次样条函数，利用式(3)和式(5)，得到待飞航程解析积分公式为：

(6)

(7)

其中，Smax和Smin分别表示待飞航程的上下边界。

4 基于航程计算公式的阻力加速度剖面解析设计

根据以上推导的航程解析公式，可知，在对阻力加速度倒数走廊进行三次样条插值后，其所对应的航程与三次样条拟合出的系数成线性关系，由此可以根据任一在航程边界内的待飞航程S，推导出相应的阻力加速度剖面。

首先，利用式(8)计算与航程上下界之间的关系：

(8)

由式(8)中的ξ计算阻力加速度倒数剖面对应的系数，如式(9)。

(9)

式(9)得到了阻力加速度倒数各段的三次函数系数，即得到了满足航程要求的完整且解析的阻力加速度剖面。

5 仿真验证

利用第3节推导出的公式进行待飞航程解析计算，采用文献[11]中的飞行器参数：

质量m=1000kg，参考面积Sref=3.5m2。升力系数和阻力系数采用简化形式，其中升力系数:

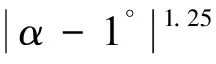
阻力系数：

攻角α采用与速度相关的固定剖面：

(10)

走廊边界所对应的约束：

1)驻点热流约束：

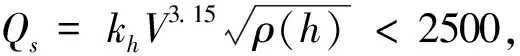
2)动压约束：Q<15000Pa；

3)过载约束：Nmax<5g。

再入过程初始和终端信息如表1。

表1 再入初始和终端约束

仿真结果如图4～7。

图4 解析计算与龙格库塔方法对比

图5 解析积分与数值积分偏差

图6 阻力加速度剖面

图7 航程-能量剖面

其中,图4的方形节点所表示的曲线是本文方法解析积分得到的待飞航程，圆形的是数值积分得到的待飞航程，两者基本重合。为了进一步比较两者偏差，在图5中给出了上下界数值积分和解析积分的偏差，同时列出了文献[11]中的偏差，2种方法与龙格库塔积分的误差在同一水平上，为10-4m级别，本文采用的方法省去了卡尔丹分解过程，形式上更加简单。

利用本文的解析预测航程的方法可以设计满足航程要求的阻力加速度剖面。分别选定待飞航程S=1500km，2000km，3000km及4500km，利用式(8)和(9)进行仿真计算。图6给出了相应的阻力加速度剖面，图7给出了其所对应的航程，仿真结果与航程要求一致且满足阻力加速度走廊约束。

6 结论

将飞行过程约束和平衡滑翔约束转换成阻力加速度倒数-能量的约束，利用三次样条函数对阻力加速度倒数-能量走廊进行拟合，并推导出待飞航程的解析计算公式，利用解析航程预测公式进行仿真，与龙格库塔积分精度一致，同时根据预测结果可以解析设计阻力加速度剖面，形式更加简单，计算效率较高，有工程应用的潜力。