永磁同步电动机转子系统的模态分析计算
2019-06-13
(广东工业大学,广东广州 510006)
0 引言
电机是一个包含定、转子在内的机电耦合系统。转子作为各种旋转机械的关键部件,电机转子的振动特性直接影响到转轴的可靠性和电机的工作寿命的长短。—般情况下,转子根据它自身的变形属性,变形系数低称为刚性转子反之称为柔性转子。振动主要在其临界转速附近比较显著,为确保调速范围内可以避免共振,应保证其临界转速尽量远离正常工作转速。对于刚性转子,工程上希望它的工作转速小于一阶临界转速,柔性转子则希望它工作转速大于一阶临界转速。因此准确计算转子结构的模态特性对于选取转轴材料以及排除电机共振故障有很重要的现实意义[1]。
现如今应用于计算临界转速的方法有很多,包括有:有限元法、有限差分法、传递矩阵法以及结构修正法。但由于影响临界转速的因素很多,要想获得更贴近实际表现的临界转速,依然是目前所需要研究的重点之一[2~4]。
文献[5]针对永磁同步电机转子的磁钢保护套对转子临界转速的影响进行了模态分析,验证有限元方法的有效性。文献[6]针对滑动轴承对转子系统的运动情况影响,讨论了集中圆盘与轴段耦合处不同处理方式对自然频率的影响,得出滑动轴承-转子系统的结构的处理方式会影响临界转速的结论。文献[7]讨论了刚性联轴器以及弹性联轴器对转子-轴承系统的模态频率影响,得出联轴器的特性对低阶模态影响幅度不大的结论。文献[8]讨论了结构参数对转子-轴承系统临界转速的影响,研究表明增大系统的阻尼对过临界运行的柔性转子系统跨越各阶临界转速很有利。
本文主要研究轴承对转系统的影响,包括自由状态与轴承支承状态的对比,以及对称轴承支撑与非对称轴承支撑下的转子系统模态对比。基于有限元法能够确保模型的完整性和分析的准确性,可以进行复杂转子系统的临界转速计算,本文主要选择有限元法对转子模态进行计算。
1 转子动力学基本原理
首先以单圆盘转轴为例,通常转轴的两个支点在同一水平线上,未变形时,中心线应该保持水平状态,但是由于转盘的重量,会使转轴发生轻微变形,并且该变形会随着转速的增加产生的离心力导致转轴的进一步变形。由图可以看出,转轴将会发生弯曲变形,在旋转时作圆周运动,而圆盘作平面的运动。在简化计算中不考虑轴的自重,圆盘位于轴的中部集中重量为m。根据一般工艺水平,圆盘的重心A偏离于轴心O一个偏心距h。轴的弹性弯曲刚度为k,圆盘的回旋振幅为y,转动角速度为ω。单圆盘转轴见图1。

图1单圆盘转轴
在圆盘转动时,弹性力平衡于惯性力,有
kx=m(y+h)ω2
(1)
可推导出振幅y的表达式
(2)
当k=mω2,y将会无限大,则有
(3)
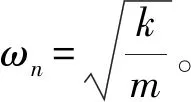
电机转子作为旋转运动部件,满足一般性的运动方程,可得出如下转子动力学方程
(4)
式中,m—转子质量;k—轴承刚度;r—阻尼系数;rq—转子系统内部阻尼;x、y—位移向量;F—激振力向量。
可以将转子位移表示出
u(t)=x(t)+jy(t)
(5)
转子自由旋转时有,带出(5-4),可得

(6)
对上式进行拉普拉斯变换并进行求解有
ms2+rs+k-jΩrq=0
(7)
(8)
忽略阻尼对于转子自由旋转状态下,即r=0。上式可变为
(9)
式中,ω1—转子正进动模态频率;ω2—反进动模态频率。
所谓正进动,是转子在不平衡力作用的旋转下的涡动方向与自转方向保持一致。若不一致则称为反进动。
根据转子的各阶模态频率可以得到转子的临界转速,其表达式为
np=60f
(10)
式中,np—临界转速;f—模态频率。
2 转子模态的有限元计算
永磁同步电动机转子结构根据永磁体的安置形式不同,分为表贴式以及内置式。本文的研宄对象是表贴式永磁同步电机转子结构,主要包括转子铁心、永磁体和转轴。永磁同步电动机的模态参数比较复杂,为了得到准确的磁钢、转子铁心、转轴的有限元模型, 通过Maxwell软件导出3D模型如图2,并将该模型导入 ANSYS Workbench Modal 模块中,以仿真分析各阶次的径向振型与固有频率。

图2转子系统3D模型
要得到准确的模态参数,不仅要在模型完整表现出电机本身的机械结构,还要考虑其各机械结构本身的材料密度、弹性模量以及泊松比,所以在对转子结构进行有限元模态仿真前,要对各部件材料进行正确定义。该永磁同步电动机转子结构的材料参数如表1所示。
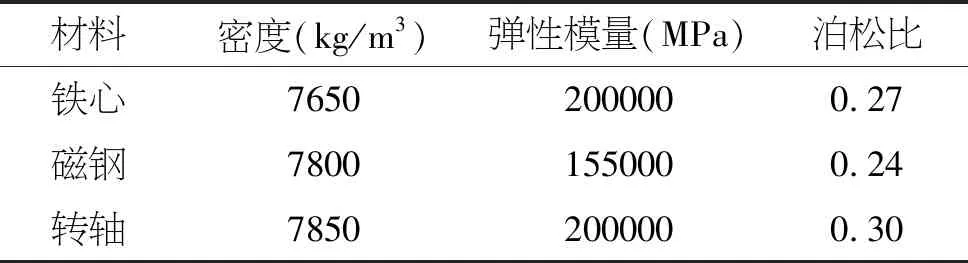
表1 转子系统结构材料属性
通过workbench软件对转子模型进行模态分析,由于本文主要研究自由状态下与轴承支撑状态下临界转速的变化,而转子的前三阶振型形状变化不大,这里模态振型以自由状态下转子振型为例子。转子模态振型图见图3。

图3转子模态振型图
由于转子具有旋转的特质,旋转的转子产生的陀螺力矩会影响转子的模态频率数值上的变化,称为陀螺效应。“陀螺效应”是制约转子动力学的一个“瓶颈”问题,解析法对其一般很难考虑,利用三维有限元法可以充分考虑其对转子模态特性的影响。
2.1 自由状态下转子临界转速分析
永磁电机转子在无外部约束条件下的系统坎贝尔图如图4所示。从中可以看出在0~4000r/s范围内,没有达到一阶转速。

图4 自由状态转子系统坎贝尔图
2.2 转子在轴承支撑下的临界转速分析
转子系统轴承支撑3D模型如图5所示。永磁电机转子在轴承距离不对称条件下的系统坎贝尔图如图6所示。在(0~4000)rad/s内,有两个临界转速点,从表 2 可以得到一阶临界转速为1379.2rad/s、1657.5rad/s。

图5转子系统轴承支撑3D模型


图6 轴承支撑状态转子系统坎贝尔图
2.3 转子在对称长度轴承下的临界转速分析
转子系统对称轴承支撑3D模型见图7。永磁电机转子在轴承距离不对称条件下的系统坎贝尔图如图8所示。在(0~4000)rad/s内,有两个临界转速点,从表 2 可以得到一阶临界转速为1537.9rad/s、1806.1rad/s。

图7转子系统对称轴承支撑3D模型
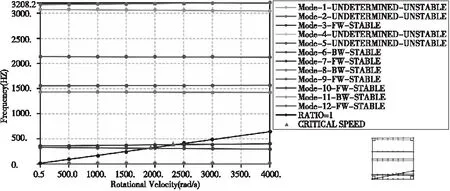

图8 对称轴承支撑状态转子系统坎贝尔图
3 结语
本结构通过对永磁同步电机的转子结构分析,考虑轴承的影响,采用ANSYS workbench软件对转子进行模态分析,计算自由状态下,轴承支撑状态下及对称轴承支撑状态下三种情况,得出以下结论。
针对一般调速永磁同步电机,由于转子与轴承材料可以提供足够刚度,在轴承支撑状态下,转子一阶转速远高于其额定转速,不会产生共振。但参考本研究所得数据,对于高速永磁同步电机而言需要考虑转子系统的临界转速。
转子系统在自由状态与轴承支撑状态下,由于轴承的支撑,可以大幅度降低转子系统的低阶模态频率,所以在研究转子系统临界转速时,应该充分考虑轴承的影响。
转子系统的模态频率与轴承位置有关,在双轴承距离转子铁心对称情况下与不对称轴承相比,对称轴承能增加转子系统稳定性,低阶模态频率均比不对称轴承高,在高转速永磁同步电机转子系统设计时,为提高轴承支撑下转子系统临界转速,应该尽量保持双轴承对称。
