同步电机定子磁势转速差异及阶梯波周而复始的直观解释
2019-06-13
(华南理工大学电力学院,广东广州 510640)
0 引言
同步机转子磁场之旋转源于原动机驱动,因而转子谐波磁势的转向、转速,与基波磁势的相同,都是同一方向的同步速;而同步机定子磁势之旋转源于定子电流的交变,定子谐波磁势的转速,与基波的不同,有的转向甚至还相反。定子ν(希腊字母,常用来表示谐波次数)次谐波磁势的转速是基波的ν分之一,一般的电机学教科书[1~11]都对此进行了严格的推导。
这里提出的问题是:(1)严谨的推导往往失之于抽象,让人失去直观,对推导结果陷于死记硬背。那么,严谨的同时,能否有一个直观的解释呢?(2)不作傅里叶分解时,定子三相合成磁势是阶梯波。当定子电流变化一个周波后,定子三相合成磁势又重复当初的阶梯波。如果基波、谐波的转速不同,有的转向还相反,那么,以不同转速、转向转动的各成分(基波、谐波)又怎么会合成得到和当初一样的阶梯波呢?
这一现象如何理解?本文即作此一试。
说明:(1) 同步机乃同步电机之简。异步机乃异步电机之简。(2) 磁势乃磁动势之简。(3)本文中磁场以磁势的面貌出现,因而,磁势、磁场不加区分。
1 谐波转速为基波转速ν分之一的直观解释
1.1 对称三相电流和对称三相绕组
不妨做一个纸面上的实验。给定一组对称三相电流,如式(1)、图1所示。两个对称三相绕组如图2所示。
(1)
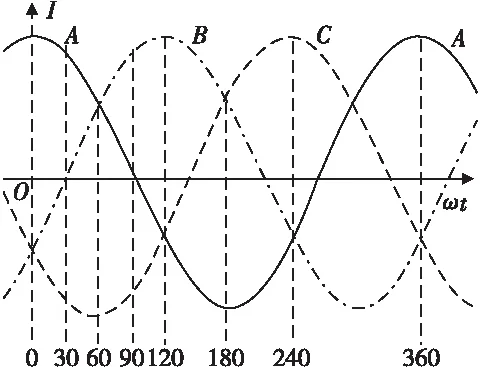
图1对称三相电流的变化波形
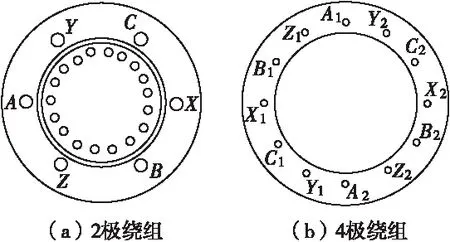
图2对称三相定子绕组
在以下各图中,三相电流皆以尾进首出为正方向。
1.2 对称三相电流通入对称三相2极绕组的情形
对称三相电流通入图2(a)所示2极绕组时,三个典型瞬间的磁场如图3(a)、图3(b)、图3(c)所示。

图3三个典型瞬间的2极定子磁场图
1.3 对称三相电流通入对称三相4极绕组的情形
为图面清晰,未画出转子。当三相电流通入图2(b)所示4极绕组时,三个典型瞬间的磁场如图4(a)、图4(b)、图4(c)所示。图面上的数字表示钟点数,它形象地反映出磁场移动的情况。
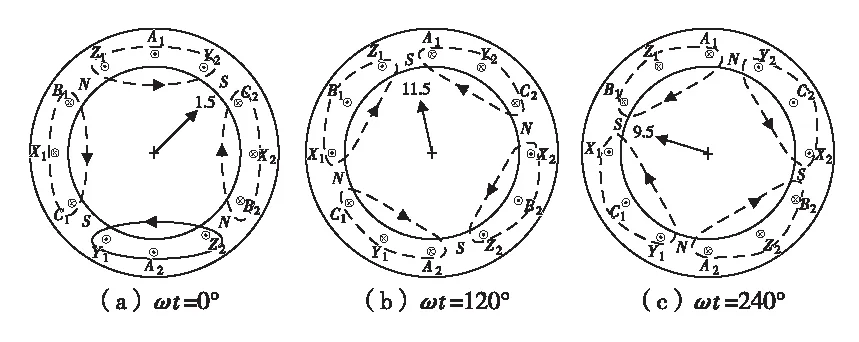
图4三个典型瞬间的4极定子磁场图
1.4 对2.2和2.3中图观察的结论
考虑到4极时,电角度是机角度的2倍,故,对图3、图4的观察,可以得到如下3个定律。
(1)磁场转向定律:磁场按照电流的相序,即取得最大值的先后顺序,旋转。
(2)磁场转速定律(比频速公式):电流变化多少电角度,磁场就转过多少电角度,即电流变得快,磁场就转得快,亦即磁场转速与电流频率成正比。考虑到机角度为电角度的p分之一(p为极对数)可知,磁场的旋转速度与极对数成反比。通过作图,这一结论不难推知p为任意自然数情形。考虑到频率以秒计时,转速以分计时,磁场的转速可以写成
(2)
不计时间单位的差别时,磁场转速就是“比频(specific frequency)”,即单位极对数下的频率。因此,可把由式(2)决定的转速,称为“比频速”。
教科书[1~11]都把磁场转速称为“同步速”。此乃因为同步机时,转子的转速与定子磁场的转速同步。从同步机的角度看,这无可厚非。但从物理量的物理内涵角度看,则“比频速”比“同步速”要好些。因为“比频”反映了磁场转速的内在的决定因素-电流频率和磁场极对数。
“同步速”不仅没有反映磁场转速的物理内涵,而且,它还只适于同步机,而不适于异步机。因为异步机情形,如果转子速度达到同步,那么,就不成其为异步机了。
(3)磁场幅值位置定律:某相电流取得幅值,则,磁场幅值就位于该相轴线上。
1.5 梯形波、基波二者转速的等价性
注意到2.2和2.3中所画磁场皆未进行傅里叶分解,即为阶梯波,其主要成分为基波。基波和其所属阶梯波,二者在空间的振荡频率相同,因而,在空间的移动速度亦相同,即如式(2)所示。
由于基波和阶梯波的幅值都位于相绕组的轴线上,故无论对基波还是阶梯波,磁场幅值位置定律都是成立的。
设基波极对数为p,那么ν次谐波的极对数就是νp。据式(2)可知,
(3)
可见,ν次谐波磁场的转速为基波磁场转速的ν分之一。
2 谐波转速各异时合成阶梯波仍然周而复始的直观解释
为说明问题又不失一般性,设阶梯波磁场为2极,且仅由基波和5次谐波构成,如图5所示。该图中横轴均分为30小段,每一小段占120机械角。五次谐波的周期为720°机械角。
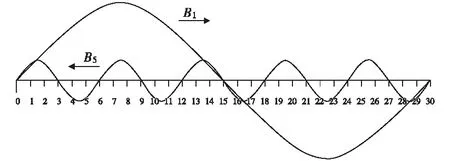
图5基波和五次谐波的移动
设图5所示为ωt=0°时的波形。下面的分析,请注意图5是一个圆周的展开图。
(1)当时间经过一个周期后,基波B1向右移动360°电角,故B1仍然回到原来位置。
(2)当时间经过一个周期后,五次谐波B5向左移动360°电角,相当于B5向左移动72°机械角,亦即图5中B5的每一个周波都往左移动了一个周波,最左边的周波移到最右边,整个波形没有变化。
(3)据(1)、(2)可知,当时间经过一个周期后,图5中的波形,无论B1还是B5,波形都保持不变。因此,它们的合成波形也保持不变。同理,可说明阶梯波由基波和其他次谐波组成时的情况。
综上可知,虽然傅里叶分解得到的各次谐波转速各异,有的甚至方向相反,如五次谐波,但,磁场阶梯波的波形仍然能够周而复始。
3 结语
(1)直观解析了:定子ν次谐波磁势的转速是基波的ν分之一。
(2)直观解析了:虽然傅里叶分解得到的各次谐波转速各异,有的甚至方向相反,如五次谐波,但,定子阶梯波的波形仍然能够周而复始。
(3)诉诸直观,能够帮助理解和记忆,是抽象分析问题的很好的补充。
(4)对“同步速”这一传统术语提出了批评,指出它仅适于同步机,并提出了“比频速”术语,以补其不足。比频速不仅适于同步机,而且适于异步机。
