太沙基地基极限承载力的三剪应力统一强度理论解

高江平，胡海波，孙世界，王泽普

(长安大学 特殊地区公路工程教育部重点实验室，陕西 西安 710064)

工程领域对地基承载力的探究是岩土工程学科一个重要的问题，因为地基稳定性的影响因素很多，对工程的各项性能评估具有重要的意义.

强度准则揭示了物体受力状态下产生塑性形变和损坏的现象.目前，岩土材料研究中多采用Terzaghi准则和Mises准则解决实际问题[1].但是在实际运用中发现，其分别存在各自的局限性.前者在实际运用中忽视了中主应力的作用.而后一准则比较复杂，不存在相关性，实际运用中通常只能采用数值法进行求解.

1943年，太沙基首次依据Mohr—Coulomb理论提出了地基承载力公式[1]，沿用至今.但是，在运用中发现，太沙基地基最大承载力公式未考虑中主应力，因而无法彻底揭示地基的真实破坏状况.

本文根据三剪统一强度理论，可求得基于此理论下的太沙基地基极限承载力值，并探究权系数b、c对其的影响.

1 三剪应力统一强度理论[3]

该理论认为：菱形十二面单元体上的三个主剪应力(τ13、τ12、τ23)与三个正应力(σ13、σ12、σ23)构成的函数关系式达到某一极限值时，材料产生损坏.其数学公式为

F=τ13+bτ12+cτ23+β(σ13+
bσ12+cσ23)=f

(1)

也可将式(1)表示成以下形式：

F=τ13+βσ13+b(τ12+βσ12)+
c(τ23+βσ23)3=f

(2)

式中：β为在正应力作用下材料损坏的强度影响参数，b为在τ12和σ12作用下材料损坏的影响系数，c为在τ23和σ23作用下材料损坏的影响系数，b与c均在0～1范围内取值，f为材料强度参数.

建立了此理论下的内摩擦角φs、粘聚力cs公式[3]：

(3)

(4)

(5)

式中：φ0和c0为Mohr-Coulomb理论下的内摩擦角和黏聚力，σ2=m(σ1+σ3)/2，且m在0到1之间取值，当材料处于弹性阶段时，m可取值为2v，其中v表示材料泊松比，当材料处于屈服变形状态时，m→1.

2 太沙基地基承载力的三剪统一强度理论解

2.1 基本假设

(1)假设地基作用面不光滑，摩擦力很大.整个地基产生贯穿至基底的剪切破坏，产生持续的滑动，基底下局部土体与基础同时移动，从而该土体一直保持弹性状况，区域Ⅰ为弹性楔体.该局部土体与滑动土体分界线用ab表示，并假设分界线ab与基础底平面的夹角用ψ表示，如图1所示.

图1 基底粗糙情况下的滑动面形状Fig.1 Sliding surface shape of rough base

(2)径向剪切区域Ⅱ与朗金被动区域Ⅲ形成滑动区域，且所有滑动区的土体(区域Ⅰ除外)均保持在塑性平衡状况，区域Ⅱ的界线bc用以下公式表达：

(6)

式中：r0为初始位置矢量，θ为任意位置矢量r与初始位置矢量r0的夹角.

区域Ⅲ的界线cd是一条直线，与水平面的夹角为45°-φs/2.

(3)考虑在基础两侧地基上施加均布超载q=γD，来抵消土体抗剪强度的影响.

2.2 地基极限承载力公式

由2.1中的假设条件，通过图2所示的区域Ⅰ三角形aba1的平衡关系，推导出整个剪切破坏情况下的极限荷载表达式：

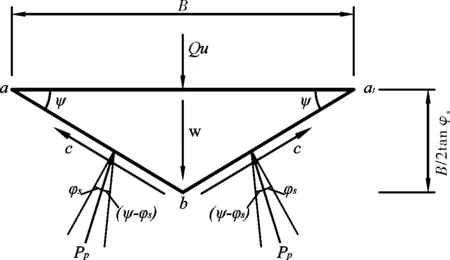
图2 区域Ⅰ弹性楔体受力示意图Fig.2 Stress diagram of elastic wedge in Region I

(7)

式中：γ为基础以下土体的重度，B为基础底部宽度，c0和φ0为基础以下土体的抗剪强度参数；作用力Pp为一合力，由基础以下土体的粘聚力c0、基础以下土体的重度γ产生的被动土压力和超载q组成，其作用面为区域Ⅰ的分界面ab，即

PP=PPc+PPq+PPγ

(8)

(9)

Kpγ为基础以下土体的重度γ所产生的被动土压力的作用系数，确定Kpγ需要采用试算方法.

联立公式(7)与公式(9)推导得出：

(10)

其中：

(11)

式中，Nc、Nq、Nγ为无法量化的承载力系数指标，只和φ0有关.

式(10)是以基底粗糙为条件推导出的，并且图2中ψ是未知的.故作如下假定：

(1)假定基础完全粗糙.此时作出如下假定：认为ψ=φs，基础底部滑动面形状如图3.

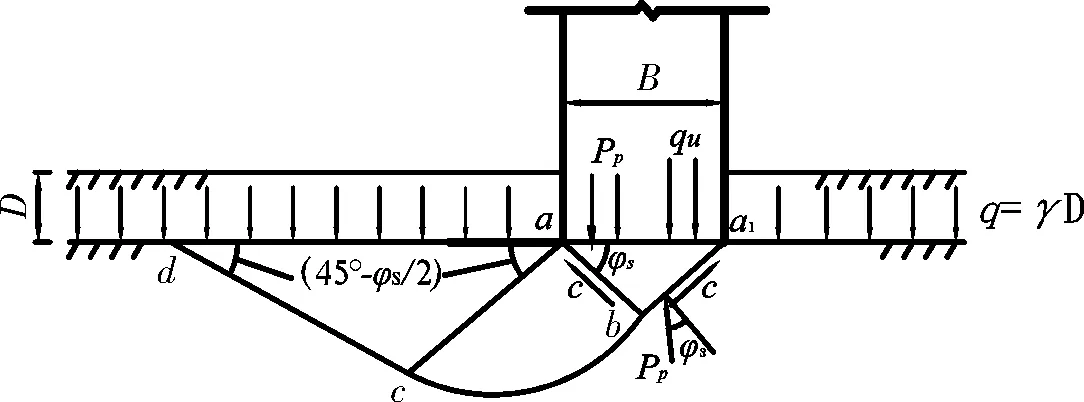
图3 基底完全粗糙情况下的滑动面形状Fig.3 Sliding surface shape of completely rough base

则可将式(11)的形式表示成如下情形；

(12)

从式(12)可知：系数Nc、Nq、Nγ均受到基础以下土颗粒间摩擦角φ0的影响，一般需要通过试算确定被动土压力系数Kpγ.

工程运用上为了方便，对于系数Nγ，往往联合太沙基经验公式，采用如下式确定：

Nγ=1.8(Nq-1)tanφs

(13)

(2)假定基底完全光滑.则区域Ⅰ的土体状态转变成朗金主动状态，从而使得区域Ⅰ与区域Ⅱ和区域Ⅲ共同构成一个完整的滑动区，这时区域Ⅰ的界线ab与水平面的夹角ψ(如图3～图4所示)有如下表达式：

将ψ代入式(11)中，可分别得到此条件下的系数Nc、Nq、Nγ.

火箭测试厂房平开大门(下简称大门)能够实现大门的水平方向移动,从而实现矩形门洞的闭合与打开,是各航天发射场广泛使用的一种特种机械设备,它具有抗冲击能力强、工作可靠性高、制造工艺相对简单等优点.但是由于厂房需求不同,加之不同时期的设计能力、计算能力也千差万别,造成发射场大门形式多样,装备化保养困难.随着航天发射场的不断发展,传统意义上粗大笨重、操作复杂、维护困难的厂房大门已经无法适应发射场特种设备“三化”的要求,结合某发射场火箭厂房扩建工程新建大门,对发射场现有各种大门的功能和结构模式，进行统计分析和梳理分类,从大门系列化的角度,本着有限目标,重点突出的原则,研究大门的模块化设计方法.

图4 基底完全光滑情况下的滑动面形状Fig.4 Sliding surface shape of completely smooth base

3 算例

现有某地基，土的重度γ=19.5 kN/m3，土体均匀，为粘性土.经固结不排水条件下快速剪切试验，测得c0=20 kPa，φ0=22°.地基土上埋置一长条基础，深度3 m，宽度4 m.

根据以上已知条件，分别基于四种不同的理论，求解地基极限承载力值，并进行比较分析.

3.1 经典太沙基公式解[1]

3.1.1 当基础底部为完全粗糙状态时，根据题设条件φ0=22°计算得出承载力系数Nc=20，Nq=10，Nγ=7.最后解得地基极限承载力qu=1 258.0 kPa.

3.1.2 当基础底部为完全光滑状态时，根据题设条件φ0=22°计算得出承载力系数Nc=16.88，Nq=7.82，Nγ=4.96.最后解得地基极限承载力qu=988.5 kPa.

3.2 双剪强度理论解[6,8]

地基承载力达到其极限值，此时地基处于屈服破坏的临界状态，中间主应力参数m=1.

当基础底部为完全粗糙状态时，根据题设已知条件，计算得到承载力系数Nc=27.5，Nq=14.78，Nγ=12.3.从而最终解得极限承载力为qu=2 017.7 kPa.

3.3 双剪统一强度理论解[5]

地基承载力达到其极限值，此时地基处于屈服破坏的临界状态，此时中间主应力参数m=1.

当基础底部处于完全粗糙时，假设系数b(0≤b≤1)分别取0、0.2、0.4、0.6、0.8、1，解得极限承载力如下表1所示.

表1 完全粗糙基底条件下的地基极限承载力值

当基础底部处于完全光滑状态时，假设系数b(0≤b≤1)分别取0、0.2、0.4、0.6、0.8、1，解得极限承载力如下表2所示.

表2 完全光滑基底条件下的地基极限承载力值

3.4 三剪应力统一强度理论解

地基承载力达到其极限值，此时地基处于屈服破坏的临界状态，此时中间主应力参数m=1.利用上文中推导的公式分别计算.

(1)当基础底部处于完全粗糙状态时，系数b与c分别在0～1之间取值，从而解得相应的极限承载力值，如表3所示，并绘制了此条件下系数b、c与qu之间的关系图，如图5所示.

表3 完全粗糙基底条件下的地基承载力值

图5 完全粗糙基底条件下系数b、c与qu之间的关系图Fig.5 Correlation graphs between b, C and qu on completely rough base

从表3及图5中可以看出地基极限承载力qu受到b、c取值的影响，b、c取值越大，则qu越大.由表3的计算结果与3.1.1的结果相比可知，本理论的承载力值均大于经典太沙基承载力值；与3.2.1的结果相比可知，当b=1，c在0～1之间取值时，本理论的承载力值均大于双剪强度理论的承载力值；与3.3.1相比，当c=0，b在0～1之间取值时，式(1)蜕化成双剪统一强度理论，本理论的承载力值即为双剪统一强度理论的承载力值，当b=1，c在0～1之间取值时，则本理论的承载力值均大于双剪统一强度理论的承载力值，由此表明：极限承载力在较大程度上也受到系数c的影响，且随着c值的增加而增大.

(2)当基础底部处于完全光滑状态时，系数b与c分别在0～1之间取值，最终解得相应的极限承载力值，如表4所示，并绘制了此条件下系数b、c与qu之间的关系图，如图6所示.

表4 完全光滑基底条件下的地基承载力值

图6 完全光滑基底条件下系数b、c与qu之间的关系图Fig.6 Correlation graphs between b, c andqu on completely smooth base

从表4及图6中也可以看出地基极限承载力qu受到b、c取值的影响，b、c取值越大，则qu越大.由表4的计算结果与3.1.2的结果相比可知，本理论的承载力值均大于经典太沙基承载力值；与3.2.2的结果相比可知，当b=1，c在0～1之间取值时，本理论的承载力值均大于双剪强度理论的承载力值；与3.3.2相比，当c=0，b在0～1之间取值时，式(1)蜕化成双剪统一强度理论，本理论的承载力值即为双剪统一强度理论的承载力值，当b=1，c在0～1之间取值时，则本理论的承载力值均大于双剪统一强度理论的承载力值，由此表明：极限承载力在较大程度上也受到系数c的影响，且随着c值的增加而增大.

4 结论

(1)本文推导出了太沙基地基极限承载力的三剪统一强度理论解，并可根据系数b、c的不同取值，将此理论解简化为其他不同的理论解.若b和c值均为0，则简化为Mohr—Coulomb理论解；若b不为0，而c值为0，则简化为双剪统一强度理论解.

(2)本文公式分别包含了以经典太沙基、双剪强度理论及双剪统一强度理论为依据的地基承载力公式，并与前三种理论解进行了对比分析表明：三剪统一强度理论解更加全面的考虑了材料中三个主剪应力的影响，将其潜能发挥的更大，既克服了传统太沙基公式保守的缺点，又将双剪统一强度理论中忽略的最小主剪应力考虑进来.

(3)随着系数b、c值的增加，由本文推导的三剪应力地基承载力值也在提高.三剪统一强度理论解适用范围很广，适用于许多不同类型地基的承载力计算，通过合理地确定b、c值从而得到更为真实的结果.