可变速机组无位置传感器控制技术研究
2019-06-13常鹏飞周百灵
田 炜,常鹏飞,周百灵
(国电南瑞科技股份有限公司,江苏省南京市 211103)
0 引言
可变速抽水蓄能机组采用的矢量控制策略需检测转子位置,常规的转子位置检测方法是安装光电编码器,但安装在抽蓄机组中的编码器易损坏[1],且安装难度较大,后期维护成本高,还存在同心度的问题,从而导致检测位置与实际位置不一致。
因此,采用无位置传感器的控制方法受到重视:基于控制对象数学模型的直接计算方法[2-3],但其数学模型对参数有依赖性,位置估计精度不高;有基于电机结构的不对称性的电感变换方法和高频注入方法[4-5],但在极对数较多、表面贴式的工程电机应用时,会由于凸极效应较弱而失效;有基于状态观测器的位置估计方法[6],通过重构被观测对象的状态空间模型,消除误差,对参数变化的鲁棒性较好。其中,扩展卡尔曼滤波法和模型参考自适应法属于状态观测器法。
本文通过构建可变速抽蓄机组的无位置传感器状态空间模型,分别设计了扩展卡尔曼滤波器和改进模型参考自适应,通过比较两种估计方法的位置和速度观测效果,通过仿真验证了两种方法的有效性。
1 无传感器控制方法
对于可变速机组而言,其高阶、强耦合、非线性的特点是无法直接应用KF法的,这里便需要引入扩展卡尔曼滤波器法来解决这一问题,这里将可变速机组的模型抽象并重新描述成EKF问题见式(1):

式中t——连续时间。
式(1)的系统噪声和测量噪声同样满足白噪声的条件。
区别于KF法的是,EKF法需要将非线性的问题线性化,采取的是在y=0点处泰勒展开的方法,这里将状态方程和输出方程的两个函数进行泰勒展开,得到式(2):
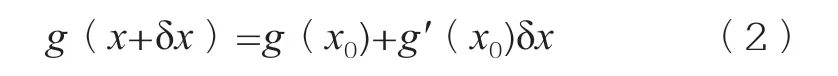
其中g′(x0)是一个n×n维方阵,常常称为雅各比方阵,其i,j分量见式(3)~(4)
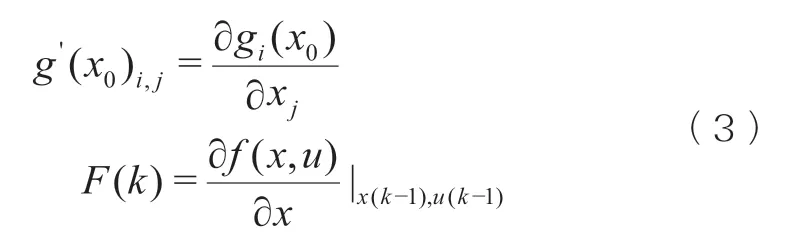
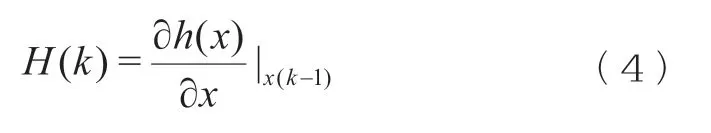
对应的扩展卡尔曼“黄金公式”见式(5):
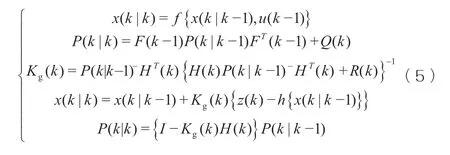
式中x——状态变量;
P、Q——惩罚矩阵。
和卡尔曼滤波器类似,模型参考自适应需要比较可调模型与参考模型的差值v,通过使二者的差值收敛至0,那么可调模型的状态估计值ˆx就等于参考模型的状态值x,进而得到系统的真实状态值。
不同的理论模型适用于不同的控制环境以及控制目的要求。事实上,根据选用的模型不同,可以有不同的自适应律,本文这里是基于转子磁链的MRAS控制器的设计方法。
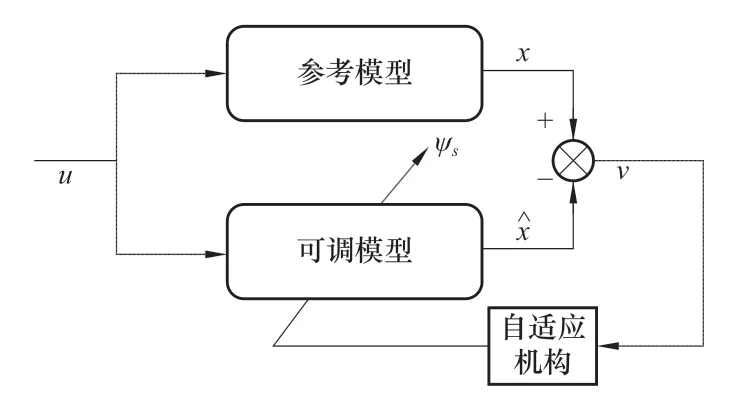
图1 MRAS结构图Figure 1 Diagram of MRAS
2 扩展卡尔曼滤波法设计
首先,写出可变速机组的状态空间方程,见式(6):
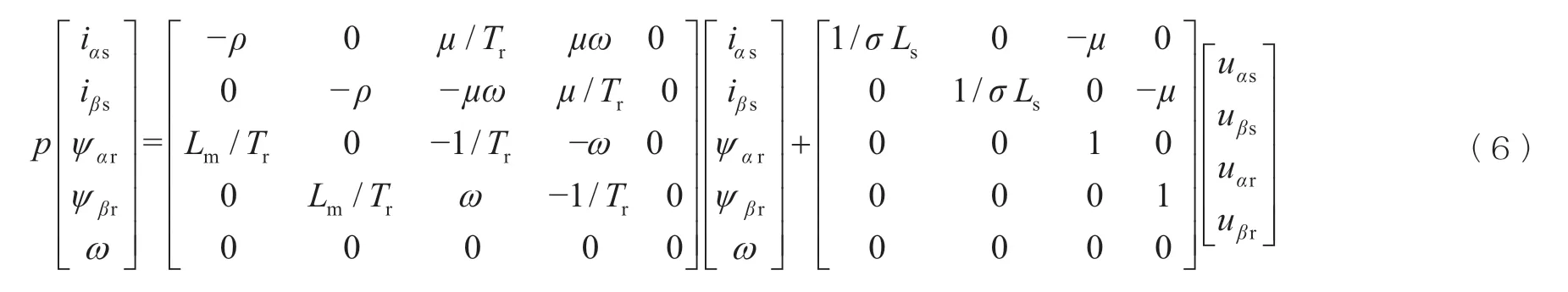
式中iαs/iβs——定子侧电流在α/β上的分量;
ψαr/ψβr——转子侧电流在α/β上的分量;
uαs/uβs——定子侧电压在α/β上的分量;
uαr/uβr——转子侧电压在α/β上的分量;
ω——转速,
Tr——转子转矩;
Ls——定子电感。
输出方程见式(7):
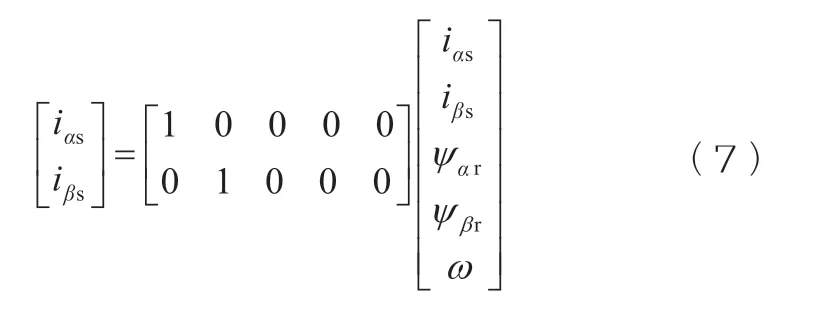
离散化方程(7),按照式(8):
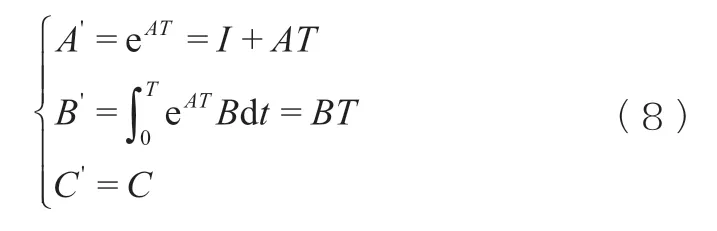
得到离散化后方程:

则得到式(9):
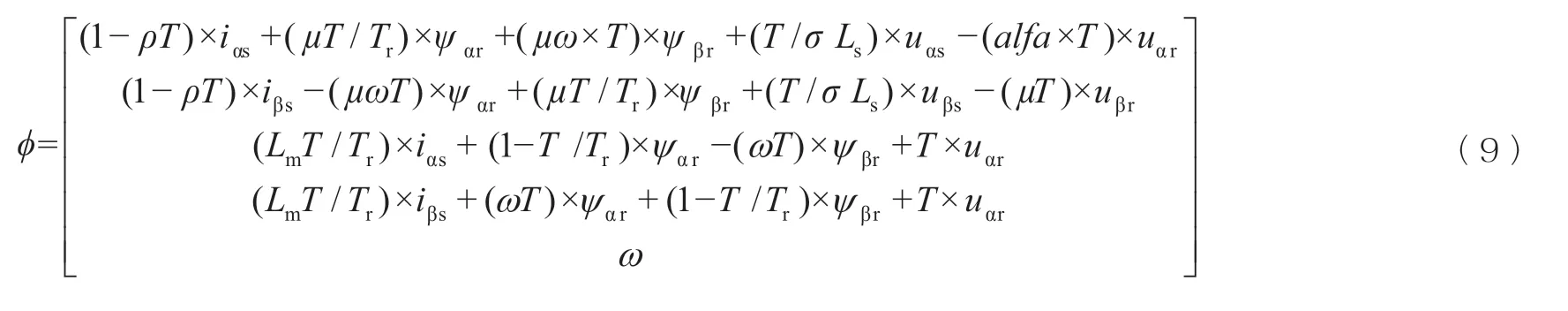

将Φ和h对x求导,得式(11)
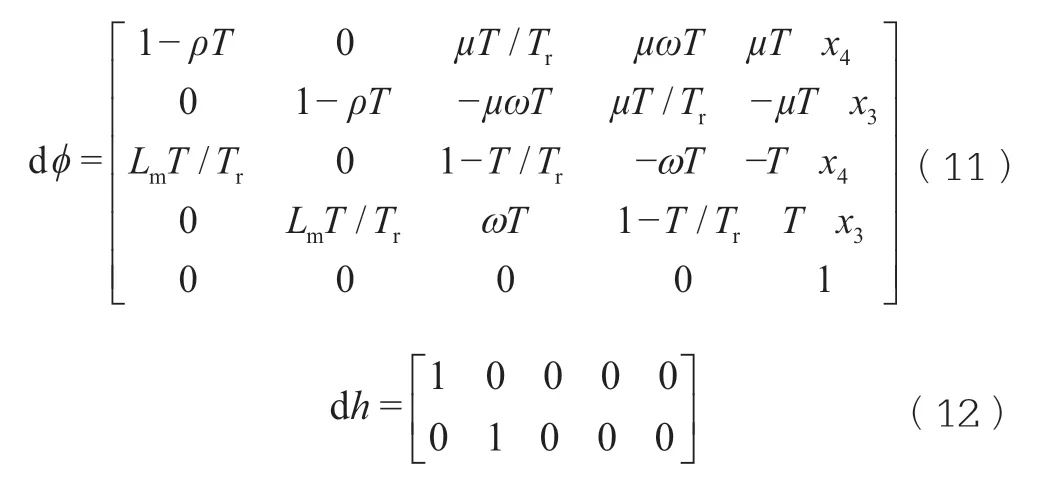
将上述方程代入黄金公式中去。
3 改进模型参考自适应设计
3.1 确定模型
和EKF法不同的是,MRAS法的模型方程不需要太复杂的推导,但是需要选择相同的状态量的不同参数模型,参考模型中不含待估计参数,而可调模型中包括待估计参数,两者的状态输出量差值,作为自适应机构的输入。根据可变速机组在两相静止坐标系中的数学模型,写出变换后的电压和磁链方程,构造转子磁链的电压和电流模型:
电压模型:
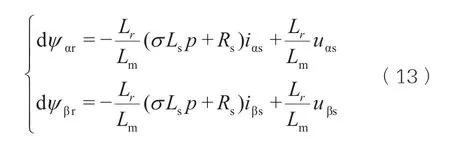
电流模型:
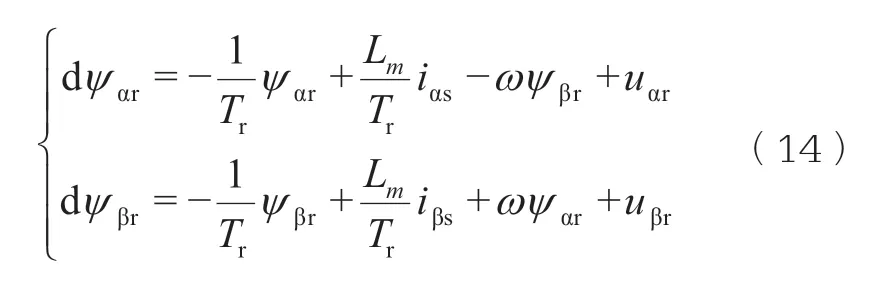
观察电压方程不含有待估计量转子转速ω,因而电压模型作为参考模型,而电流模型中含有变量ω,因而电流模型被确定为可调模型。
3.2 确定自适应律
文献[7]中已经通过对该模型满足波波夫超稳定要求的理论推导,这里不再赘述,直接给出基于转子磁链的模型参考自适应律如式(15)所示:

显然,转速的估计量结果是通过对转子磁链的参考模型输出值和可调模型的输出值行叉乘,再进行PI控制得到,这一结论和大多数MRAS法相一致。
3.3 系统框图
根据上述两个步骤,这里给出基于转子磁链MRAS法的系统框图如图2所示。
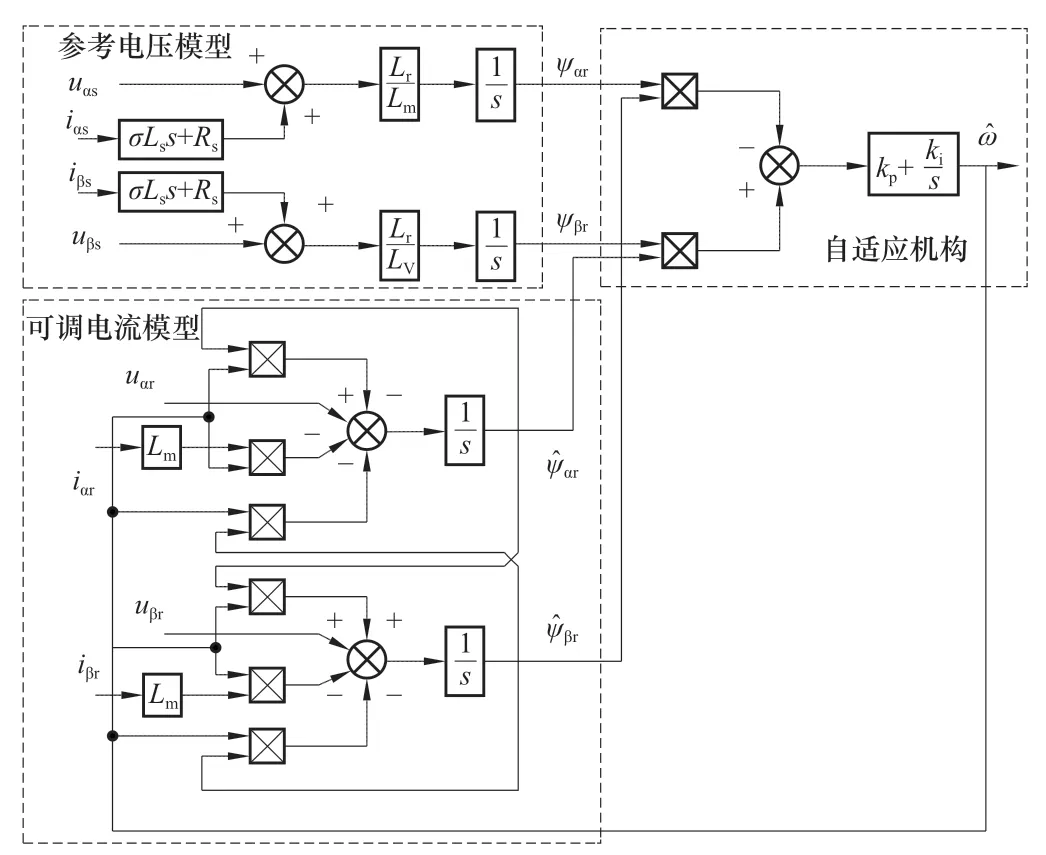
图2 基于转子磁链MRAS法控制系统框图Figure 2 Control block diagram based on MRAS of rotor flux
同样的,在离散控制器中,MRAS法存在微分环节σsLs和纯积分环节,因此便存在噪声放大和积分饱和的问题,因此,本文采用一种改进的MRAS法,改写式(13)为式(16):
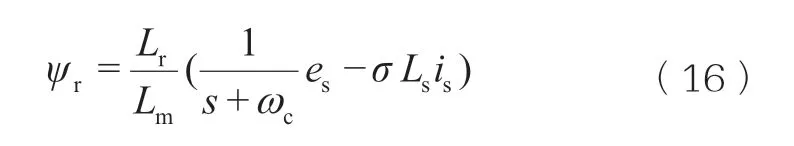
如图所示,将积分环节用一阶惯性环节替代,并且采用对定子磁链限幅补偿的方式,得到如图3所示的模型参考自适应的改进电压模型。
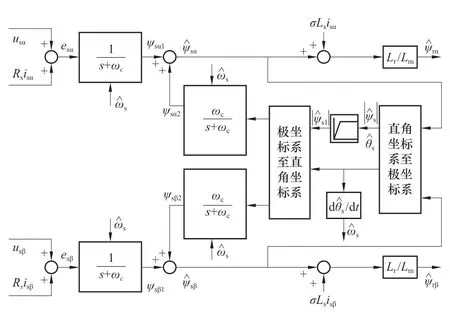
图3 改进电压参考模型Figure 3 Model of improved voltage reference
4 仿真验证
为了比较分析3.2小节中的EKF法和MRAS法的转子位置估计精度和参数发生变化下的鲁棒性,这里对如表1所示电机参数的可变速机组进行Simulink仿真验证。

表1 电机参数Table 1 Motor parameters
本文分别给出两种方法在空载和加载情形下的转速和位置估计效果,并分别给出1000r/min和750r/min两种转速条件下的估计效果,研究定子电感偏差下的估计效果。
根据机组的极对数,额定转速为1500r/min,因此为了分析不同转速下的位置跟踪效果,分别给出:1000r/min和750r/min转速下,两种方法的估计结果。

图4 1000r/min下EKF法和MRAS法转子位置估计值Figure 4 Rotor position of EKF method and MRAS method under 1000r/min
根据图4,在1000r/min转速下,图4(a)为EKF法转子位置估计值与实际值仿真结果图,图4(b)为MRAS法转子位置估计值与实际值仿真结果图,对比发现,两种方法的转子位置估计值都能够在第三个周期以后跟踪实际值。
图5所示为1000r/min转速下,两种方法的位置估计误差,图(b)MRAS法的误差超调量(-1.1rad)显著大于图(a)EKF法的误差超调量(0.43rad)。两者的稳态估计误差均在0.02以内,但MRAS法估计误差在0.15~0.18s以后进入稳态,而EKF法则在0.25s后进入稳态。
从图6中可以看出,两种方法的转速给定为1000r/min,观察二者发现,MRAS法相较于EKF法对转速的估计,前者的响应速度更快,但超调更大,而且0.5s之前的估计值稳态误差也更大,但两者对于速度的跟踪都能保持良好的估计效果。
图7所示为转速估计值与实际值的误差曲线,可以定量的看出,EKF法的转速超调不超过100r/min,而MRAS法的转速超调最大为-600r/min,换言之,机组在起动的过程中有一个短暂的反转过程,然后才能进入正常起动状态;在进入稳态以后,EKF法的转速估计误差在-10~10r/min范围内,而MRAS法在0.5s之前的转速误差波动范围达到-200~200r/min,0.5s以后其误差绝对值也在20r/min附近。
图4~图8的估计结果均是在可变速机组空载的情况下仿真得到的,为了进一步比较两者在加载以后的动态跟踪效果,接下来进行0.5s加载的仿真对比,并进一步比较750r/min下加载的稳态和动态性能。

图5 1000r/min下EKF法和MRAS法转子位置估计误差Figure 5 Rotor position error of EKF method and MRAS method under 1000r/min

图6 1000r/min下EKF法和MRAS法转速估计值Figure 6 Rotor speed of EKF method and MRAS method under 1000r/min
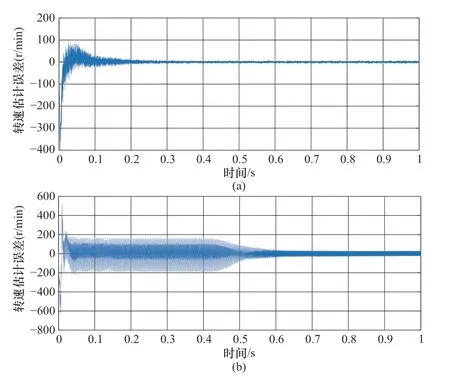
图7 1000r/min下EKF法和MRAS法转速估计误差Figure 7 Rotor speed error of EKF method and MRAS method under 1000r/min

图8 1000r/min下EKF法0.5s加载估计误差Figure 8 Loading estimation error of EKF method under 1000r/min when 0.5s
首先在1000r/min仿真运行至0.5s,进行加载,如图9所示,为EKF法加载后的转速估计误差和位置估计误差,可以发现,转速估计误差在加载瞬间发生超调突变(30r/min以内),但在经过0.02s后又能恢复稳态;观察位置估计误差发现,其误差值大小同样会在加载瞬间突变,但经过0.05s后恢复稳态,但稳态误差值相较于空载情况下增大,但依然在0.05rad以内。
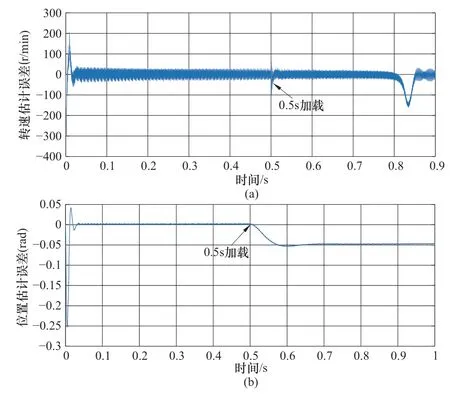
图9 1000r/min下MRAS法0.5s加载估计误差Figure 9 Loading estimation error of MRAS method under 1000r/min when 0.5s
如图9所示为MRAS法在0.5s加载前后的转速和位置估计误差曲线,转速估计误差在加载瞬间的超调量达到了-150r/min,在0.01s后迅速恢复,但此时的转速已经不稳定,在0.84s左右出现误差抖动增大的情况;同样的,位置估计误差在加载以后同样出现了偏差增大的问题。
进一步地,如图10所示,在750r/min仿真运行下,进行0.5s加载验证,对于EKF法转速估计误差结果,其起动转速误差超调缩小至-400r/min以内,但0.5s加载后的转速估计误差超调增加,恢复时间也增长至0.04s;同样的,EKF法的位置估计误差在起动阶段的超调量也下降至0.5rad,但加载瞬间的误差超调量也明显增加,并且恢复后的稳态误差也大于加载前,这与1000r/min下的结论是一致的。
在图11中,对于MRAS法转速估计误差结果,在750r/min仿真条件下,最显著的特点是其转速估计误差绝对值从原来的200r/min降到了40r/min,起动转速超调量也显著下降,说明MRAS法对于低稳态转速的估计效果更为良好。但带来的问题也是不可忽视的,在0.5s加载瞬间,其转速估计误差超调至-430r/min,远远大于1000r/min下的-150r/min的加载超调量,并且加载以后的转速误差在0.69s附近发生抖动,说明加载后的转速估计效果下降。而对于MRAS法位置估计误差结果,750r/min运行下的位置误差调节时间也显著增加,而且加载后的稳态误差也显著增加。
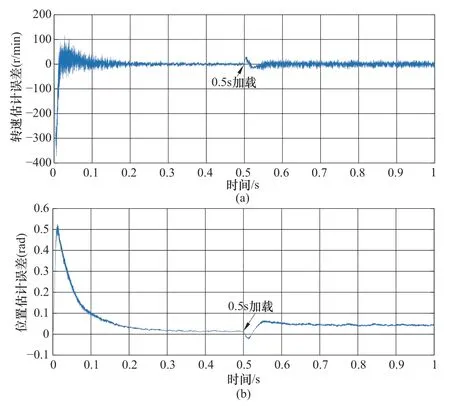
图10 750r/min下EKF法0.5s加载估计误差Figure 10 Loading estimation error of EKF method under 750r/min when 0.5s
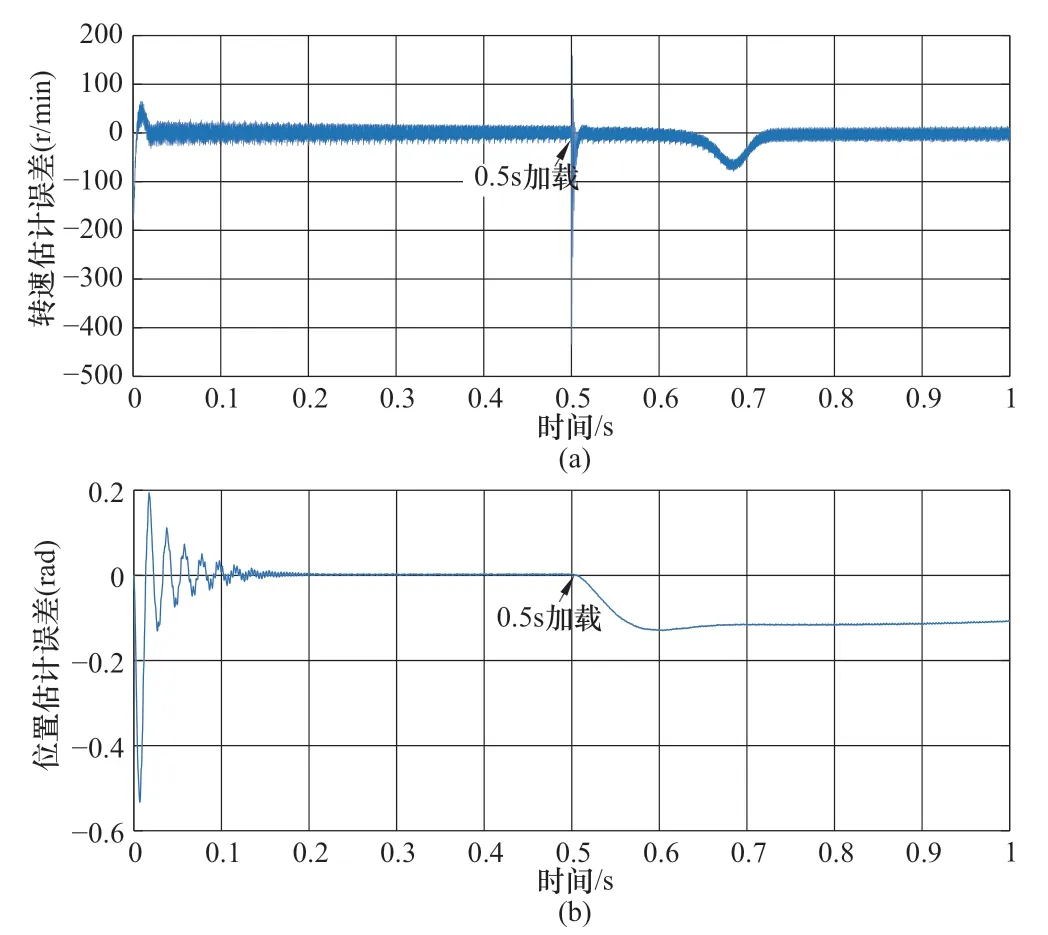
图11 750r/min下MRAS法0.5s加载估计误差Figure 11 Loading estimation error of MRAS method under 750r/min when 0.5s
综上所述,EKF法和MRAS法仿真比较发现,无论是在空载情况下还是加载以后,对于转速估计精度而言,EKF法是显著优于MRAS法的,并且EKF法对于突变负载的鲁棒性更好;对比两种方法在1000r/min和750r/min下的仿真结果,虽然MRAS法在750r/min下的转速估计误差结果同样理想,但其加载以后的超调量和稳态误差偏大,其位置估计误差也存在同样的问题。
5 结束语
通过对可变速抽蓄机组的建模,研究了扩展卡尔曼滤波和改进MRAS两种无传感器转子位置辨识方法,并分别对两种方法进行观测器设计。其中,针对常规MRAS法存在微分环节和积分偏差问题,针对电压参考模型进行了改进。通过仿真比较两种方法在不同转速以及加载前后的转子位置和转速观测效果,得出扩展卡尔曼方法效果更佳的结论。
