基于多工况ANFIS模型的高速动车组运行速度控制
2019-06-13付雅婷
付雅婷,杨 辉
(1. 华东交通大学 电气与自动化工程学院,江西 南昌 330013;2. 华东交通大学 江西省先进控制与优化重点实验室,江西 南昌 330013)
高速动车组是一个由多个工况组成的具有非线性和时变性的复杂系统。对其运行过程进行准确控制是提高运行性能的重要手段之一。现有的高速动车组运行控制主要是基于ATP(列车自动防护系统)的人工操作模式,由于高速动车组运行过程需在牵引、制动和惰行工况中多次切换,动车组的运行性能依赖驾驶员的操作技术,容易引起不可预期的速度波动。因此,针对高速动车组运行特性,建立有效的高速动车组运行过程模型和设计有效的运行控制方法已成为高铁自动驾驶系统的发展趋势[1-3]。
对于高速动车组运行过程的建模,传统的建模方法主要采用机理建模[4-5],其模型的单一性,模型参数的不变性在很大程度上满足不了描述高速动车组运行动态的要求。数据驱动建模是利用数据挖掘技术寻找数据之间的有用信息,建立更具体、更明确的函数表达形式来描述输入与输出之间的关系。采用数据驱动建模方法可在很大程度上克服机理模型的不足。文献[6] 针对高速动车组的结构特点,建立一种数据驱动子空间预报模型,但其模型表达缺乏具体的物理意义,不利于模型参数的调整。文献[7]基于多模型切换方法建立了高速动车组数据驱动多模型预测控制方法,但模型之间如何平稳切换还没有很好的办法。
针对列车运行速度控制,较经典的是PID控制方法[8],由于PID控制自适应能力的局限,其比较适用于环境较稳定、速度较低的城市轨道交通系统。为了解决这个问题,目前较为常用有效的是自适应容错控制和广义预测控制。文献[9]采用自适应容错控制方法实现高速动车组速度、位置跟踪控制,提高系统性能指标。文献[10]针对高速动车组的多动力单元组成特点,提出一种分布式自适应容错控制方法来完成高速动车组的牵引和制动控制。广义预测控制方法具有反馈校正和滚动优化的优点,可以有效克服过程的不确定性和非线性,适用于高速动车组这样的复杂不确定系统。文献[7,11]提出高速动车组广义预测控制,实现了高速动车组运行过程速度、位移的高精度控制。但上述控制方法均没有考虑动车组多工况运行的特点,其对处理实际高速动车组运行问题的能力还需提高。
针对高速动车组运行过程具有高度不确定性和较强的非线性,本文采用结合了人工神经网络和模糊推理系统优良特性的自适应模糊推理系统(ANFIS)[12]建模方法对高速动车组运行过程进行描述。在文献[13-14]的基础上,建立高速动车组运行过程多工况ANFIS模型,为高速动车组运行控制提供有效基础。并基于多工况ANFIS模型设计相应预测控制器,控制高速动车组高精度跟踪目标曲线安全运行。
1 高速动车组动力学分析
图1为高速动车组运行受力情况。目前,高速动车组运行是通过驾驶员在HMI (车辆信息系统人机界面)和ATP显示屏的指导下操纵牵引/制动手柄获得控制力,从而完成牵引、制动、惰行工况之间的转换。
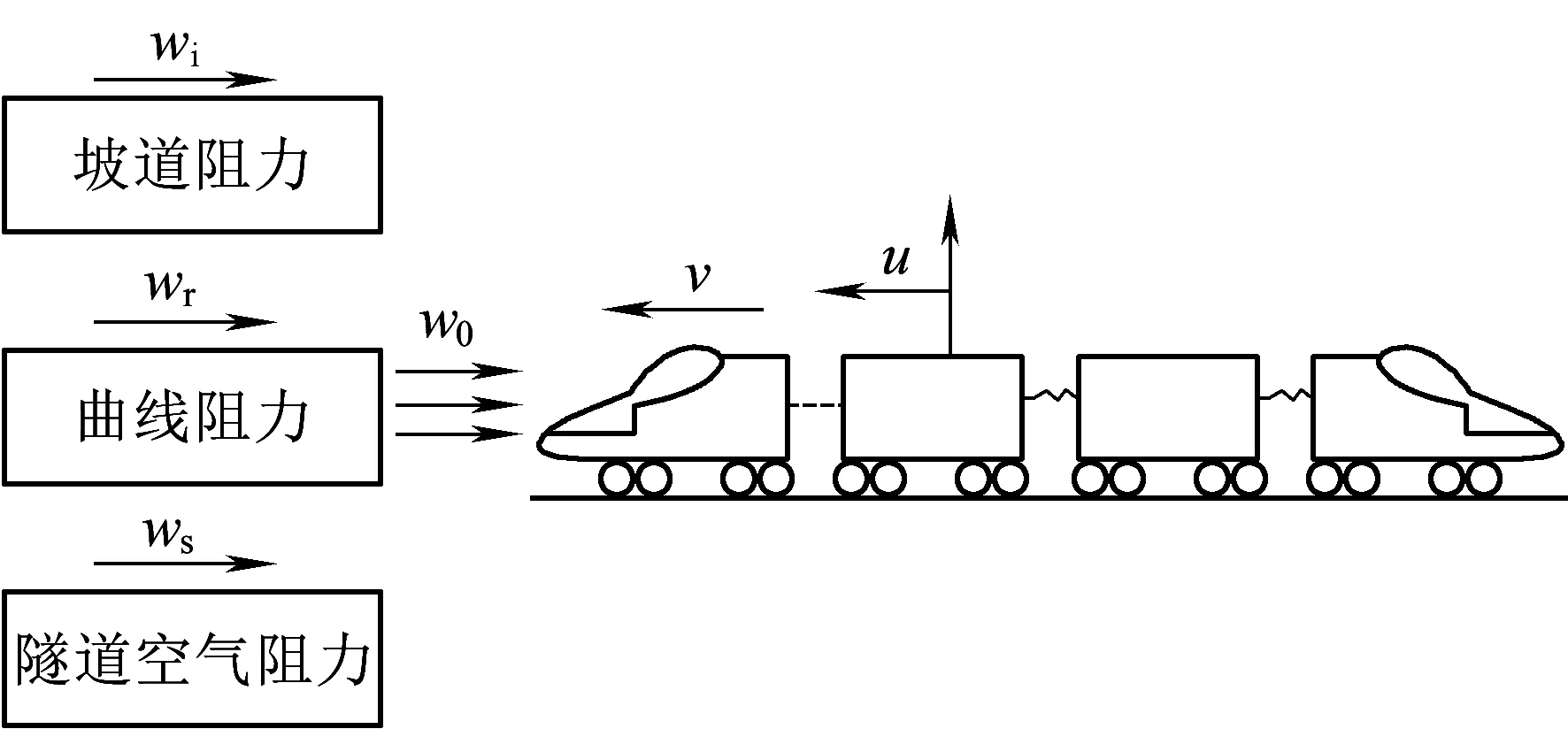
图1 高速动车组运行过程受力情况
由于高速动车组在运行过程中受到基本阻力和附加阻力的作用,其运动过程受力情况可表示为
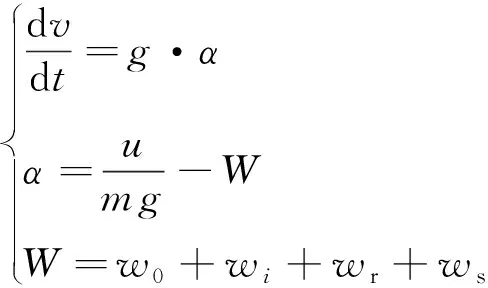
( 1 )
式中:v为高速动车组运行速度变量,通过测速测距单元获得;g为重力加速度;u为控制力变量;α为作用于高速列车上的单位合力;单位阻力W由单位基本阻力w0和单位附加阻力组成[15]。列车运行中的w0由多方面因素组成,有各种冲击和振动阻力以及空气阻力,在实际运用中难以用理论公式来表达。因此,通常使用大量试验综合得出的经验公式作为计算公式,这些公式一般是运用动车组运行速度的一元二次方程的表现形式。单位附加阻力由单位坡道阻力wi、单位曲线阻力wr和单位隧道空气阻力ws组成。我国单位坡道阻力在数值上等于该坡道的坡度千分数;单位曲线阻力和单位隧道空气阻力通常采用机理分析加试验得出的经验公式。通常,高速动车组的单位基本阻力和单位附加阻力可以表示为
( 2 )
式中:η1,η2,η3为基本阻力系数;η3v2为正常情况下的空气阻力;iw为坡度千分数;αw为曲线中心角;Lr为曲线长度;Ls为隧道长度。这些公式和参数均由机理分析和试验获得。
不同工况作用于高速动车组上的单位合力可以表示为
牵引工况:
制动工况:
惰行工况:
α=-W=f2(v)u=0
高速动车组的恒速模式包含以上三种工况(例如:平直线路上是牵引工况,下坡线路是惰行或者制动工况)。F为操纵牵引手柄获得的牵引力,B为操纵制动手柄获得的制动力。
将式( 2 )代入式( 1 ),可以得到高速动车组运行过程动力学模型为
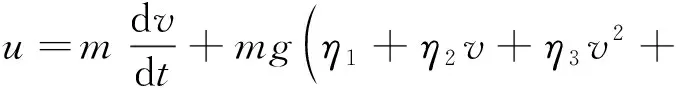
( 3 )
2 高速动车组多工况ANFIS模型
ANFIS建模算法是通过给定的输入输出数据集构建一个模糊推理系统,采用减法聚类方法将系统分为合适的模糊规则,获得相应隶属度参数即前件参数,并利用最小方差算法计算后件参数。对所有规则进行整合,获得一个ANFIS模型。最后,根据建模数据采用反向传播梯度下降法对其前件参数和后件参数进行优化调整,使前、后件参数更加适应输入输出数据[16]。所以,ANFIS算法是一种既可表达模糊语言变量又具有学习功能的建模控制方法。本文对高速动车组的牵引、制动和惰行工况分别采用ANFIS建模方法,建立多工况ANFIS模型。
2.1 多工况ANFIS模型规则划分
对高速动车组运行数据进行预处理,根据控制力的大小将运行数据划分为牵引、制动和惰行3个工况数据。但用多少条模糊规则来表述规则所在的有效工况成为首先要解决的问题。因此,针对每个运行工况数据,分别采用减法聚类方法将高速动车组不同运行工况数据进行划分。减法聚类算法将每个数据点作为可能的聚类中心,并根据各个数据点周围的数据点密度计算该点作为聚类中心的可能性,能够充分利用数据的内部特征对系统进行分类,是复杂系统分类的热门方法[17]。
以牵引工况为例,假设牵引工况有m个高速动车组运行过程数据点{X1,…,Xi,…,Xm},其中Xi=[vi(k-1)ui(k-1)vi(k)],数据点Xi处的密度指标定义为

( 4 )
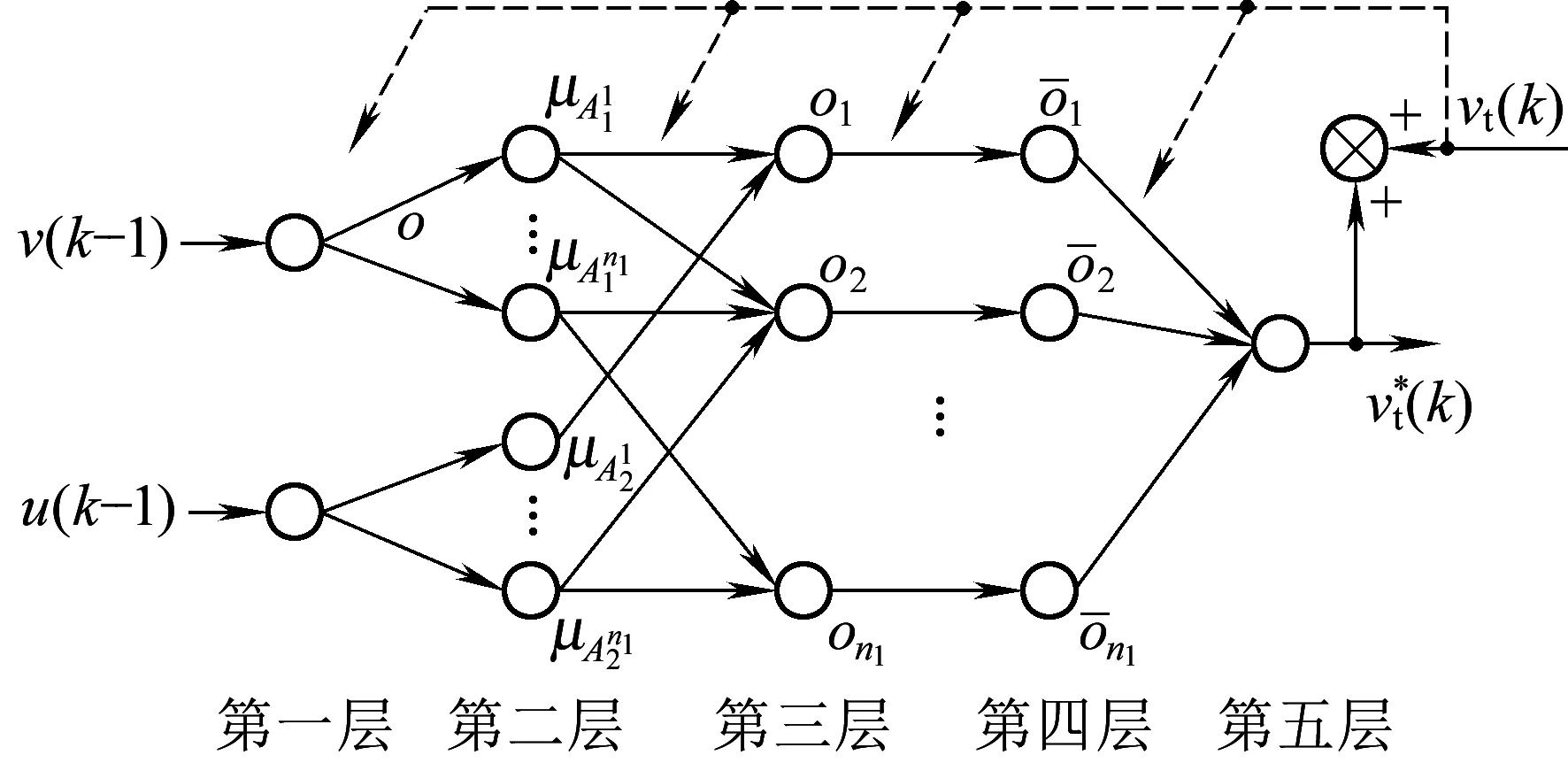
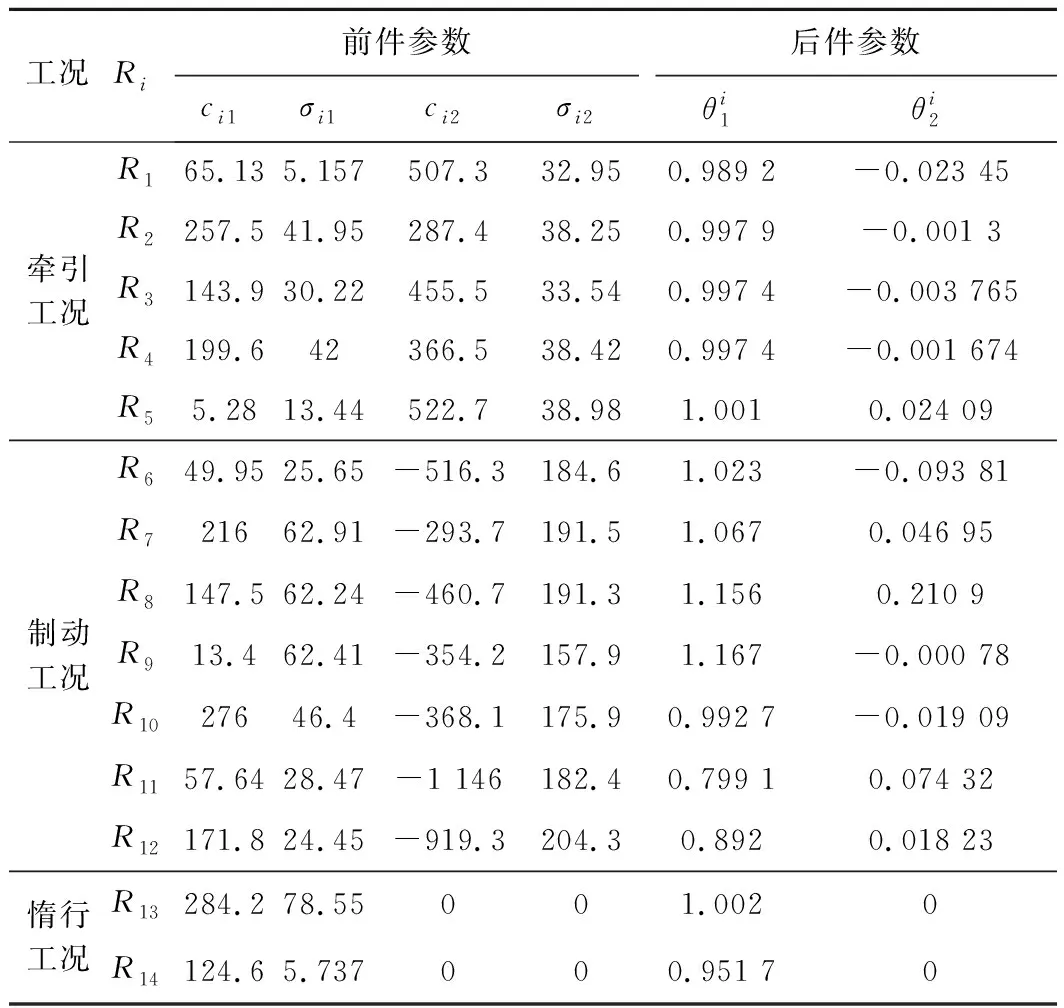
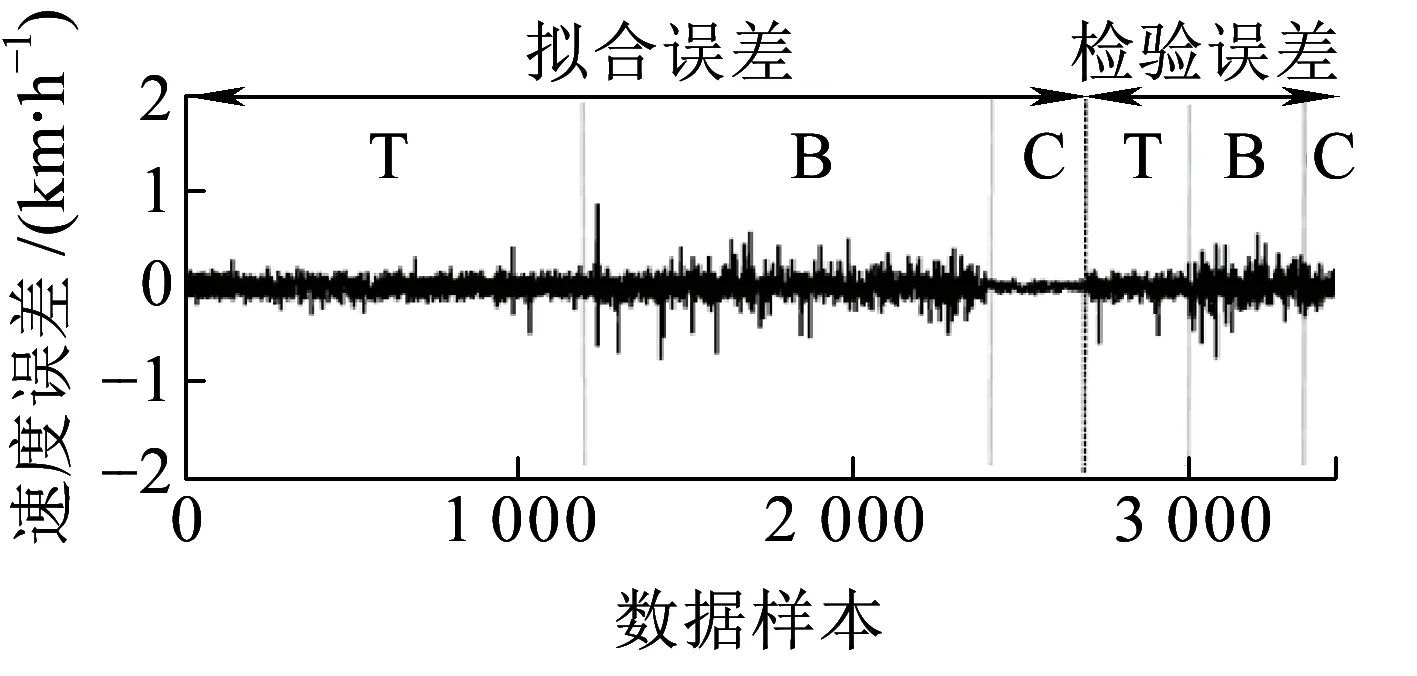
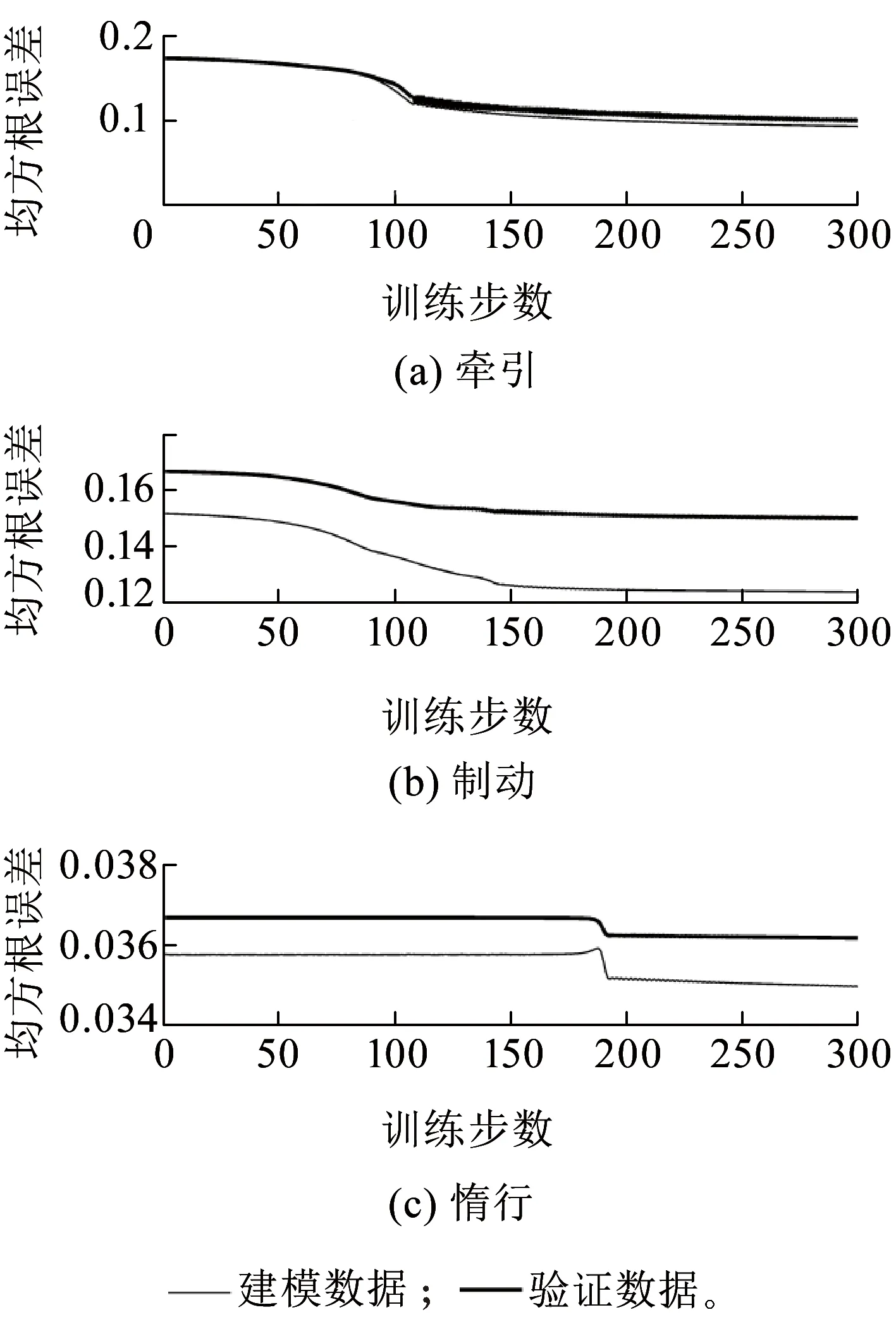
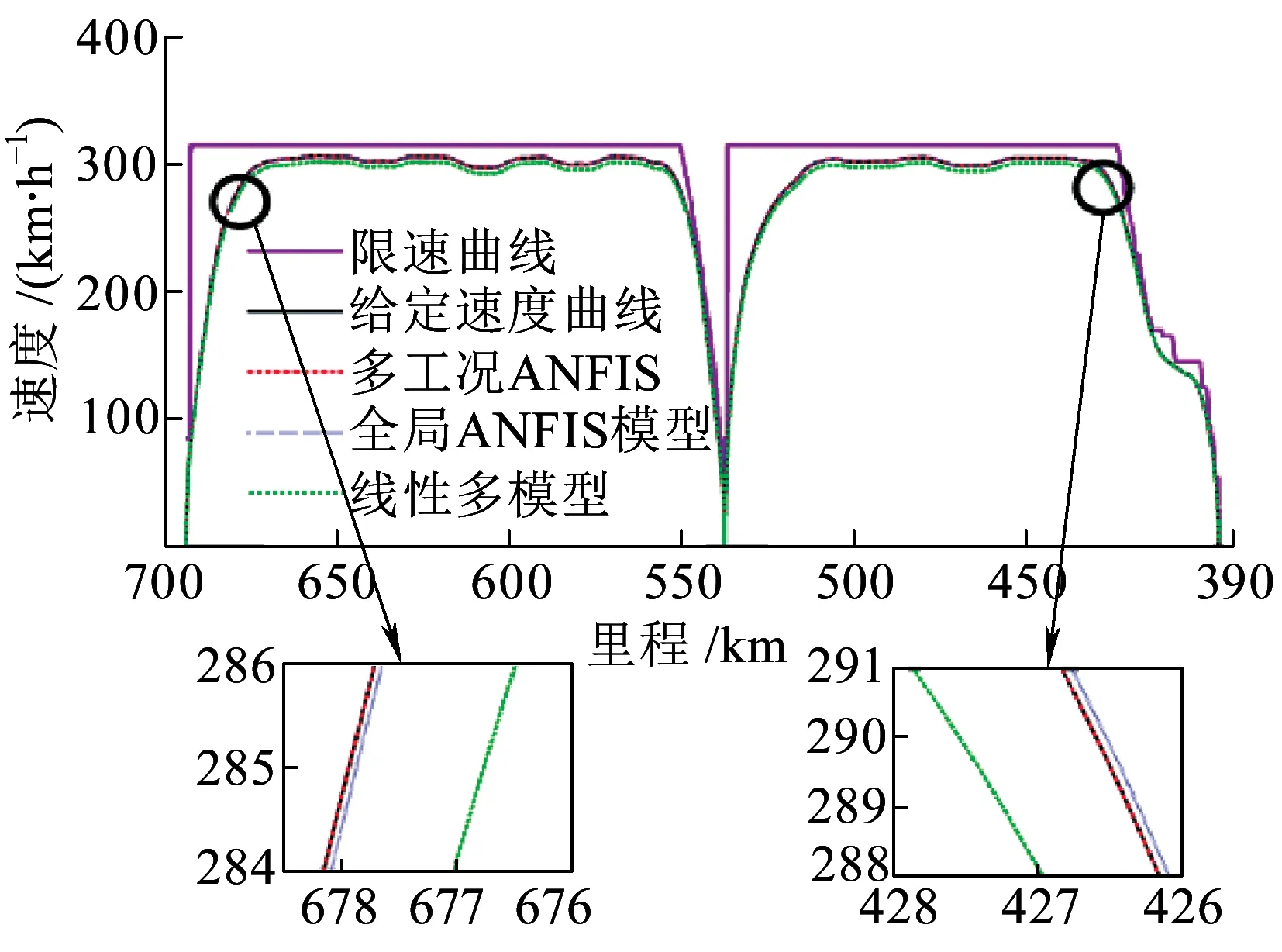
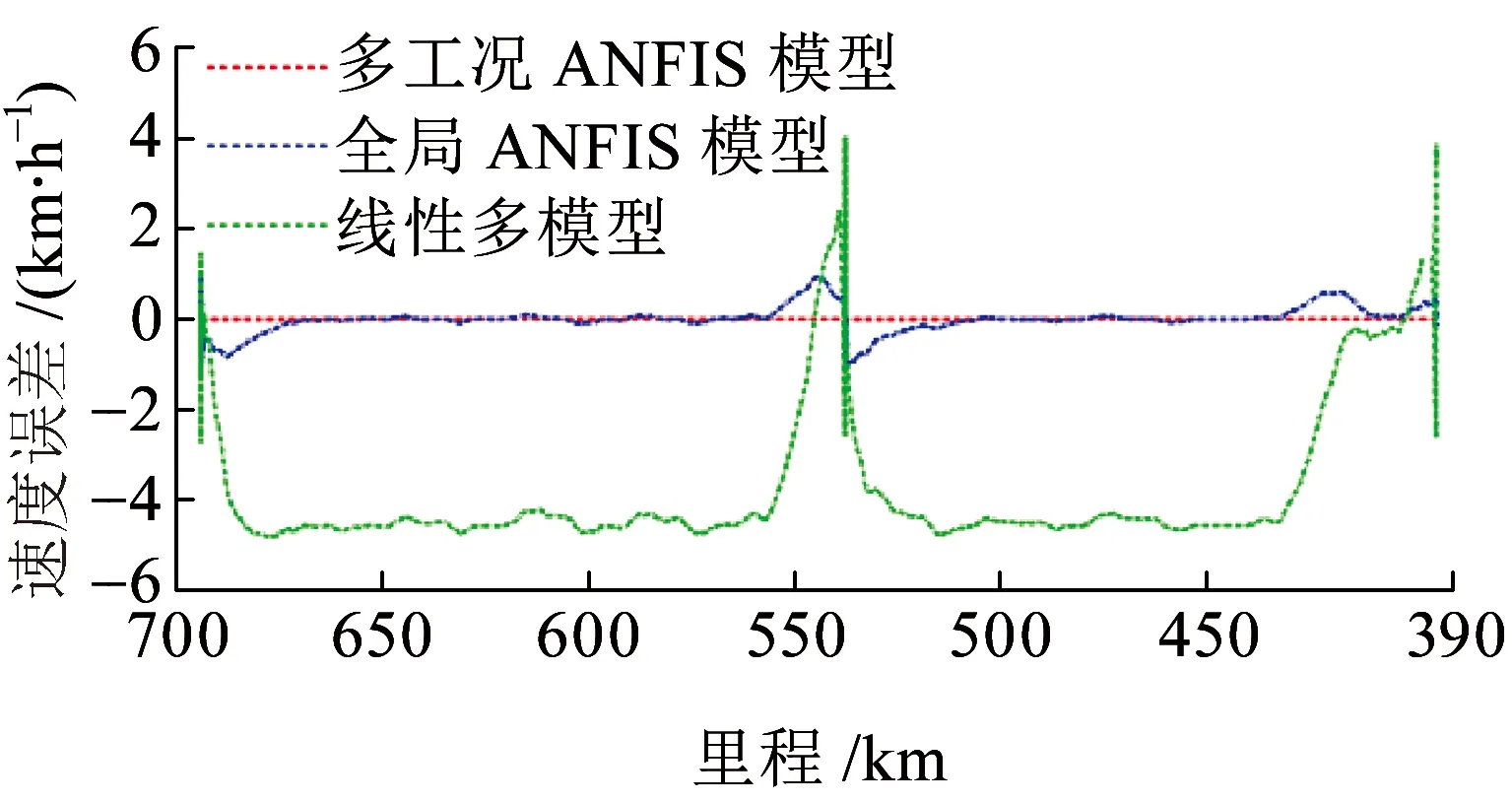
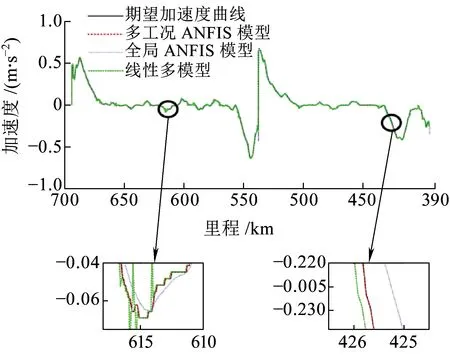
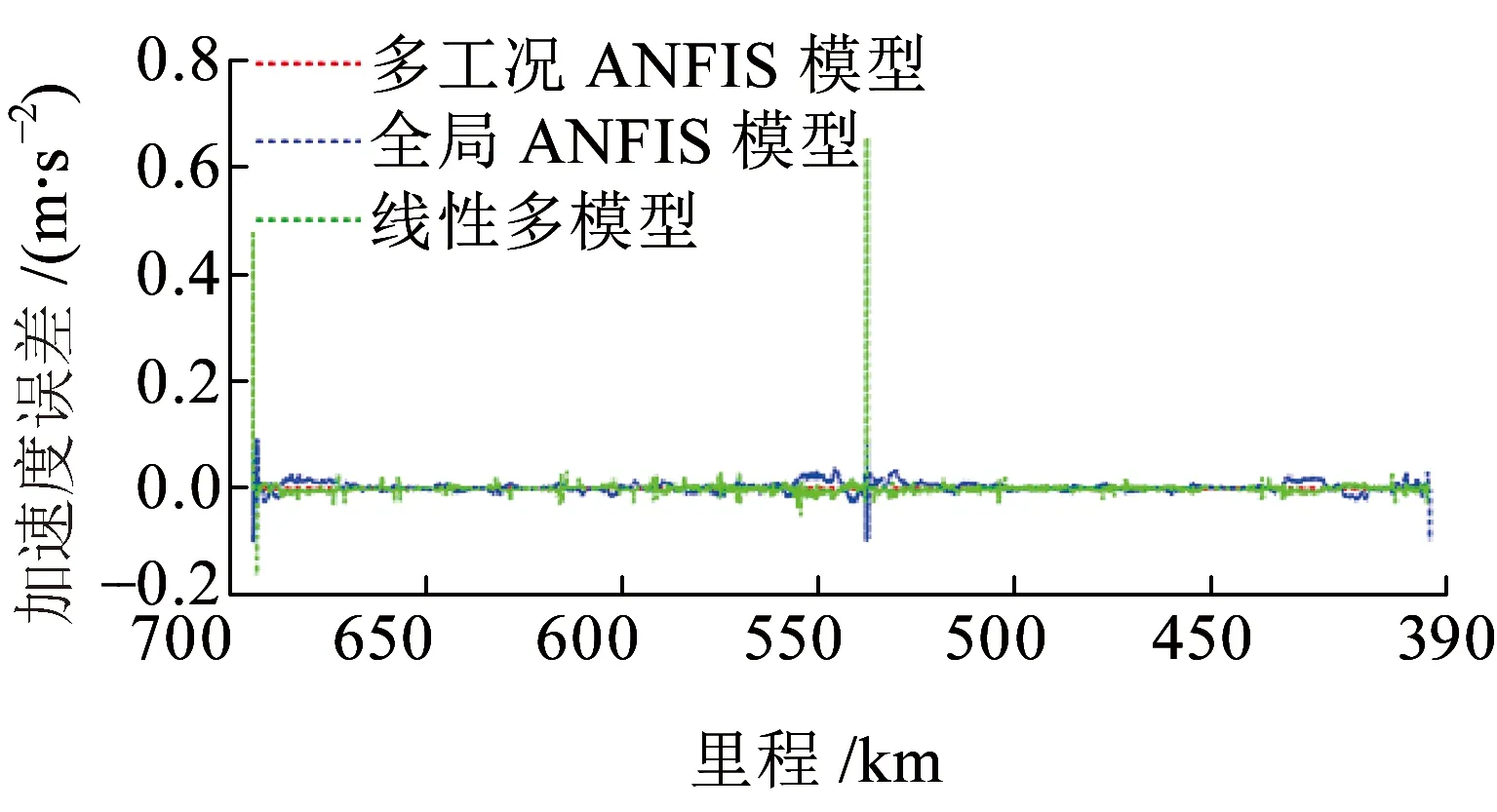
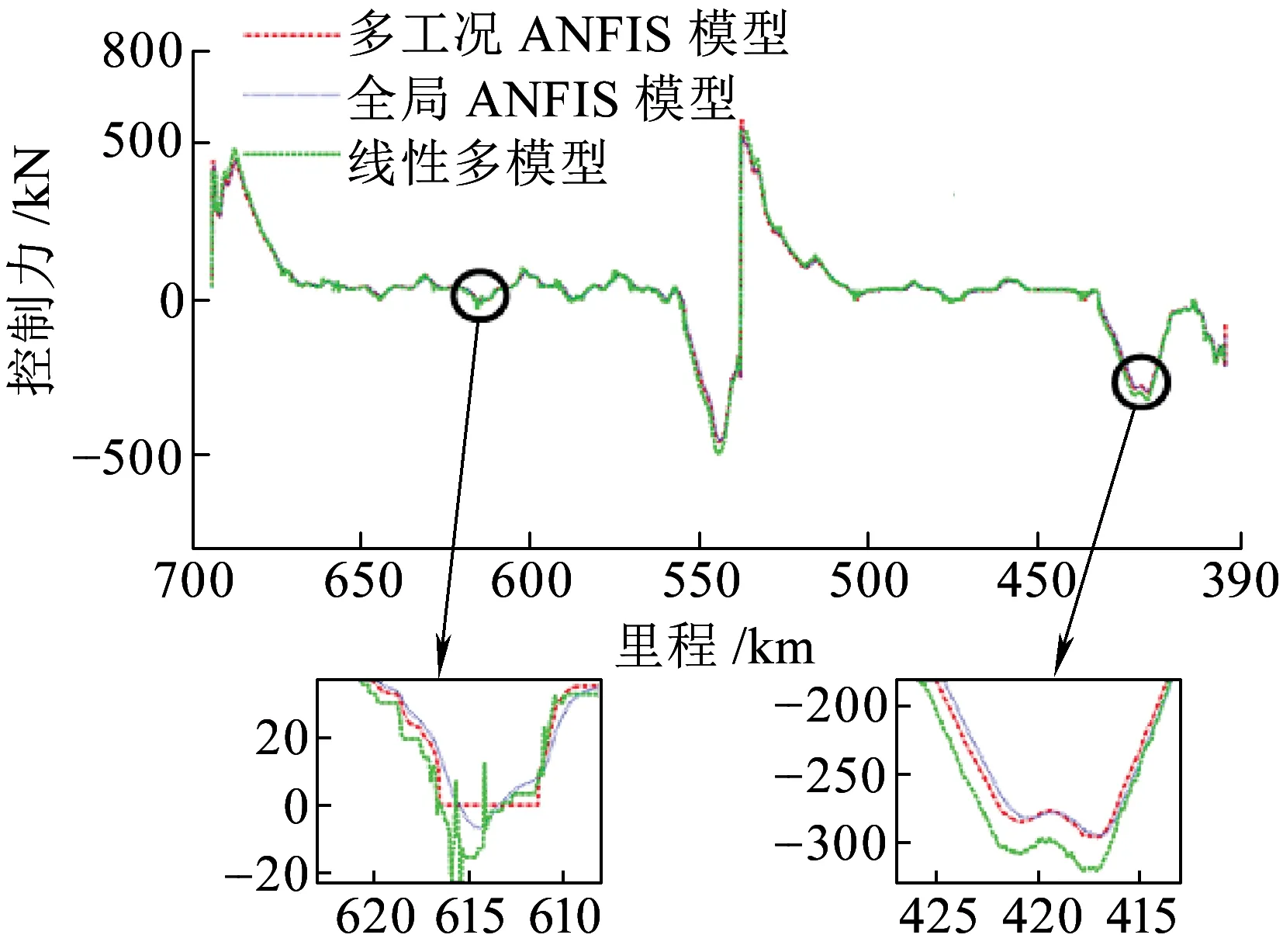
式中:δa为设定的聚类中心有效邻域半径,是一个正数。选择密度指标最高值Dc1=maxDi得到第一个聚类中心c1=Xi|maxDi,余类推,再采用Davies-Bouldin (DB)聚类有效性指标确定最优聚类中心个数,具体参见文献[7]。采用减法聚类方法可获得牵引工况数据的聚类中心个数为n1,且n1 牵引ANFIS模型的第i条初始规则可表示为 ( 5 ) 计算输入变量v(k-1),u(k-1)满足规则Ri的程度可定义为 ( 6 ) 式中:χ1=v(k-1),χ2=u(k-1);前件参数(隶属度函数的中心和宽度)cij和σij对应于减法聚类的聚类中心和宽度。 每条规则的后件参数分别采用最小二乘法获得,其中第i条规则的后件参数可表示为 ( 7 ) 对n1条牵引ANFIS模型规则进行加权融合,可获得总的牵引ANFIS模型输出为 ( 8 ) 其中 ANFIS方法是将神经网络与模糊理论相结合,取长补短,利用神经网络来学习调整模糊推理系统的参数,使得所建ANFIS模型更逼近非线性系统。参数学习优化是通过结合反向传播方法和梯度下降方法来完成,牵引ANFIS模型神经网络结构图如图2所示。具体优化步骤为: 图2 高速动车组运行过程牵引ANFIS模型神经网络结构 ( 9 ) (10) (11) (12) (13) 步骤2 采用梯度下降法优化调整规则前件参数。 (14) 学习速率αc、ασ和αθ由实验获得。其余制动ANFIS模型和惰行ANFIS模型采用相同方法获得,在此不再赘述。 高速动车组运行环境复杂,影响运行性能的因素较多。对动车组进行运行控制需保障动车组平稳跟踪给定的目标设定速度vr运行。广义预测保留了自适应控制的优点且更具鲁棒性,采用多步预测、滚动优化更适用于复杂不确定系统[18]。基于上述建立的高速动车组多工况ANFIS模型,相应的广义预测控制器设计如下,采用一种选择机制选择最匹配的工况模型给广义预测控制器,并结合预测输出速度v和设定输出速度vr的误差,通过计算获得相应的控制力去执行高速动车组的运行控制。控制框图如图3所示。 图3 基于多ANFIS模型的预测控制器框图 采用以下性能指标函数计算最匹配模型的输出v*。令在k时刻,实际输出与各个工况ANFIS模型输出之间的误差为ei(k)=vr(k)-vi(k),(i=t,b,c)。定义切换性能指标[19]为 (15) 在每个采样时刻,计算各个工况模型的性能指标系统。式中参数c>0,d>0,分别为当前时刻和过去l个时刻失配误差的加权系数;遗忘因子0<ρ≤1,表示过去l个时刻的失配误差在系统性能指标中被遗忘的程度;l是过去时刻的时域长度。Ji越小表示模型失配也越小。通过式(15)性能指标的最小值,选择最匹配的工况ANFIS模型。 建模过程得到的高速动车组运行过程模型式( 8 )可以描述为受控自回归积分滑动平均过程模型(CARIMA)形式。 (16) 其中 Δ=1-z-1 为了获得控制律,需最小化性能指标函数[20]。 (17) 已知未来(t+j)时刻的期望输出vr(t+j),N0为最小输出时域,Nl为预测时域,Nu为控制时域。控制增量Δu(t+j-1)为自由变量,rj>0(j=1,…,Nu)表示控制量的加权系数。 为解决该问题,引入丢番图方程 (18) fj(z-1)=b(z-1)ej(z-1) (19) fj(z-1)=b(z-1)ej(z-1)=lj(z-1)+z-jhj(z-1) (20) 当最优实际预测估计输出 v*(t+j)=ljΔu(t+j-1)+hjΔu(t-1)+gjv(t) (21) 时,性能指标函数J取得最小值。 将式(17)写成矩阵形式 (22) 最优预测估计输出可以表示为 V*(t+j)=LΔU(t+j-1)+ (23) ΔU(t+j-1)=(LTQL+R)-1LTQ[Vr(t+j)- (24) 从而滚动优化可得到t时刻的控制力为 (25) 为了验证本文提出的高速动车组运行过程多工况ANFIS建模方法和运行控制方法的有效性,选用在国内使用较为广泛的CRH380AL型高速动车组为实验验证对象。采集该动车组在京沪高铁徐州东到济南西区段若干趟同一车次的全程运行速度、控制力数据,结合CRH380AL牵引和制动特性曲线,选择速度范围0~310 km/h,代表牵引、制动、惰行所有工况的3 550组有效数据,并全局平均取其中2 700组数据作为建模数据样本,剩余850组数据作为检验模型精度的数据。 将2 700组建模样本数据按牵引、制动、惰行工况分为1 200,1 200和300组。采用第3章的高速动车组运行过程多工况ANFIS建模方法对三种工况数据进行建模。采用减法聚类将三类数据分别进行划分,获得14条规则,其中5条牵引工况规则,7条制动工况规则和2条惰行工况规则,并获得每条规则的前件参数(隶属函数中心和宽度)。采用最小方差估计对规则后件参数进行辨识,获得规则后件参数。结合反向传播方法和梯度下降算法对多工况ANFIS模型前/后件参数进行优化调整。优化后的多工况ANFIS模型规则参数见表1。为验证所建多工况ANFIS模型的有效性,采用剩余850组运行数据对所建立的模型进行验证。模型输出误差分布如图4所示,3个工况的建模数据和检验数据的均方根误差在模型优化训练过程中的变化曲线如图5所示。 表1 多工况ANFIS模型规则参数 图4 多工况ANFIS模型的输出误差分布曲线(T:牵引,B:制动,C:惰行) 图5 多工况ANFIS模型建模数据和检验数据的均方根误差变化曲线 从图4我们可以观察到,多工况ANFIS模型3个工况下的拟合误差和检验误差范围分别为-0.767~0.914 8 km/h和-0.811 3~0.725 1 km/h,满足CTCS-3列控系统的定位测速要求。图5显示,通过优化训练,多工况ANFIS模型三类子模型的建模数据均方根误差和验证数据的均方根误差均有明显变小趋势,且在训练到200步左右的时候均达到最小,在200步以后,均方根误差变小的速度明显变慢,所以同时考虑精确度和时效,本文采用神经网络梯度下降优化训练200步。同时,图4和图5表明,惰行工况的建模效果均优于牵引工况和制动工况的建模效果,这是由于在该线路中,惰行工况只出现在恒速阶段(速度300 km/h左右)和停车制动阶段(速度160 km/h左右),情况较单一,数据特性较明显,模型的建立较简单;而牵引工况和制动工况是贯穿了从0到300 km/h的速度区段,运行模式较多,模型的建立较复杂。 建模是控制的前提,控制是建模的体现,因此本文基于多工况ANFIS模型采用广义预测控制方法对高速动车组进行运行控制,并与文献[13]基于全局ANFIS模型的广义预测控制和文献[7]基于线性多模型的广义预测控制进行对比验证。对高速动车组在京沪高铁线路的徐州东站—济南西站区间进行运行控制,验证三种建模方法的实用性和精确性。三种方法的速度跟踪曲线如图6所示,图7为速度跟踪误差曲线,图8、图9为加速度跟踪曲线和加速度跟踪误差曲线,图10为牵引力/制动力曲线。 图6 速度跟踪曲线 图7 速度跟踪误差曲线 图8 加速度跟踪曲线 图9 加速度跟踪误差曲线 图10 牵引力/制动力曲线 图6、图7表明基于多工况ANFIS模型的广义预测控制方法的速度曲线对给定速度曲线在牵引、制动、惰行工况下均有较好的跟踪能力,局部放大图显示两条线几乎重合在一起,且都在限速曲线范围之内,满足限速条件,动车组的安全性得到保证。跟踪的目标曲线是结合优秀驾驶员的动车组操纵经验,基于安全、正点和节能等运行指标,从大量高速动车组实际运行速度曲线中筛选确定的,其满足该趟车次的正点要求,速度的高精度跟踪确保了动车组的正点性。基于全局ANFIS模型的控制效果较好,满足正点性和安全性的要求,但从局部放大图中可以看到,跟踪精度较基于多工况ANFIS模型的要差一些。而基于线性多模型的控制速度曲线跟踪上存在一些速度偏差,跟踪效果相对较差,正点性受到一定影响。 图8~图10显示基于多工况ANFIS模型的加速度跟踪表现良好,且在±0.6 m/s2范围之内变化,满足人体舒适性条件(加速度小于1 m/s2,非常舒适)。同时,局部放大图中显示在不同工况转换时,控制力也变化平稳,降低了动车组运行的能源消耗。而基于全局ANFIS模型的加速度跟踪精度还需改善。基于线性多模型的加速度曲线、控制力曲线均具有不同程度的跳跃现象,影响乘客乘坐舒适性,加大动车组的运行能耗,表明线性多模型在不同线性子模型之间转换的平稳性还需提高。 本文提出高速动车组运行过程多工况ANFIS建模方法,通过分析高速动车组运行过程多种工况的受力情况,采用数据驱动多工况ANFIS实现动车组运行模型的有效建立,并基于多工况ANFIS模型设计相应广义预测控制器。对比试验表明:基于多工况ANFIS模型的动车组运行速度控制较基于全局ANFIS模型方法提高了速度和加速度的跟踪精度;较基于线性多模型方法具有更好的控制平稳性和跟踪效果,提高了动车组运行的安全性和正点性,为高速动车组自动驾驶提供了有力的技术支持。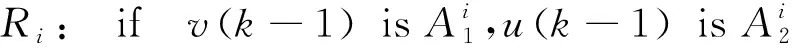
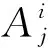
2.2 牵引ANFIS模型
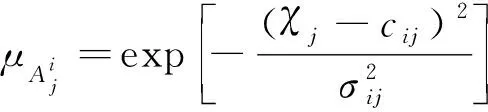
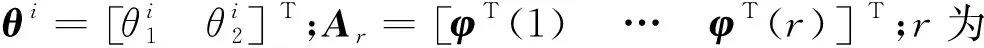
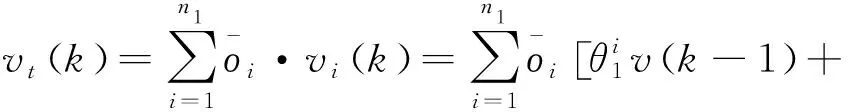
2.3 牵引ANFIS模型参数优化
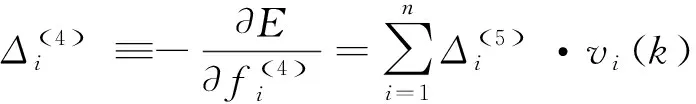
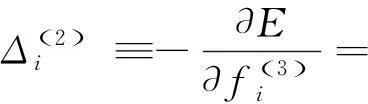
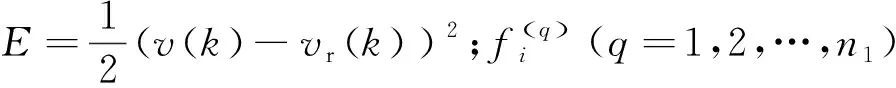
3 高速动车组运行控制
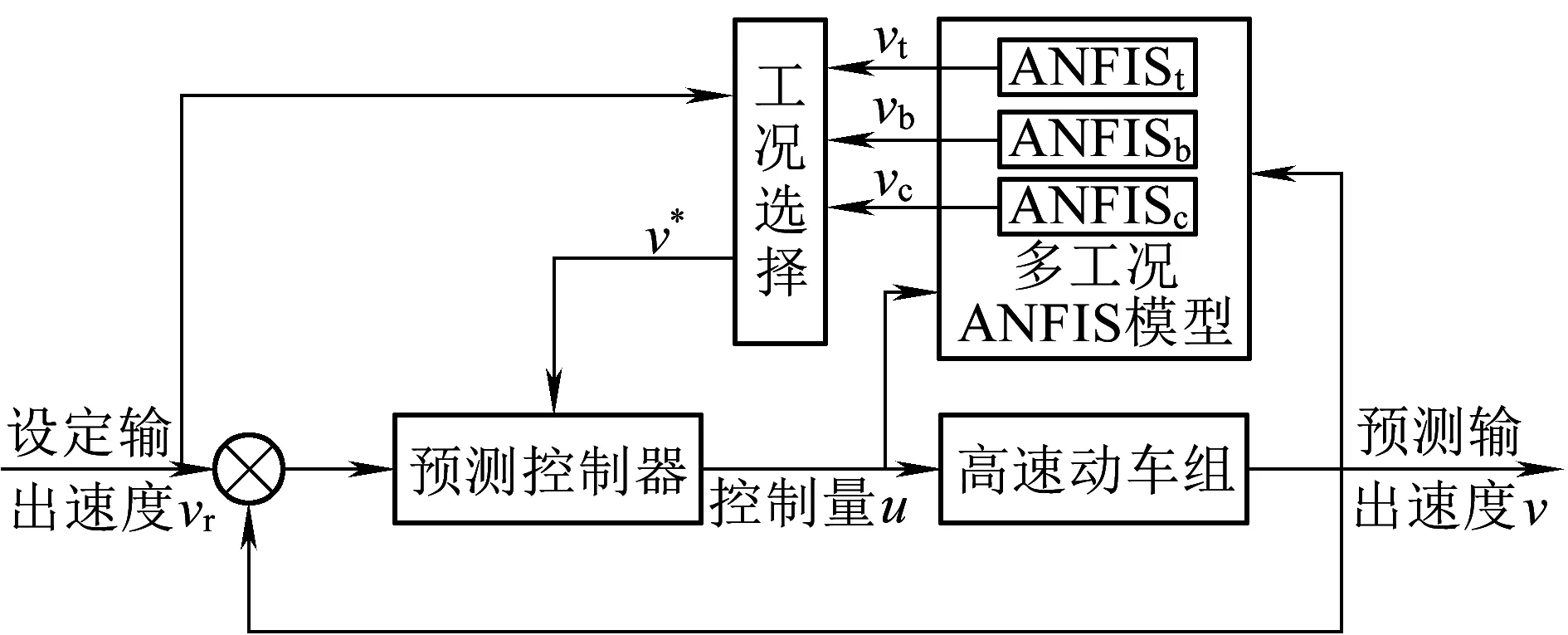
3.1 工况选择
3.2 预测控制器设计
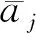
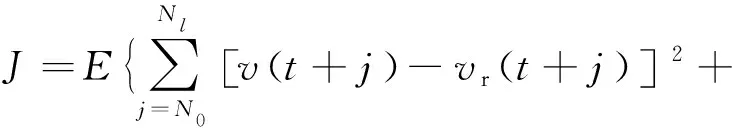
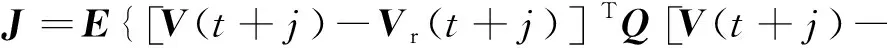
HΔU(t-j)+GV(t)
HΔU(t-j)-GV(t)]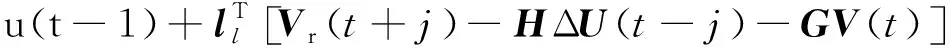
4 实验验证
4.1 建模验证
4.2 控制对比验证
5 结束语
