基于改进遗传算法的海上风电场消纳拓扑结构优化模型

赵东来，牛东晓，杨尚东，梁才

(1.华北电力大学 经济管理学院，北京，102206；2.国网(苏州)城市能源研究院 城市能源战略与规划研究所，江苏 苏州，215000；3.国网能源研究院 企业战略研究所，北京，102209)

近年来，海上风电以其能量密度高、风速稳定性强、对环境友好的特点，成为各国研究和开发的热点[1]。根据《可再生能源发展“十三五”规划》[2]，到2020年，海上风电开工建设1 000万kW，确保并网500万kW，海上风电已成为我国可再生能源发展的重要组成部分。海上风电场功率汇集系统是对海上风电进行汇集和传输的关键环节，包含大量的电气设备，在海上风电开发成本中占有很大比例，其总的建造成本占整个海上风电场的建造成本的15%～30%[3]。由于海上风电功率汇集系统电气元件繁多、电气连接方式多种多样，在设备选型、拓扑连接等方面有较大优化空间，国内外学者对此进行了大量研究。由于海上风电场功率汇集系统优化是基于多维度非线性、复杂度较高的多目标优化问题，需要应用遗传、进化等启发式优化算法[4-8]。ZHAO等[9]基于标准遗传算法从风机类型、电压等级、电缆选型、构成串等方面入手，对海上风电电气系统进行了优化设计，并得到几套风电场电气系统整体优化方案，着重对遗传算法的特性进行了分析；HUANG等[10]基于不同的进化算法，以建设成本最低为目标，对风电场内部电气系统进行了优化。但是，上述随机优化算法的计算量都很大且优化时间长。基于图论的各种算法也被应用于海上风电功率汇集系统的网络拓扑寻优[11-12]。DUTTA 等[13]基于最小生成树形成拓扑，并提出采用中间拼接点(Steiner point)的方式降低电缆使用长度，以降低网络一次成本；陈宁[14]基于模糊均值及图论对集电系统的网络拓扑进行了设计；DUTTA等[11]还利用最小生成树形成网络拓扑并通过蒙特卡洛方法评估了设计方案的可靠性。分步式的优化算法可以明显降低问题的维度，但上述方法默认的优化目标是电缆使用长度最小而不是电缆的投资成本最低，DUTTA等[13]提出的方法反而由于中间拼接点的引入而增加了投资成本。为此，本文作者提出一种改进的单亲遗传算法的多目标算法，以最大限度降低投资成本作为优化目标，基于模糊C均值算法(fuzzy C-means,FCM)对内部集电系统的拓扑节点进行分区，借鉴旅行商问题(traveling salesman problem,TSP)的优化求解思路，完成海上风电场功率汇集系统的拓扑结构求解。

1 海上风电场功率汇集系统

海上风电场功率汇集系统通常由海上风电机组、海底集电电缆、开关设备、变压器等设备组成，汇集系统将散布在风电场各处的风电机组发出的电能以一定的主接线形式进行汇集，通过海上升压站、海底高压输电电缆、陆上变电站接入陆上电网。目前已投运的海上风电场多为近海风电场，距陆地小于20 km，装机容量多在100 MW以下。海上风电场功率汇集系统的示意图如图1所示。

图1 大规模海上风电场功率汇集系统电气结构Fig.1 Electrical structure of large-scale offshore wind farm power collection system

集电系统通常采用交流拓扑结构，主要有链型、星型、单边环型、双边环型和复合环型等[14-15]，在工程上通常先将多台风电机组连接成串，再对各串进行连接，链型和复合环型是比较常见的拓扑结构[16]。对于小型风电场，一般通过功率汇集系统直接接入陆上变电站；对于具有上百台风机的大型风电场，一般需要建设海上变电站，通过输电系统接到陆上变电站并网。

2 海上风电场机群区域划分

对于存在多个海上变电站的大型海上风电场，由于风电机组对于每个海上变电站来说，地理位置各不相同，从而会造成连接成本上存在差异。因此，需要对海上变电站的数量、选址进行优化选择，并对风机集群的区域进行划分和分组。一般来说，地理位置相对接近的风电机组同属1个变电区域的可能性更大，本文采用FCM算法进行变电区域划分。

设海上风电场的风电机组台数为NWT，海上变电站的数量为Nsub，根据整个风电场和单个变电站容量给定海上变电站数目的范围为n∈[1，Nsub]，FCM算法的目的是将NWT个向量数据集划分为n个子集。取FCM的价值函数为

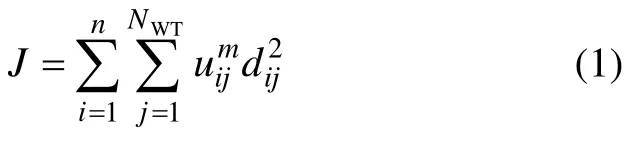
式中：m为加权系数，m∈[1，∞)；dij为第i个聚类中心(即海上变电站)与第j个数据点(即第j台风机)间的欧几里得距离，取；Xj为第j台风机节点位置为隶属度权重，介于0～1之间；Oi为群心(即第i个海上变电站的位置)。Oi的更新计算公式为

在第k次迭代中，若，则

3 海上风电场功率汇集系统优化模型

3.1 数学模型

海上风电场功率汇集系统投资成本的关键因素主要包括海上风电机组的数目和位置、海上升压变电站的数量和位置、网络拓扑连接方式、汇集导线的型号和长度。这里提出的优化模型主要是对海上风电场功率汇集系统的拓扑结构进行优化，以获得投资成本和可靠性的最优，因此，优化函数目标F可表示为

式中：Ct为投资成本；R为可靠性指标；λ1和λ2分别为经济性和可靠性评估的权重系数。总投资Ct可以表示为

式中：C0为海上风电场基本投资，主要包括各个风电机组的组成部分、安装费、土建费等固定成本；CC为海底电缆的投资成本；CS为海上升压变电站的投资成本。

由于汇集导线能够连接的风电机组数目取决于该导线的最大传输容量，为节约导线成本，不同汇聚处的风电机组馈线可选择不同截面的导线，如图2所示。

设C(Fj,i)为第j座升压变电站第i条馈线的投资成本，则汇集导线的成本可表示为

图2 第j座海上升压变电站第i条馈线Fig.2 Article ith feeder at the jth offshore booster station

式中：CCB为第i条馈线第m段线路造价；dm为该段线路的长度；为第i条馈线的段数。因此，优化问题可描述为

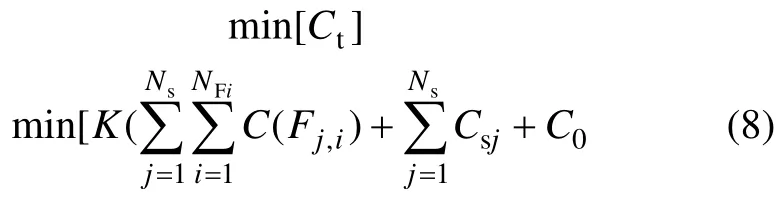
约束条件为

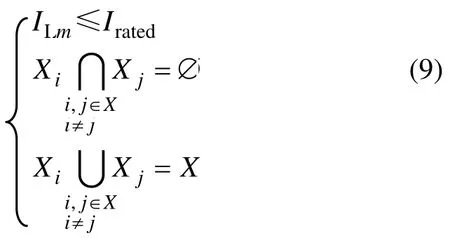
式中：Ns为海上升压变电站的数目；NFi为第j座升压变电站馈线数目(即与升压平台相连接的串数)；Csj为第j座升压变电站的投资成本；ILm为F(j,i)条馈线中第m段线路运行电流；Irated为该线路的额定电流；X为升压变电站和风电机组节点的集合。

3.2 改进单亲遗传算法

由上述模型可知，海上风电场汇集系统成本影响因素较多，且彼此之间关系密切，这些因素为离散变量，且呈非线性，由此在成本最优目标下的拓扑连接优化问题非常复杂。遗传算法(genetic algorithm,GA)在全局搜索和函数优化中具有明显优势，因此，大多用于解决离散性多变量多目标非线性优化问题[17]。传统的GA算法都基于双亲繁殖方式，在采用序号编码方式解决组合优化问题时，采用常规的交叉算子计算方法会出现基因缺失或基因重复现象，具有一定局限性。而单亲GA算法由于所有操作均在单个个体上进行，因此，遗传操作过程更简单，寻优效率更高。本文提出一种改进的协同进化单亲 GA算法，并借鉴 TSP[18-19]优化求解，比单亲GA算法具有更高寻优效率。

3.2.1 确定编码方式与适应度函数

在用GA算法对汇集系统进行拓扑优化设计时，需要首先对风电机组进行顺序编号，染色体每一位基因与风电机组序号一一对应，且能够反映各风电机组之间的网络联系状况，在整个求解过程中无需进行编码解码操作。以汇集系统投资成本Ctotal作为适应度函数f，则有

3.2.2 种群分组遗传操作

首先将风电场的所有机群进行分组，对于每组机群都采用最优保存策略，这样能保证全局收敛效果[13]。对于每组机群的父代最优个体，基于一定概率进行基因重组操作，如基因的换位、移位和倒位，在产生新的个体后进行种群更新，一直到最优个体收敛或到达迭代次数时，算法终止。

3.2.3 改进单亲遗传进化算法步骤

改进单亲遗传算法流程如图3所示。

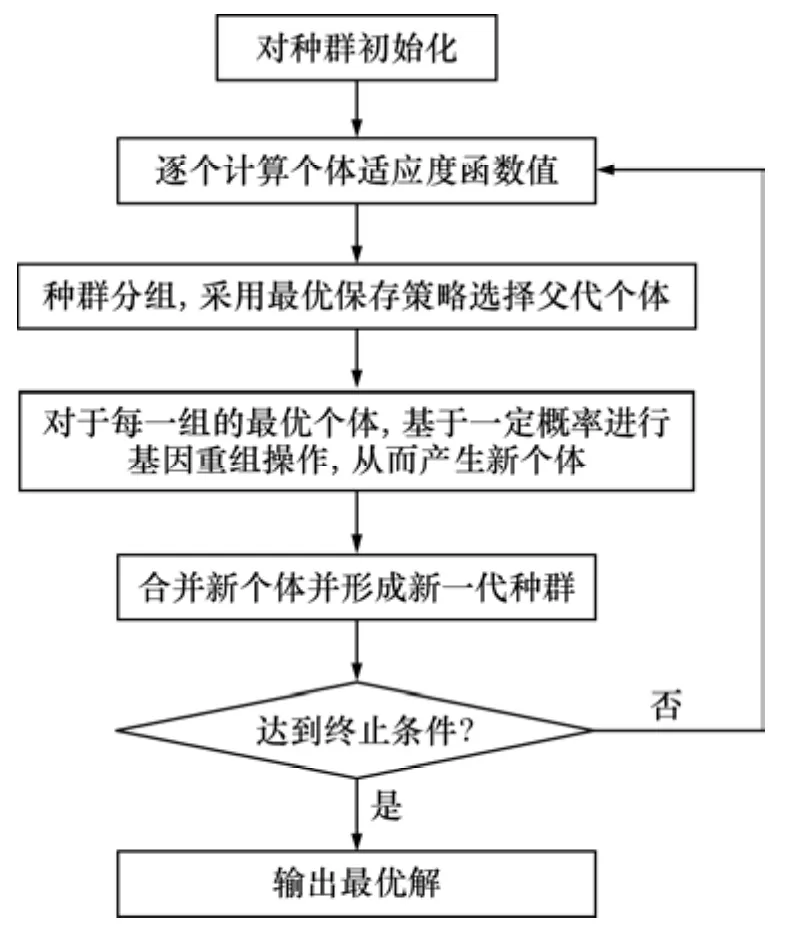
图3 改进遗传算法流程Fig.3 Flow path of modified genetic algorithm

3.3 功率汇集系统的可靠性评估

可靠性是表征电力系统能够向用电客户提供不间断的、高质量电能需求的能力。功率汇集系统的可靠性评估主要是为了确保功率汇集系统拓扑结构在经济性最好的同时还能保证较高的可靠性；另一方面，功率汇集系统不间断的供电能力在一定程度上可以保证海上风电场的经济效率，这对投资成本的回收也是重要影响因素。

为了评估汇集系统拓扑结构的可靠性，对汇集系统的结构进行适当简化，主要考虑风电机组、集线电缆、开断设备故障的情况。风电机组的故障发生概率为λG，汇集电缆是1个串联系统，它由1段电缆及2侧开关构成，主要包括近侧负荷开关、汇集电缆、远侧负荷开关，图4(a)和(b)所示分别为海上风机之间相联和风机与变电站相联的简化示意图。

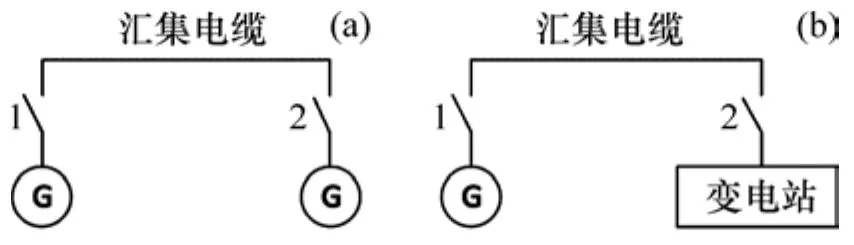
图4 汇集电缆系统Fig.4 Gathering cable system

汇集电缆元件的等效停运概率λcable为

其中：λi为第i个元件故障率。可靠性指标选用风电功率汇集系统的等效容量SEQ，评估风功率汇集点的平均出力。

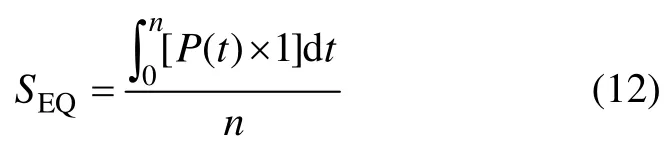
式中：n为仿真时间，取整；P(t)为第t次仿真的平均可用容量。可靠性指标的计算步骤为：首先，设定风机单元和集线电缆的故障率，基于蒙特卡洛算法随机产生故障序列；其次，判断元件开断状态和拓扑结构的连通性；最后，计算系统可靠性。

汇集系统拓扑优化设计流程如图5所示。

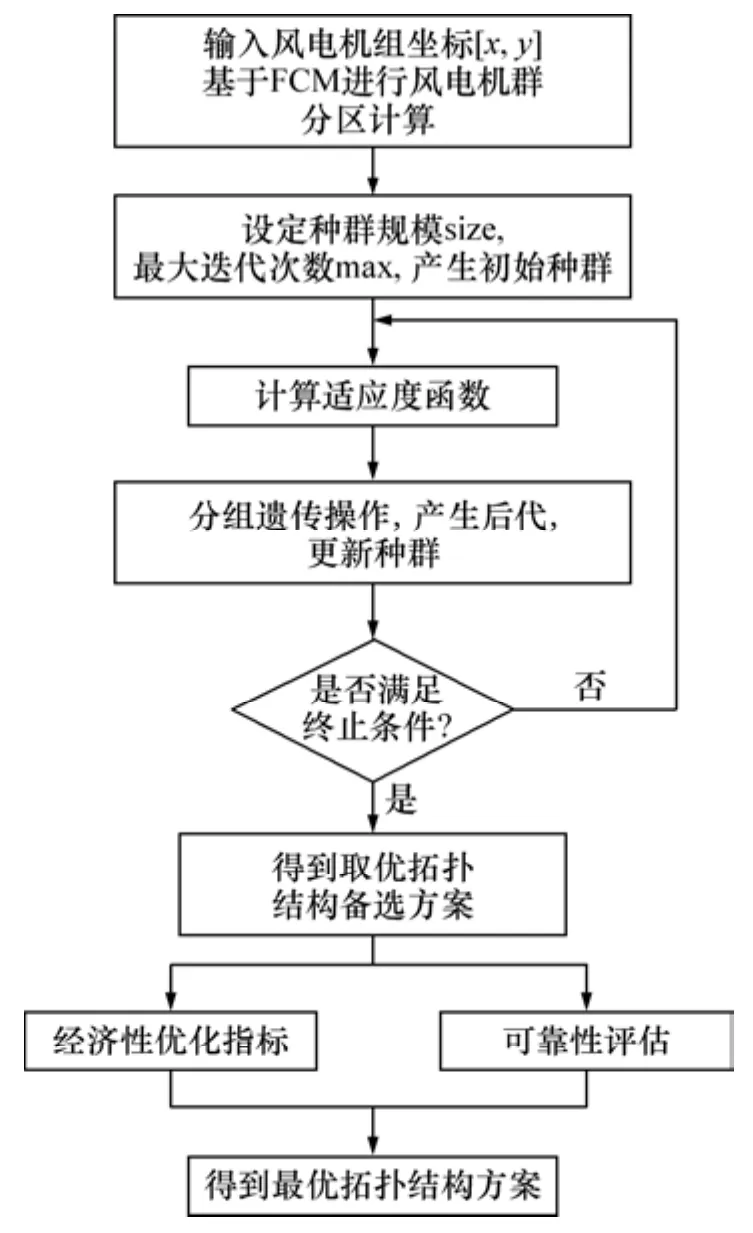
图5 海上风电场功率汇集系统拓扑优化流程Fig.5 Topological optimization design process of power collection system of offshore wind farm

4 算例分析

以某大型海上风电场为例，预计装机容量为100 MW，每台风电机组容量为1 MW，计划每10台机组汇集到母线后升压至35 kV，再通过2台50 MVA变压器升压到110 kV电网。基于FCM算法的风电机群区域划分方法，将整个风电场群分为10个区域，每个区域内10个风电机组。最终的区域划分结果如图6所示。

图6 海上风电场区域划分结果Fig.6 Divided areas of offshore wind farm

为方便说明，将区域②内的发电机组集电系统按本文方法进行优化计算，得到在不同串数下区域内拓扑连接方案如图7所示，其中的交汇点为根据 FCM算法确定的集群风电机组的群心，即为35 kV海上升压变电站的位置。

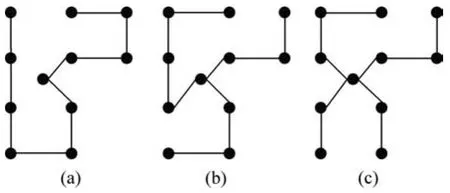
图7 区域②的拓扑优化结果Fig.7 Topological optimization results of area ②

根据式(4)，将经济性和可靠性评估的权重系数λ1和λ2分别设置为0.75和0.25，则不同串数下的拓扑连接方案下的经济性指标、可靠性指标以及优化目标指标如表1所示。

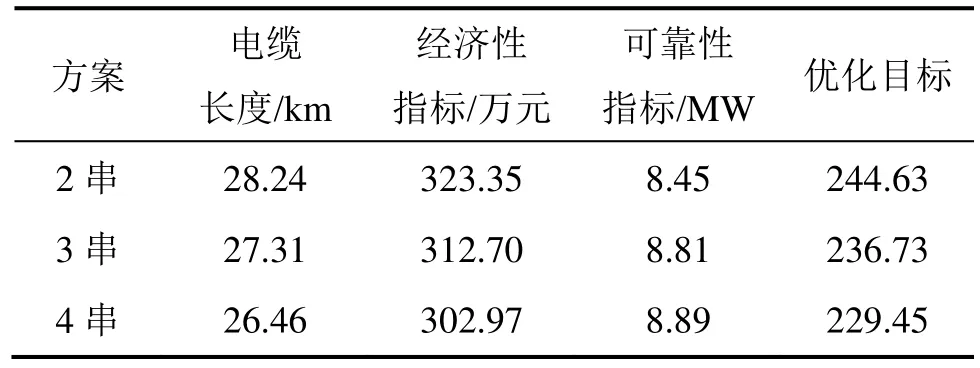
表1 不同拓扑优化方案的经济性及可靠性对比Table 1 Comparison of economy and reliability of different topological optimization schemes

经济性指标与基本投资、海上升压投资和电缆长度有关，计算结果表明经济性指标与电缆长度基本呈正向关系，在保证电缆长度最小的基础上实现可靠性最优是拓扑优化的目标，3种优化方案中四串方案电缆长度最短，经济性指标最低且可靠性最优，所以，选择4串方案作为优选方案。

对于海上风电场各个区域的集电系统，选择不同的权重系数λ1和λ2进行经济性和可靠性最优计算，可以得到整个海上风电场的分区域拓扑连接状况如图8所示。各区内的35 kV汇集点再次形成10个节点组成的集群，通过本文提出的方法进行2次优化，即可得到汇集点的拓扑连接方案，最终汇集到110 kV终端变电站并入电网。

图8 功率汇集系统拓扑优化结果Fig.8 Topological optimization results of power pooling system of offshore wind farms

基于改进前后的单亲遗传算法计算目标函数曲线收敛效果如图9所示。

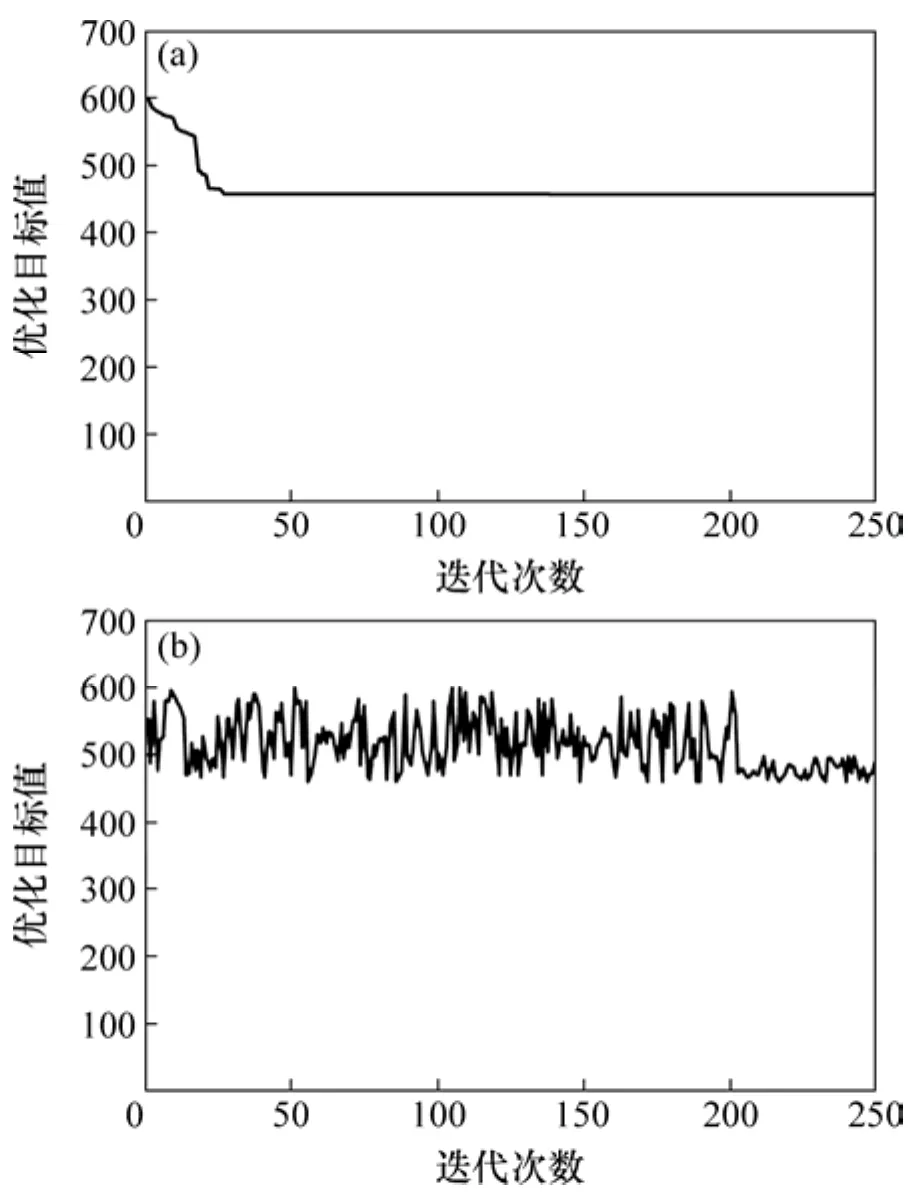
图9 本文提出算法和常规单亲GA算法的收敛效果对比Fig.9 Comparison of convergence effect between algorithm in the paper and conventional single GA algorithm

综合上述优化结果可以看出：

1)基于FCM方法可以便捷的根据需求将海上风电场风机进行分组分群，通过计算群心位置求得海上升压变电站的地理方位。

2)基于海上功率汇集系统优化模型，在设定接线方案评估权重的基础上，可以方便地求得经济性和可靠性综合最优的接线方案。

3)本文提出的算法与常规单亲遗传算法相比，只需26次计算就可以求得最优解，寻优效率更高，收敛效果更好。

5 结论

1)根据风电机组与聚类群心的欧几里得距离，提出基于 FCM 算法的海上风电场机群区域划分方法，从而可将地理位置较接近的机组进行科学划分。

2)综合考虑海上风电场各部分的投资成本和汇集系统元件设备的可靠性，构建了海上风电场功率汇集系统优化模型，可对经济性和可靠性权重进行设置，从而得到不同侧重下的拓扑结构优化目标。

3)改进的单亲遗传算法用于海上风电场汇集系统优化模型的迭代求解，与传统遗传算法相比，可以取得更高的寻优效率和更好的收敛效果，从而为大型海上风电场建设中的功率汇集系统拓扑优化设计提供参考。