近爆冲击波和破片复合作用下预应力钢筋混凝土空心板梁的损伤效应分析

田力，李永欣



近爆冲击波和破片复合作用下预应力钢筋混凝土空心板梁的损伤效应分析

田力1, 2，李永欣1

(1.天津大学 建筑工程学院，天津，300072；2. 天津大学 滨海土木工程结构与安全教育部重点实验室，天津，300072)

通过数值分析研究预应力钢筋混凝土空心板梁在近爆冲击波和预制破片复合作用下的损伤情况。通过非线性有限元软件ANSYS/LS_DYNA模拟预应力混凝土板的爆炸试验和炸药驱动预制破片的试验，验证本文所采用的材料本构模型及技术路线的合理性与可靠性，研究爆炸波、破片荷载及二者复合作用下预应力空心板梁的动态响应的差异，同时运用参数化分析方法，研究张拉控制应力、预应力损失水平、混凝土强度、普通钢筋纵筋配筋率及箍筋间距对空心板梁动力响应的影响。研究结果表明：随着张拉控制应力增大，构件的抗爆性能显著增强；在相同张拉控制应力作用下，即使构件有不同水平的应力损失，其抗爆性能也基本相同；提高混凝土强度对构件的抗爆性能的提升作用并不明显；普通钢筋纵筋配筋率的提升在一定范围内可以小幅度提高构件的抗爆性能；随着箍筋间距增加，构件的抗爆性能明显减弱。

预应力钢筋混凝土空心板梁；爆炸波；破片；复合作用；参数化分析

近年来，我国经济飞速发展，大跨度建筑物数量日益增多，尤其是大跨度桥梁，这也促进了预应力混凝土的发展。预应力混凝土结构具有截面面积小、抗裂性能好、经久耐用等一系列优点。但是，由于恐怖袭击事件以及日常生产中的意外事件频发，设计人员不得不考虑结构的抗爆设计。预应力混凝土结构一般具有较大的跨度，而预应力混凝土梁是其主要的承重构件，一旦发生爆炸破坏，必然会造成严重的经济损失及大量的人员伤亡，因此，研究预应力钢筋混凝土梁构件在爆炸冲击荷载作用下的动力响应与损伤破坏具有很重要的现实意义，可为结构的抗爆设计及防护提供参考。目前，人们对钢筋混凝土结构的抗爆性能进行了大量研究，但关于预应力钢筋混凝土结构抗爆研究很少。李砚召等[1]开展了后张无黏结部分预应力混凝土梁板柱形结构模型在平面装药爆炸条件下的大比尺化爆相似模拟试验；CHOI等[2]研究了无黏结预应力混凝土板在25 kg铵油炸药作用下的抗爆性能，构件长×宽×高为1 400 mm×1 000 mm×300 mm；CHEN等[3]利用有限元软件LS-DYNA模拟了截面长×宽为220 mm×160 mm、跨度为2 600 mm的预应力混凝土简支梁在爆炸波作用下的响应；刘超[4]采用非线性显式有限元软件AUTODYN建立了简化截面形式的预应力混凝土梁爆炸模型，通过改变相关参量进行了数值分析；夏小虎[5]采用LS-DYNA软件模拟了预应力混凝土梁在爆轰条件下的动力响应。国内外关于预应力混凝土结构的抗爆性能的试验及模拟研究较少，有关预应力混凝土结构在冲击波和预制破片复合作用下的研究更是未见报道，预应力钢筋混凝土结构的抗爆性能尚不明确。预应力钢筋混凝土梁构件对于整体预应力结构有重要作用，因此，有必要详细地研究预应力钢筋混凝土构件在爆炸荷载作用下的动力响应与损伤情况，研究不同参数下构件的抗爆性能，以便找出提高结构抗爆性能的最优方法。关于破片和爆炸波的复合作用，田力等[6−7]指出爆炸波和破片复合作用时对结构的破坏作用大于二者单独作用的线性叠加。本文基于非线性有限元软件LS-DYNA，模拟在公路桥梁中广泛应用的预应力钢筋混凝土空心板梁在近爆冲击波和预制破片复合作用下的动态响应，运用参数化分析方法研究张拉控制应力、混凝土强度、配筋率等因素对构件在近距爆炸波和预制破片复合作用下动力响应的影响规律。

1 有限元模型及数值分析方法

1.1 模型简介

本文选取实际桥梁工程中较为常见的预应力空心板梁为研究对象，研究其在冲击波和预制破片复合作用下的动态响应及损伤破坏。空心板梁有限元模型如图1所示。该空心板梁为先张法预制空心板梁，其标准跨径为10 m，截面尺寸及配筋图如图2所示。钢筋直径低于1 cm的采用HPB235钢筋，其余均采用HRB335钢筋；预应力钢绞线采用抗拉强度标准值ptk为1 860 MPa，公称直径为15.2 mm的低松弛高强度钢绞线。梁两端采用简支约束，通过在梁两端建立相应的刚性支撑，定义二者面面接触的方式，来实现简支约束。

DAVID等[8]关于车辆爆炸对桥梁损伤破坏的研究结果表明：车辆爆炸时桥梁的破坏形态与一定量的炸药造成的破坏效果相同(炸药质量为100~450 kg，且炸药的位置距离梁体上表面的距离约为1.2 m)。本文作者在选择炸药质量时考虑到梁体上部桥面层的影响以及前期在构件层次上的研究，适当地缩减了炸药质量，取炸药质量为60 kg，保证炸药距离梁体上表面的距离为1.2 m。炸药采用立方体型，其边长为40 cm。考虑到炸药爆炸时破片的飞散形式一般是以轴心对称形式向四周飞散，除底面外其他5个面的破片对结构的影响几乎可以忽略不计，故只在炸药底面均匀地布置预制破片，破片边长为1 cm(见图1(b))，炸药采用中心起爆。由于构件较长，且近距爆炸产生破坏效应具有局部性，考虑到计算成本及时间效率，参考文献[9]，将空气域长×宽×高选为300 mm×102 mm×244 cm。模型中钢筋选用beam161单元，混凝土、空气、炸药及破片均采用solid164单元，钢绞线选用link160单元，混凝土单元最大边长为1.5 cm，约170万个单元，钢筋及钢绞线单元边长为1.0 cm，共计1万个单元，炸药单元边长为2.0 cm，共计0.8万个单元，空气单元的最大边长为3.0 cm，约40万个单元，空气和炸药采用ALE(arbitary Lagrange-Euler)算法，整个计算模型共计约212万个单元。

图1 空心板梁有限元模型

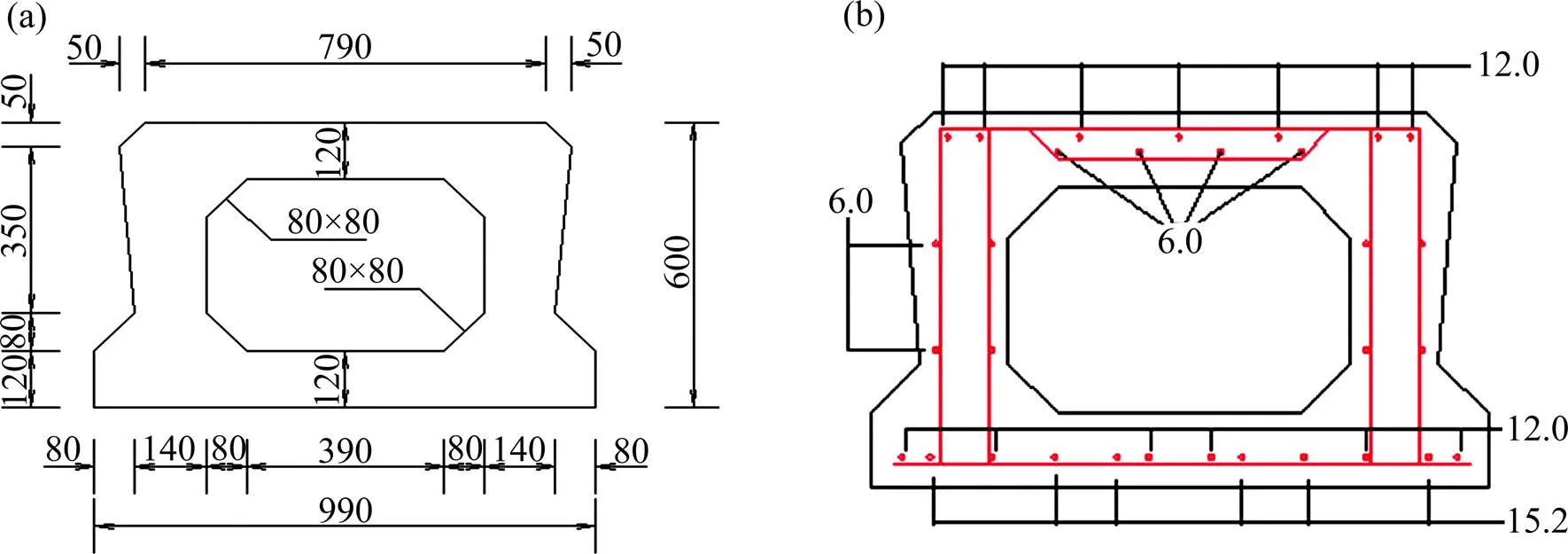
数据单位：mm

1.2 数值分析方法

建立模型时，钢筋和混凝土采用共节点法建模，不考虑它们之间的黏结滑移效应[10]，这种建模方式具有较高的准确性。为避免共节点法存在初始渗透，产生负的滑移界面能，在接触控制中设置关键字参数IGNORE=1，空心板梁、破片群与空气及炸药之间采用罚函数耦合算法，破片与空心板梁设置为面面侵蚀接触，破片群自身设置为自动单面接触，时间步长比例因子取0.67。为了控制大变形带来的问题，采用单点积分沙漏模态，采用刚性沙漏控制，沙漏系数 取0.03。

在进行计算之前需给空心板梁施加相应的预应力，预应力的施加方法有等效荷载法和实体力筋法，实体力筋法又包括初应变法和降温法。本文模型采用分离式建模，预应力的施加方法采取较常用的降温法，通过降低预应力钢绞线单元的温度，使得钢绞线收缩从而产生预应力。该方法比较简单，且可以模拟应力损失[11]。

由于预应力的存在，在进行动力计算之前需要考虑前期静力即预应力影响，需要先执行1次稳态或准静态分析，目的是将稳态分析结果中的位移、温度作为体载荷施加到相关节点上，实现相应部件的应力初始化，作为后续动力分析的初始条件。爆炸荷载作用于结构的时间非常短，且在模型计算时，时间的控制一般都是以ms计，若直接给构件施加预应力而不考虑预应力的初始化，则当爆炸荷载作用时，预应力构件尚未处于稳定的应力状态，将使后续计算的结果存在较大的误差，不具有实际参考价值。

为使得结构在进行动力计算之前处于稳定状态，本文采用动力松弛的方法来实现应力的初始化。该方法通过能量收敛准则对平衡状态进行判断[12]，当达到收敛标准时，软件自动停止动力松弛进而继续后续的动力计算。在达到计算精度要求的情况下，通过关键字*CONTROL_DYNAMIC_RELAXATION适当地调整收敛准则，可以提高计算效率。

1.3 材料模型及参数

混凝土的强度等级为C50，混凝土采用双线性随动强化模型*MAT_CONCRETE_DAMAGE_REL3(73号材料)，相比于其他混凝土模型，该模型能够有效地模拟钢筋混凝土在高应变率下变形的力学性能[13]，该模型只需要提供混凝土的轴心受压强度即可。钢筋采用双线随动强化模型*MAT_PLASTIC_KINEMAT- IC(3号材料)，二者都可以考虑到其应变率效应；钢绞线采用*MAT_ELASTIC_PLASTIC_THERMAL (4号材料)来模拟，以便通过降温法来施加相应的预应力，钢绞线的极限抗拉强度标准值ptk为1 860 MPa，张拉控制应力为0.75ptk。

空气采用*MAT_NULL模型及*EOS_LINEAR_ POLYNOMINAL状态方程描述，其表达式为

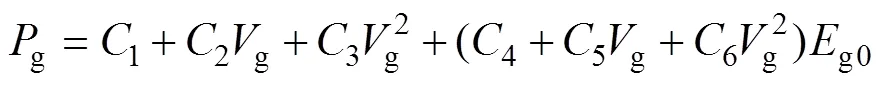
式中：g为空气压力；0，1，2，3，4，5和6均为常数(其中1，2，3和6取值为0)；g0为单位体积空气的初始内能；g为相对体积。空气参数见表1。

表1 空气参数

铵油(ANFO)炸药采用*MAT_HIGH_EXPLOSIV- E_BURN模型及JWL状态方程描述，其表达式为

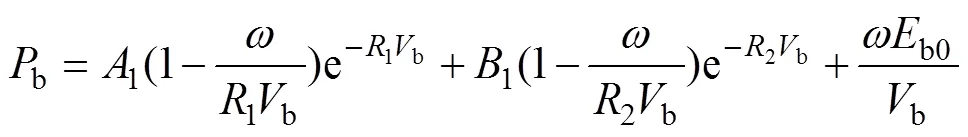
式中：b为爆轰压力；b为相对体积；b0为单位体积炸药初始内能；1和1为材料常数；1，2和为试验拟合参数。炸药参数见表2。预制破片采用钨合金材料，忽略破片在加速及侵彻混凝土过程中的变形及损伤，将破片视为刚体[14]，采用*MAT_RIGID材料模型描述，破片密度为17 800 kg/m3，弹性模量为357 GPa，泊松比为0.2。

2 数值模型的有效性验证

2.1 近爆冲击波作用下预应力混凝土板试验验证

本文通过文献[2]中的已有试验验证文中所采用的耦合算法、接触类型和本构模型的合理性。文献[2]中试验构件长×宽×高为1 400 mm×1 000 mm×300 mm，是1块后张法无黏结预应力混凝土板，混凝土强度等级为C40，炸药采用25 kg的铵油炸药，炸药安放在构件中心点处，距离构件1 m。为了研究预应力对构件抗爆性能的影响，进行1组对比试验，第1个构件钢绞线中施加的预应力为580 kN，第2个构件钢绞线中施加的预应力为820 kN。钢绞线的位置及模型尺寸如图3所示。

试验中测得2个构件的背爆面中点的位移，进行数值模拟时按照原试验条件建立有限元模型，混凝土、空气及炸药采用solid164单元，钢绞线采用link160单元。为了得到较准确的计算结果，单元网格边长较小，模型中所采用的耦合算法、接触类型和材料本构模型均与本文1.3节中的相同。构件背爆面中点位移试验结果与数值模拟结果对比如图4所示(其中负号表示位移方向向下)。

从图4(a)可以看出：当钢绞线中施加预应力为580 kN时，试验构件背爆面中点的最大位移为 −7.14 mm，数值模型中构件底部中点的最大位移为−7.20 mm；当预应力为820 kN时，试验中构件背爆面中点最大位移为−6.48 mm，数值模拟中构件背爆面中点的最大位移为−6.34 mm。由此可见，数值模拟精确程度相当高，误差均在2%以内。从图4还可以看出：模拟峰值位移有提前的现象，这与建模时钢筋与混凝土采用共节点建模而忽略了它们之间的黏结滑移效应有一定的关系，但是模拟的位移曲线与试验测得的曲线走势基本相同，且最大值精度较高，说明本文采用的材料本构模型能够较好地模拟近爆冲击波作用下预应力混凝土构件的动力响应。

表2 炸药参数

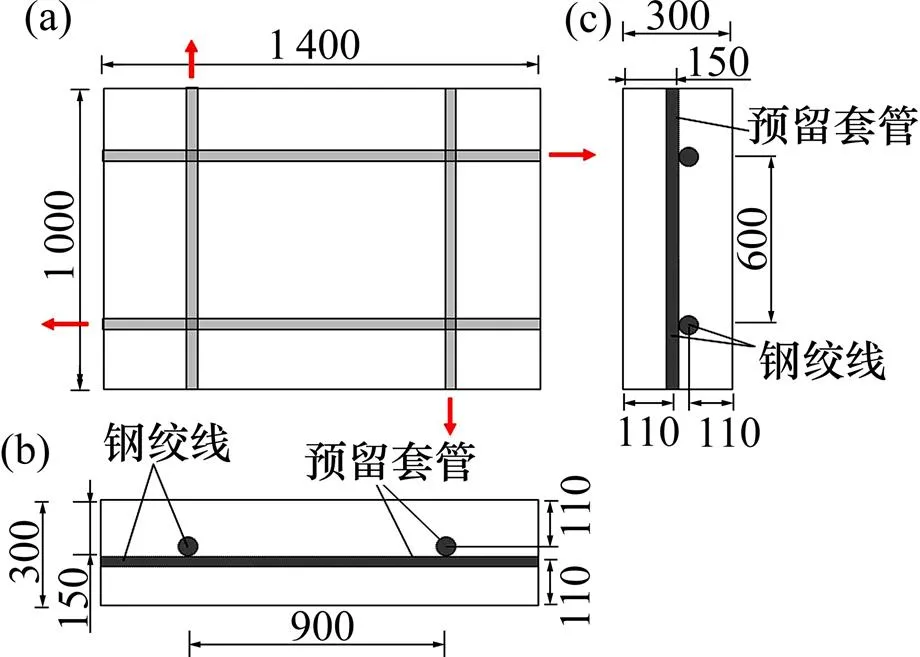
数据单位：mm

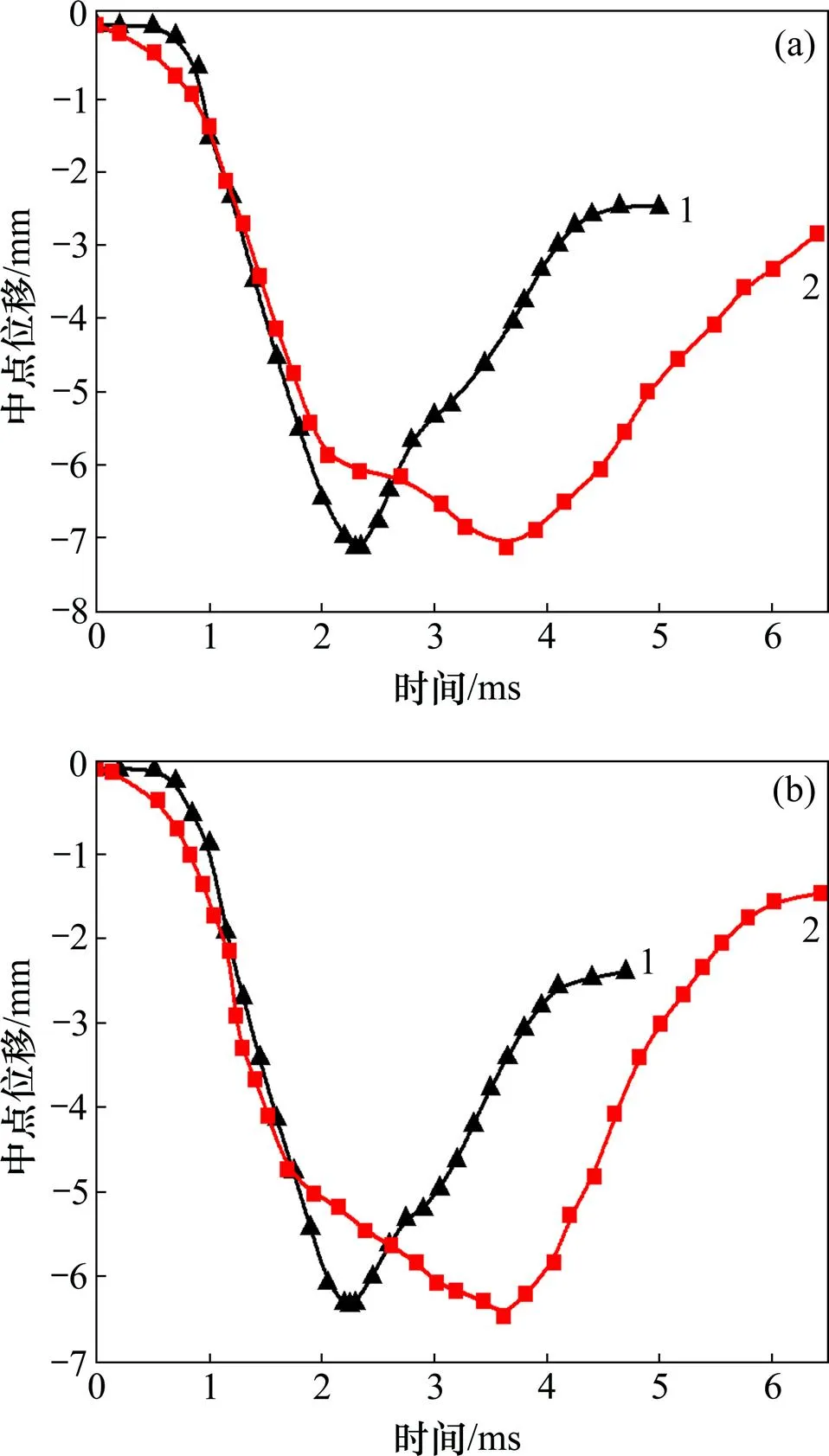
预应力/kN：(a) 580；(b) 820

2.2 炸药驱动破片速度验证

炸药爆炸后预制破片在爆炸波的驱动下向前飞散，其速度是它们发挥侵彻作用的关键因素。本文作者参考文献[15]中的试验，对破片速度进行验证。试验采用圆柱形炸药，炸药直径为12.6 cm，炸药柱的长径比为2，药柱外侧黏附边长为0.9 cm的钢立方体预制破片，周边紧密排列共计50个，试验时采用测速设备测得破片飞散后的速度为2 082 m/s。本文按照其实际的情况运用LS-DYNA建立预制破片、炸药及空气流固耦合模型。将本文数值模拟得到的预制破片炸药爆炸后的速度−时间曲线与文献[15]中通过AUTODYNA软件模拟得到的破片速度−时间曲线进行对比，如图5所示。由图5可知：LS-DYNA模拟的预制破片飞散速度为2 100 m/s，与试验结果的相对误差为0.58%，误差较小，且与AUTODYN模拟的速度−时间曲线误差也较小。因此，可以认为数值模拟爆炸波驱动预制破片的方法是可靠的。

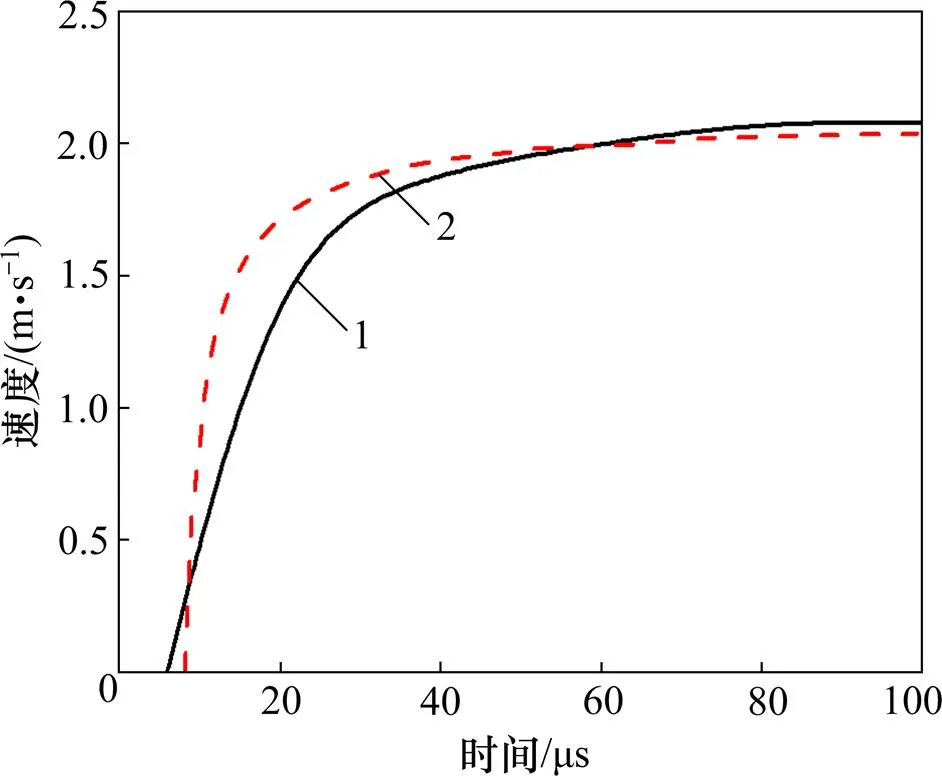
1—LS-DYNA模拟；2—AUTODYNA模拟。

3 爆炸波作用、破片群作用及二者复合作用下预应力空心板梁动态响应对比

图6(a)所示为爆炸波、破片群及二者复合作用下空心板梁底部混凝土中点的竖向位移时程曲线，其中点为正对炸药中心最底部混凝土上的中心点；图6(b)所示为空心板梁上部混凝土中纵向钢筋点的竖向位移时程曲线(和点位置示意图见图1(c))。从图6(a)可以看出：爆炸波单独作用、破片群单独作用及二者复合作用时空心板梁点最大竖向位移依次为−5.80，−5.04和−6.07 cm，其残余位移分别为−4.50，−5.04和−6.07 cm，虽然爆炸波单独作用时的最大竖向位移和二者复合作用下位移相比增幅不大，仅4.4%，但爆炸波作用时点的竖向位移有明显回弹，而破片单独作用和二者复合作用时点的残余位移和最大位移相同，没有发生回弹。这是因为当破片存在时，破片具有局部穿甲效应，使得空心板梁上部混凝土被击穿，构件发生局部破坏。空心梁局部破坏情况见图7。爆炸波单独作用时，构件损坏情况较轻，没有明显的局部破坏。图6(b)中钢筋中点的竖向位移也说明了这一点，破片单独作用和二者复合作用下点的竖向位移基本相同，位移约为−18.6 cm，而爆炸波单独作用时其位移为−6.97 cm，前者位移为后者的2.67倍，二者均发生了局部破坏。

以上结果说明在近距离爆炸作用下，当有破片存在时结构往往会发生较为明显的局部破坏，这对结构的抗爆性能是不利的，当承重构件发生局部破坏时，往往会造成整个构件继续破坏，使其丧失承载力。因此，在抗爆设计中应当考虑破片的局部穿甲效应。

图7 空心板梁局部破坏

4 冲击波与破片群复合作用下预应力空心板梁损伤的参数分析

4.1 张拉控制应力对空心板梁动力响应的影响

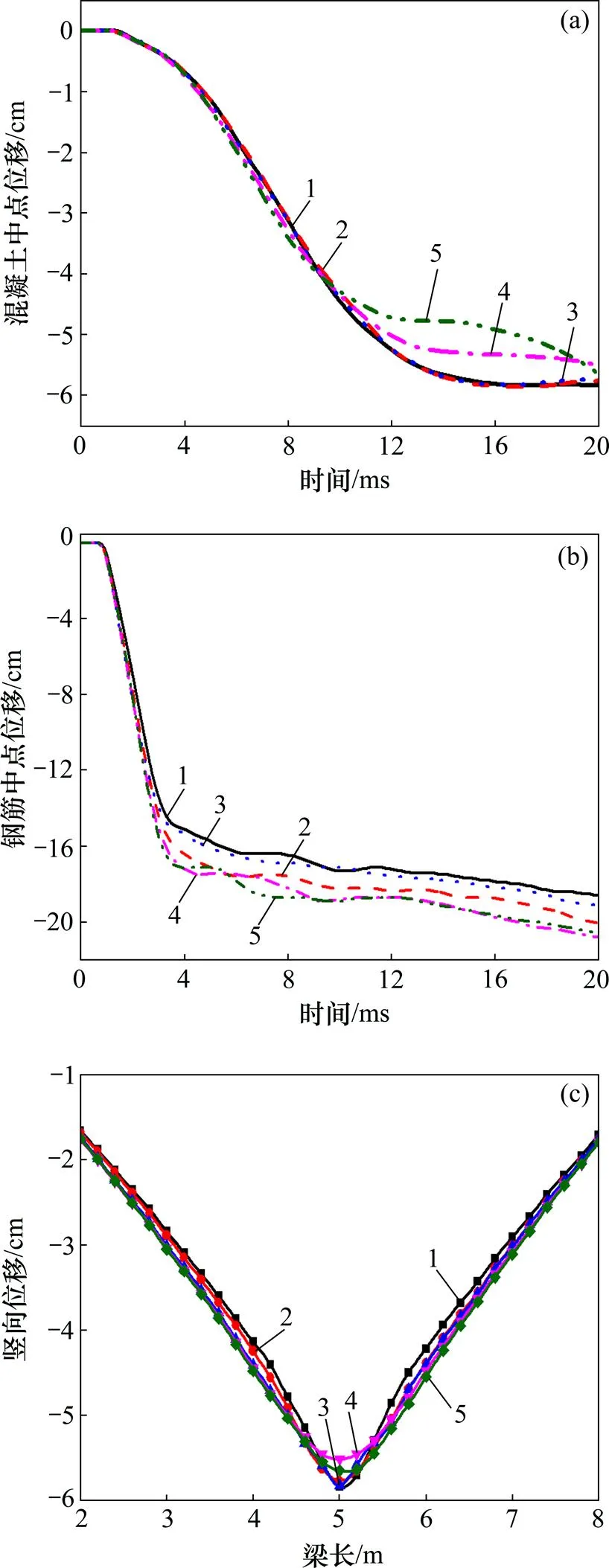
预应力水平对预应力构件的抗爆性能具有重要的影响，本文模拟张拉控制应力分别为0.75ptk，0.65ptk，0.55ptk和0.45ptk以及未施加预应力这5种工况，且通过降温法较好地模拟了预应力的损失情况，前4种工况的应力损失约为其张拉控制应力的10%。空心板梁底部混凝土中点(点)及上部钢筋中点(点)的竖向位移分别如图8(a)和图8(b)所示。该空心板梁的计算跨径为10 m，为了研究整个梁长方向的竖向变形情况，在梁长2~8 m的范围内每隔0.2 m选取1个点，所有点均为底部混凝土中心轴线上的点，空心板梁位移竖向位移峰值分布如图8(c)所示。

由图8(a)可知：随着预应力水平提升，空心板梁点的竖向位移逐渐减小。在20 ms，当张拉控制应力为0.75ptk时，点的最大竖向位移为−6.07 cm，未施加预应力时构件点的最大竖向位移为−9.35 cm，增大54.04%，且从曲线的走势可以看出其位移呈继续增大趋势，可知施加预应力的混凝土构件的抗爆性能明显强于同样条件下未施加预应力的构件的抗爆性能。总体来看，随着张拉控制应力增加，构件的抗爆性能增强，这是由于预应力存在时构件中混凝土和钢筋处于较高的应力水平，在一定程度上增加了构件的抗弯性能。从图8(b)可知：不同张拉控制应力作用下钢筋点的竖向位移大致相同，这是因为在破片和爆炸波复合作用下，构件均发生局部破坏，致使其上部钢筋的位移基本相同。从图8(c)可以看出：空心板梁竖向位移在梁长为4~6 m的范围内差距较大，这是因为炸药和破片处于梁长为5 m的正上方，故爆炸冲击作用在梁长4~6 m的范围内较明显。

(a) 底部混凝土中点位移时程曲线；(b) 上部钢筋中点位移时程曲线；(c) 空心板梁竖向位移峰值分布图

对梁体损失的混凝土质量进行统计，5种工况下混凝土损失的质量占梁体的总质量的比例分别为4.14%，4.25%，4.39%，4.62%及5.12%。从质量损失比上也能看出梁体的局部损伤情况逐渐加重。

4.2 应力损失对空心板梁动力响应的影响

在实际生产生活中，先张法预应力混凝土构件由于放张时混凝土弹性压缩、钢筋松弛、混凝土徐变等一系列原因，往往会导致构件中预应力降低，预应力损失的总和约占张拉控制应力的10%~30%[16]。张拉控制应力取为0.75ptk，是实际生产中最常用的张拉控制应力，通过降温法调节温度，使得其预应力损失总和分别占张拉控制应力的12%，16%，20%，24%和30%。

图9所示为不同应力损失下空心板梁位移曲线图。从图9可知：当应力损失总和占比不同时，不同工况下预应力空心板梁点的最大位移的增幅仅为5.6%，钢筋中点的位移增加幅度仅为4.8%。从图9(c)也可以看出：仅在梁长为4.5~5.5 m的范围内空心板梁峰值位移有较小差距，其余范围内基本完全相同，且在后期查看结果时发现它们的破坏情况也基本相同，这5种情况下混凝土损失的质量占梁体总质量的比例最小为4.14%，最大为4.25%，质量损失比也基本相同。由此可见：当张拉控制应力为0.75ptk时，即便是构件有不同水平的应力损失，但其抗爆性能基本相同。这是由于虽然构件有不同的应力损失，但构件内整体上应力变化并不是很大，所有构件均处于较高的应力水平。若对预应力空心板梁划分抗爆等级，张力控制应力为0.75ptk的构件即使有不同的应力损失，它们也完全可以划分为同一抗爆等级。

4.3 混凝土轴心抗压强度对空心板梁动力响应的影响

分别模拟混凝土轴心抗压强度为50，55，60， 65和80 MPa时，爆炸波与破片复合作用下预应力空心板梁的破坏情况，期间保持张拉控制应力为0.75ptk，其他参数不变。

图10所示为不同混凝土轴心抗压强度下空心板梁的位移曲线。由图10可知：随着混凝土轴心抗压强度增大，预应力空心板梁的抗爆性能并没有明显提升；当混凝土轴心抗压强度分别为50，55，60，65和80 MPa，时间为20 ms时空心板梁点的竖向位移分别为−5.84，−5.77，−5.74，−5.52和−5.65 cm，最大位移较最小值位移的增幅仅为5.8%；钢筋中点位移的增幅也很小。从图10(c)也可看出：各工况下竖向位移峰值曲线基本重合，梁底部的整体变形基本相同，这5种情况下混凝土损失的质量占梁体的总质量的比 例最小为4.02%，最大为4.14%，质量损失比也基本相同。

(a) 底部混凝土中点位移时程曲线；(b) 上部钢筋中点位移时程曲线；(c) 空心板梁竖向位移峰值分布图

(a) 底部混凝土中点位移时程曲线；(b) 上部钢筋中点位移时程曲线；(c) 空心板梁竖向位移峰值分布图

人们通常认为混凝土轴心抗压强度越高，其各方面性能应相应提高，但田力等[10]在研究刚性球撞击不同混凝土强度的柱时发现：低强度材料对应变率效应更加敏感，当应变率不同时，低强度混凝土的DIF (dynamic increase factor)可能会比高强度混凝土的DIF高几倍，此时，低轴心抗压强度的混凝土实际上具有高动力抗压强度，有可能出现在冲击波和破片复合作用下，随着混凝土强度提升，预应力空心板梁的抗爆性能并无明显提升的现象。此外，在炸药驱动下，破片速度高达2 100 m/s，对梁的击穿作用非常明显。田力等[7]在研究炸药和破片复合作用下钢柱的动力响应时也得出了类似的结论，当材料达到一定强度时，再提升构件的强度，并不能明显提高其抗爆性能。所以，在实际生产和生活中，应合理选择混凝土材料的强度，一味追求高强度，并不能明显提升构件的抗爆性能。

4.4 普通纵向钢筋配筋率对空心板梁动力响应的影响

分别模拟纵筋配筋率为0.006，0.009，0.012，0.015和0.018时爆炸波与破片复合作用下预应力空心板梁的破坏情况。纵筋的配筋率通过改变钢筋直径的方法来实现，其他参数保持不变。

图11所示为不同纵筋配筋率下空心板梁的位移曲线。从图11可以看出：随着纵筋配筋率的增加，结构的抗爆性能有一定提升，但当纵筋配筋率增大到一定程度后，其抗爆性能又会出现降低的情况。例如，当纵筋配筋率为0.006，0.009，0.012，0.015和0.018，20 ms时，预应力空心板梁点的位移分别为−5.84，−5.41，−5.18，−6.30和−6.06 cm；纵筋配筋率从0.006增大到0.012，位移减少12.74%，但随着配筋率的增加，点的竖向位移反而增大。这是因为，配筋率的增加是通过改变钢筋直径的方法来实现的，随着钢筋直径增大，破片打碎混凝土之后与钢筋发生接触的可能性增大，破片侵彻钢筋，使得预应力空心板梁的上部纵向钢筋发生断裂，如图12所示。钢筋的断裂加剧了受损伤构件的破坏，使得其抗爆性能降低。因此，在实际的生产生活中，预应力混凝土构件应选取适当的配筋率和钢筋直径，以提高构件的抗爆性能。

4.5 箍筋间距对空心板梁动力响应的影响

分别模拟箍筋间距为150，200，250和300 mm时爆炸波与破片复合作用下预应力空心板梁的破坏情况，其他参数保持不变。

图13所示为不同箍筋间距下空心板梁位移图。从图13可以看出：随着箍筋间距的增大，构件的抗爆性能逐渐减弱，但其减弱的趋势并非是呈线性的。例如，空心板梁底部混凝土中点位移在20 ms时分别为−5.80，−8.18，−8.52和−10.10 cm，箍筋间距从150 mm增加到200 mm，其中点竖向位移增加41.03%，质量损失比也从4.14%增加到7.19%；而箍筋间距从200 mm增大到250 mm时，无论从竖向位移的时程曲线还是从竖向位移峰值图来看，空心板梁抗爆性能基本一致，质量损失比也基本相同；而当箍筋间距从250 mm增大到300 mm时，中点竖向位移增加18.54%。这是由于随着箍筋间距的增大，箍筋对纵向钢筋及梁体的“套箍”作用减弱，而这种“套箍”作用的减弱并非是线性的。综上所述，相比纵筋配筋率，箍筋对构件抗爆性能的影响更大一些，所以，在实际的生产生活中需选择合理的配箍间距，以提高构件的抗爆性能。

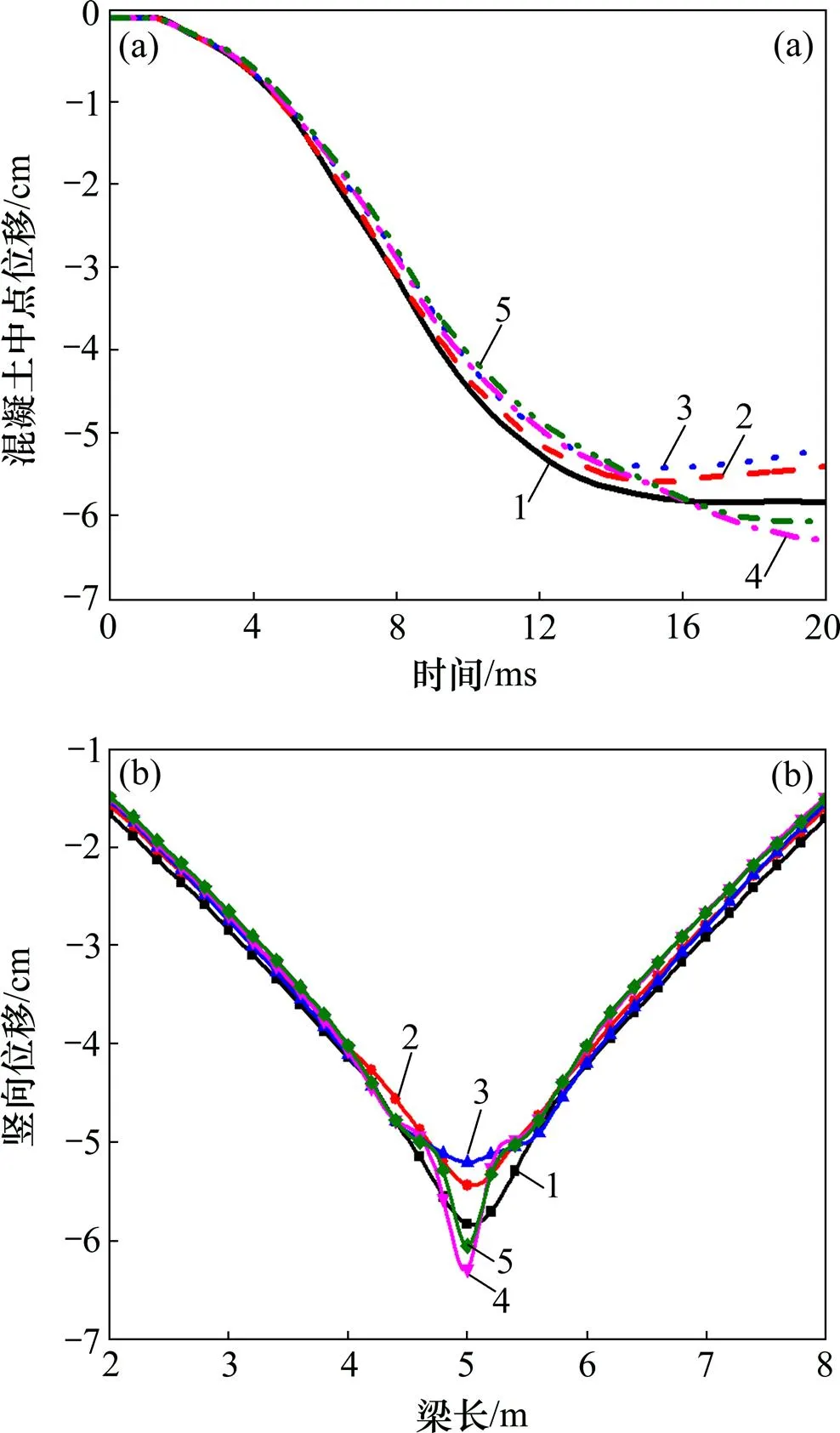
(a) 底部混凝土中点位移时程曲线；(b) 空心板梁竖向位移峰值分布图

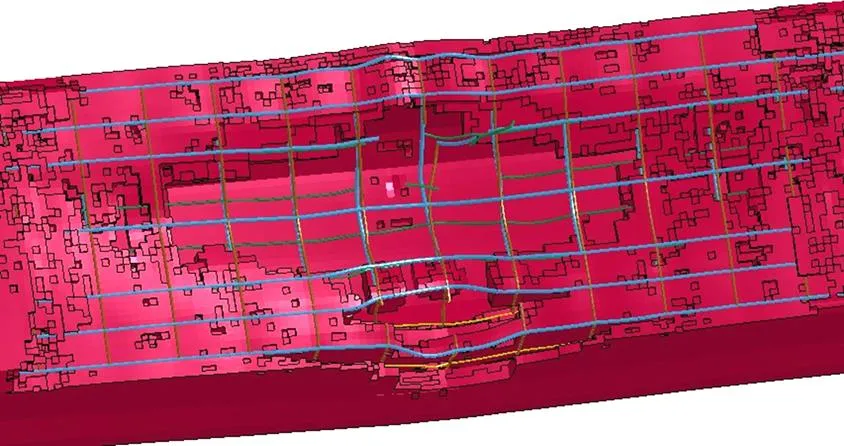
图12 钢筋断裂示意图

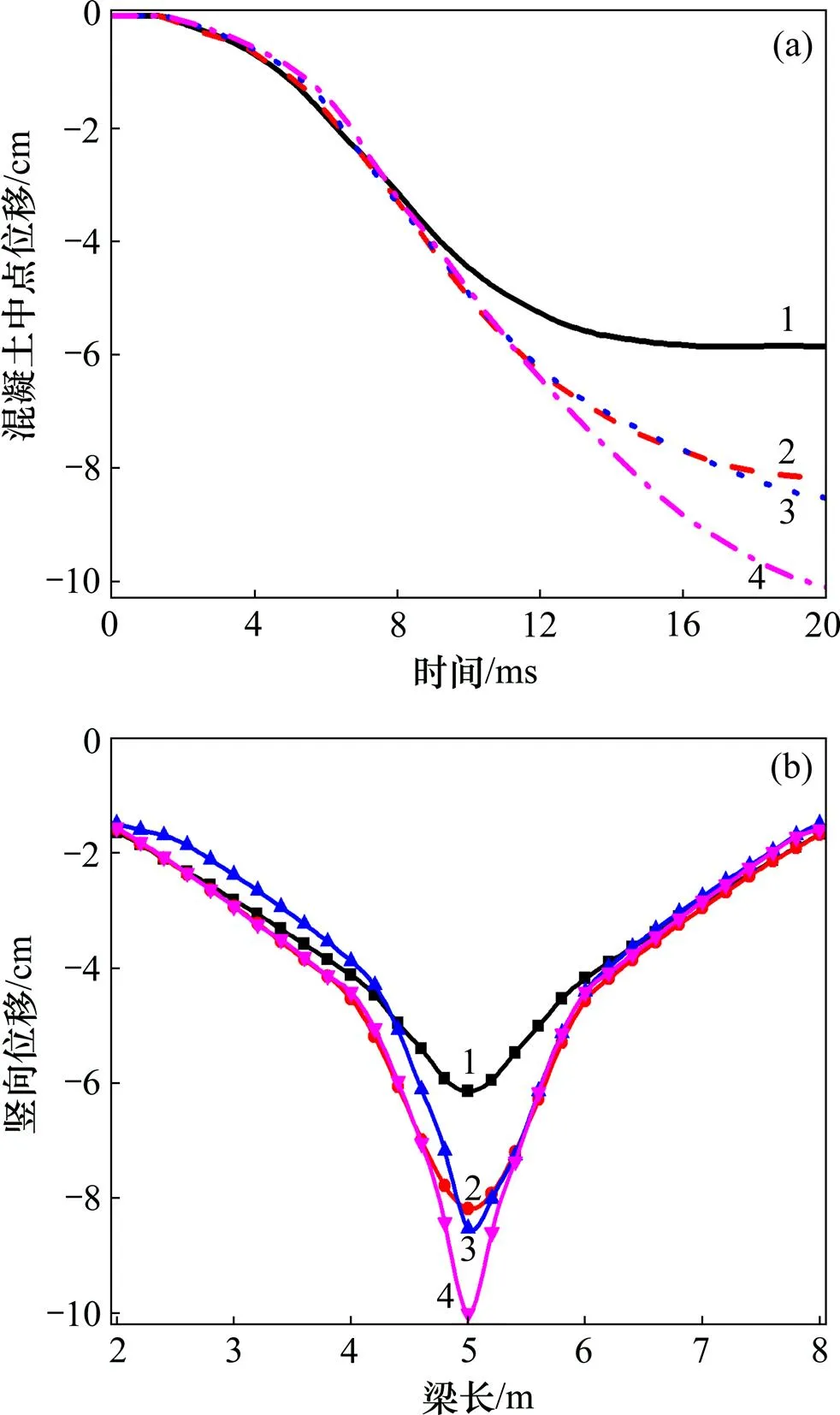
(a) 底部混凝土中点位移时程曲线；(b) 空心板梁竖向位移峰值分布图

箍筋间距/mm：1—150；2—200；3—250；4—300。

图13 不同箍筋间距下空心板梁位移曲线

Fig. 13 Displacement curves of hollow beam under different stirrup spacings

5 结论

1) 通过模拟预应力混凝土板在近爆冲击波作用下的动力响应及炸药驱动预制破片的试验，其结果证明了本文中所用材料本构模型及技术路线的合理性与可靠性。

2) 在近距离爆炸作用下，当有破片存在时结构往往会发生较明显的局部破坏，这对结构的抗爆性能是不利的。因此，在抗爆设计中，应当考虑破片的局部穿甲效应。

3) 预应力空心板梁的张拉控制应力越大，其抗爆性能越好；当张拉控制应力取为最常见的0.75ptk时，即使空心板梁有不同程度的应力损失，其抗爆性能也基本相同；混凝土强度的提升对构件的抗爆性能的提升作用不大；普通纵向钢筋的配筋率在一定范围可使对构件的抗爆性能有小幅度提升；随着箍筋间距增大，构件的抗爆性能明显减弱。

[1] 李砚召, 王肖钧, 张新乐, 等. 预应力混凝土结构的抗爆性能试验研究[J]. 实验力学, 2005, 20(2): 179−185. LI Yanzhao, WANG Xiaojun, ZHANG Xinle, et al. Experimental study on anti-explosion performance of prestressed concretes structures[J]. Experimental Mechanics, 2005, 20(2): 179−185.

[2] CHOI J H, CHOI S J, CHO C M, et al. Experimental evaluation of Bi-directionally unbonded prestressed concrete panel blast resistance behavior under blast loading scenario[J]. Journal of the Korea Concrete Institute, 2016, 28(6): 673−683.

[3] CHEN Wensu, HAO Hong, CHEN Shuyang. Numerical analysis of prestressed reinforced concrete beam subjected to blast loading[J]. Materials and Design, 2015, 65: 662−674.

[4] 刘超. 预应力混凝土桥粱爆炸荷载作用效应研究[D].武汉: 武汉理工大学交通学院, 2012: 77−97. LIU Chao. The study of the effects of blast loading on prestressed concrete bridge[D]. Wuhan: Wuhan University of Technology. College of Transportation, 2012: 77−97.

[5] 夏小虎. 预应力钢筋混凝土梁在爆轰条件下的动力行为研究[D]. 武汉: 武汉理工大学土木工程与建筑学院, 2012: 31−43. XIA Xiaohu. Dynamic behavior of prestressed reinforced concrete beam under detonation condition[D]. Wuhan: Wuhan University of Technology. College of Civil Engineering and Architecture, 2012: 31−43.

[6] 田力, 朱运华. 冲击波和破片联合作用下RC柱的损伤分析[J]. 建筑科学与工程学报, 2017, 34(2): 64−70. TIAN Li, ZHU Yunhua. Damage analysis of RC column under combined action of shock wave and fragments [J]. Journal of Building Science and Engineering, 2017, 34(2): 64−70.

[7] 田力, 张浩. 冲击波和预制破片复合作用下Ｈ型钢柱损伤效应分析[J]. 同济大学学报(自然科学版), 2018, 46(3): 289−299. TIAN Li, ZHANG Hao. Damage effects analysis of H-section steel column subjected to synergistic effects of blast and fragments[J]. Journal of Tongji University (Natural Science), 2018, 46(3): 289−299.

[8] DAVID G, WINGET P E, ASCE M, et al. Analysis and design of critical bridges subjected to blast loads [J]. Journal of Structural Engineering, 2005, 131(8): 1243−1255.

[9] CHUNG KIM YUEN S, LANGDON G S, NURICK GN, et al. Response of V-shape plates to localized blast load Experiments and numerical simulation[J]. International Journal of Impact Engineering, 2012, 46: 97−109.

[10] 田力, 朱聪, 王浩, 等. 碰撞冲击荷载作用下钢筋混凝土柱的动态响应及破坏模式[J]. 工程力学, 2013, 30(2): 150−155. TIAN Li, ZHU Cong, WANG Hao, et al. Dynamic response and failure mode of reinforced concrete columns under impact loading[J]. Engineering Mechanics, 2013, 30(2): 150−155.

[11] 王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007: 487−489. WANG Xinmin. ANSYS engineering structure numerical analysis[M]. Beijing: China Communications Press, 2007: 487−489.

[12] 张威, 肖正明, 伍星, 等. 基于动力松弛法的齿轮系统动态接触仿真分析[J]. 机械传动, 2015, 39(10): 108−113. ZHANG Wei, XIAO Zhengming, WU Xing, et al. Simulation analysis of dynamic contact of gear system based on dynamic relaxation method[J]. Mechanical Transmission, 2015, 39(10): 108−113.

[13] 师燕超. 爆炸荷载作用下钢筋混凝土结构的动态响应行为与损伤破坏机理[D]. 天津: 天津大学建筑工程学院, 2009: 61−63. SHI Yanchao. Dynamic response behavior and damage mechanism of reinforced concrete structures under explosive load[D]. Tianjin: Tianjin University. School of Civil Engineering, 2009: 61−63.

[14] 段新峰, 呈远胜, 张攀, 等. 爆炸波和破片复合作用下I型夹层板毁伤仿真[J]. 中国舰船研究, 2015, 10(6): 45−69. DAUN Xinfeng, CHENG Yuansheng, ZHANG Pan, et al. Damage simulation of Type I sandwich plate under shock wave and fragment joint action[J]. Journal of Ship Research, 2015, 10(6): 45−69.

[15] 印立魁, 蒋建伟, 门建兵, 等. 立方体预制破片战斗部破片初速计算模型[J]. 兵工学报, 2014, 35(12): 1967−1971. YIN Likui, JIANG Jianwei, MEN Jianbing, et al. Velocity calculation model of cubic prefabricated warhead fragment [J]. Journal of Ordnance, 2014, 35(12): 1967−1971.

[16] 王有志. 预应力混凝土结构[M]. 北京: 中国水利水电出版社, 1998: 25−26. WANG Youzhi. Prestressed concrete structure[M]. Beijing: China Water Conservancy and Hydropower Press, 1998: 25−26.

Analysis of damage effects of a prestressed reinforced concrete hollow beam subjected to the synergistic effects of blast and fragments

TIAN Li1, 2, LI Yongxin1

(1. School of Civil Engineering, Tianjin University, Tianjin 300072, China; 2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education, Tianjin University, Tianjin 300072, China)

Numerical analysis was carried out to research the damage situations of prestressed reinforced concrete hollow beams under the synergistic effects of blast and fragments. Finite element software ANSYS/LS-DYNA was used to simulate the blast test of the prestressed concrete panel and the experiment of explosive driving prefabricated fragments. The reliability of the material constitutive models and technical route used in this paper was verified. The differences in the dynamic response of the hollow beam under the influences of blast wave, fragment load and both of them were analyzed. At the same time, parametric studies were carried out to investigate the effects of tensile control stress, level of stress loss, concrete strength, reinforcement ratio, and spacing of stirrups on dynamic response of the prestressed concrete hollow beam. The results show that with the increase of tensile control stress, the anti-explosion performance of the hollow beam increases. The anti-explosion performance of hollow beam is basically the same at the same tension control stress level, even if there are different levels of stress loss. The improvement of concrete strength on the anti-explosion performance is not significant. The increase of the reinforcement ratio improves the anti-explosion performance of hollowbeam slightly within a certain range. With the increase of the spacing of stirrups, the anti-explosion performance of the component weakens obviously.

prestressed reinforced concrete hollow beam; blast; fragment; synergistic effects; parametric study

TU378.2

A

1672−7207(2019)05−1154−11

10.11817/j.issn.1672−7207.2019.05.019

2018−06−18；

2018−08−18

国家自然科学基金资助项目(50678116, 51178310) (Projects(50678116, 51178310) supported by the National Natural Science Foundation of China)

田力，博士，副教授，从事结构抗爆及防护技术研究；E-mail：ltian@tju.edu.cn

(编辑 伍锦花)