Reversible Data Hiding Based on Pixel-Value-Ordering and Pixel Block Merging Strategy

Wengui Su ,Xiang Wangand Yulong Shen

Abstract:With the reversible data hiding method based on pixel-value-ordering,data are embedded through the modification of the maximum and minimum values of a block.A significant relationship exists between the embedding performance and the block size.Traditional pixel-value-ordering methods utilize pixel blocks with a fixed size to embed data;the smaller the pixel blocks,greater is the embedding capacity.However,it tends to result in the deterioration of the quality of the marked image.Herein,a novel reversible data hiding method is proposed by incorporating a block merging strategy into Li et al.’s pixel-value-ordering method,which realizes the dynamic control of block size by considering the image texture.First,the cover image is divided into non-overlapping 2×2 pixel blocks.Subsequently,according to their complexity,similarity and thresholds,these blocks are employed for data embedding through the pixel-value-ordering method directly or after being emerged into 2×4,4×2,or 4×4 sized blocks.Hence,smaller blocks can be used in the smooth region to create a high embedding capacity and larger blocks in the texture region to maintain a high peak signal-to-noise ratio.Experimental results prove that the proposed method is superior to the other three advanced methods.It achieves a high embedding capacity while maintaining low distortion and improves the embedding performance of the pixel-value-ordering algorithm.

Keywords:Reversible data hiding,pixel-value-ordering,prediction error expansion,dynamic block partition.

1 Introduction

Reversible data hiding (RDH),also known as lossless data hiding,can recover both secret information and host image without loss after the extraction of embedded data [Caldelli,Filippini and Becarelli (2010)].Currently,RDH has been applied in quality sensitive fields such as copyright protection,medical image processing,and military image protection.

Based on lossless compression,early RDH methods realized reversible information embedding [Celik,Sharma,Tekalp et al.(2005)].The embedding capacity (EC)is highly limited,as only the compressed redundant space is utilized for embedding.To improve the embedding capacity and maintain a low distortion,many efficient RDH techniques have been introduced and developed over time.Among them,difference expansion (DE)[Tian (2003);Pei,Wang,Li et al.(2013)] and histogram shifting (HS)[Ni,Shi and Ansari (2006);Li,Li,Yang et al.(2013)] are two fruitful schemes.

The difference expansion scheme proposed by Tian [Tian (2003)] is a basic RDH technique.In recent years,the DE scheme has been extensively researched and developed in the aspects of integer transformation [Wang,Li,Yang et al.(2010)],reducing bitmap size [Hu,Lee and Li (2009)],prediction of error expansion (PEE)[Yao,Liu,Tang et al.(2018);He,Zhou,Cai et al.(2017)],and pixel-value-ordering (PVO)[Li,Li,Li et al.(2013);Ou,Li and Wang (2016)].

The HS algorithm proposed by Ni et al.[Ni,Shi and Ansari (2006)] is another important scheme for RDH.This scheme embeds secret information by shifting the intensity histogram bins between the peak point and zero point to obtain a higher quality embedded image.However,the maximum embedding capacity is limited by the number of pixels at the peak of the histogram.To improve the embedding capacity,many scholars have performed further improvements based on HS technology in recent years [Qin,Chang,Huang et al.(2013);Wang,Ye,Wang et al.(2018);Rad,Wong and Guo (2016);Du,Yin and Zhang (2018)].For example,Du et al.[Du,Yin and Zhang (2018)] introduced the HS-based method in JPEG bitstream to optimize histogram modification.This novel method achieves lossless embedding with high payload and less file size expansion in an identical payload.

Thodi et al.[Thodi and Rodriguez (2007)] proposed the PEE method by combining DE and HS.The PEE algorithm introduces HS to compress the location map efficiently and utilizes the prediction error instead of the adjacent pixel difference for expansion embedding.The local correlation of the larger neighborhood of the image rather than the two adjacent pixels is considered in the prediction;therefore,the PEE method achieves a tradeoff between embedding capacity and fidelity.Because the prediction accuracy has an important impact on the performance of the PEE method,many related PEE methods have also been presented for efficient predictions,such as the median edge detector (MED)[Thodi and Rodriguez (2007)],gradient adjusted prediction (GAP)[Wu and Memon (2015)],adaptive embedding [Cao,An,Yao et al.(2018)],rhombus prediction [Sachnev,Kim,Nam et al.(2009)],and pixel value ordering [Li,Li,Li et al.(2013)].In most of the improved PEE methods,both local complexity (LC)and prediction error (PE)can be served as metrics to determined block smoothness.The hypothesis that a direct proportion exists between LC and PE is typically exploited to reduce image distortion.However,in practice,some cases exist that do not conform to this hypothesis.Hence,Chen et al.[Chen,Ni,Hong et al.(2017)] devised a directionally enclosed prediction and expansion method to limit data embedding to pixels proportional to LC and PE.Experiments proved that this method yields high image fidelity while providing a considerable payload.

In recent years,the PVO-based RDH [Li,Li,Li et al.(2013)] has attracted increasing attention.The advantage of this method is that it can achieve better visual quality at low EC.In the PVO-based method [Li,Li,Li et al.(2013)],the image is divided into equal-sized pixel blocks;subsequently,the second largest/smallest pixel in the block is used to predict the largest/smallest pixel that is modified to embed data and reversibility is achieved by maintaining the order of pixel values within each block before and after embedding.Because the pixels in the same block are often highly correlated,the PVO-based RDH method presents an excellent embedding performance.Meanwhile,the block selection technique is adopted to select smooth blocks for data embedding and a more concentrated histogram is obtained that improves the embedding performance.However,bin0,which is typically the second-highest bin,was not used in Li et al.’s method [Li,Li,Li et al.(2013)].Peng et al.[Peng,Li and Yang (2014)] extended Li et al.’s work by introducing the relative position of the pixels into the prediction to construct a bilateral prediction error histogram.In his method,bin1 and bin0 were exploited for data embedding to better utilize image redundancy and achieve better embedding performance than that of Li et al.[Li,Li,Li et al.(2013)].The work of Weng et al.[Weng,Pan,Deng et al.(2018)] is an improvement of Peng et al.’s work [Peng,Li and Yang (2014)].They developed a novel pixel modification strategy.Three largest (or smallest)pixels in a smooth block were exploited for prediction;hence,a smooth block can carry at most 3log2bits.Furthermore,two-layer embedding and n block partition ways were combined to achieve high embedding capacity and low distortion.

To our knowledge,the PVO embedding performance has a significant correlation with block size;therefore,many RDH methods are dedicated to introducing the block selection strategy in PVO embedding.Wang et al.[Wang,Ding and Pei (2015)] further improved Peng et al.’s work [Peng,Li and Yang (2014)] and proposed a PVO-based method with a dynamic block strategy.In accordance with the block complexity,the pixel blocks are divided into rough blocks,normal blocks,and flat blocks.Subsequently,the rough blocks are excluded from data embedding,whereas the flat blocks are further divided into four sub-blocks to increase the embedding capacity.A larger block size is selected in the texture area to ensure high peak signal-to-noise-ratio (PSNR),while a smaller block size is adopted in the smoothing area to achieve higher EC.This method can provide higher embedding capacity and lower distortion than the PVO-based RDH algorithm proposed in Li et al.[Li,Li,Li et al.(2013)] and [Peng,Li and Yang (2014)].Further,Weng et al.[Weng,Liu,Pan et al.(2016)] proposed a reversible data hiding method based on flexible block-partition and the adaptive pixel modification strategy.The image is partitioned in accordance with the local complexity metric,and a high-correlation block is further divided into sub-blocks of size 1×3,and each block can be embedded with two data bits.A moderate-correlation block is divided into two sub-blocks of different sizes,each of which can embed up to four data bits.A low-correlation block can embed up to two bits.This method outperforms some of the state-of-the-art methods.Based on the dynamic block strategy proposed by Wang et al.[Wang,Ding and Pei (2015)];He et al.[He,Cai,Zhou et al.(2017)] developed a multistage blocking strategy for n-threshold and n-level blocks.The image was first divided into non-overlapping root blocks.The root blocks were further divided into intermediate blocks or leaf blocks in accordance with the threshold.Further,different embedding schemes were selected in accordance with the block type.The algorithm guarantees less embedding distortion under the given EC,and outperforms Wang et al.’s work in computational complexity.Meikap et al.[Meikap and Jana (2018)] developed a PVO-based method with varying block sizes and multi-direction overlapping embedding.In this method,a parameterαwas utilized to maintain the order of pixel in a block to ensure that the method is suitable for different block sizes.Three directions:horizontal,vertical,and diagonal of each block were embedded for high embedding capacity.Experiments indicate that the method yields a better performance.

To achieve larger embedding capacity and high fidelity,many improved PVO-based methods aim to exploit the pixel correlation to obtain more suitable pixel block for data hiding.Inspired by this,a novel PVO-based algorithm based on the block merging strategy is proposed herein.In Li et al.’s work [Li,Li,Li et al.(2013)],the cover image was divided into blocks of equal size and the pixels in each block were sorted in accordance with the pixel values;subsequently,data embedding was realized by modifying the maximum and minimum values of each block.For a given EC,blocks of different sizes,i.e.,n1×n2，n1,n2∈{2,3,4,5}were tested in the embedding process;subsequently,that with the best embedding performance was determined to be the final block size.A larger block produces a more concentrated histogram that improves the image PSNR but reduces the EC significantly.A smaller block helps to achieve higher EC,but typically results in the deterioration in image quality.The PVO-based embedding performance has a significant correlation with the block size and is highly limited by the uniform-blocking manner.To achieve high embedding capacity while preserving good visual quality,we propose a pixel block merging strategy based on the local complexity,similarity,and thresholds.We first divide the image into non-overlapping 2×2 blocks;subsequently,these pixel blocks are employed for PVO-based embedding or after being merged,which is decided according to a local complexity measurement.Experimental results indicate that the proposed method exploits the advantage of pixel correlation well and yields high embedding capacity without deteriorating the image quality.

The remainder of this paper is structured as follows.Section 2 provides an introduction of Li et al.’s PVO-based RDH algorithms.Section 3 introduces the proposed PVO-based embedding and extraction procedures in detail.Section 4 provides the experimental results and Section 5 concludes this paper.

2 Related works

Li et al.’s method [Li,Li,Li et al.(2013)] fully utilizes the similarity of pixels and can create the space for data embedding by modifying the maximum and minimum pixel blocks,thus enabling sufficient payloads to be embedded into images with low distortion.Take the maximum-modification-based embedding phases as an example.First,divide the cover image into non-overlapping and equal-sized blocks.For a given block includingnpixelsX={x1,x2,...,xn},sort the pixel values (x1,x2,...,xn)in the ascending order,and obtain a sequence (xσ(1),...,xσ(n)),whereσ:(1,2,...,n)→(1,2,...,n)denotes the unique one-to-one mapping such thatxσ(1)≤xσ(2)≤...≤xσ(n),σ(i)＜σ(j)ifxσ(i)=xσ(j)andi＜j,subsequently,the second largest value)1(-nxσcan be used for predicting the maximumxσ(n),and the corresponding prediction error can be expressed as follows:

A histogram forPEmaxcan be obtained after calculating the prediction errors of all blocks.

The value ofPEmaxis always positive and bin1 (the bin ofPEmax=1)is typically the peak value of the histogram,implying that this bin can be regarded as the interior region for data embedding.Furthermore,to ensure reversibility,bins larger than 1 are used as the external regions and are shifted to create the space for data embedding.Therefore,the maximum)(nxσcan be modified as follows:

where b∈{0,1} refers to the data to be embedded.

Let the marked value ofXbe represented as (y1,...,yn),and sort its values in the ascending order and obtain (yσ(1),...,yσ(n)).Subsequently,all i ≠σ(n)satisfies the condition thatyi=xiand=yσ(n).In addition,the order of pixel values is consistent in the embedding process,implying that the mapping ofσremains unchanged before and after data embedding.

When decoding,the prediction error can be described as follows:

Only when∈{1,2}caninclude the embedded data,and the process of decoding is detailed as follows:

(1)If∈{1,2},the embedded data will beb=-1 and the original value will

3 Proposed method

In the PVO-based RDH scheme [Li,Li,Li et al.(2013);Peng,Li and Yang (2014)],the image will be divided into pixel blocks of equal size,which subsequently are utilized for data embedding in a block-by-block manner.As shown in Fig.1,the larger blocks lead to higher PSNR for low EC,whereas the smaller blocks yield a better embedding performance for high EC.Moreover,the block size is related to the maximum EC.The smaller blocks can provide higher EC.For PVO-based works,the tradeoff between capacity and fidelity is achieved by adjusting the block size.

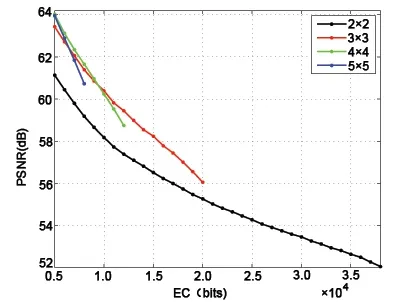
Figure 1:Performance of the scheme proposed by Peng et al.[Peng,Li and Yang (2014)] with different block sizes for the image Lena

With the above consideration,a novel PVO-based RDH using the block merging strategy is proposed to better exploit the pixel correlation within a block and create more embedded space with low distortion.In the smooth region where the pixels exhibit similar pixel values and good prediction accuracy,a smaller block size is adopted to improve the EC.Meanwhile,in the texture region where the pixels exhibit a weak correlation,a larger block size is employed to preserve good visual quality.

First,the host image is divided into non-overlapping 2×2 pixel blocks,and are classified into smooth blocks or normal blocks according to the local complexity measurement.The smooth 2×2 pixel blocks are directly embedded via the PVO-based method [Li,Li,Li et al.(2013)].For normal pixel blocks,the similarity of the adjacent blocks is measured;subsequently,the similar blocks are merged into larger 2×4 or 4×2 blocks to perform PVO-based embedding.The unused merged blocks are further merged into 4×4 pixel blocks in accordance with the similarity and thresholds for PVO-based embedding.Hence,the proposed method achieves the dynamic control of the block sizes according to the image texture possible and achieves a better payload with lower distortions.

3.1 Classification of pixel blocks

3.1.1 Definition of complexity

In this study,we utilized the block complexity (denoted byNL)to differentiate a blockIiin the smooth region from the others.For the blocks with different texture complexities,different sizes of the embedding blocks should be determined.The image blocks can be classified by theNLand thresholdT.Smooth blocks can be embedded via the PVO-based method directly,while ordinary blocks should be embedded via block merging before embedding.

Suppose the cover imageIis a grayscale image of sizeHW× ;divideIintonr×cnon-overlapping blocks,whereI={I1,I2,...,In}.Sort a blockIiby its pixel values in the ascending order to obtainIi=(x1,x2,...,xk),wherex1≤x2≤...≤xk.Thus,the block complexityNLiofIican be defined as follows:

3.1.2 Smoothness classification

For a one-pixel blockIi(i=1,2,…,n)ofI,Eq.(4)can be used for calculating the local complexityNLi(i=1,...,n).Further,whether a pixel block is smooth can be determined using the thresholdTj(j=1,2,3,-1≤Tj≤255).All pixel blocks can be divided into two sets,EandG,according to their local complexitiesNLiand thresholdsTj.SetEcontains all smooth blocks that are employed to embed data.The setGcontains ordinary blocks that cannot be embedded into the data directly but must be further merged to maintain low distortion according to the similarity.The detailed steps of the block merging strategy are described in Section 3.2.2.As for the classification of the pixel blocks,two cases exist:

Case 1:ifNLi≤Tj,the blockIiis classified as a smooth block and added to setE.In this case,Iilocates in the smooth region where the blocks have similar pixel values and can be used for embedding.According to the PVO-based method in Li et al.[Li,Li,Li et al.(2013)],two bits of data (one bit for maximum and one bit for minimum)are directly embedded into blockIi.

Case 2:ifNLi＞Tj,Iiis denoted as a normal block.In this case,Iilikely locates in the texture region where using a larger block size will exhibit evident advantages and higher PSNR.Therefore,the normal blockIiis added sequentially into setGand labeled withGi(i=1,...,l)for further processing in Section 3.2.

Reversibility is guaranteed by maintaining the complexityNLof each block invariant after embedding.In the embedding process of the PVO-based method,the pixels of a normal block remain unchanged;thus,the complexity remains unchanged as well.Meanwhile,for the smooth block,only the maximumkxand minimum1xare modified to accomplish the PVO-based embedding.In such situations,the pixel values (x2,x3...,xk-1)remain unchanged.Therefore,the complexity of a smooth block remains unchanged according to Eq.(4).

3.2 Pixel merging strategy

3.2.1 Definition of the similarity between blocks

After completing the block classification,adjacent blocks with high similarity in setGwill be merged to create a larger block before performing data embedding to maintain higher PSNR and further improve the performance of the PVO-based method.

For two adjacent non-overlapping pixel blocksGi=(x1,x2,...,xk)andGi+1=(y1,y2,...,yk)(i=1,2,...,l-1)of sizer×cinG,the definition of similarity (denoted bySim)between blocks is:

The thresholdSis used to measure the similarity of two blocks.IfSSimi≤,Giis similar toGi+1,and these two blocks can be merged into a larger block with the size ofr×2cor2r×c.Similar to the local complexityNL,the similaritySimremains unchanged during embedding and extraction,thus ensuring reversibility.

3.2.2 Pixel merging strategy

Specifically,we use a thresholdSto estimate the similarity of two adjacent blocks in the setG.According to the similaritySimof two r×c blocksGiandGi+1(i=1,2,...,l-1)and the thresholdS,two situations must be considered.

Case 1:IfSSimi≤,Gihas high correlation withGi+1,merge these two r×c blocks to form a new pixel block of size of r×2c or 2r×c.After this process,the better correlation among the pixels within the merged block will be maintained to ensure better visual effects in the texture regions after embedding.Subsequently,the block classification method depicted in Section 3.1.2 is applied again to estimate the smoothing level of the new merged block to determine whether the new pixel block should be embedded or further merged.

Case 2:IfSSimi＞,a significant difference appears between the pixel blocksGiandGi+1,and will lead to severe distortions and thus not suitable for embedding.

3.3 Embedding procedure

In this section,the embedding procedure of the presented method will be described in detail.Here are the specific steps.

Step 1:image partition

Divide the host grayscale imageIinto n non-overlapping pixel blocks of size 2×2,I={I1,I2,...,In}.For each blockIi,sort its pixel values in the ascending order as {x1,x2,...,x4},such thatx1≤x2≤...≤x4.

Step 2:location map (LM)construction

For pixel values (x1,x2,...,x4)in each blockIi,if max(x1,x2,...,x4)=255or min(x1,,x2,...,xn)=0,then this block may cause an overflow or underflow and should be excluded from embedding.In this case,we set the location mapLM(j)=1,otherwiseLM(j)=0.Therefore,LMis a binary sequence of lengthξ.LMis consequently compressed losslessly using arithmetic coding and the length ofLMis denoted aslclm.

Step 3:block Classification and Embedding

Each blockIishould be classified according to the method in Section 3.1 with the given thresholdT1.

● IfLM(i)=1,then the block is an exception that will cause overflow/underflow;skip this block and add it into setC.

● IfLM(i)=0 and1TNLi≤,then the block is smooth.Subsequently,addIito set E with labelEi(i=1,..,p).Subsequently,utilize the PVO-based method in Li et al.[Li,Li,Li et al.(2013)] to embed two bits into each block.

● IfLM(i)=0 andNLi＞T1,then the block is normal.Subsequently,add the pixel blockIiin sequence to setG(Gj(j=1,...,l).

Step 4:the first merging and embedding process

With the given thresholdSand the similaritySimiof adjacent blocksGjandGj+1inG,the first merging and embedding procedure are performed in this step.

1.IfSimi≤ S,subsequently mergeGiandGi+1into a larger pixel block of size 2×4 or 4×2.Subsequently,re-estimate the block complexity of the merged block with the given thresholdT2and the method described in Step 3.If smooth,the merged block is added to setE(Ei(i=p+1,...,q))for embedding data.Further,two bits of data should be embedded into each of the smooth blocks.If normal,the merged block is grouped into a setM,whereMk=Gj∪Gj+1(k=1,2,...,n ;j=1,2,...,l-1)for the second merging process.

2.IfSimi＞ S,neither blockGjnorGj+1is used for merging and embedding.Subsequently,add these two blocks into set C.

Step 5:the second merging and embedding process

The second merging is performed in setMusing the same steps in Step 4 and the thresholdT3.All the smooth blocks generated in this step are added into setE(Ei(I=q+1,...,endξ )and the remaining blocks in setC.For every smooth block,two bits of data are embedded.Repeat this step until all embeddable blocks are embedded and denote the index of the last data-carrying block asendξ.

The three threshold valuesT1,T2,T3,and the similarity thresholdSare related to specific images and the embedding capacity.Test all combinations;subsequently,the optimal threshold for different capacities can be determined.

Step 6:auxiliary information and the embedding procedure

Record the least-significant-bit (LSB)of the firstpixels of the image to generate a binary sequenceSLSB,which will be embedded into the image as part of the watermark.Subsequently,these LSBs are replaced by the following auxiliary information and the compressed location mapLM:

·ThresholdsT1(8 bits),T2(8 bits),andT3(8 bits)for block complexity;

·ThresholdsS(8 bits)for similarity;

·The length of the compressed location map

·The location map (ldmbits).

Finally,the sequenceSLSBis embedded into the remaining blocks {Eξend+1,...,Eξ} using the same method in Step 3 to generate the marked image.A flow chart of the embedding procedure is shown in Fig.2.

Figure 2:Embedding procedure

3.4 Extraction procedure

The extraction procedure is an inverse process of embedding.The detailed procedure consists of the following four steps.

Step 1:auxiliary information and location map extraction

Record the LSB of the firstpixels of the marked image to extract the auxiliary information includingT1,T2,T3,S,endξ,andlclm.Subsequently,read the LSB of the latterlclmpixels to extract the compressed LM.The LM is recovered through the decompression of the compressed map.

Step 2:image partition and the preprocessing

Using the same method as Step 1 in Section 3.3,partition the marked image 'Iinto non-overlapping 2×2 blocks.Following the block classification and merging methods depicted in Section 3.3,Steps 3-5,and group all the blocks into setsEandC.

Step 3:sequenceSLSBextraction and image restoration

Extract the sequenceSLSBdefined in Section 3.3,Step 6,from the block sequence{Eξend+1,...,Eξ}using the PVO-based decoding method depicted in Section 2 and perform image restoration.

Step 4:data extraction and image restoration

Replace the LSB of the firstimage pixels by the sequenceSLSBextracted in Step 3.Extract the hidden data and recover the host image from blocks {E1,...,Eξend}using the method depicted in Step 3.For each block in setC,no data is hidden and its pixels remain unchanged.Thus,both the host image and secret data are fully recovered.

4 Experimental results

We first consider the determination of thresholds and the impact of the location map size to the embedding performance.The determination of thresholdsT1,T2,T3,andSdepends on the given EC and the host image,and no direction relationship exists between these thresholds.The best combination of these thresholds is determined iteratively to be the smallest values such that minimal image distortion can be achieved.

To enable a lossless reconstruction of the host image at the decoder,the location map must record the positions of the expandable differences.The location map is compressed losslessly and subsequently embedded into the carrier along with the payload.Despite the compression,the location map still occupies part of the embedding capacity.Hence,the size of the location map will affect the embedding performance to some extent.To minimize the impact of location map on the embedding performance,adaptive block partition is adopted in our method.Smaller blocks are exploited for smooth areas and larger blocks for texture areas,thus improving the distribution of 0 and 1 in the location map and further reducing the size of the compressed location map.From Tab.1,it is clear that the sizes of the LMs of different images have relatively small magnitudes compared with the EC;therefore,the LM has less influence on the embedding performance.

Table 1:The sizes of the LMs of different images

The proposed method was implemented in MATLAB.For the performance evaluation,three state-of-the-art RDH methods,namely,those of Li et al.[Li,Li,Li et al.(2013)],Peng et al.[Peng,Li and Yang (2014)],and Sachnev et al.[Sachnev,Kim,Nam et al.(2009)],were re-implemented and compared to the proposed method.The embedding performance was evaluated by comparing with other RDH schemes from two perspectives:visual image quality and embedding capacity.Eight grayscale images including Airplane,Elaine,Barbara,Baboon,Boat,Lake,Lena,and Peppers served as test images.Except Barbara,all images were downloaded from the USC-SIPI image database.

Li et al.’s work [Li,Li,Li et al.(2013)] is a high-fidelity PVO-based RDH method.Our method is a direct improvement of their work.Fig.3 shows that the embedding performance of our method is significantly better than that of Li et al.’s work for all test images.Referring to Tab.2 and Tab.3,the performance of the proposed method improves by 0.83 dB on average for an EC of 10,000 bits and by 0.83 dB for an EC of 20,000 bits compared to the performance of Li et al.’s work.In particular,for the smooth image of Airplane,the proposed method provides higher maximum EC (0.198 bit per pixel)than that of Li et al.[Li,Li,Li et al.(2013)] (0.145 bits per pixel).Moreover,the proposed method obtains a greater gain in PSNR for the large capacity cases.In this case,because the EC is high,the 2×2 blocks that are applied in Li et al.[Li,Li,Li et al.(2013)] cannot fully utilize the pixel correlation.In addition,because there are no sufficient smooth blocks at the high EC,the method proposed in [Li,Li,Li et al.(2013)] employed necessary rough blocks for data embedding that will result in image deterioration.However,with the proposed method,a high EC can be achieved using 2×2 blocks in the smooth regions.If the EC increases and there are no sufficient smooth blocks,the small blocks can be merged into 2×4,4×2,or 4×4 pixel blocks to obtain a smaller prediction error and maintain higher PSNR.

Peng et al.’s scheme [Peng,Li and Yang (2014)] is an extension of Li et al.’s work.In their work,bin0 was introduced into the embedding scheme and larger blocks were utilized to guarantee sufficient EC.Peng et al.’s scheme achieved a better performance than the PVO-based scheme [Li,Li,Li et al.(2013)].According to Fig.3,the proposed method achieves a substantial improvement in PSNR for every image regardless of the EC.Considering the results in Tab.2 and Tab.3,the PSNR improves by utilizing the proposed method when the capacities of the 10,000 bits and 20,000 bits are 0.29 dB and 0.36 dB,respectively.The maximum EC of the proposed method is almost the same as that of Peng et al.’s scheme.For a relatively large EC,the proposed method produces higher PSNR.The reason is that the capacity-dependent block strategies [Peng,Li and Yang (2014)] tend to use smaller blocks such as 2×2 or 3×3 when increasing the EC.Hence,it derives PNSR decreases,whereas a merging strategy is adopted in the proposed method to better exploit the correlations within a block and yields greater gain in the PSNR for the large capacity cases.

Sachnev et al.’s scheme [Sachnev,Kim,Nam et al.(2009)] is well known for its highly accurate prediction and has been verified better than many state-of-the-art works.As shown in Fig.3,the proposed method outperforms Sachnev et al.’s in most cases,except when the EC approaches its maximum (e.g.,9300 bits for Baboon,48000 bits for Airplane,and 29000 bits for Barbara).This is because the numbers of rough blocks have to be employed when aiming for maximum EC.However,the proposed scheme achieves superiority over Sachnev et al.’s scheme for a moderate EC.From Tab.2 and Tab.3,it is clear that the proposed scheme improves Sachnev et al.’s by 2.25 dB on average for an EC of 10000 bits and 1.74 dB for an EC of 20000 bits.

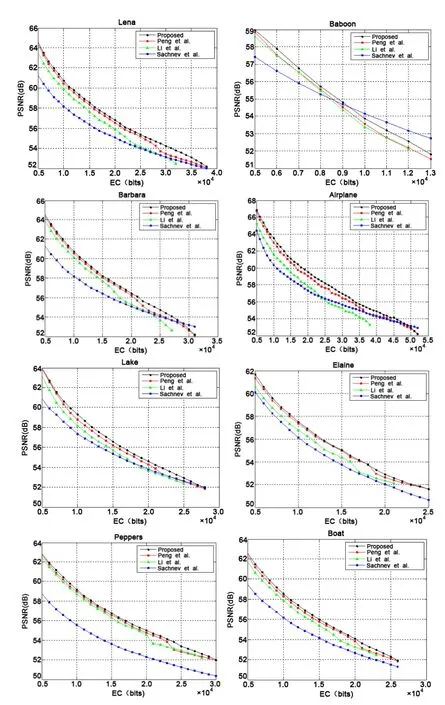
Figure 3:Performance comparison between the proposed method and the three methods of Sachnev et al.[Sachnev,Kim,Nam et al.(2009)],Li et al.[Li,Li,Li et al.(2013)],and Peng et al.[Peng,Li and Yang (2014)]

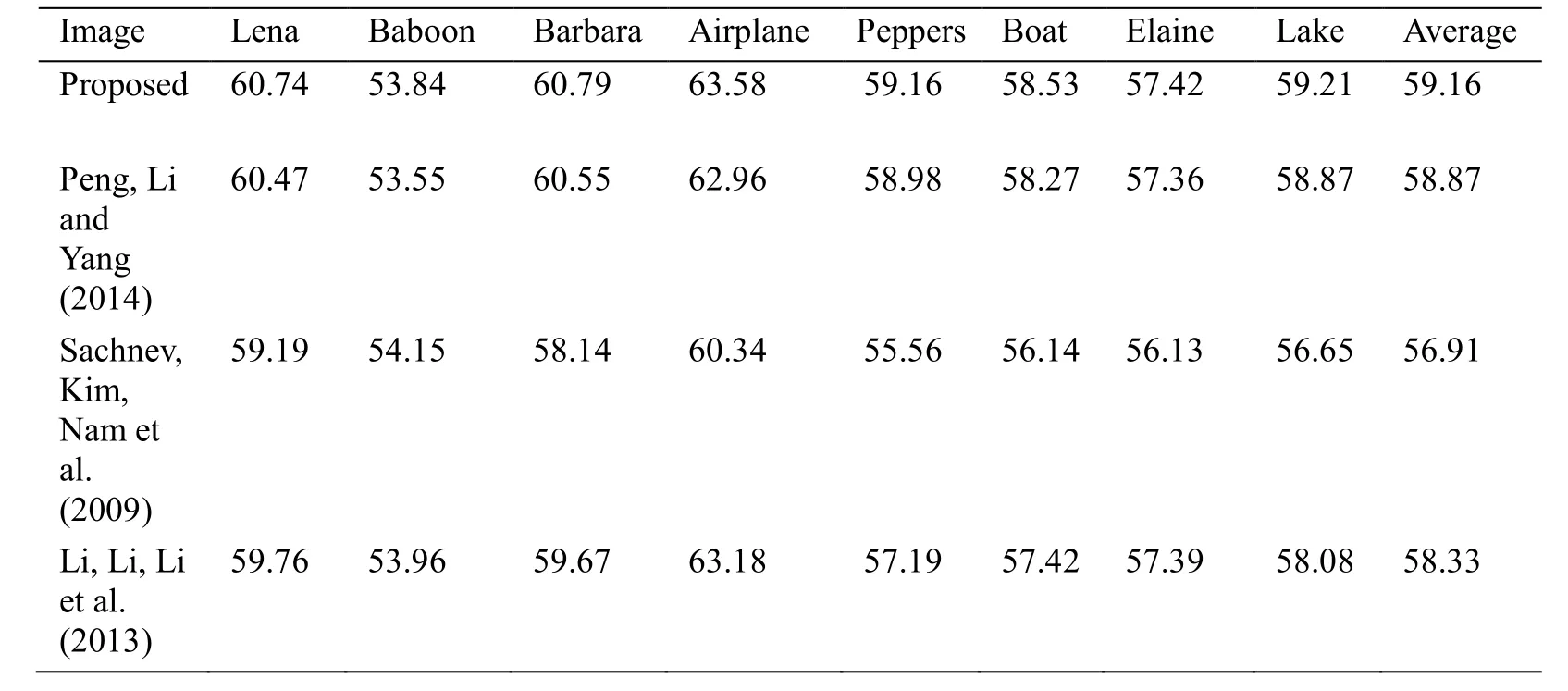
Table 2:Comparison of PSNR (in dB)between the methods of Peng et al.[Peng,Li and Yang (2014)],Sachnev et al.[Sachnev,Kim,Nam et al.(2009)],and Li et al.[Li,Li,Li et al.(2013)],and the proposed approach for an EC of 10,000 bits

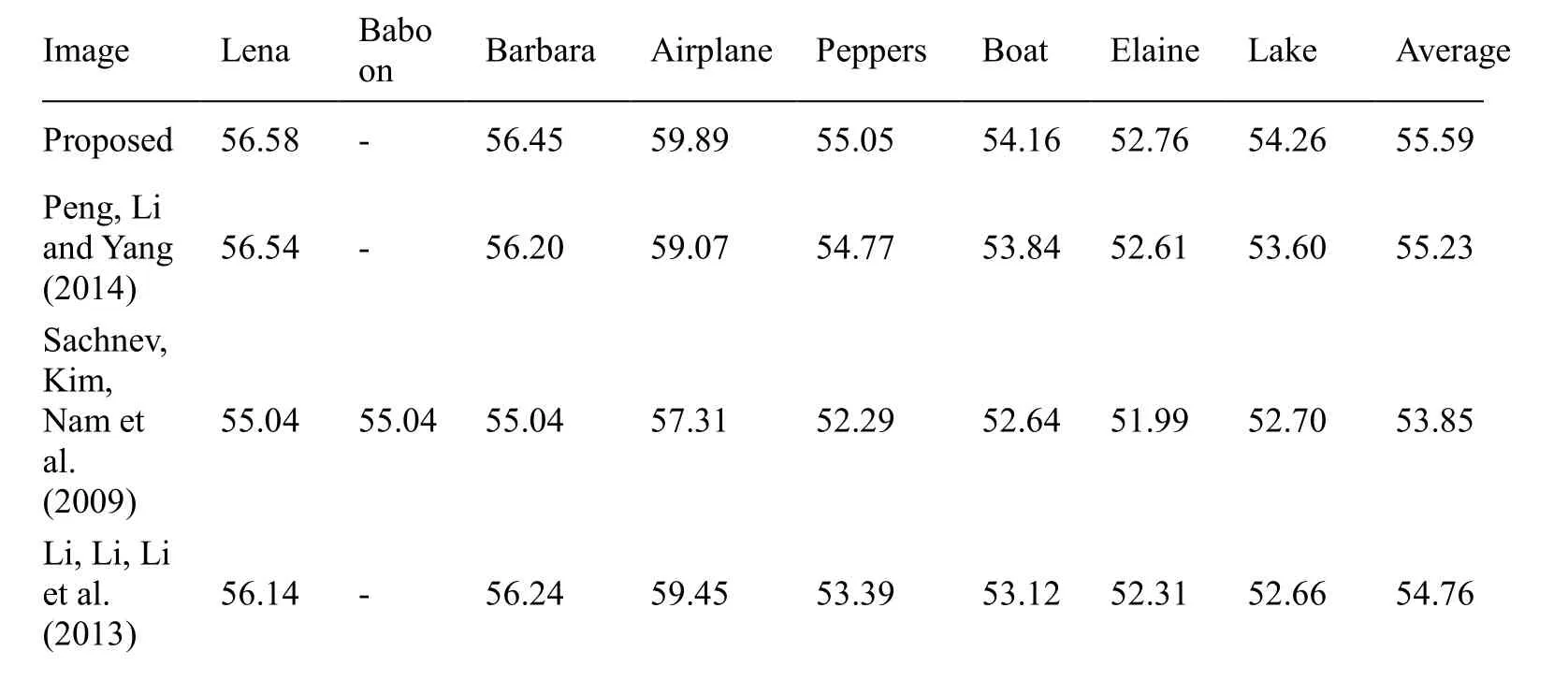
Table 3:Comparison of PSNR (in dB)between the methods of Peng et al.[Peng,Li and Yang (2014)],Sachnev et al.[Sachnev,Kim,Nam et al.(2009)],and Li et al.[Li,Li,Li et al.(2013)],and the proposed approach for an EC of 20,000 bits,for a capacity of 20,000 bits.The results for Baboon are eliminated herein because the proposed methods of Peng et al.and Li et al.cannot achieve such a payload

5 Conclusion

A reversible data hiding method that combined the PVO-based method with the block merging strategy was presented.Instead of uniform blocks,2×2 blocks were adopted in smooth regions while 2×4,4×2,or 4×4 blocks were employed in the rough regions in the embedding procedure.The proposed method increased the embedding capacity and reduced the distortions efficiently.Compared with three state-of-the-art reversible watermarking algorithms,the proposed method could well exploit the advantages of block correlation by adaptively selecting blocks of different sizes according to the image characteristics,hence demonstrating excellent performance.Based on this research,the best compromise between embedding performance and complexity can be further studied in the future.

Acknowledgments:This work was supported by the Key Basic Research Plan in Shaanxi Province (Grant No.2017ZDXM-GY-014),and Guangxi Key Laboratory of Manufacturing System &Advanced Manufacturing Technology (Grant No.17-259-05S007).