基于模糊数学模型的土壤肥力质量评价

吴登峰，任震震，戈春华

(1.三峡大学 水利与环境学院，湖北 宜昌 443002； 2.中交一公局第二工程有限公司，江苏 苏州 215010； 3.宜都市农业技术推广中心，湖北 宜都 443300)

0 引 言

土壤是人类赖以生存和发展的物质基础，土壤肥力是土壤的本质属性，其质量的高低直接影响着农作物的生长以及社会等综合效益的发挥[1]。土壤肥力质量评价作为土壤质量评价的基础工作之一，采取科学合理的评价方法，能够准确快速地反映当前的土壤质量和肥力状况，了解土壤的养分迁移和变化规律，进而为农作物科学施肥、合理利用和正确管理提供指导。目前，众多专家学者针对土壤肥力质量评价研究方面取得了丰富的学术成果：戴士祥[2]采用改进层次分析法确定评价指标的权重，建立了基于改进层次分析法的模糊综合评价模型，对安徽省主要水稻土的肥力质量进行了综合评价；吴海燕[3]针对东北黑土区施肥模式，采用主成分分析和聚类分析定量评价了黑土区的土壤肥力，为东北黑土区合理施肥提供指导；林圣玉[4]采取变异系数法求取指标权重，并结合模糊数学隶属度函数模型对鄱阳湖区坡耕地的土壤肥力质量进行了综合评价。目前的研究差异主要集中在对评价指标的权重确定方面和评价的数学分析方法方面，但土壤肥力是由较多复杂因素组合而成，不同的研究方法对其质量评价各有利弊。如层次分析法确权时，受专家的主观思想影响较大，导致各指标的重要程度没有合理的体现；主成分分析法评价土壤肥力质量时，各主成分是按方差大小排列顺序的，在分析问题时，舍弃了一部分方差较小的主成分，造成评价指标的信息没有利用完全等。因此，本研究以利川市东城区坡耕地为研究对象，兼顾主客观权重，采取博弈论对层次分析法和熵权法确定的土壤肥力指标权重进行组合赋权，得出最优组合权重，并结合土壤肥力综合指数法对研究区的土壤肥力进行评价，为研究区精准施肥和农作物规划种植提供理论支撑。

1 材料与方法

1.1 研究区概况

研究区位于湖北省西南部的利川市，区域地理位置大致范围地跨E108°21′-E109°18′，N29°42′-N30°39′之间，属亚热带大陆性季风气候，因境内山峦叠嶂，海拔高度不同，气候差异明显，为典型的山地气候，年降水量1 200～1 400 mm。坡耕地是境内重要的农业生产用地，也是境内土壤侵蚀的重点治理区域。因此，对研究区的坡耕地土壤进行肥力质量评价，以期为境内土地资源的合理开发利用和科学的管理规划提供理论依据。

1.2 土壤样品的采集与分析

在对研究区进行详细踏勘之后，选取研究区具有典型代表性的东城区为研究对象，用GPS定位15个样点，每个样点设立3块样地，每个样地采取S型线路混合多点采样，采集0～20 cm深度的土壤样品，每个样品大约1 kg，装入密封袋中带回实验室分析。土壤样品主要测定有机质、碱解氮、速效磷、速效钾、阳离子交换量(CEC)、pH和黏粒含量共7项土壤养分指标，各属性指标具体的测定方法详见参考文献[5]，每个样品重复测定3次，取平均值。采用章海波[6]等对土壤肥力质量指数的分类法进行分类，其具体的等级见表1。

表1 土壤肥力质量评判标准表

2 土壤肥力质量评价方法的构建

2.1 博弈论组合赋权法

由于土壤属性中的各项指标对土壤肥力的重要程度不尽相同，因此必须针对各项指标的贡献率对其进行合理的赋予权重。为避免人为主观思想和过度依赖数值对赋权的干扰，将层次分析法和熵权法相结合，计算得出最优组合权重。

2.1.1 层次分析法

层次分析法是美国的运筹学家T.L.Saaty提出的一种主观赋权方法，其核心思想是基于专家意见对每一层次的重要程度进行判断，给出定量关系，进而得出合理的权重系数[7]。目前在权重的计算中，因其理论成熟、计算简便而得到广泛的应用。其具体的计算步骤如下：

1) 建立层次模型。基于对问题的内在联系进行分析，明确问题的目标层、准则层和措施层。

2) 构造判断矩阵。根据目标层确定各因素之间相对重要程度，结合标度理论，使用九段标度法，构造两两比较的判断矩阵A。

3) 计算评价指标的权重。按式(1)对判断矩阵的列元素进行归一化处理，进而按式(2)、式(3)计算评价指标的权重和特征向量近似解。

(1)

式中：Zij为归一化后的判断矩阵元素；bij为原始判断矩阵元素。

(2)

(3)

4) 进行一致性检验。依据公式AW=λmaxW，求出最大特征值，并进行一致性检验。

(4)

(5)

(6)

式中：λmax为判断矩阵最大特征值；C.I.为一致性指标；C.R.为一致性比率；R.I.为平均随机一致性指标，本文为7阶判断矩阵，故R.I.=1.32。

2.1.2 熵权法

熵是由申农(C.E.Shannon)引入信息论，在信息论中熵值反映了信息的无序化程度，用以度量信息量的大小[8]。熵权的核心思想是依据各变量的变异程度来明确各指标的权重值，然后通过修正，计算出相对客观的权重。熵权法的计算步骤如下：

1) 假设有n个评价指标m个评价对象组成的评价矩阵A=(aij)m×n，(i=1、2……n；j=1、2……m)即：

(7)

对A进行归一化处理得到：

(8)

(9)

式中：bij为原始指标归一化后的值，对于原始数据进行归一化处理，以消除量纲之间的差异。式(8)为越小越优型公式，式(9)为越大越优型公式。

2) 计算第j项指标的熵值ej，公式如下：

(10)

(11)

2.2 博弈论组合赋权[9]

博弈论主要研究具有斗争或竞争性质现象的数学理论和方法，考虑游戏中个体的预测行为和实际行为，并研究它们的优化策略。在实际决策的过程中，通过博弈协调寻找最大化的利益。在本研究中，就是通过博弈论的思想将主客观权重组合，进而得出最优组合权重，其具体的操作步骤为：

1) 假设使用L种方法计算权重，其中任意的一个权重集合为ωk={ωk1，ωk2，…，ωkn}(k=1，2，…，L)，则L个向量的任意线性组合可表示为：

(12)

式中：ω为最终的权重集的综合权重向量；βk为权重系数，且βk>0。

2) 为了计算出合理的权重值，需要对L个权重集的权重系数βk进行优化计算，最终求得最优组合系数。

(13)

式中：ωg为第g种方式计算得出的权重集合。

3) 依据矩阵微分性质，求解最优组合系数，即将式(13)予以展开，求解线性方程的解。将线性方程的解归一化后代入式(12)中即可得到最优组合权重。

(14)

2.3 指标隶属度及土壤肥力综合指标值的计算

隶属度函数是模糊数学的应用基础，构建正确的隶属度函数是解决模糊数学伦理问题的关键[10]。根据研究区坡耕地的实际情况和测定的土壤肥力属性指标，结合前人的研究成果和经验[11-12]，各项评价指标的隶属度函数转折点取值见表2。常用的隶属度函数分为两类，分别是S型和抛物线形。本研究中的有机质、碱解氮、速效磷、速效钾和CEC为S型隶属度函数，而pH和黏粒为抛物线形隶属度函数，函数表达式如下：

S型隶属函数：

(15)

抛物线隶属函数：

(16)

由此计算得出的各项评价指标的隶属度值，根据其隶属度值大小排序，可以初步判定土壤肥力的优劣。

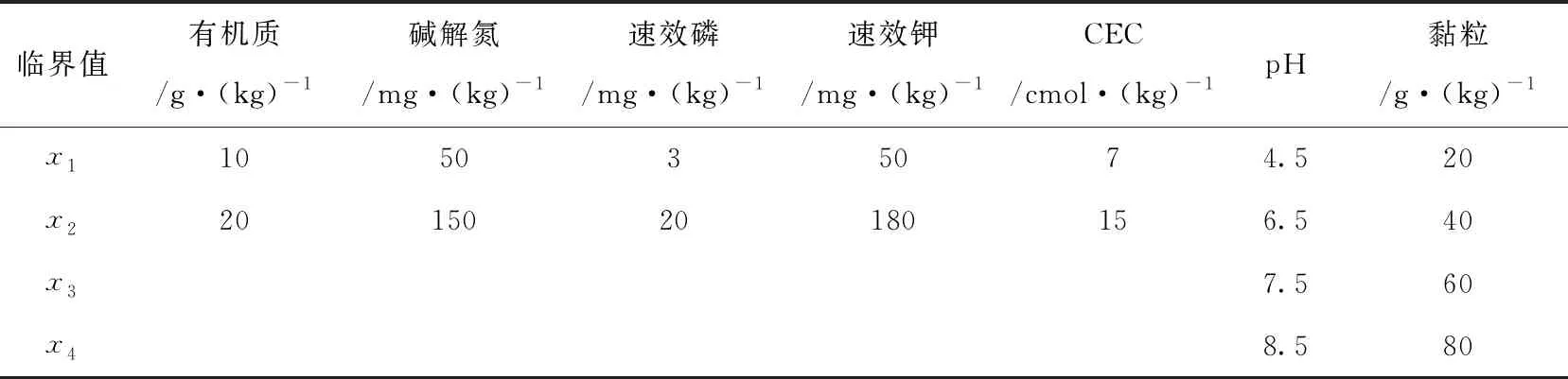
表2 指标隶属函数转折点取值

土壤肥力综合指标值(IFI)能够直观准确地反映土壤的肥力质量信息，广泛应用于土壤肥力的定量研究，其计算公式如下：

IFI=∑WiNi

(17)

式中：IFI为土壤肥力综合指标值；Wi为第i项评价指标的权重值；Ni为第i项评价指标的隶属度值。

3 结果分析

3.1 单因素土壤肥力分析

通过对研究区的样地土壤进行科学的实验分析，选取7项具有典型代表的土壤肥力指标，所测定的原始数据见表3。

根据原始数据表，利用式(15)、式(16)计算出各项指标的隶属度值，进而对研究区土壤进行单因素肥力分析，以期明确研究区土壤肥力质量的限制因素。通过各项指标的隶属度平均值(表4)可看出，黏粒含量的隶属度值最低，CEC和有机质隶属度值排名其次，说明这3项指标是研究区土壤肥力的主要限制因子；碱解氮和速效磷处于中间位置；pH值和速效钾隶属度均值相对较高，表明这两项指标对研究区土壤肥力的贡献最大。农作物生根和生长需要大量的氮磷肥料，但是研究区土壤氮磷含量偏低，且有机质严重不足，因此需要增施大量的氮磷肥料和有机肥以提高研究区土壤质量。

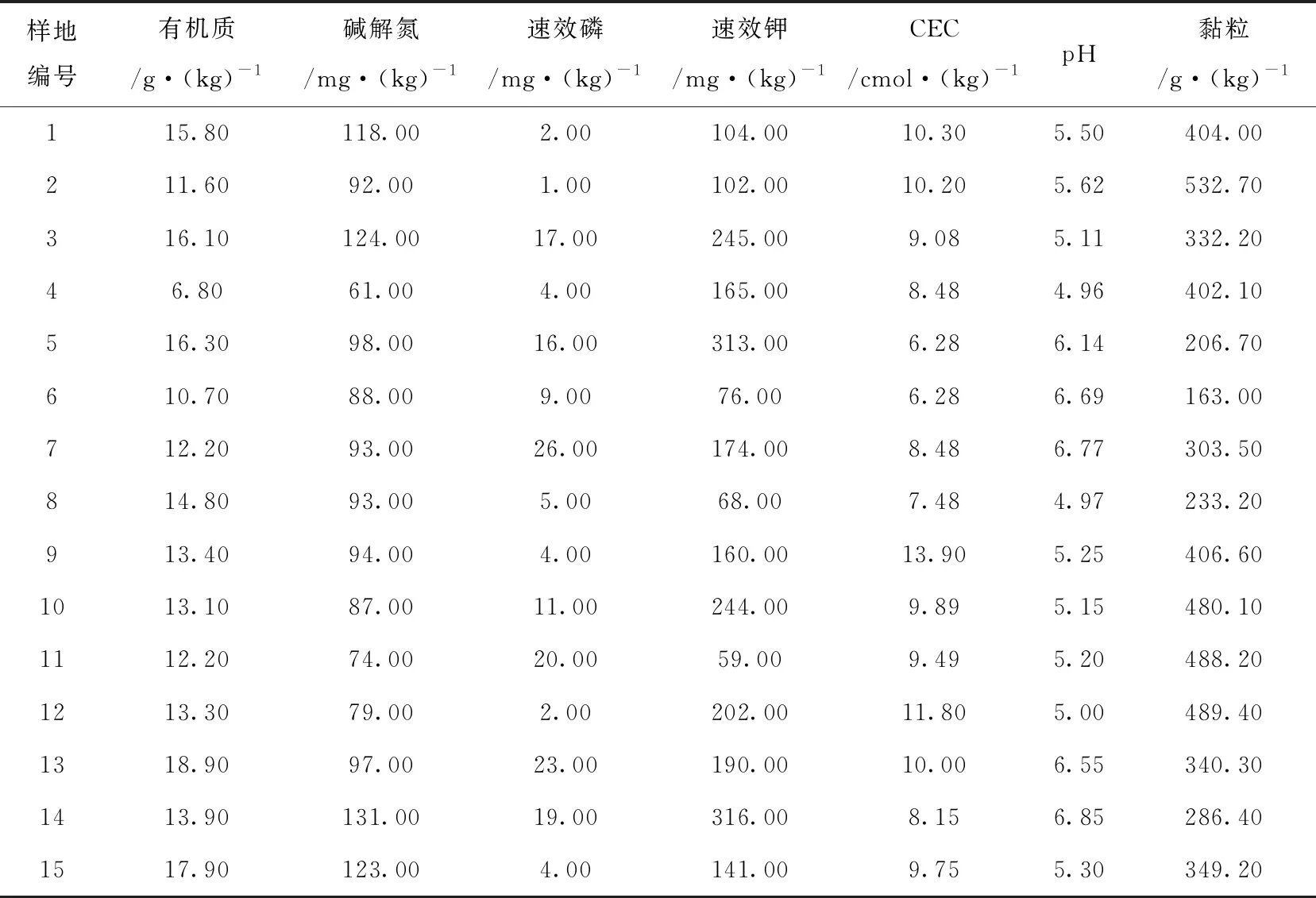
表3 土壤肥力原始数据

表4 土壤肥力指标隶属度平均值

3.2 土壤肥力综合分析

根据前述内容，分别采取层次分析法和熵权法计算评价指标的权重。其中，层次分析法依据所测定土壤属性指标，明确各项指标与土壤肥力质量的内在联系，构建判断矩阵，两两比较，由专家依照九段标度法打分，进而由式(1)-式(3)确定指标权重，并依据式(4)-式(6)进行一致性检验，计算得出判断矩阵最大特征值为7.158，C.I.=0.026，C.R.=0.024<0.1。熵权法由式(7)构建原始判断矩阵，再将判断矩阵依据式(8)、式(9)进行归一化处理，进而得出评价指标的熵值ej=(0.995 5,0.994 1,0.989 4,0.991 4,0.994 1,0.987 4,0.993 3)，利用式(11)可计算出由熵权法求得指标权重值。综合层次分析法和熵权法的权重计算结果，利用式(12)-式(14)计算得出最优组合系数并进行归一化处理，β1=0.323 4,β2=0.676 6，将计算得出的最优组合系数与主客观权重值采取和积法处理，即可得出博弈论最优组合权重值，见表5。

根据原始数据表，利用式(15)、式(16)可以计算出各项指标的隶属度值，见表6。

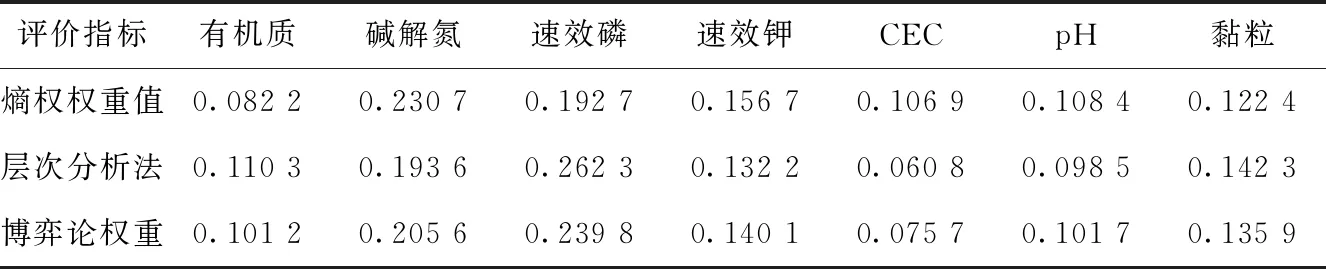
表5 博弈组合权重值

表6 各项指标隶属度值

基于前述博弈论计算所得的最优组合权重(表5)，由于指标隶属度值较多，不便于数据的处理。因此，本文将各项指标的隶属度值与最优权重值采用和积法计算得出一个值，由式(16)可以计算出各样地的土壤肥力综合指数，见表7。

表7 土壤肥力综合指数

以上计算结果显示，研究区土壤肥力综合指标值(IFI)的平均值为0.42，其隶属等级为Ⅲ类，质量评语为中等。结合各样地的肥力隶属等级，大部分样地肥力等级隶属于Ⅲ类和Ⅳ类，较少部分隶属于Ⅱ类，且计算得出的变异系数为37.38%，变异系数值较大，属于高强度变异。究其原因在于研究区属于石漠化地区，土壤肥力较为贫瘠，且研究区广泛种植贝母、天麻等中草药和大白菜、玉米等作物，每种作物所需肥料养分不同，如天麻、贝母等中草药需播种5年后才可收获，肥料用料相对较少；而白菜、玉米等属季节性作物，故肥料使用较多，导致各样地肥力隶属等级变异较大，符合研究区实际情况。

4 结 论

基于利川市东城区土壤样品科学实验分析的基础之上，利用层次分析法和熵权法计算评价指标的权重值，结合博弈论思想，进而得出最优组合权重，运用客观准确的隶属函数模型初步评判研究区的土壤肥力，并结合土壤肥力综合指数综合分析了研究区的土壤肥力质量。最终结果显示，本文的评价模型与研究区的实际情况相一致，且采取博弈论的思想计算指标的最优权重，既避免了人为主观思想的干扰，同时又降低了过>分依赖数据确定权重的不足之处。因此，本文的评价模型可以客观准确地评价土壤肥力质量，该模型思路清晰，在实际应用中具有较强的操作性，可为我国其他地区农作物精准施肥和依据土壤肥力进行规划种植提供参考。